应用量子力学原理对电离辐射屏蔽防护厚度的探讨
兰州军区放射防护监测中心, 甘肃 兰州 730020
在进行放射防护监督监测时, 往往有人问及:到底多厚的铅板才能完全对射线进行防护。在此可应用量子力学原理进行诠释。
量子力学原理认为, 基本粒子(光子、电子、质子等)都具有波粒二项性。量子力学的研究表明, 基本粒子的运动应由薛定谔(Schrodinger)方程描述。下面就应用薛定谔方程对基本粒子通过一定高度方形势垒的穿透率进行讨论。
将一定厚度的物质看作一个势垒, 势垒高度为V0, 势垒宽度为a(图 1)。
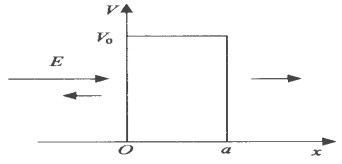
|
图 1 一维方形势垒 |
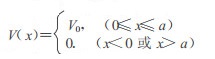
|
在经典力学中, 当入射粒子能量(E)E > V0时, 粒子全部通过; E<V0时, 粒子不能通过。
在量子力学中, 当入射粒子能量(E)E > V0时, 粒子全部通过; E<V0时, 粒子部分通过。
下面讨论量子力学中E<V0时的通过情况。
薛定谔方程在方形势垒中为
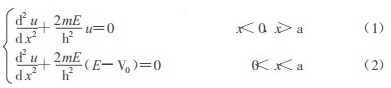
|
其中:u为粒子波函数; m为粒子质量; h为普朗克常数h= 1.055×10-34J·s
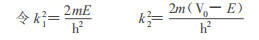
|
(1)(2)式改写为下列(3)(4)式
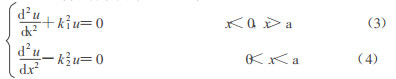
|
解微分方程(3)(4), 得下列波函数

|
(5) |

|
(6) |
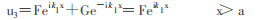
|
(7) |
其中Aeik1x, Ceik2x, Feik1x为入射波; Be-ik1x, De-ik2x, Ge-ik1x为反射波。u3中因为势能为0, 所以Ge-ik1x应为0。
用边界条件求得系数
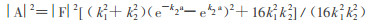
|
(9) |
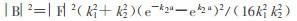
|
(9) |
定义:透射系数T=|F|2/|A|2

|
(10) |
由于普朗克常数h的量级为10-34, 所以k2a »1。则(10)式简化为
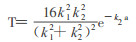
|
(11) |
这里T不可能为0, 说明一定高度和宽度的势垒, 都有透射波存在, 除了当a→∞时, 有T→0。实际这种情况是不可能达到的。
综上分析不难看出, 对于电离辐射防护, 我们不能一味追求低剂量, 而是要以合理的代价取得最佳的防护效果, 这也正是辐射防护最优化所追求的。
参考文献
| [1] |
史斌星. 量子物理[M]. 北京: 清华大学出版社, 1982: 15-83.
|
| [2] |
邓槐春. 放射卫生防护与管理[M]. 广州: 广东高等教育出版社, 1994: 50-79.
|


