20世纪90年代以来, 大体积高效率高纯锗(HPGe)探测器广泛用于环境放射性测量和核事故应急监测等领域。大体积HPGe探测器的优点是探测效率高, 探测下限低, 节省时间。缺点是伴随效率的提高存在的符合相加效应相应的提高到不可忽略的程度, 对放射性核素的定量分析产生不可忽视的影响。为解决这一问题, 我们查阅了国内外放射性核素测量方法的有关资料[1-16], 认为采用蒙特卡罗方法, 模拟放射性核素衰变过程, 理论计算HPGe探测器效率和符合相加修正系数可以解决这一问题, 因此编写了Cool 2000计算机软件程序, 用于计算圆柱体样品的效率, 也可以改变圆柱体高度和半径对点源和面源样品进行效率计算, 计算能量的范围为30 keV~3 MeV。
Cool 2000包含探测器和样品盒参数设置、HPGe探测器效率模拟计算、级联核素的符合相加修正系数计算、探测器死层厚度和冷指尺寸调整计算四部分。为了检验Cool 2000程序的合理性, 笔者制备了不同基质、含不同核素的体源、面源和点源, 在ORTEC ADCOM100+GEM50195 HPGe γ谱仪系统进行了实验效率刻度, 比较实验值与Cool 2000理论计算值, 修改、检验Cool 2000程序。
1 材料与方法 1.1 HPGe探测器效率模拟计算方法HPGe探测器效率模拟计算方法是模拟放射性核素从激发态退激到基态的整个衰变过程, 以模拟跟踪单个光子为基础。模拟时, 首先采用随机数抽取的办法选择(光子在样品中产生点的位置, 对于一圆柱形样品, 其位置均匀分布函数是:
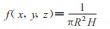
抽样方法是:
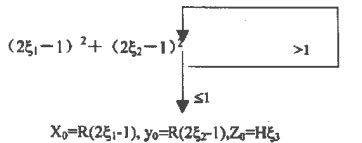
|
其中, ζ1、ζ2、ζ3为三个连续抽取的位置随机数。对于射线的初始出射方向(U0, V0, W0), 如果各向同性, 则其抽样方法是:

|
如果不是各向同性, 在抽取级联衰变射线中后一条射线的出射方向时, 还应考虑与之相邻的前一条射线的初始出射方向和两级联射线之间的角分布问题。本文没有考虑级联衰变射线之间的角分布函数。
抽取到初始γ光子的位置和出射方向后的下一步是对γ光子进行跟踪。对于γ光子在样品及样品容器中的行为, 仅考虑γ光子的最终行为即是否穿出样品, 处理的方法是利用质量衰减系数。设样品的质量衰减系数为μ1, 样品容器的质量衰减系数为μ2, 空气的质量衰减系数为μ3, (光子在其中所经过的路经长度分别为l1和l2, 打在探测器外壳前在空气中所经过的路径长度为l3, 则(光子穿出样品打在外壳上的概率为:
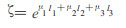
|
当γ光子进入探测器外壳后, 按照γ光子与物质相互作用三种形式的截面进行逐步模拟跟踪。
(1) 光电效应过程。在光电效应过程中, γ光子被原子吸收, 产生光电子, 同时由于内层电子被打出后, 内壳层产生一电子空穴, 核外电子向内跃迁时伴随产生X射线, 方向为各向同性, 位置为γ光子的作用点, 对X射线的模拟与γ射线的方法相同。光电子能量为:
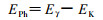
|
其中, EPh、Eγ、EK分别为光电子、γ光子以及介质原子的K壳层核外电子的结合能。光电子与γ入射方向的夹角θ值由下式进行抽样[17]:

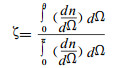
|
光电子方位角φ, 由[0, 2π]区间均匀抽样确定。之后, 即可开始对电子进行跟踪。对γ光子产生的所有次级电子(包括正电子)的跟踪方式如下:电子在物质中的迁移表现为多次散射。在多次散射的过程中, 不断减少能量和改变运动方向。利用能量射程关系, 把电子轨迹细分成若干小的轨迹长度, 使得每一步迁移电子能量缩小一个常数因子K, K值大小与轨迹长度直接相关, 其值按能量射程关系表[18]进行内插得到。
电子由第n次的能量En散射后变成能量为En+1时的散射角余弦[19]为:
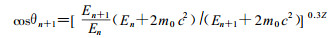
|
式中Z为介质原子序数。方位角φ, 由[0, 2π]区间均匀抽样确定。
(2) 康普顿效应。入射γ光子与物质发生康普顿效应时, γ光子的一部分能量传递给核外电子, 使之成为反冲电子, 而γ光子成为散射光子。散射光子的能量由Klein Nishina公式抽样确定[19]。
散射角的余玄为:
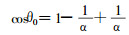
|
式中, α和α'分别为γ光子散射前后的能量(以moc2为单位, m0为电子质量), 方位角φ, 由[0, 2π]区间均匀抽样确定。对于康普顿反冲电子, 其能量为:
反冲电子与入射γ光子的入射方向之间的夹角θe与γ光子的康普顿散射极角θc之间的关系为: 
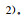
(3) 电子对效应。当γ光子的能量E (大于2m0c2时, 有一定几率发生电子对效应。这时总能量Eγ中将有(Eγ-2m0c2)作为动能由正负电子平均分配。
1.2 符合相加修正系数的计算方法Cool 2000计算机程序是按实际核素的衰变模式, 依次模拟由激发态退激时所发出的γ光子。直到退激到基态为止。每模拟一个原子后, 对模拟结果进行处理, 记录每一种γ光子的能量的总射线数, 以及该能量的光子将其能量全部沉积在探测器灵敏体积中的光子总数, 以便计算出绝对探测效率(无符合的效率)。一个原子核衰变过程中在探测器灵敏体积内所沉积的总能量, 模拟多道谱仪的处理方法:不同的道址对应于不同的能量, 每模拟出一个原子核衰变的全过程中在探测器灵敏体积内所沉积的总能量, 就在对应的道址中加1, 模拟结束后就会得到一个类似多道谱仪所测的γ谱图, 计算出该谱图中感兴趣的峰面积。由于在模拟的过程中, 每一峰值所对应的能量的总模拟的光子数都有记录, 故可用峰面积(测到的能量为E的(光子总数)除以总光子数(源所发出的总光子数), 即可得到考虑符合相加后的绝对探测效率。用没有符合的绝对探测效率除以有符合的绝对探测效率, 即可得到对应能峰的符合相加修正系数。
这样, 使用跟踪单一光子的MC技术, 就可模拟计算整个激发原子核的衰变过程。每个放射性核素衰变过程千差万别, 没有规律可寻, 所以在模拟计算其符合相加过程中只能每个核素逐一编写, 因为工作量较大Cool 2000软件只编写了140La、140Ba、106Ru、106Rh、99Mo、95Zr、95Nb、124Sb、141Ce、131I、132Te等环境放射性监测中所关心的核裂变和活化产生的主要γ放射性核素。
级联放射性核素可以从母核衰变到子核的不同的激发态。我们所测得的γ射线是子核由不同的激发态退激时所发出的。如果在退激过程中(激发态1激发态2激发态3 …基态), 中间激发态的寿命非常短, 小于多道谱仪的分辨时间, 那么, 仪器就会将这几种能量的射线在探测器中所沉积的能量之和当作一种射线的作用结果进行处理, 从而在谱图中产生一个加和峰。在模拟级联核素衰变过程时, 首先根据衰变纲图所提供的母核衰变到子核的不同能级的几率进行归一, 用抽取随机数的办法决定衰变到子核的哪一个能级。抽样方法是:
当随机数ζ<P1时, 子核处于跃迁几率不为零的最高的能基态。
当随机数ζ满足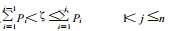
确定子核开始退激所处的能级后, 下一步确定子核从高激发态向哪个能级进行跃迁。如果从一个能级跃迁时有几条可供选择的较低能级, 用类似抽取随机数的方法决定最终的能级。确定初始和结束的能级后, γ射线的能量为两能级能量之差。利用前面所介绍的单γ光子的跟踪方法, 进行跟踪, 计算出该γ光子在HPGe晶体(不包括死层)中所沉积的能量。子核退激到一新的能级后, 用同样的方法决定下一步级联退激所发出的γ光子的能量, 计算出该光子在探测器活性体积中沉积的能量。直到子核退激到基态。
记录下一个子核从激发态退激到基态所有γ光子在探测器活性体积中沉积的能量之和Ei。按能量由小到大的顺序建立一维数组, 利用逐道比较法的原则, 在对应于Ei的数中加1。整个模拟过程中都要记录单个γ光在活性体积中沉积的能量与其全能峰能量相等的射线个数ni, 及所跟踪的对应特征γ射线能量为Ei的总的光子数Ni。模拟结束后, 分析一维数组中所对应各个特征γ射线峰值中的净计数Npi, 利用ni/Npi可计算出每一特征峰所对应的符合相加修正系数。同时用ni/ Ni可计算出没有符合的绝对探测效率。
用蒙特卡罗方法模拟计算HPGe探测器效率时, 需要输入非常准确的HPGe探测器的几何参数, 而一般厂家并不给出探测器冷指、死层厚度等参数, 为了进行MC计算不得不向厂方索要参数, 而厂方所提供的参数往往精度不够, 这就使得计算结果有一定的系统偏差。为了效正这一偏差, Cool 2000根据实验刻度数据, 利用低能(100~400 keV左右)γ射线实验效率调整死层厚度、高能(1 MeV左右)γ射线实验效率调整冷指尺寸来修正这一系统偏差, 以提高计算结果的准确度, 探测器死层厚度和冷指尺寸调整的详细描述见文献[20]。
2 结果为了检验Cool 2000软件计算结果的合理性, 我们用了8种核素(见表 1-3), 选择了国内常用圆柱型样品容器, 制备了基质为水、空气和模拟土壤的体和面标准刻度源, 用ORTEC ADCOM100+GEM50195 HPGeγ谱仪系统做效率刻度, 求出探测器效率和符合相加修正系数, 再将实验得到的效率和符合相加修正系数与Cool 2000计算得到理论值进行比较, 直接检验程序的准确程度; 分别测量点刻度源在距探测器端窗5、10、和25 cm的绝对效率, 并与Cool 2000计算的绝对效率进行比较, 验证程序的可行性。
|
|
表 1 直径72 mm高61mm液体基质体源实测与计算探测效率、符合相加修正系数比较 |
|
|
表 2 直径72 mm高57mm模拟土壤基质体源实测与计算探测效率、符合相加修正系数比较 |
|
|
表 3 直径50 mm空气滤膜基质面源实测与计算探测效率、符合相加修正系数比较 |
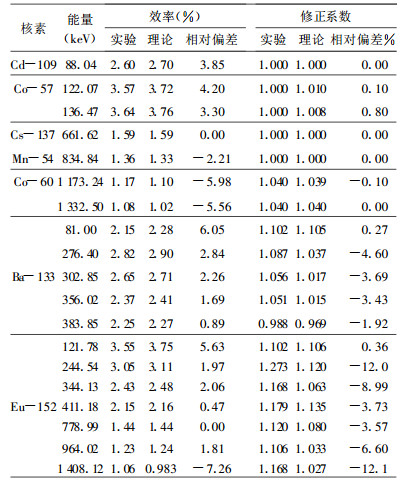
用自制的基质不同(分别为水、空气和土壤)的圆柱型加体标准刻度源在的ORTEC ADCOM+GEM50195 HPGeγ谱仪系统做刻度实验并与计算的效率和符合相加修正系数比较。表 1是用液体(水)基质的体标准刻度源, 样品容器为聚乙烯圆柱盒, 尺寸为直径72 mm高65mm, 样品高度是61 mm, 能量刻度范围是81~1408 keV, 实验与计算的探测效率相对偏差在-7.26%~+6.05%内, 修正系数在-12.1%~+0.8%内。表 2是模拟土壤基质的体标准刻度源的结果。样品容器与上相同, 样品高度为57 mm, 能量刻度范围与表 1相同, 实验与计算的探测效率在-0.86%~+7.22%、修正系数相对偏差在-10.4%~ +1.28%内。表 3是空气采样滤膜面标准刻度源的比较。样品容器为聚乙烯圆柱盒, 尺寸为直径72 mm高30 mm, 样品活性区直径50 mm, 样品厚度为滤膜厚度, 用特制的有机玻璃板压平, 能量刻度范围是121~1 408 keV, 实验与计算的探测效率、符合相加修正系数相对偏差分别在-12.5%~+21.7%、-4.59%~+5.14%内。
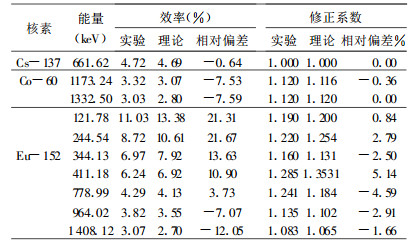
2.2 点源实测绝对探测效率值与理论计算值的比较点源放在特制的有机玻璃支架的托盘内, 托盘中心与探测器同轴, 实测时点源距探测器端窗5、10和25 cm, 能量刻度范围是59.5~ 1408keV, 实验绝对效率值与Cool 2000程序理论计算的绝对效率值比较列于表 4。从表 4可以看出在距离为5、10和25 cm时, 各能量点的实验与计算效率值的相对偏差分别在-8.08%~ +10.6%、-1.35%~+5.60%和-3.04%~1.47%内, 实验与计算的平均相对偏差的绝对值分别为6.00%、2.42%和1.47%。
|
|
表 4 点源距探测器不同距离时计算与实测探测效率的比较 |
(1) 笔者报告的采用蒙特卡罗方法编制的Cool 2000程序, 可用于计算HPGeγ能谱对圆柱型体源、面源和点源的全能峰效率和本文所列部分级联放射性核素的γ射线符合相加修正系数。采用Cool 2000程序计算的ORTEC GEM50195 HPGe探测器对空气(面源)、水和模拟土壤(体源)基质的探测效率和符合相加修正系数与实验值符合的好; 计算的距探测器不同距离处的点源全能峰探测效率与实验值符合较好。
(2) Cool 2000在计算HPGeγ能谱的全能峰探测效率时, 探测器结构、样品基质、样品容器材料、尺寸和与探测器距离等可以调整, 可计算30keV-3MeV能量范围内各能量点的效率值, 确定耗时、耗钱的放射性、特别是环境放射性监测中γ能谱分析的全能峰探测效率和常见级联核素探测效率的符合相加修正系数。目前国内微机技术已经普及, 只要将Cool 2000程序装入微机就能便利的计算和查询HPGeγ能谱的全能峰探测效率和符合相加修正系数, 而只需很少的实验验证。
(致谢: 王思广同志在Cool 2000软件编程上给予作者很大的帮助, 特此鸣谢。)
| [1] |
GB/T 16140-1995, 水中放射性核素的γ能谱分析方法[S].
|
| [2] |
GB/T 16145-1995, 生物样品中放射性核素的γ能谱分析方法[S].
|
| [3] |
GB 11743-89, 土壤中放射性核素的γ能谱分析方法[S].
|
| [4] |
GB 11713-89, 用半导体γ谱仪分析低比活度γ放射性样品的标准方法[S].
|
| [5] |
郝润龙, 谭金波.JJG578-94锗γ谱仪体源活度测量装置检定规程[S]。 |
| [6] |
谭金波. 锗γ能谱测量中的符合相加修正[J]. 辐射防护, 1989, 9(2): 101. |
| [7] |
何宗慧. 近距离测量时Ge (Li)探测器的峰效率刻度和符合相加修正[J]. 辐射防护, 1986, 6(6): 431. |
| [8] |
Debertin K.and Schotzig U.Coincidence summing corrections in Ge (Li)-spectrometry at low source to detector distances[J].Nuclear Instruments and Methods.1979158, 471.
|
| [9] |
Ashrafi S, Likar A, Vidmar T. Precise modeling of a coaxial HPGe detector[J]. Nuclear Instruments and Methods, 1999, 438: 421. DOI:10.1016/S0168-9002(99)00862-1 |
| [10] |
Gerhard Haase, David Tait, Arnold Wiechen. Application of a new Monte Carlo method for determination of summation and self -attenuation corrections in gamma spectrometry[J]. Nuclear Instruments and M ethods, 1993, 336: 206. DOI:10.1016/0168-9002(93)91099-9 |
| [11] |
Korun M, Likar A, Vidmar T. Monte-Carlo calculation of the spatial dependence of the coaxial HPGe detector efficiency for point sources[J]. Nuclear Instruments and Methods, 1997, 390: 203. DOI:10.1016/S0168-9002(97)00378-1 |
| [12] |
Marc Decombaz, Jean Jacques Gostely, Jean Pascal Laedermann. Coincedence summing corrections for extended sources in gamma-ray spectrometry using Monte Carlo simulation[J]. Nuclear Instruments and Methods, 1992, 312: 152. DOI:10.1016/0168-9002(92)90146-U |
| [13] |
Arnold D, Wershofen H. Specific calibration problems for gamma spectrometric measurements of low-level radioactivity in environmental samples, Methods and applications of low-level radio avtivity measuements[J]. Proceeding, 1997, 170: 1139-142. |
| [14] |
Sima O. Application of Monte Carlo calculations to gamm-spectrometric measurments of environmeental samples[J]. Applied Radiation and Isotopes, 1996, 47(9-10): 919-923. DOI:10.1016/S0969-8043(96)00087-5 |
| [15] |
Sima O, Arnold D. Self-attenuation and coincidence-summing corrections caculated by Monte Carlo simulations for gamma- spectrometric measurements with well-type germanium detectors[J]. Applied Radiation and Isotopes, 1996, 47(9-10): 889-893. DOI:10.1016/S0969-8043(96)00082-6 |
| [16] |
Semkow T M, Mehmood G, Parekh P P. Coincidence summing in gamma-ray sepectroscopy[J]. Bulletin of the American Physical Society, 1993, 38(9): 1849. |
| [17] |
L al B, lyengar K V K. Monte Carlo calculations of Gamma ray response characteristics of cylindrical Ge (Li) detectors[J]. Nuclear Instruments and Methods, 1992, 19: 19. |
| [18] |
Pages L, Bertel E, Joffre H. Energy loss range and bremsstrahlung yield 10keV to 100 MeV electrons in various elements and compounds[J]. Atomic data, 1972, 4(1-4). |
| [19] |
肖雪夫. 就地HPGe (谱仪校准系数的蒙特卡罗计算[J]. 辐射防护, 1999, 19(1): 43. |
| [20] |
徐翠华, 王思广, 周强, 等. 蒙特卡罗方法调整探测器死层厚度和冷指尺寸的研究[J]. 中国辐射卫生, 2002, 12(4): 203-204. |