皮肤位于人体体表, 在受到弱贯穿辐射照射时, 人体皮肤会受到远高于深层器官或组织剂量的照射, 而可能受到损伤, 它是较常遇到的放射性疾病, 其中, β射线皮肤损伤所占的比例较大。在核爆炸, 反应堆事故, β放射源和核素的应用中都可能造成β射线皮肤损伤, 因此, 无论从核事故应急准备和平时的放射防护, 以及放射性疾病诊治等考虑, 都需要对β射线所致皮肤损伤的剂量估算原则和方法进行研究和规范, 以便制定相应的标准。β射线属于弱贯穿辐射, 较强贯穿辐射(X、γ射线和中子)的剂量估算难度更大, 并具有特殊性。由于β射线易于被物质吸收和散射, 即使在不太厚的皮肤层中, 剂量变化也很大。因此难于准确的对皮肤剂量进行测量和估算。本研究的目的之一在于给出较合理方法及较可靠的数据资料, 使皮肤剂量估算规范化, 以便使皮肤剂量的估算有可比性和相对较好的可靠性, 并力图给出简便适用的β射线皮肤剂量估算方法。
1 β射线皮肤剂量估算的一般原则根据ICRP 59号出版物[1]和ICRU 56号报告[2], 认为引起随机性效应(皮肤癌)产生的靶细胞的位置是在皮肤深度为0.02~ 0.1 mm处的表皮的基底层。ICRP 26号出版物[3]的观点也认为皮肤的基底层是具有最大危险度的细胞位置。ICRP 26号和60号出版物都建议基底层的深度范围是从0.05 ~ 0.1 mm, 并认为0.07 mm是基底层深度的一个合理的平均。有关文献[1, 2]还指出:为了反映皮肤的急性和慢性确定性效应, 给定皮肤剂量的深度大约应在0.3 ~ 0.5 mm。而对象真皮坏死这样的确定性效应, 主要是由于皮肤深部真皮血管的损伤, 靶深度约在1~ 1.5 mm。综上考虑, 一般可用受照皮肤0.07 mm深处的吸收剂量来评价皮肤产生的随机性效应, 用受照皮肤0.3~ 0.5 mm深处的吸收剂量来评价皮肤产生的确定性效应。当可能产生射线所致真皮坏死这样的确定性效应时, 还应估算受照皮肤1~ 1.5 mm深处的吸收剂量。
由于皮肤受照常常是不均匀的, 无论从剂量监测和剂量评估来考虑, 都需要指定一个适当的面积, 在该面积上进行剂量平均。有关文献[5, 6]建议采用1 cm2的面积, 这样的面积也与日常监测用的热释光片的面积大小相近。因此, 对不均匀照射的皮肤, 一般可用以所求剂量点为中心, 周围1 cm2面积上的平均皮肤吸收剂量来代表该处的皮肤吸收剂量。对较大面积皮肤受到不均匀照射, 必要时, 可给出受照面积上的皮肤吸收剂量分布图。ICRP 59号出版物等有关文献还指出:确定性效应的发生受照射面积、辐射能量、照射的均匀度、剂量率和照射间隔时间等的影响, 因此对皮肤剂量进行评估时, 除给出皮肤剂量外, 还应指明β核素的种类、β射线的最大能量和平均能量、剂量率、受照面积的大小、分次照射的次数和照射间隔的时间等。
为了能够可靠的估算β射线皮肤剂量, 可在可能受到照射的部位佩戴组织等效β射线个人剂量计(例如, 薄的LiF(Mg, Cu, P)热释光个人剂量计)监测。为了同时测得表皮、浅的和深的真皮三个深度的皮肤剂量, 可使用由三个能测得相应深度皮肤剂量的薄的组织等效β剂量元件, 叠合成的组合式个人剂量计监测。对于手部皮肤的剂量监测, 可在手指上佩戴β射线指环剂量计。
2 皮肤剂量的估算方法 2.1 使用经验公式对β射线皮肤剂量率的估算 2.1.1 点源如果点源周围的介质是均匀的, 在距离点源r处的吸收剂量率为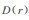

|
(1) |
式中: D(r)—距离点源r处的吸收剂量率, Gy·h-1; r—距离点源的质量距离, g·cm-2; A—β点源的放射性活度, Bq.
式(1)中其他系数分别依据下述各式计算:
归一化系数K(Gy·h-1.Bq-1), 依据式(2)计算。
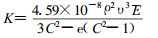
|
(2) |
式中: ρ—吸收介质的密度, g·cm-3, 对皮肤ρ的平均值为1.1g·cm-3; е—自然对数的底为, 2.718; E—β粒子的平均能量, MeV; 参数C和υ分别依据(3)~ (5)式计算。
对皮肤
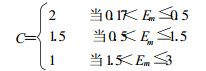
|
(3) |

|
(4) |
式(4)中

|
(5) |
Εm—β粒子的最大能量, MeV; E*—禁戒跃迁的β粒子的平均能量, MeV。
β放射性核素能谱的最大能量Εm和平均能量E, 可从文献[2, 7]中查到。
2.1.2 圆形平面源在圆形平面源的中心上方z(g·cm-2)处的剂量率

|
(6) |
式中; 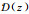
在无限平面源上方z(g·cm-2)处的剂量率
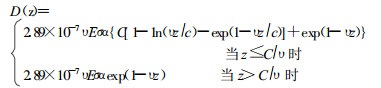
|
(7) |
式中的符号意义同第2.1.1节和2.1.2节。如果圆形平面源的半径a超过β射线在介质中的最大射程, 则可利用(7)式, 计算z处的剂量率。
2.2 使用有关数据对一些照射条件下的皮肤剂量率的估算 2.2.1 皮肤β污染所致皮肤剂量率
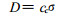
|
(8) |
式中: 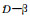
在ICRU有关报告[2]中给出污染面积分别为1 cm2和100 cm2圆时一些常用核素单位污染面密度所致皮肤深度0.07 mm和0.4 mm处的β射线剂量率, 可参考应用。
2.2.2 垂直入射β射线所致皮肤剂量率

|
(9) |
式中: 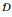
在ICRU有关报告[2]中给出垂直从空气入射的宽束β射线在水模中0.07 mm和0.4 mm深处单位注量所致吸收剂量, 可近似用于该种条件下的皮肤剂量率估算。
2.3 β射线皮肤累积剂量的估算考虑到放射性核素不断衰变的因素, 当已知由上述第2.1节和2.2节中求得的各种β射线受照条件下的皮肤剂量率时, 可依据下述方法估算累积皮肤剂量
2.3.1 皮肤受照终结时皮肤剂量率
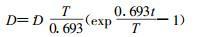
|
(10) |
式中: D—皮肤剂量, Gy; 
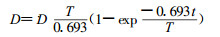
|
(11) |
式中符号意义同式(10)
2.3.3 皮肤受照中间某一时刻皮肤剂量率可分别依据式(10)和式(11)计算皮肤在整个受照期间的剂量。
2.3.4 其他因素影响时皮肤剂量率对非单纯由于核素的衰变引起β源活度的变化时, 由某时刻的皮肤剂量率推算皮肤剂量的问题还应考虑其他因素对β源活度变化的影响(例如, 在核反应堆事故中, 释放到空气中的各类核素的浓度和沉积在地表上的各类核素的面密度受风向、风速与降水强度等气象因素影响很大时, 应在这类剂量估算中考虑这些因素的影响)。
3 讨论由于在实际的剂量估算中, β核素的种类、射线能量、分布情况和受照的几何条件等都很复杂, 本研究不可能对各种受照情况都给出具体的估算方法, 只能就β射线剂量估算的一般原则和方法进行必要的研究, 给出一些典型条件下的剂量估算方法。对于本研究未包括的受照条件下的β射线皮肤剂量估算问题, 可参照本研究, 通过实际监测皮肤剂量或使用剂量计和人体体模(包括全身、躯干、肢体等体模)模拟测量皮肤剂量或依据有关研究结果加以解决。
文中公式(1)~ (7)严格来讲, 应该用于无限介质中, 而对实际皮肤剂量的估算往往是针对靠近组织-空气的边界处, 其可能引入约30%的误差。对于一些实际受照情况, 这样的准确度是足够的。如果需要进一步提高准确度, 可使用β射线反散射系数进行修正, 具体可参考有关文献[2]中的相关内容。公式(9)对实际β射线而言, 只能近似的应用。因为由于空气的散射, 完全平行的β射线束是不存在的。
| [1] |
ICRP Publication 59[M].1991.
|
| [2] |
ICRU Report 56[M].1997.
|
| [3] |
ICRP Publication 26[M]. 1977.
|
| [4] |
ICRP Publication 60[M]. 1990.
|
| [5] |
Dennis JA. Skin dosimetry-radiological protection aspects of skin dosimetry[J]. Radiat.Prot. Dosim, 1991, 39(1/3): 205-206. |
| [6] |
Charles MW. General consideration of the choice of dose limits averaging areas and weighting fact for the skin in the light of revised skin cancer risk figures and experimental data on non-stochas effects[J]. Int.J. Radiat.Biol, 1990, 57(4): 841-850. DOI:10.1080/09553009014550971 |
| [7] |
ICRP Publication 38[M]. 1983.
|


