在事故剂量学和辐射流行病学研究中, 剂量重建占据着十分关键的位置。在这些研究或辐射防护评价中大多缺乏个人剂量资料, 而需要用适宜方法进行剂量重建。在剂量重建的剂量测定方法中, 利用事故现场材料的前剂量技术[1, 2]是一种很重要的方法。这种技术是将先前受到过照射的辐射事故现场样品(砖、瓦等), 进行机械和化学处理, 提取出样品中的石英, 通过适当温度热激活后, 其110 ℃TL峰值的灵敏度有很大提高, 提高的程度与先前受到的剂量(前剂量)成正比, 并利用此特性, 进行剂量重建。人们利用这一技术已对日本的广岛、长崎[3]、美国内华达核试验落下灰[4]和切尔诺贝利事故[5]进行了剂量重建。
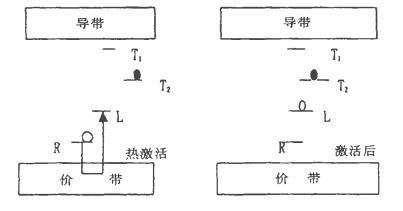
1 前剂量技术基本原理所谓前剂量效应[6, 7]是指石英受电离辐射后, 能以某种稳定的形式记录下受照射剂量的大小。当通过适当的温度激活后, 测量其110℃热释光峰的响应来确定受照射剂量的大小。先前受照射的石英样品通过热激活使其110℃峰的响应值有很大提高, 且提高的程度正比于先前受照射的剂量的大小。可用图 1所示的模型来解释。
|
图 1 石英前剂量敏化模型 |
在此模型中假设发光中心有两种状态。一种是激活状态, 在此状态下发光中心可以接受电子并发光。另一种状态是退激活状态, 在此状态下发光中心不能接受电子也不能发光。激活状态可以以通过失去空穴而变为退激活状态。在图中L是发光中心, R是储存中心。它们均为空穴陷阱。T1和T2是电子陷阱。辐照期间空穴被优先捕获在储存中心R上。电子分别被捕获在T1和T2电子陷阱上。由于T1的深度很浅, 在常温下陷阱的电子就可以获得足够的能量逃逸出陷阱, 因此电子保持在此陷阱的时间仅数小时。T2陷阱是很深的电子陷阱, 在常温下陷阱中的电子很难逃逸出陷阱, 因而电子在T2陷阱稳定的。在室温下R中心上的空穴是稳定的, 在高温时空穴将被驱赶出来。在热激活期间一旦空穴被驱赶出来就被L中心捕获。这样L中心的空穴数目超过了最初所存在的数目。在加热时可使T2中的电子向T1中迁移, 并使得从T1中跳出的电子被L中心捕获的几率增大。因此, 当我们进行110℃热释光峰的测量时其热释光响应也相应的增加。
利用前剂量技术进行剂量重建的回顾性剂量测定时, 现场样品(如砖、瓦)中的总的吸收剂量包含两种成分: (1)天然本底剂量; (2)来源于放射事故的剂量。可表示为:
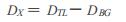
|
式中DX为事故剂量; DTL为利用前剂量热释光技术测得的总剂量; DBG为天然本底剂量。
2 样品处理方法并非所有的矿物晶体都具有前剂量效应, 至今只发现石英的110 ℃峰具有明显的前剂量效应。故提取事故现场建筑材料中的石英是本实验的关键, 本实验以红砖为样品。样品处理主要包括机械和化学处理, 图 2为样品处理的基本过程。
|
图 2 砖块样品处理的基本过程 |
去除样品表面3 mm厚的表层, 经粉碎的砖块颗粒利用标准筛筛取80目以下的颗粒, 用XZY-1100 *500摇床将矿砂和粘土分离, 然后利用WCF-1-63自动磁分离仪对样品进行磁分离弃去磁性颗粒, 经鉴定非电磁性颗粒80 %以上为石英颗粒, 因石英颗粒外有粘土包被, 故呈红色。
2.2 样品的化学处理红砖样品经过机械处理后, 还必须进行化学处理, 在参考国外文献的基础上, 结合本实验室条件, 筛选出了最佳化学处理方法, 如下:
(1)用蒸馏水清洗至水清为止;
(2)丙酮中清洗10 min, 然后再用蒸馏水清洗2 ~ 3次;
(3) 40 %HF处理:将样品置于一塑料杯中, 加入40 %HF, 处理1 h, 其间可用一塑料棒搅拌以加快粘土的分离, 直至样品基本呈白色, 用蒸馏水清洗, 如果样品仍呈少许红色, 可再加少许40 %HF, 但此时力度要轻, 至样品呈无色, 再用蒸馏水清洗;
(4) 样品经上述步骤处理后, 在50 ℃的AlCl3饱和溶液中处理15 min; 样品在浓HCl中处理30 min, 再蒸馏水清洗, 80℃干燥。筛取100 ~ 200目石英颗粒备测定。
3 最佳实验条件的选择利用石英前剂量技术进行剂量测定时受很多因素的影响[8], 主要有激活温度、激活时间等。激活温度是否合适, 对前剂量估算来讲是一个重要的影响因素, 在热激活处理时, 对石英110℃热释光峰的响应值与激活温度的关系作图, 就可得到石英的热激活曲线。
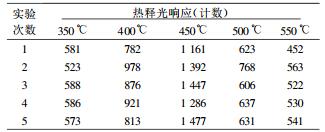
表 1给出了几种不同激活温度下由砖块样品提取的石英的热释光响应结果。可以看出, 在温度低于450 ℃时, 石英颗粒热释光峰的灵敏度随激活温度的升高而增加, 当温度超过450 ℃时, 随温度增高其热释光灵敏度逐渐降低, 故选择最佳激活温度为450℃。
|
|
表 1 样品不同激活温度的热释光响应(相对值) |
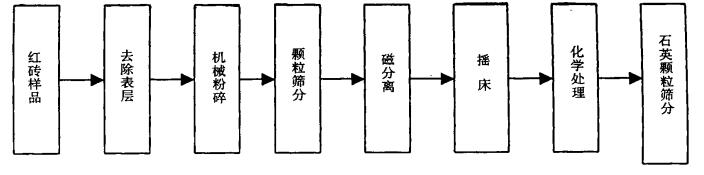
以往的研究中发现, 石英的前剂量热释光响应的高低不但同激活温度有关, 而且还和激活的时间有关, 在激活温度为450 ℃, 其他条件不变的情况下, 分别用10、20、30、40、50、60 min的激活时间进行激活, 测量其110℃热释光响应结果如图 3。从图 3可以看出, 激活时间为10、20 min时, 石英的热释光响应较低, 30 min, 响应最高, 时间超过30 min略有下降, 故选择30 min为最佳激活时间。
|
图 3 不同激活时间热释光响应曲线 |
此外, 利用前剂量技术进行剂量测定时应注意, 热激活后石英110℃热释光信号衰退比较迅速, 所以激活后前剂量测定时应在照射检验剂量后尽快测量110℃的热释光响应, 以减少因衰退引起的误差。
4 剂量刻度方法根据样品中石英前剂量的线性关系, 还可以利用最小二乘法原理做热释光响应值与剂量的直线回归, 建立剂量刻度曲线求得事故受照剂量。基本思想为: ①选取受照样品和对照(本底)样品; ②取部分受照样品, 分别给予不同剂量的附加刻度剂量(βi)照射; ③样品处理, 进行前剂量热释光测量; ④求各测量值与对照(本底)的前剂量热释光响应值之差; ⑤求附加刻度剂量βi热释光响应, βi热释光响应=附加了刻度剂量的受照样品热释光响应值-受照样品热释光响应值; (i =0, 1, 2, 3, 4 ……) ⑥以附加刻度剂量βi为自变量, βi热释光响应为因变量, 建立直线回归曲线, 求得其斜率K, 此斜率即相当于单位剂量的石英样品的前剂量热释光响应值; ⑦求出事故照射的样品与对照样品的前剂量热释光响应值之差, 其与斜率K的比值, 即为事故受照剂量。
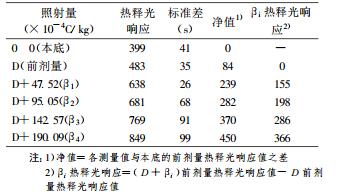
5 模拟照射的剂量估算以砖块作为样品, 通过对样品的机械处理和化学处理, 将石英从中提取出来, 模拟事故照射, 利用刻度剂量法进行了事故照射的剂量估算, 结果如表 2。
|
|
表 2 样品热释光响应表 |
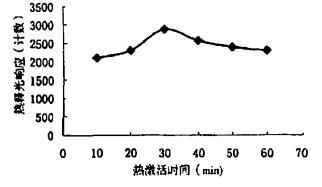
对表 2中刻度剂量βi的前剂量热释光响应与βi(D的附加刻度剂量为0)做直线相关与回归分析, 根据表 1, 可求得刻度剂量βi前剂量热释光响应与βi直线回归方程为y =1.816 x, 斜率为1.816, 即单位照射量的响应值K为1.816, 则估算的前剂量为: 
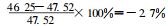
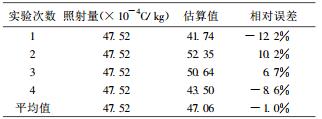
在另外一次利用剂量刻度曲线进行的剂量估算中, 实际照射量仍为47.52 ×10-4C/kg, 估算的剂量为47.54 ×10-4C/ kg, 相对误差为0.1 %, 此外, 我们把此次估算过程中每个附加刻度剂量求出的估算值求出, 当作一次独立的利用前剂量[8]公式估算剂量的实验, 并求其平均值, 结果见表 3。
|
|
表 3 每份样品求得的估算值 |
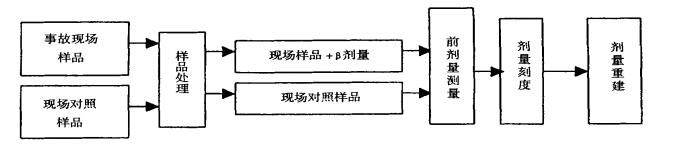
在这次剂量估算中, 可以看出, 独立的一次实验所求的的结果的相对误差大于利用剂量刻度曲线的方法, 并且利用剂量刻度曲线进行的估算结果要比求平均值的方法要准确一些。根据这几次估算结果, 我们认为应该选择刻度曲线法。其基本过程可用图 4表示。
|
图 4 前剂量技术剂量重建流程图 |
本研究以可在事故现场获得的砖块为样品, 利用前剂量热释光技术初步建立了一种辐射事故剂量重建的剂量测定方法, 具有取材方便、方法简单、快速等优点。可为估算无剂量监测资料时的事故剂量及流行病学研究中的剂量重建提供必要的剂量学的资料。在前剂量技术应用时, 一些重要影响因素如激活温度、激活时间等要给予重视并严格控制以便提高测量精度。
| [1] |
Dai G.F., Yuan S., Chang H., et al. The study on pre-dose ef-fe ct of quartz[J]. Radiat.Prot.Dosim, 1998, 77(1-2): 51-53. |
| [2] |
Bailiff I.K.The pre-dose technique[M].Radia Meas, 1994, 23, (2 / 3) : 471-479.
|
| [3] |
Nagatomo T, Hoshi M, Ichikawa Y.Thermoluminescence dosime-try of the Hiroshima atomic-bomb gamma rays between 1.59 km and 1.63 km from the hypocenter[J].Health Phys, 1995, Oct; 69 (4) : 556-9.
|
| [4] |
Haskell H., Bailif I.K, Kenner G.H., et al. Thermoluminescence measurements of Gamma-ray doses atributable to fallout from the revada test site using building bricks as natural dosimeters[J]. Health Phy, 66(4): 380-391; 194. |
| [5] |
Bailiff I.K. The use of ceramics for retrospective dosimetry in the Chernobyl exclusion zone[J]. Radia Meas, 1995, 24(4): 507-511. DOI:10.1016/1350-4487(95)00020-F |
| [6] |
McKeever S.W.S., chen C.Y., Halliburton L.E. Point defects and the pre-dose effect in natural quartz[J]. Nucl Tracks, 1985, 10: 489-495. |
| [7] |
Yang X.H, McKeever S.W.S. The pre-dose effect in crys-talline quartz[J]. J.Phys.D : Appl Phys, 1990, 23: 237-244. DOI:10.1088/0022-3727/23/2/017 |
| [8] |
戴光复, 苑淑渝, 常贺新, 等. 石英前剂量热释光方法研究[J]. 中国辐射卫生, 1996, 5(1): 50-52. |