当前,放射治疗已成为治疗肿瘤的主要手段之一,而对治疗方案的进行评估则采用肿瘤控制概率(Tumor Control Prcbabiliy TCP)这是由于TCP方法除了考虑了辐射剂量的影响外,还包含了生物方面的影响因素,如细胞的辐射敏感性、复制增殖等,比较全面地反映了治疗方案所达到的效果。自MunroTR等人[1]提出TCP的基本思想以来,经过许多学者的努力,另外一些影响治疗效果的因素被考虑进来,所提出的TCP计算模型也越来越完善[2]。但同时,由于技术水平的限制,在实际工作中不可能对每个病人的生物学参数进行实测。因此,如果所采用的数据不准确将会导致最后计算结果的不准确,从而造成对治疗方案评估的不准确。为了探讨TCP计算模型中各个参数的取值变化对计算结果的影响,下面将采用所提出的TCP计算模型对此进行研究。
1 材料和方法 1.1 肿瘤模型为了简便地勾勒出各参数的变化对TCP计算结果的影响,我们采用对称的球型肿瘤模型,假设治疗方式为内辐射治疗,核素为32P且在球型肿瘤内均匀分布。
1.2 计算模型[3]
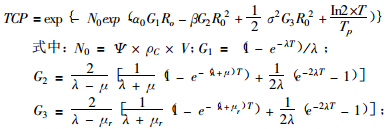
|
(1) |
其中,Ψ是所需杀灭的具有增殖能力的克隆源性细胞在肿瘤细胞中的比例;ρC是细胞密度,cm-3; V是肿瘤体积,cm3; λ是核素的衰变常数,d-1; T是治疗时间,d; α0 (α是平均值)、β是辐射敏感性,单位分别为:Gy-1和Gy-2; σ是辐射敏感性α的标准差,Gy-1; R0是初始时刻的剂量率,Gy/s; μr是再敏感化速率(μr =ln2/Tr,Tr是再敏感化时间常数), d-1; μ是DNA单链损伤修复速率(μ=ln2/Tμ,Tμ是DNA单链损伤修复的半值修复期), d-1; Tp是克隆源性细胞的潜在倍增时间,d。均匀分布的球源内外、距边缘距离X处任意点的初始剂量率R0可由(2)式求得4]:
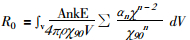
|
(2) |
其中, A是球体内的放射性活度(下文所指活度均为放射性活度), dis/s; n是每次衰变所放出的粒子数, dis-1; k=1.602×10-10g·Gy/Mev; E为所发出粒子的平均能量, Mev; X90是点源时90%能量被吸收时距源的距离, cm; ρ是介质密度, g/cm3; an是多项式模拟系数; V是球体体积, cm3。
1.3 假设的肿瘤生物学参数由于肿瘤类型的差异及个体差异,其生物学参数在不同病人及不同种瘤间变化很大,为方便计算,根据资料[5~7]我们选取了一组假设的肿瘤生物学参数,取值为:α0=0.3Gy-1, α/β=10 Gy, σ=0.03 Gy-1, Tμ=0.04 d, Tr=0.25 d, Ψ=0.1, ρc=108/cm3, Tp=5d, 另外假设所用治疗活度A为3.7×107Bq。
利用上述的一组假设的参数取值及球型肿瘤模型,我们假定其中某个参数的取值发生变化,选取几个不同的值,而此时其他所有参数的取值均不变,用VB6.0将上述TCP计算模型编制成程序进行计算,然后在同一坐标中画出该参数取不同值(所有参数取值变化幅度类似)时TCP与肿瘤半径变化之间的关系曲线进行分析。
2 结果和讨论当某一参数取不同值、而其他参数均采用上述假设参考值时,根据计算结果所画出的曲线如图 1至图 6所示。则:
|
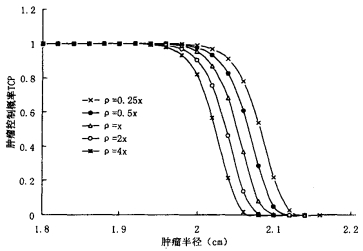
图 1 不同细胞密度时的TCP与肿瘤半径关系曲线(其中X=108个/cm3) |
|
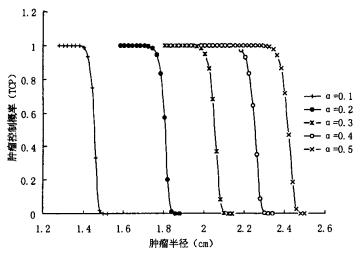
图 2 不同放射敏感性α时的曲线 |
|
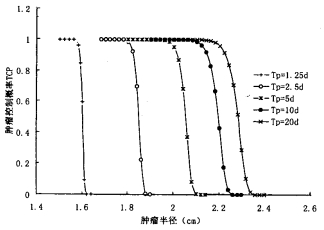
图 3 不同细胞倍增时间Tp时的曲线 |
|
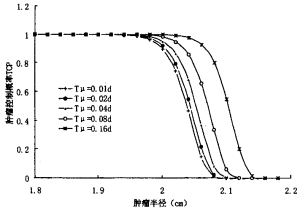
图 4 不同半值修复期Tμ时的曲线 |
|
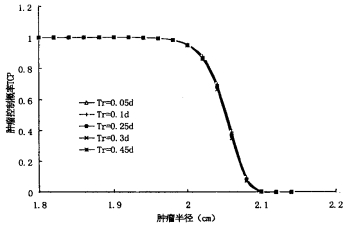
图 5 不同再敏感化时间常数Tr时的曲线 |
|
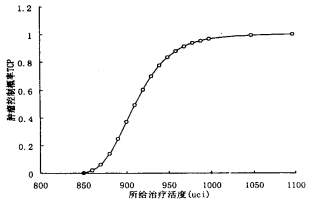
图 6 32P均匀分布球源、肿瘤半径为2cm时肿瘤控制概率与所给治疗活度的关系曲线 |
(1)由图 1至图 5可知,一定治疗活度只能治疗一定半径以内的肿瘤,否则效果会很不理想,也就是说要想获得较好的TCP,必须注意肿瘤体积的影响。
(2)由图 6可知,对于一定半径大小的肿瘤来说,所给予的治疗活度必须大于一个临界值,也就是说所给予肿瘤的吸收剂量必须大于一个临界值,否则治疗会收效甚微,但太大的吸收剂量并不能提高治疗效果,所以也没有必要盲目加大治疗活度。
(3) 由上可知,肿瘤的吸收剂量和体积对TCP产生的影响较大,但由于在制定治疗方案时,肿瘤体积可以通过CT等设备确定,吸收剂量可据核素的分布情况通过计算准确获得,所以实际应用中只要条件具备,这两个参数不会因为取值不准对TCP计算结果产生偏差影响。真正会对TCP计算结果产生的偏差影响的是由于不能实测造成的取值不准确的肿瘤生物学参数,在图 1至图 5中,比较各参数取值变化幅度相同时所导致的TCP与肿瘤半径关系曲线的变化幅度可知,对于给定治疗活度的肿瘤来讲,辐射敏感性α及克隆源性细胞的潜在倍增时间Tp的变化对TCP计算结果的影响要较细胞密度ρc、DNA单链断裂的半值修复期Tp及再敏感化时间常数的变化对TCP计算结果影响大得多,其中尤其以α的变化对TCP结果影响为大。当然,由于目前可能还存在一些目前未考虑进TCP计算模型中的因素,如治疗过程中肿瘤的缩小可能会导致辐射敏感性发生变化[8]等可能影响TCP结果的因素,因此还需要进一步研宄更加完善的TCP计算模型,找出可能存在的其他对计算结果影响较大的因素。
由于每个病人肿瘤的生物学参数都存在差异,而目前的技术条件又不可能在对每个病人制定治疗计划前对该病人的生物学参数进行实测,所以在采用TCP对治疗计划进行评估时,不可避免地要采用一些实验获得的数据。如果所采用的生物学参数值与病人的实际值差距较大,将会导致评估的失误,所以,计算时所采用的对计算结果影响较大的几个参数取值应当力图准确一些。当然,准确了解该病人肿瘤的生物学参数最好,这也正是目前所倡导的治疗个体化的努力方向。
| [1] |
Munro TR, Gilbert CW. The relation between tumour lethal doses and the radiosensitivity of tumour cells[J]. Br J Radiol, 1961, 34: 246-251. DOI:10.1259/0007-1285-34-400-246 |
| [2] |
鞠永健, 孙福印, 苑淑渝. 放射治疗中肿瘤控制概率的计算方法[J]. 国外医学放射医学核医学分册, 2000, 24: 138-140. |
| [3] |
鞠永健, 孙福印, 苑淑渝, 等. 核素内辐射治疗后肿瘤控制概率计算模型的研宄[J]. 中华放射医学与防护杂志, 2001, 21: 367-370. DOI:10.3760/cma.j.issn.0254-5098.2001.05.019 |
| [4] |
Valley JF, Kvshelevsky AP, Lerch P. A method for the calculations of beta-ray dose[J]. Health Physics Pergamon Press, 1974, 26: 295-300. DOI:10.1097/00004032-197404000-00002 |
| [5] |
Webb S. Optimum parameters in a model for tumor control probability including interpatient heterogeneity[J]. Phy Med Biol, 1994, 39: 1895-1914. DOI:10.1088/0031-9155/39/11/007 |
| [6] |
Kneschaurek P. The influence of repopulation kinetics on isoeffect doses for permanent implants[J]. Strahlenther Onkol, 1994, 170: 02-607. |
| [7] |
Steel GG and Stephens TC. Stem cells in tumours Stem cells: their identification and characterizationed CS Potten (Edinburgh: Churchill Livingstone)[C], 1983.
|
| [8] |
Buffa FM, Fenwick JD, Nahum AE. An analysis of the relationship between radiosensitivity and volume effects in tumor control probability modeling[J]. Med Phys, 2000, 27: 1258-1265. DOI:10.1118/1.599003 |


