核设施在正常运行或事故时可能流出放射性物质污染环境, 使工作人员和附近居民受到来自空气中或地面的辐射照射。为了评估流出物对人的辐射危害, 需要估计受照人员的剂量, 本文研究空气浸没照射的情况。
早期估计空气浸没照射人的剂量是采用各向同性点源并对源区积分的方法[1], 这种方法适用于无限均匀放射性烟羽照射条件, 未考虑地面和人体对辐射场的影响, 并且只能估算体表剂量。
为估计人体深部器官的剂量, 美国核管理委员会(NRC)提出了简化的方法, 即把空气剂量经5cm厚组织的吸收及质能吸收系数校正后, 视为人体深部器官的剂量[2]。这种方法也没有考虑人体和地面对辐射场的干扰。
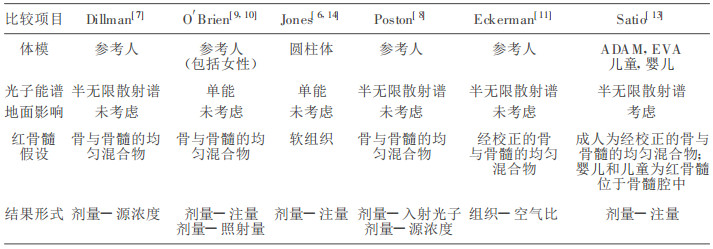
为了计算人体多种器官或组织的剂量, 人们设计了不同的人体模型[3~5], 利用蒙特卡洛方法模拟光子在环境介质和人体内的运输过程, 计算得到体内的剂量分布[6~14], 表 1给出了这方面的部分文献资料。
|
|
表 1 空气浸没照射器官剂量的文献资料 |
从表 1可见, 不同文献采用的人体模型, 光子谱和红骨髓结构假设不同, 给出结果形式也不一致, 难以在实际中应用。本文通过数学处理方法, 对有关文献报道的照射条件, 计算器官剂量的方法和结果进行了分析比较, 并给出了实用的参数。
2 器官剂量与辐射量的关系 2.1 与自由空气辐射场注量的关系在剂量计算中, 注量是一个基本的物理量, 其它量如源浓度和空气吸收剂量都可与之联系起来, 因而器官剂量与注量之间的关系是重要的。Poston给出的是入射体模表面单位光子的器官剂量[8], 即D/ N, 而O′Brien给出的是自由空气辐射场每注量光子的器官剂量[9, 10], 即D/ϕ。入射体模表面的光子注量由于人体存在的影响仅为自由空气辐射场注量的1/4[15], 因此, 在各向同性(ISO)照射条件下, 可应用下式将入射体模表面单位光子的器官剂量, 转换为自由空气辐射场单位注量光子的器官剂量[6]:
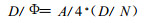
|
(1) |
式中, A为体模表面积。
图 1给出了本文根据Posto n的结果计算得到的自由场单位注量的皮肤剂量和O′Brien结果的比较。从图中可看出, 能量小于40keV时, 二者的结果一致; 能量大于40keV时, O′Brien的结果大于Poston的结果。产生这种结果的原因是由于二者使用的光子谱不同, Posto n使用单能光子在空气中的散射谱, 而O′Brien则是单能光子直接入射体模。能量较低时, 光子与空气的作用以光电吸收为主, 这样散射光子基本上由单能初始光子组成, 二者结果一致; 当能量较高时, 光子与空气的作用以康普顿散射为主, 形成能量从0到初始能量的散射光子谱, 由于散射谱的平均能量小于初始能量, 使得Poston的结果比O′Brien的小。
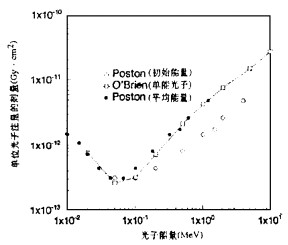
|
图 1 单位注量光子的皮肤剂量随光子能量的变化 |
为了定量地比较二者结果, 本文采用了两种方法。方法一是将散射谱的平均能量对应的器官剂量与单能光子的相比较; 方法二是将单能光子的器官剂量在散射谱上求平均后, 与初始能量光子的器官剂量相比较。根据散射谱计算的平均能量与初始能量的关系见文献[17]。将平均能量对应的皮肤剂量也绘于图 1中, 平均能量和单能光子给出的器官剂量一致。用方法二计算的结果也表明, 二者具有相同的结果。
图 2给出了Poston和O′Brien计算的卵巢和子宫的剂量随光子平均能量的变化, 二者的结果是一致的。卵巢和子宫的剂量与皮肤的相比要小, 并且结果比较分散, 显然是由于卵巢和子宫位于人体较深的部位, 人体浅层组织对辐射的屏蔽作用较大, 统计误差较大所致。卵巢剂量和子宫剂量相比, 能量较高时二者比较接近, 能量较低时子宫剂量要小于卵巢剂量。这说明器官剂量与器官质量关系不大, 而与器官的位置密切相关; 能量较低时, 体积大的器官剂量比体积小器官的剂量小, 这是由于低能时大器官自身屏蔽作用的结果。
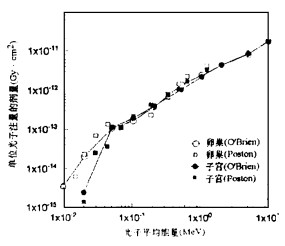
|
图 2 单位注量光子的卵巢和子宫剂量随光子平均能量的变化 |
在估计受放射性流出物照射的人体器官剂量时, 常用的参数是单位浓度放射性物质所致的器官剂量率, 即剂量率转换因子, 因为通常可通过大气扩散理论或实际测量可以得到核素浓度, 用剂量率转换因子乘以核素浓度就可得到人体的器官剂量。Poston[8]和Saito[13]都给出了不同初始能量光子照射条件下以源浓度归一的器官剂量。图 3和图 4分别是根据他们的结果得到的源浓度为1Bq·m-3的皮肤和小肠的剂量。
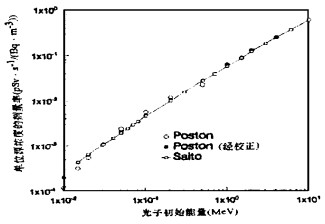
|
图 3 单位源浓度的皮肤剂量随光子初始能量的变化 |
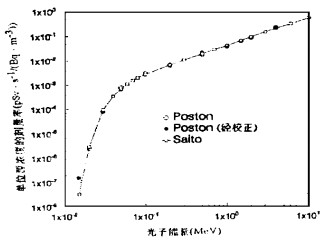
|
图 4 单位源浓度的小肠剂量随光子初始能量的变化 |
从图中可以看出, 当光子能量小于30keV时, Poston的结果比Saito的小, 能量在30keV到0.5MeV之间时, Poston的结果比Saito的大, 能量更高时的结果基本相同。出现这种情况的原因是由于Poston在计算剂量中, 不管能量如何, 都认为半无限空气浸没的光子注量是无限空气浸没光子注量的1/2。
实际上, Poston的分析只对较高能量的光子成立(0.5MeV以上), 因为此时光子的平均自由程远比人体大, 未散射光子注量为无限空气浸没照射时的一半; 散射光子中能量较高的部分占多数, 而康普顿散射与原子序数不是很敏感, 可以认为散射光子也为无限空气浸没散射光子的一半, 这样总的光子注量就为无限空气浸没照射的一半。对于能量很低的光子(小于10keV)其平均自由程已小于人体的高度, 此时半无限空气浸没可当成无限浸没处理, Poston的结果将低估实际值最大可达1倍。对于中等能量的光子, 散射辐射所致的剂量大部分由比初始能量更低的光子引起, 而低能光子与物质相互作用以光电吸收为主, 土壤的原子序数比空气大, 吸收作用比空气强, 这样从土壤散射回空气的光子将少于空气散射到土壤的光子, 使空气的光子注量少于无限空气浸没散射光子的1/2, 这样, Poston的结果将高估了实际值。
为了校正地面的影响, 可用半无限空气浸没照射与无限空气浸没照射空气吸收剂量之比作为剂量校正因子[16]。剂量校正因子是光子初始能量的函数。校正后Poston的剂量亦绘于图 3和图 4中, 与考虑地面影响的Saito计算的结果一致。
2.3 与空气吸收剂量的关系在实践中, 容易得到的辐射监测量是空气吸收剂量或照射量, 因此, 如果知道器官剂量与空气吸收剂量之比(器官-空气剂量比), 那么就可根据空气吸收剂量估计受照人体的器官剂量。
在求器官-空气剂量比时, 不必考虑地面的影响, 因为它对器官剂量和空气剂量产生的影响程度相同, 二者的比值可消除这种系统误差。单位浓度半无限空气浸没照射的空气吸收剂量率为:
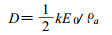
|
(2) |
式中, D为空气吸收剂量率, E0为光子初始能量, ρa为空气密度, k为单位换算常数。
图 5是根据(2)式以及Poston[8], Eckerman[11]和Saito[13]的结果计算得到的皮肤-空气剂量比。
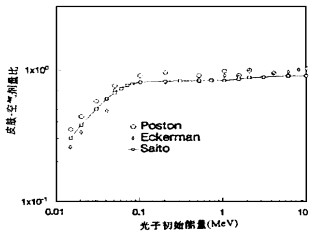
|
图 5 皮肤-空气剂量比随光子初始能量的变化 |
由图 5可见, 不同研究给出的结果有15%左右的差别, Poston的结果最大。原因是计算中对空气密度采用了不同的数值。由(2)式知空气吸收剂量与空气密度成反比, 这样器官-空气剂量比与空气密度成正比。Poston使用的密度值为标准温度和压力下的值1.293g/cm3, Eckerman的是20℃和100kPa压力下的密度值1.189, Saito的为1.204。这样Poston的结果要高出约9%。器官-空气剂量比还有一个重要的特点, 即当光子能量较高时(大于50keV), 器官-空气剂量比随能量的变化不明显, 这样对于流出物照射这样的复杂条件, 只要能量较高的光子占多数, 就可以不考虑能谱的影响, 用测得的空气吸收剂量乘以相应的器官-空气剂量比, 得到该器官的剂量, 这在实际应用中具有重要意义。
3 红骨髓模型的影响红骨髓是人体辐射敏感的组织, 它存在于骨髓腔中, 其分布不仅随骨骼的位置变化, 而且与年龄密切相关, 很难给出接近实际情况的红骨髓分布模型, 因此在计算中多采用简单的软组织近似或骨骼和软组织均匀混合物来近似。图 6给出了本文根据Poston[4], Saito[13]和Jones[14]三位作者的结果计算得到的红骨髓-空气剂量比。
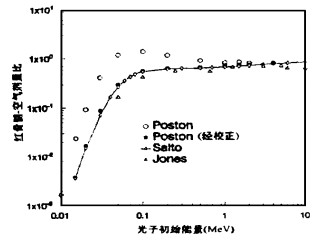
|
图 6 红骨髓-空气剂量比随光子初始能量的变化 |
由图 6可知, Poston的结果最大, Saito的结果居中, Jones的结果最小。原因是由于三者采用的红骨髓模型不同。Poston采用骨骼与红骨髓均匀混合物模型, 这种模型没有考虑到骨骼对红骨髓的屏蔽作用。Saito采用的模型与Poston的相同, 但对计算结果做了骨骼屏蔽校正。Jones则采用简单的软组织模型, 由于混合物的质能吸收系数比软组织大, 在相同辐射场条件下混合物的剂量大于软组织的剂量, 这样Jones的结果最小。
从图 6中还可看出, 在能量大于0.2MeV时, 混合物模型与软组织模型给出的结果基本一致, 但小于此能量时, 混合物剂量比软组织剂量表现出更强的能量相关性。这是因为低能时骨骼内的钙和磷等元素的光电吸收作用影响, 使得未经骨骼屏蔽校正的混合物剂量要高估软组织剂量数倍, 即使经过屏蔽校正也还是要高估一些。
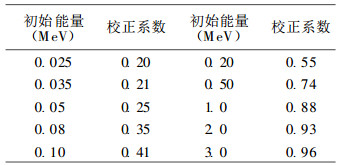
Saito计算了考虑骨骼屏蔽和不考虑骨骼屏蔽两种条件下ADAM的红骨髓剂量。本文根据这些结果导出了红骨髓剂量校正系数。Kerr也给出了光子能量0.2MeV以下男性参考人的剂量校正系数[17], 与本文由Saito的结果计算的校正系数相比, Kerr给出的值在能量大于50keV的偏高。将两者结合起来, 给出对混合物模型的剂量校正系数(表 2), 利用此表可对混合物模型给出的红骨髓剂量进行校正。将Posto n的结果校正后亦绘于图 6中, 可见混合物模型给出的红骨髓剂量经校正后与Saito的结果一致。
|
|
表 2 用于红骨髓混合物模型的剂量校正系数 |
O′Brien计算人体器官剂量使用的体模是ICRP男性参考人和女性参考人[3], Saito在计算中使用了四种体模一成人男性和女性[4], 婴儿和儿童[5]。O′Brien的结果表明, 对于环境辐射照射的器官剂量, 由ICRP男性参考人与女性参考人模型大小和质量不同引起的器官剂量差别在5%左右。Saito计算的男性和女性成人体模的差别也在5%左右, 与Saito的结果相同。这是因为成人男性和女性体模是经ICRP男性参考人和女性参考人改进得到, 模型的总质量与体积基本未变, 只是个别器官的位置和尺寸进行了调整, 以适应外照射剂量估算的需要。成人男性器官剂量与儿童的相比, 能量在100keV以上时差别小于20%, 但对深部小器官可达50%, 有效剂量当量相差20%以内。婴儿由于体积更小, 质量更轻, 其器官剂量与成人的相差更大, 二者相差程度明显依赖于器官位置和射线能量。对于深部小器官, 二者可相差几倍; 对位于浅表和体积较大的器官, 二者相差平均为40%。
总之, 体模越大, 器官剂量越小; 光子能量越低, 器官位置越深, 体模的影响程度就越大。显然, 这是由于人体自身屏蔽作用的结果。
对位于身体表面的器官皮肤则是一个例外, 体模大小对其剂量几乎没有影响, 其原因可由(1)式导出。(1)式中, D/N为入射体表单位光子的器官剂量, 它等于单位光子在皮肤上沉积的能量除以皮肤质量(即皮肤面积、厚度和密度三者的乘积), 与皮肤面积成反比。因此D/ϕ与皮肤面积无关, 亦即与体模大小无关。
5 小结在有关计算空气浸没照射人体器官剂量的现有资料中, 由于不同作者采用的计算方法和考虑的影响因素不同, 给出的结果存在较大的差别。目前ICRP和ICRU尚未提出这方面的权威性报告, 本文对现有的文献资料进行了研究, 提出了在应用这些资料时应注意的几个问题。
5.1散射谱照射的器官剂量与单能光子的器官剂量是不同的, 为应用单能光子的器官剂量, 可将其在散射谱上求平均。
5.2在以源浓度归一化器官剂量时, 必须对地面和空气密度的影响进行校正。
5.3采用骨骼和红骨髓均匀混合物模型计算的红骨髓剂量, 必须对骨骼的屏蔽作用进行校正。
5.4器官剂量的大小与体模的尺寸和重量有关, 若用ICRP男性参考人估计成年女性, 特别是儿童和婴儿的器官剂量时, 其结果偏低, 低估程度从5%到数倍不等, 在应用中也应予以考虑。
| [1] |
Binford F T, Barish J, Kam F B K. Estimation of radiation dose following a reactor accident[J]. ORNL-4086, 1968. |
| [2] |
NRC. NRC Regulatory Guide 1. 109, Rev. 1. Calculation of annual doses to man from routine releases of reactor effluents for the purpose of evaluating compliance with 10 C F R Part 50, Appendix Ⅰ.
|
| [3] |
ICRP. Report of the task group on reference man[M]. ICRP Publication 23.Ox ford: Pergaman Press.
|
| [4] |
Kramer R, Zankl M, Williams M, et al. The calculation of dose from external photon exposures using reference human phantoms and monte carlo methods.part Ⅰ:the male (Adam) and female (Eva) adult mathematical phantoms[J]. GSF-Bericht S-885, 1982. |
| [5] |
Veit R, Zankl M, Petoussi N, et al. Tomographic anthropomorphic models.part Ⅰ:construction technique and description of models of an 8 week old baby and a 7 year old child[J]. GSF-Bericht 3/89, 1989. |
| [6] |
Jones T D, Poston J W. Isotropic and cloud source irradiation by monoenergetic neutrons and photons[J]. Health Phys, 1978, 34: 83. DOI:10.1097/00004032-197801000-00009 |
| [7] |
Dillman L T. Absorbed gamma dose rate for immersion in a semi-infinite radioactive cloud[J]. Health Phys, 1974, 27: 571. DOI:10.1097/00004032-197412000-00005 |
| [8] |
Poston J W, Snyder W S. Amodel for exposure to a semi-infinite cloud of a photon emitter[J]. Health Phys, 1974, 26: 287. DOI:10.1097/00004032-197404000-00001 |
| [9] |
O'Brien K, Sanna R. The distribution of absorbed dose-rates in humans from exposure to environmental gamma rays[J]. Health Phys, 1976, 30: 71. DOI:10.1097/00004032-197601000-00007 |
| [10] |
O'Brien K, Sanna R. The effect of the malefemale body size difference on absorbed dose-rate distributions in humans from natural gamma rays[J]. Health Phys, 1978, 34(1): 107. |
| [11] |
Eckerman K F, Kerr G D. Organ Doses from isotropic and cloud sources of gamma rays[J]. Health Phys, 1980, 39: 1054. |
| [12] |
Kocher D C. Dose-rate conversion factors for external exposure to photons and electron[J]. N U REG/CR-1918, 1981. |
| [13] |
Saito K, Petoussi N, Zankl M, et al. Calculation of organ doses from environmental gamma rays using human phantoms and monte carlo methods:part Ⅰ:monoenergetic sources and radionuclides in the ground[J]. GSF-Bericht 2/90, 1990. |
| [14] |
Jones T D. CHORD Operators for cell-survial models and insult assessment to active bone marrow[J]. Radiat.Res, 1977, 71: 269. DOI:10.2307/3574672 |
| [15] |
Jacob N, Harvel W. Radiation level and fluence conversion factors[J]. Health Phys, 1972, 23: 183. DOI:10.1097/00004032-197208000-00007 |
| [16] |
Jeffey C R, Richard E F, Kenneth S. Air-ground interface effect on γ-ray submersion dose[J]. Health Phy s, 1981, 41: 759. DOI:10.1097/00004032-198111000-00005 |
| [17] |
Kerr G D. A Review of organ doses from isotropic fields of γ-rays[J]. Health Phys, 1980, 39: 3. DOI:10.1097/00004032-198007000-00001 |