放射诊断和治疗中, 人们希望建立一个, 体系, 使得散射介质中任一点的剂量都可依据放射源的输出而计算出来。除蒙特卡罗方法以外, 人们通过实验测量及经脸技术得到许多更有实用价值的方法, 包括百分深部剂量、散射函数、组织一空气比、散射-空气比等。
最早引入这个概念称之为“肿瘤一空气比” [1]。组织一空气比(Tissue-air ratio, 下简称TAR)作为剂量学的一个基本物理最, 在计算旋转治疗中转动轴上的剂量时尤为有用, 与推导出的其它类似的物理最, 在放射诊断和治疗中得到了广泛的应用。
1 组织-空气比的定义和特性 1.1 定义体模内给定点的吸收剂量Dd与移去体模后空间中同一点上小块组织内的吸收剂Da之比。
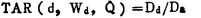
|
在国际辐射单位与测量委员会(ICRU)的定义中, 指出自由空气中该点被一小块组织包围以便建立最大电子平衡。对于同一线质Q而言, TAR是深度和该深度上射野Wd的函数[2, 3]。
1.2 特性 1.2.1对于低能辐射, TAR随深度增大而连续地减少。对于较高能量的线束, TAR在最初几厘米随深度的增加而增加, 达到最大剂量深度后, 连续减小[4]。
1.2.2TAR随射野增大而连续地增大, 但到某一射野时, 有饱和趋势, 如60Coγ射线当射野增至50cm×50cm时, TAR即呈现出饱和的趋势。矩形射野的TAR值比明同面积的圆形射野的小[5]。零射野的TAR函数在半对数座标中是一条直线[6]。
1.2.3TAR与源皮距(SSD)无关。因为总的散射辐射主要取决于一次散射, 预计到达计算点总辐射儿乎与源的距离无关。ICRU建议同一线质辐射的一个TAR数据表可适用于除距离极小外的所有源-轴距。这一点在旋转治疗剂量学估算中非常有用[1-3]。
1.2.4与百分深部剂量的关系。当SSD为无穷大时, 100×TAR=PDD(百分深部剂最); 当深度为最大剂量深度时, TAR=B(rm)(表面反散射因子), 表面反散射因予就是电子平衡上的TAR[4]。
2 TAR数据的测量 2.1 常规照射条件影响TAR测量结果的因素很多, 包括辐射源的特性、探侧器的响应、体模材们和射线的统计涨落等。Gupta和Cunningham用60Coγ照射水体模测量了深度0.5cm~30cm、射野至35cm~35cm的TAR数据[6], 其他研究者也得出了与之符合较好的结果。Hale在为NBC医学物理数据手册推荐X射线的TAR数据时, 比较了4名不同研究者的测量数据, 由于使用不同的实验条件, 包括不同的X射线发生器、靶角度、过滤板和体摸材料, 各组数据仅在10cm和16cm深度上符合的很好。[7, 8]
2.2 大射野TAR定义中包含了这样一个假设, 即TAR应在无限大体摸中侧出, 同时空气中的侧量除源本身和准直器外, 没有来自任何一点的散射辐射。对大射野照射, 上述条件很难实现。实验表明, 射野为160cm×50cm、距地面70cm的空气中吸收剂量测量有1%的误差, 且地面散射受射野和过滤材料影响较大[5]。大射野的侧量要给出一个平衡的射野, 必须加入均整过滤板, 而过滤板的材料和厚度都对测里结呆产生影响。在80cm源-轴距、射野40cm×40cm的60Coγ机, 其平衡区域内的剂盘分布与小射野有很大的差别, 最大剂量点出现在深度为1~2 mm上, 而不是在5mm。选择中等原予序数、厚度为0.4g/cm2左右的过滤板, 可消除电子污染, 改善射线的平衡特性[9]。
2.3 高能X射线测量高能X射线吸收剂量时, 电离室探头必须带有平衡帽。平衡厚度对6MV的X射线是1.5cm, 并随能量的增加而增加, 这时平衡帽材料本身已对测量产生落响, 而且当射野小于平衡帽时, 实验无法进行。对于高能射线, 则用另一个量来代替TAR[10]。
2.4 体积相关TAR全身照射(TBI)的剂量学有其特殊的要求, TAR的概念是基于中心轴线上的剂量计算, 在TBI有限体模厚度的照射条件下使用有局限性。Vrtar等在研究大射野测量点周围散射中心的特殊剂量分布时发现TAR受局部周围材料影响, 即体积相关。60Coγ体摸实验测量结果显示, 体积相关的局部TAR与在无限大体积条件下测出射野大于50cm×50cm的数据有明显差别。由于来目周围散射辐射相对减少, 测出腹部至脚局部深度为10cm时TAR下降15.9%, 腹部至肩深度为8cm下降9.9%。在不同的区域内, 中心平面剂量测出的结果与真实受照情况更加接近。休积相关的TAR提高了体内局部剂量的计算精度, 并用于骨髓移植前的全身照射体内剂量学[11]。
3 TAR教据的计算除蒙特卡罗方法外, 对于常规照射条件的TAR值可从深度剂量和反散射因子计算得出。在实际应用时, 希望借助简单的公式计算TAR数据, 随数字计算机的日益发展, 公式计算占用内存少、省时且计算插值更方便、准确。
3.1 Pfalzner 60CoγTAR经验公式
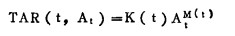
|
上式中, TAR是深度t和射野At的连续函数, K(t)和M(t)是随深度连续减小的列表常数。
Glover改进了上式的计算, 令:
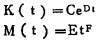
|
其中, C、D、E、F是半值层(HVL)的列表常数。上式在t≥4cm、At≥16cm2计算TAR的修正因子大于0.996[12]。
3.2 Melski 60CoγTAR深度函数公式
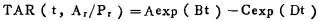
|
其中, A、B、C、D是对应于射线在体模表面面积和周长之比Ar/Pr的列表常数。计算值与测量值比较, 修正因子大于0.9999[13]。
3.3 Thomas适用于60Coγ至15MVX射线的经验公式
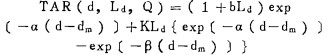
|
其中, β=1/〔X十(L(d-M)Y〕, Ld= ZWdHd/(Wd+Hd), b、α、β、K、X和Y都是对应于辐射线质Q的系数[14]。
4 由TAR导出的其它物理量 4.1 组织一体模比(TPR)TAR作为剂量学的一个基本物理量有两个方面的不足, 第一是为使用TAR, 需要在空气中进行剂量刻度, 这不符合ICRU关于位于深部肿瘤进行放疗用的射线应在体摸内刻度的建议; 其次, TAR最初的定义是组织内一点的剂量与空气中同一点的剂量之比, 这与ICRU的定义不完全相同, 特别是高能X射线, 两个定义因测量用的平衡材料对射线的衰减和散射而得出不同的结果。为此, Karzmark建议用组织一体摸比TPR替代TAR对高能光子的剂量学估算。其定义为:体模中某给定点的吸收剂量与照射条件相同的体模中某一固定参考深度的吸收剂量之比。它可通过某一射野在参考深度上的TAR推算出来。体模刻度方法不受电子污染或来自准直器软辐射的影响, 可以改善放疗部位的剂量学计算精度。同TAR相比, TPR更适于高能光子的剂量学计算。通常采用5om的参考深度, 对能量至20MV的X射线都能满足建立电子平衡的条件[15]。
Saundeas等指出, TPR的定义不应只限定一个参考深度, 还应限定一个参考射野。经限定参考射野而修改后的组织一体模比MTPR在计算中心轴上剂量时可基本消除因不同射野而带来的误差[16]。
4.2 组织一最大剂量比(TMR)Holt等提出组织一最大荆最比(TMR)的撰念, 定义为体模内任一点处的吸收剂盆与最大剂t点处的最大吸收剂t的比值, 它与刻度方法和机器的特殊参数无关。同TAR和TPP相比, TMR更适于计算高能线束[10]。
TMR是从TPP推导出来的, 引入一个固定的最大剂是深度而解决了参考深度的间题, 但如果射野或5sD变化导致最大剂盆深度改变, 那么就不能认为TMR与SSD无关, 为此, 又引入了衰减因子q, 对某一射线质而言,
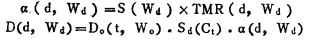
|
式中, S(Wd)和S(Ct)分别是体模散射和准直器散射修正因子。α适用于高能X射线束的计算, 且与源一靶距离无关[10]。TMR相比, α的特性与TAR更为相似。
4.3 散射-空气比(SAR)SAR是从TAR导出的一个量, 用于计算体模中某点的散射剂量。
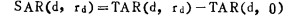
|
TAR(d, 0)表示深度d处、射野半径为0的组织一空气比, 即射线的散射体积近似为零时, 只剩下射线的初级成份。TAR描述了射线的综合效应, 而SAR只考虑其散射效应。SAR不能直接侧量, 可通过散射函数、散射因子和TAR计算得出。与TAR类似, 5AR也仅依赖于辐射线质、深度和射野, 与SSD无关。使用SAR计算均匀射线或非均匀射线对均匀体摸或非均匀体模的散射剂量取得了较好的结果[17]。与TMR类似, 散射一最大比(SMR)的概念也用于高能X射线的散射剂量的计算[18]。
5 剂量学上的应用临床剂量学的精度应在以5%内, 各部分误差应小于2%。以TAR为基础的计算方法完全能达到该精度要求。
5.1 计井中心抽线上任意深度的剂量值
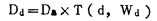
|
在与源和计算点的连线垂直的不规则射野平面内, 经过计算点引N条半径与射野周线相交, 则到达Q点的剂量DQ为[1]:
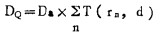
|
对于肺、骨骼等非均匀体剂量修正首先是假定受照介质是均匀的, 然后计算非均匀效应修正因子CF[2, 3]。
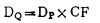
|
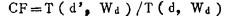
|
d’是等效水的厚度, d是材料实际厚度。
5.3.2 Batho法[19, 20]
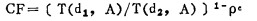
|
ρe是非均匀体相对于水的电子密度。
5.3.3 等效TAR法
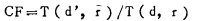
|
d’、r分别是深度和射野半径的比例刻度值。
最初的线性衰减、等剂量位移和有效TAR法, 只考虑了射线的初级成份, 而忽视了散射成份的平衡变化。Bath。法利用TAR和相对电子密度, 间接地考虑了散射成份的变化, 用于高能射线计算得出了最好的数据(在任何临床条件下的60Coγ射线计算修正因子误差在3%以内)。等效TAR法利用CT扫描所提供的非均匀体图象象元信息, 考虑到了非均匀体的形状、大小和位置, 而且, 它可以表示成卷积的形式, 用快速富立叶变换(FFT)技术在三维辐射体内计算非均匀体效应, 对低能光子计算得出较好的结果。以上方法用TMR代替TAR进行计算, 可进一步提高精度。
6 结束语组织一空气比的提出为剂量学计算提供了一些有效的方法, 并且用于高能X射线、全身照射和非均匀性的剂量修正其计算结果愈来愈精确。完善利用组织一空气比方法的剂量学估算, 笔者认为还需做以下一些工作:
1.建立常规照射条件下统一的TAR、TPR、TMR和SAR等标准数据;
2.得出计算TAR等物理量更简单、更精确的经验公式;
3.对于高能线束、大射野全身照射和大深度等特殊照射条件下的TAR等物理量的特性做进一步研究;
4.建立完整的标准计算方法和临床放射剂量学计算之间的修正关系。
| [1] |
Johns HE, et al. Dosage calculations for rotation therapy with special reference to cobalt-60[J]. The Ameriean J Roentgenology Radium Therapy Nuelear Med, 1956, 75(6). |
| [2] |
ICRU Report No.23, 1973
|
| [3] |
ICRU Report No.24, 1976
|
| [4] |
Johns HE.The Physics of Radiology.3rd ed, 1969
|
| [5] |
Van Jake, et al. Dosimetric considerations of very large cobalt-60 fields[J]. Int J Radia Oneology Biol Phy, 1980, 6: 753-759. DOI:10.1016/0360-3016(80)90236-9 |
| [6] |
Gupta SK, et al. Measurement of tissueair ratios and seatter funetions for large field sizs for cobalt 60 gamma radiation[J]. Brit J Radiol, 1966, 39: 7-11. DOI:10.1259/0007-1285-39-457-7 |
| [7] |
Hale John. Survey of tissue-air ratio data: A review of the literature of diagnostie radiology[J]. Med Phys, 1991, 18(6): 1154-1155. DOI:10.1118/1.596625 |
| [8] |
Harrison RM. Comment, on "Survey of tissue-air ratio data:A review of the literature for diagnostic radiology" by John Hale[J]. Med Phys, 1992, 19(3): 589. DOI:10.1118/1.596913 |
| [9] |
Philip MK et al.Use of eleetron filters to improve the buildup charaeteristics of large fields from cobalt-60 beam.Med.Phys., Vol 4, No 5, Sep/Oct, 1977;441-444
|
| [10] |
Garrett Hlot J. The extension of the concept of tissue-air ratios(TAR)to high-energy X-ray beams[J]. Radiology, 1970, 96: 437-446. DOI:10.1148/96.2.437 |
| [11] |
M Vrtar et al.Improvement in TBI in vivo dosimetry using the volume dependent TAR concept.IAEA-SM-298/70: 241-248
|
| [12] |
Glover JR. A more general form of the Power law for tissue/air ratios[J]. Phy Med Bio1, 1966, 11(4): 607-608. DOI:10.1088/0031-9155/11/4/412 |
| [13] |
Melski John. Tissue-air ratio formulae in Co-60 teletherapyd dosimetry[J]. Brit J Radio, 1970, 43: 825-826. DOI:10.1259/0007-1285-43-515-825 |
| [14] |
Thmas RL. A general expression for megavoltage central axis depth doses[J]. Brit J Radiol, 1970, 43: 554. DOI:10.1259/0007-1285-43-512-554 |
| [15] |
Karzmark CJ. Correspondenee[J]. Brit J Radiol, 1965, 38: 158-159. DOI:10.1259/0007-1285-38-446-158 |
| [16] |
Saundeas JE, et al. Central axis depth doses for a constant source-tumour distance[J]. Brit J Radiol, 1968, 41: 464-467. DOI:10.1259/0007-1285-41-486-464 |
| [17] |
Cunningham JR. Seatter-air ratios[J]. Phy Med Biol, 1972, 17(1): 42-51. DOI:10.1088/0031-9155/17/1/005 |
| [18] |
Khan Faiz M, et al. Revision of tissuemaximum ratio and seatter-maximum ratio concepts for cobalt 60 and higher energy X-ray beams[J]. Med Phys, 1980, 7(3): 230-237. DOI:10.1118/1.594648 |
| [19] |
Batho HF. Lung corrections in cobalt 60 beam therapy[J]. J Canadian Assoeiationd Radiol, 1964, 15(6): 79-83. |
| [20] |
Sontag Mare R, et al. The equivalent tissue-air ratio method for making absorbe dose calculations in a hetcrogeneous[J]. Radiology, 197, 8129: 787-794. |


