辐射损伤研究中细胞存活率曲线与剂量的关系, 需要有相应的数学模型作定量描述。为提高工作效率和研究水平, 本文介绍描述辐射剂量对细胞损伤存活率曲线的几种数学模型, 供从事辐射细胞生物学研究的科技人员选用。
一 数学模型描述辐射剂量对细胞存活率曲线的数学模型, 有两个学派:生物物理学派和损伤修复学派[1]。生物物理学派是建立在经典的靶细胞学说基础上的, 它着重分析各种射线损伤所致细胞的死亡规律, 提出细胞敏感靶的概念; 损伤修复学说则把细胞的修复机制引入数学模型, 因而受到学术界的普遍重视。
(一) 由靶学说提出的数学模型1.单靶单击模型[2]
在电离辐射对细胞作用的研究中, 在许多情况下, 常用所谓单靶模型来描述一次击中所需的照射剂量, 其模型表达式为:
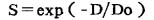
|
(1) |
式中, Do称为“平均致死剂量”, 它的倒数为曲线的斜率。这种关系也存在于辐射对病毒或酶照射后的钝化效应中, 此时Do称为钝化剂量。从(1)式知, 当剂量D=Do时, 上式的值为:
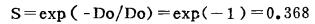
|
因此, Do这个平均致死剂量也可理解为使细胞存活率达到36.8%所需的照射剂量, 这个剂量可简明地作为细胞(细菌或病毒等)对射线敏感性的一个指标。一般来说, 此模型适用于描述由高LET电离辐射(如α粒子)所致细胞存活率曲线[3]。
2.多靶单击模型[1]
该模型用于描述带有肩宽的人和哺乳动物细胞剂量一存活率曲线较好。数学式为:
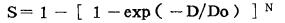
|
(2) |
式中, Do亦称为平均致死剂量, N称为靶数或击中数。当N=1, D=Do时
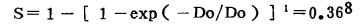
|
这与单靶单击模型相同。但若N>1, D=OD时, 细胞存活率将大于0.368;例如, N=2, S=0.600;N=3, S~0.747。因此, 该模型在D=Do时, 细胞存活率不是一个常数, 在此模型中, 另有一个描述细胞亚致死性损伤修复能力的参数, 称之为肩宽剂量(shoulder dose)Dq, 即
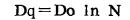
|
(3) |
3.带初始斜率的多靶模型
该模型最初是由Bender[4]和Kelleer[5]提出的, 其表达式为:
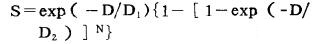
|
(4) |
式中, D1描述单靶单击生物效应, 它的倒数即为初始斜率, D2描述多靶生物效应, 它的倒数即为存活曲线的第二个斜率。显然该模型是单靶模型与多靶模型的乘积。
Do, Dq分别由(5)和(6)式求出:
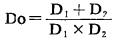
|
(5) |
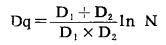
|
(6) |
本实验室的经验说明, 用该模型来拟合细胞剂量一存活率曲线, 在多数情况下可得到比较好的结果。
4.线性一平方模型(LQ)
该模型是建立在二元理论或NDA双链断学说基础上的又称α、β模型, 其表达式为:
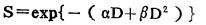
|
(7) |
它是由Sinclair(1965)提出的[6]。据文献报导, β值与肩区宽度, 即与细胞修复能力有关; α值主要影响存活率曲线指数下降部分[1]。该模型表达简明, 计算简单。
(二) 由修复学说提出的数学模型无论是多靶(或它的改良型一带初始斜率多靶)模型, 还是线性一平方模型, 都不能反映辐射(或其它作用因子)对生物体作用的一个重要特征一剂量率效应, 即随剂量率的降低, 相同剂量照射的细胞存活率将会提高。引起剂量率效应的本质是细胞本身具有修复辐射损伤的能力。Thames(1985)提出的不完全修复模型(IR)[7]和Cuitis (1986)提出的致死一潜在性致死模型(LPL)[8], 反映了上述重要的生物学特征。
1.不完整修复(IR)
LQ模型s=exp[-(αD+βD2)中的α项反映单个粒子径迹引起的损伤, 而β项(即平方项)反映了两个独立的径迹引起的两个亚损伤相互作用产生的损伤, 两个亚损伤之间的时间间隔(取决于剂量率)和第二个亚损伤出现之前对第一个亚损伤的修复(取决于修复能力)均会影响细胞的最终的存活率。因此, β项实际上将受到细胞修复能力和剂量率的影响。但是这个模型中的参数α、β只与细胞本身的特性有关, 反映不出照射条件(照射次数、剂量率)、细胞修复能力的影响, 而Thames提出的不完全修复模型可解决上述间题, 此模型的表达式为:
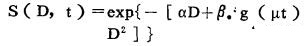
|
(3) |
其中函数
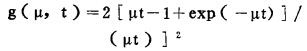
|
(9) |
式中D为照射总剂量, t为照射时间, t=D/P, P为剂量率, μ称之为修复速率常数。这样, 将细胞存活率与照射总剂量和剂量率两个变量联系起来, 不仅可获得修复速率常数, 而且还可得到半值修复时间, 即
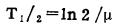
|
(10) |
对(8)式, 联系到第(9)式取极限, 当t→∞时, 有
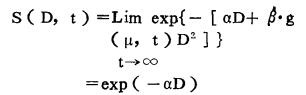
|
(11) |
此式代表了完全修复情况下的细胞剂量一存活率曲线。由于t→∞, 因此, 只有在剂量率十分低时, 这种情况才会发生。当t→O时, 则有
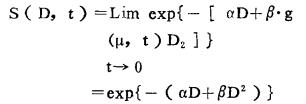
|
此时存活率曲线演变成前面所述的线性-平方模型, 这种情况只有在高剂量率照射条件下才会出现。
2.致死一潜在致死性模型(LPL)
辐射对细胞造成导致细胞生殖性死亡的损伤可分成两类:一类称之为“致死性”损伤, 它们是不能被细胞自身的修复系统所修复的; 另一类称为“潜在致死性”损伤, 它们是可以修复的, 但有几种可能的命运:①正确修复导致细胞的存活; ②错误修复而演变成致死性损伤; ③在得到修复前它们可以相互作用或与氧或与其它化学修饰剂(例如增敏剂)反应而变成致死性损伤。反映细胞损伤与修复的这一过程称之为“致死一潜在致死性模型, (Lethal, Potentially Lethal Model, LPL)。该模型可以给出单位吸收剂量在细胞至产生一个致死性(LD)或潜在致死性(LPD)损伤的概率, 以及单位时间内潜在致死性损伤被正确修复的平均速率常数和潜在致死性损伤相互作用而演变成致死性损伤的平均速率常数。
根据本实验室的经验, 用不完整修复模型来描述细胞存活率往往比用致死潜在致死模型的效果为好, 并且后者的数学表达式较复杂, 计算比较麻烦。据此, 后面所设计的计算机处理程序不包括致死一潜在致死性模型。
二 计算方法及程序设计 (一) 计算方法上述细胞剂量一存活率曲线各种模型中参数值的计算方法, 均先由计算机自动给出初值, 再用阻尼最大二乘法进行迭代运算[9], 给出各待定参数值, 模型初值的确定方法列在表 1中。
|
|
表 1 辐射剂量-细胞存活率曲线数学模型及初值的确定方法 |
根据上述模型和计算方法的要求, 具体设计并编制了计算机程序。该程序配有汉字显示和输出, 可在IBM-PC/XT、AT及共兼容机上在25行中文系统下直接运行。程序运行的流程见图 1。
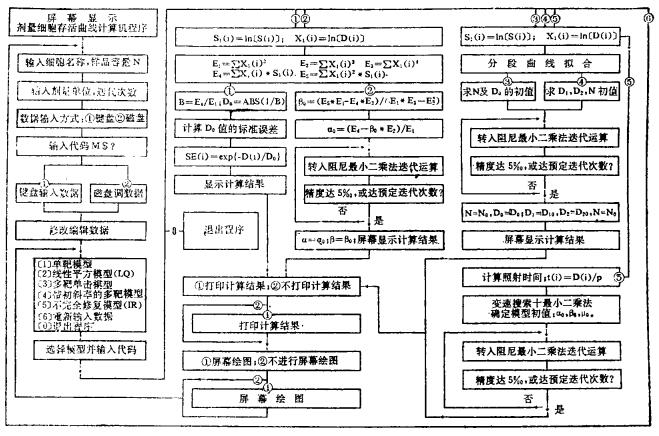
|
图 1 辐射剂量-细胞存活曲线拟合程序流程图 |
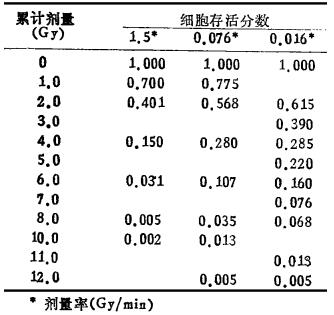
作为举例, 为了说明采用不同数学模型对与剂量率有关的实验数据进行处理的后果, 此处引用了文献[10]中提供的人体黑色素瘤细胞株HX118, 分别经高、中、低剂量率照射后细胞的存活率数据(见表 2), 以本文列出的不同数学模型进行曲线拟合, 比较各个模型描述细胞存活率曲线的优缺点。
|
|
表 2 XH118细胞受不同剂量率照射后细胞存活分数 |
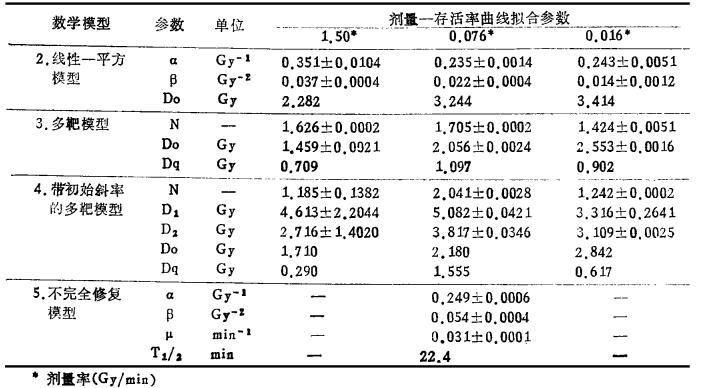
将表 2所列数据输入计算机, 分别用模型2-5进行曲线拟合, 各个模型拟合的参数值列在表 3。从表中可见, 三个不同剂量率照射细胞的存活率, 用线性平方模型, 多靶单击模型和带初始斜率的多靶模型, 均得到较好的拟合结果, 其相关系数(r)都在0.99以上, 残差平方和(Q)均小于1.37×10-2以下(见表 4)。但是, 用同一个数学模型对不同剂量率照射下细显存活率曲线进行拟合时, 获得的参数是不同的。虽然也有其规律性, 例如, 上述3个模型的Do值均随剂量率的降低而增大, 线性平方模型的β值随着剂量率的降低而明显变小等。这些都说明, 随着剂量率的降低细胞对辐射敏感性亦降低。但是上述模型中的参数, 不能反映在剂量率不同条件下引起的细胞对辐射敏感性的变化。而考虑了修复机制的不完全修复模型(IR), 则可将3组不同剂最率下的细胞存活率数据拟合成单一的剂量-效应方程, 获得一组参数(见表 3), 用这组参数能综合反映3组剂量率下的细胞存活率曲线, 见图 2。从表 3和图 2可见, 该模型参数不仅反映了细胞固有的辐射敏感性, 而且还考虑了细胞对辐射损伤的修复能力, 可给出修复速率常数μ和半值修复时间T1/2。因此, 对不同剂量率照射到细胞存活率实验数据的处理, 用IR模型比用其它3个模型更能反应辐射损伤的本质。在实际研究工作中, 凡需要了解某种细胞对辐射的敏感性和修复能力的, 宜用IR模型来描述。
|
|
表 3 4个数学模型时XH118细胞剂量-存活率曲线拟合参数的比较 |
|
|
表 4 4个模型拟合优度的比较 |
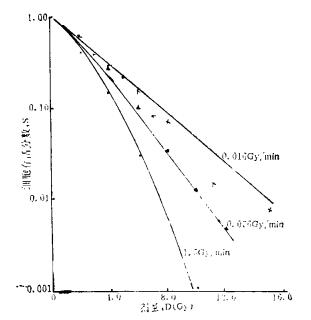
|
图 2 不完全修复模型对不同剂量率下HX118细胞存活曲线拟合值与照射剂量的关系 |
值得指出的是, 本文用IR模型拟合得到的参数与文献[10]的结果有一定的差异, 这可能与计算精度不同有关。本文设计的程序, 在计算机自动给出参数初值后, 再转入阻尼最小二乘法进行反复迭代运算, 当迭代精度达到5‰以下时, 当前的值即为模型参数的解。因此, 上述3个剂量率下细胞存活率数据用本文程序拟合的精度较文献[10]给出的精度高。例如, 以残差平方合Q的大小为例, 文献[10]的Q值为0.226, 本文的Q值只有0.0259, 差不多小一个数量级。
还要指出的是, 用靶学说提出的几个数学模型来处理同一批数据, 所获得的Do值差别是很大的。因此, 不同条件下的实验数据, 只有用同个数学模型获得的Do值才有比较的义意。
| [1] |
李冬华, 等. Hela细胞系辐射剂量-细胞存活曲线和数学模型[J]. 中华放射医学与防护杂志, 1982, 2(6): 5. |
| [2] |
杨纪柯编著.数理统计方法在医学科学中的应用, 上海科学技术出版社, 1964, 101-103
|
| [3] |
刘国廉, 等. Pu-238α粒子辐射体体外诱发大鼠肺成纤维细胞恶性转化[J]. 中华放射医学与防护杂志, 1990, 10(6): 383. |
| [4] |
Bendes MA, et al, Int J Radiat Biol 1962 5: 133.
|
| [5] |
Kellerer AM, et al, Radiat Res 1971;47: 15.
|
| [6] |
Sinelar WK, Teehieal Report Series No 58 Biophysical Aspects of Radiation Quality, IAEA Vienna 1966: 21.
|
| [7] |
Thames HD. An "incomplete-repair" model for survival after fractionated and continuous irradiation[J]. Int J Radiat Biol, 1985, 47(3): 319-339. |
| [8] |
Curtis SB. Lethal and potentially lethal lesions induced by radiation-A unified repair model[J]. Radiat Res, 1986, 106: 252. DOI:10.2307/3576798 |
| [9] |
中国科学院计算中心概率统计组: 概率统计计算, 第一版, 北京: 科学出版社, 1979;160.
|
| [10] |
沈恂, 等. 反应修复特性的细胞存活曲线的数学模型及其计算机程序[J]. 中华放射医学与防护杂, 1991, 11(6): 374. |