在剂量测量中，如何使测量数据可靠、准确、高精度，并给出测量误差，是众所关心的。由于测量仪器、人员、环境的不同，测量误差可能有大有小，但我们需要尽可能减少误差，提高测量的准确性。

测量误差可分为偶然误差和系统误差。偶然误差包括人员过失误差和仪表的瞬时非正常误差，这种误差不易消除，只能通过仔细地工作和统计学处理尽量缩小；系统误差包括刻度误差、量程误差、读数误差、气温气压误差、方向误差、能量响应误差、时间响应误差和探测器有效中心位置确定误差，这种误差可以通过修正而减少。

一 刻度误差

包括表头的刻度误差和校准传递误差。表头的刻度误差随着仪表的级别不同而不同，校准传递误差随校准实验室级别不同而不同。校准时由校准单位给出校正K值，。一般表头误差：Ⅰ级≤1 %，Ⅱ级≤3%；K值误差，国家级≤1 %，次级标准级≤3 %。

由于机械表头的动力靠游丝的弹性，游丝的力矩在表头的两端与受力的线性较差，而在满刻度的30~70 %内线性较好，因此表针要在满刻度30~70%的范围内读数，测量读数才较准确。

二 量程误差

使用不同的量程测量同一个量，会出现不同的读数。在较好的仪器，这种差别较小，但较差或陈旧的仪器则相反。因此要注意修正，或利用不同的K值进行修正。

三 读数误差

由于表针与刻度盘都有一定的距离，测量者站在不同的位置读数是不一样的。读数时两眼应平视，使视线与指针平行，如刻度盘由镜象反映，应在指针与镜象重合时读数。读数读到最小刻度的1/2即可，仔细时也只能估计到最小刻度的1/4，并不是读数位数越多越好。为了减少偶然读数等误差，应以3次以上读数均值为测量值，并舍去3倍标准差以外的读数。

四 气温、气压误差

校准仪器给出的K值是按标准气温（0℃）、气压（1.013×10^-5Pa）计算的，实际测量场所不可能与此相符，其修正值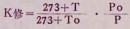，其中TO、Po为标准气温、气压，T、P为测量时的气温、气压。

五 方向误差

由于探测器几何条件的不完全对称性，探测器在辐射场中放置的方向不同，读数将不一样。校准时，一般以探测器的轴线与入射线方向呈180°时（以²²⁶Ra或⁶⁰Coγ射线照射）响应系数为1，其他方向的响应系数与此归一。

六 能量误差

由于射线的能量不同，不同的仪器或同种仪器测量读数亦不会相同，这叫能量响应。一般以²²⁶Ra（或⁶⁰Co）γ射线能量响应系数归一。

X、γ射线剂量仪表在100~200keV的电磁辐射范围内灵敏度较高，会出现能量响应的“峰值”。就其能量响应来说，电离室、闪烁晶体探测器比计数管的要好^[1]，尤其是电离室式的仪器。有的仪器针对不同的电磁辐射加有能量补偿或配备不同的能量平衡吸收片。对于单一能量（谱）辐射源来说，只要知道此能量点的K能值就够了；但对于复合能量辐射源来说，知道各能量点K能值，而不知道其组成比例，其有效K值还是求不出来；对于辐射谱随时、随地变化的辐射场，其有效K值更无法求出。这样的辐射场，只能借助能量响应比较好的仪器解决，象电离室式仪器。

七 时间误差

各种剂量仪表，都有一个电路时间常数。由于时间常数不同，辐射场存在的时间不同，剂量率读数可能不同。- -般说来，剂量测量都为电流测量，测量电流：

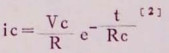
Rc为仪器电路时间常数，一般为2~5秒；Vc为被测量的电压，当t→∞时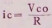，=记作i_○，即为被测量的真实电流量。当t=Rc时，ic =0.632i_○○，t= 2 Rc、3Rc、4 Rc、5Rc时，i_○=0.865i_○○0.950i_○○、0.982i_○○、0.993i_○○。按统计学原理，数据达到实际值的95%就有其代表性，更精确些可要求达到实际值的99%以上，因此当辐射场存在的时间t≥（3~5）RC时，对场时间的要求就可以了。这样长的时间对于X线深部治疗机的要求是可以的，对于医用诊断透视机的要求也勉强可以，而对于医用诊断摄片机的要求根本达不到，所以医用诊断摄片机的场所剂量测量用剂量率测量是不行的。

对于瞬间存在的辐射场所的测量应如何解决呢？可应用具有累积测量功能的仪器来解决。累积剂量的测量是电荷测量，测量的是电容上积累的电荷，

i_○为充电电流，t_○为辐射场存在时间，测量仪表没有对t_○，提出要求，因此使用累积功能测量瞬间存在的辐射场的剂量是对的。

八 探测器有效中心位置确定误差

仪器的读数代表何处的测量数据，该处的位置我们就叫测量的有效中心位置。由于有效中心位置确定的不同，带来的误差叫探测器的有效中心位置确定误差。目前所见的各类进口或国产剂量仪表中，多以圆柱型电离室为常见，其电离室的工作方式多以“顶照”方式为主。如果探测器本身具有有效探测器中心位置的标志，我们可以此标志平面与探测器中心轴线交点，定为探测器的有效中心位置。例如日本的DR-3型类仪器，在电离室前端约1/3处有白线标志。对于无标志线的仪器，我们可以下式计算探测器的有效中心位置。

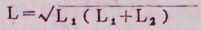
L₁为辐射场源点（或焦点）至探测器前端的距离，L₂为探测器的有效长度，L为探测器有效中心位置至源点的距离。

此种误差在探测器距源点距离较近时，将带来较大的测量误差。

在剂量测量中，对误差不进行修正或测量时不注意误差，测量的误差将可能达到上百、上千倍，这种数据使用价值很低或根本无法使用。进行了误差修正或注意了误差消除，如若测量数据不给出误差范围，这样的数据也无法作出正确评价。因此，剂量测量不仅要给出测量数据，也必须给出误差值。若已知各项测量误差为ai，则根据误差传递公式，总体误差为

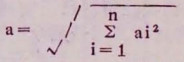
据资料报道，基准误差大约可控制在1%，修正误差可控制在2%，如使误差尽量缩小，并假设误差可以相加，则可产生2~10%的误差，取其平均值7%，因此次级标准实验室测量的误差可控制在9%，而现场测量也只能控制在10%的误差范围。