Medicinal Plant Using Ground State Stabilization of Natural Antioxidant Curcumin by Keto-Enol Tautomerisation

1 Introduction

Curcuma longa Linn (turmeric) is a medicinal plant botanically related to Zingaberaceae family. Turmeric powder derived from the rhizome of Curcuma longa is commonly used as a spice, food preservative and food colouring agent. It also has a long history of therapeutic uses. The compound shows yellow colour in Turmeric are three curcuminoids namely curcumin, demethoxycurcumin and bisdemethoxy curcumin. Curcumin [1, 7-bis(4-hydroxy-3-methoxyphenyl)-1, 6-heptadiene-3, 5-dione], a yellow bioactive pigment is the major component of Turmeric. Curcumin shows some biological activities exhibiting anti-inflammatory [1-5], antifungal, anticarcinogenic, antibacterial [6], antiprotozoal wound healing, antispasmodic, anticoagulant, antitumor and hepatoprotective activities [7-10]. Antioxidant and wound-healing gives by curcumin, its anticancer and anti-viral attributes, its effect on lymphocytes, platlet aggregation, detoxification mechanism. Curcumin is a potential anticancer drug it show its effect through molecular targets and it also cure colon cancer. The water-soluble extract turmerin, inhibits HIV infected T cell proliferation. It has also been studied extensively as a chemo preventive agent in several cancer cells [11-16]. From the figure the acceptor site is the active region to cure cancer cells and also some tumors. Structurally curcuminoids are linear 1, 7-diaryl-1, 6-heptadiene-3, 5-diones which exist in tautomeric forms as α, β unsaturated 1, 3-diketo form and enol form. The proton-transfer of dissociation is associated with radical-scavenging mechanisms of curcumin. The curcumin structure containing enol form supposes to be more stable than diketo form. Curcumin has a potential singlet oxygen quencher at low conditions. The compound has an effect in protecting skin against UV light. The results indicate that unsaturation in the side chain a methoxy group on benzene ring and keto-enol in the curcumin molecule structural. The theoretical also reported wherein DFT and TD-DFT calculations help to find out keto-enol equilibrium of curcumin in solution state and low pKa value for the dissocation of enol proton. Quanta methods are useful in determining the effect of inter molecular interactions on the vibrational spectra. The pervious study explain the understanding of hydrogen bonding that conform spectroscopic approach (FT-IR, FT-Raman) with quantum chemical methods (DFT). Density Functional theory is useful in vibrational assignment, hydrogen bonding, High chemical reactivity (Homo-Lumo) and NMR. The delocalisation of π-electron is further supported by red-shifted UV-visible absorption maximum of keto-enol tautomer of curcumin.

2 Analytical Instruments

The chemicals required were obtained from Sigma Aldrich chemical suppliers and are of analar grade. UV spectra were recorded on a Schimadzu UV-VIS-1601 spectrophotometer. FTIR spectra (KBr pellets) were recorded on 8101 Schimadzu FTIR spectrophotometer recorded in the region 4000-400 cm^-1. FT-Raman spectra have been recorded in the region 3500-50 cm^-1on a Perkin-Elmer spectrometer. The 1H NMR spectra were recorded on a Varian 300 NMR spectrophotometer. The photoluminescence spectra of curcumin deposited on SiO2/Si were recorded at room temperature on a Fluorolog-3 Model FL3-221 spectro fluorometer system (HORIBA Jobin-Yvon). The emission spectra were measured utilizing a 450 W xenon lamp as the excitation source.

3 Computational Details

Advanced geometries of the title compound in the ground state were obtained by the density functional theory (DFT) [17] and B3LYP functional with 6-311++G(d, p) basis set utilizing Gaussian 09 program package. The basis set 6-311++G(d, p) fragmentation by d polarization functions on heavy atoms and p polarization functions on hydrogen atoms have been used [18-20]. Quantum theory of atoms in molecules calculations has been done to predict intermolecular interactions using this software. The conformers analysis, first hyperpolarizability, ¹H, ¹³C and ¹⁷O NMR, HOMO-LUMO and ESP analyses under various electric fields are carried out by B3LYP/6-311G++(d, p) method. The thermodynamic functions such as entropy, enthalpy and the heat capacity where carried out for the different temperatures. Curcumin has two hydrophobic phenyl groups. But the molecule assumes different conformations that can maximize π-π and van der Waals interactions with aromatic and some hydrophobic amino acid residues of proteins [21-25]. Phenolic hydroxyl and methoxy groups, as well as the keto and enol groups present on the ends and in the middle of the molecule has strong interaction as well as directed hydrogen-bonding.

The keto-enol tautomerism introduces additional functionality, with the possibility to locate donor and acceptor groups for hydrogen bonding in many ways. But the α, β-unsaturated keto can serve as a acceptor for nucleophilic attack. The difference between two tautomers is the hybridization of the carbon at the (α) position. While sp² hybridiation is present in the keto-enol tautomer, the diketo tautomer has sp³ hybridisation. Finally, there is intramolecular hydrogen bonding in the keto-enol tautomer, which is absent in diketo tautomer of curcumin. It has been shown that the strength of the hydrogen bond at the keto-enol is strongly correlated to delocalization of π-electron in β-diketones.

4 Results and Discussion

4.1 Molecular Geometry

Fourteen conformers are mainly expected to exist for Curcumin, respectively. The optimized parameters of monomer and dimer structures of Curcumin are represented. Generally geometrical parameters such as bond lengths, bond angles are the important factors in determining the electronic properties of the molecule that are listed in Table 1. The numbering scheme of monomer structures is denoted in Fig. 1 respectively. The optimization of dimer for the title compound is carried out in order to simulate H bonding through phenol group. The optimized structures with inter molecular hydrogen bonds description are given in Fig. 2. The intermolecular interaction is observed between C-H···O and O-H···H. This intermolecular interaction is stabilizing in Curcumin. The bond lengths of C=O are lengthened in dimer optimization [26]. To find the most optimized geometry, the energy calculations are carried out for various possible conformers are listed in Table 2. The conformers of Curcumin are shown in Fig. 3.

Open image in new window

Open image in new window

Open image in new window

4.2 Two Rotor PES Scan Studies

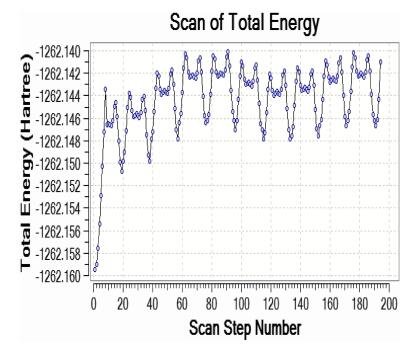
The two rotor potential energy surface (PES) scan with the B3LYP/6-311++G(d, p) level of theoretical approximations was performed for Curcumin is shown in Fig. 4, respectively. The calculated potential energy curves of the molecule in this approach a recent study were consistent with distinct minima that correspond to gauche (-)-gauche-gauche (G1gg), trans-trans-gauche (Ttg), trans-gauche-gauche (Tgg), trans-gauche-gauche (-) (Tgg1) and gauche(-)-gauche-trans (G1gt) conformers in the order of decreasing relative stability. The dihedral angle C35-C34-O6-C5 and C42-C41-O27-C24 for curcumin is also relevant coordinate for conformational flexibility within the molecule. For this rotation minimum energy curves have been obtained at 20°, 40°, 60°, 80°—as shown in Fig. 4 clearly demonstrate that flexibility inside the bonds for curcumin atoms.

Open image in new window

5 Transition State Calculations

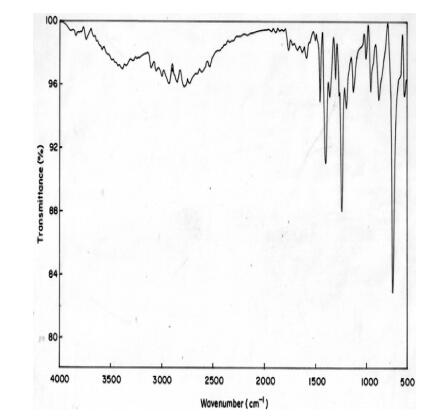
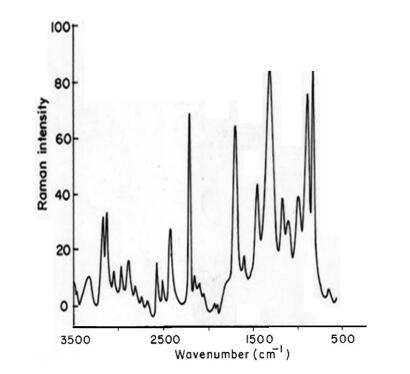
The vibrational spectrum of a transition state is characterized by one imaginary frequency (implying a negative and positive field), which means that in one direction in nuclear configuration space the energy has a maximum, while in all other orthogonal directions the energy is a minimum. The fundamental modes of curcumin along with the calculated IR, Raman frequencies and normal mode descriptions (characterized by TED) are reported in Table 3. The observed and calculated FTIR and FT-Raman spectra of curcumin are performed in B3LYP levels using 6-311++G(d, p) basis set are shown in Figs. 5 and 6. Also, it should be noted that the experimental results belong to solid phase and theoretical calculations belong to gaseous phase.

Open image in new window

Open image in new window

5.1 C-H Vibrations

The aromatic organic compounds structure shows the presence of asymmetric C-H stretching vibrations in the region 3100-3000 cm^-1 [27], which is the characteristics region for recognition on C-H stretching vibrations. In the title molecule, bands have been observed at 2924, 2900 and 3076, 3045, 3023, 2989, 2971, 2965, 2987, 2978, 2945, 2901, 2467 cm^-1 assigned to C-H stretching vibrations in FT-IR and FT-Raman spectra, respectively. The C-H in-plane and out of- plane bending vibrations normally take place as a number of intensity sharp bends in the region of 1300-1000 and 1000-750 cm^-1, respectively. Theoretical Positive field and negative field for C-H in-plane and C-H out-of-plane bending vibrations by B3LYP/6-311++G (d, p) method showed excellent agreement with the spectrum.

5.2 O-H Vibrations

The hydroxyl stretching vibrations are [27] observed in the region around 3500 cm^-1. The peak is broader and its intensity is higher than that of a free O-H vibration, which indicates involvement in an inter molecular hydrogen bond. So the O-H stretching vibrations of curcumin are observed at 3308, 3280 cm^-1 and 3289 in FT-IR and FT-Raman. The in-plane O-H deformation vibration usually appears in the region 1440-1260 cm^-1 in the spectrum, which gets shifted to higher wave number in the presence of hydrogen bonding. The O-H out-of-plane bending vibrations give rise to broadband identified in the region 700-600 cm^-1. Theoretical Positive field and negative field for hydroxyl vibration under goes a large shift due to hydrogen bonding.

5.3 C-C Vibrations

The ring C-C stretching vibrations, usually occurs in the region 1400-1625 cm^-1 [27]. In accordance with above literature data in our present study, the bands for C-C stretching vibrations are observed at 1645, 1569, 1543, 1522 cm^-1and 1712, 1596, 1581, 1555, 1544, 1521 cm^-1 in FT-IR and FT-Raman spectra, respectively. These observed frequencies show that, the substitutions in the ring to some extend affect the ring mode of vibrations. The comparison of the theoretically (Positive field and negative field) values are good agreement with B3LYP/6-311++G(d, p) method. The in-plane and out-of-plane bending vibrations of C-C group are also listed out in the Table 3.

5.4 C=O Vibrations

The interaction of carbonyl group with other groups present in the system did not produce such a drastic and characteristic change in the frequency of C-O stretch as did by interaction of C-C stretch. The carbon-oxygen double bond is formed by pπ-pπ between carbon and oxygen. Because of the different electron negativities of carbon and oxygen atoms, the bonding electrons are not equally distributed between the two atoms. The lone pair of electrons on oxygen also determines the nature of the carbonyl group. The position of the C-O stretching vibration is very sensitive to various factors such as the physical state, electronic effects by substituent, ring strains. Normally carbonyl group vibrations occur in the region 1850-1600 cm^-1 [27]. In this study, the C=O stretching vibrations of curcumin are observed at 1423 cm^-1 in FTIR spectrum. The in-plane and out-of-plane bending vibrations of C=O group have also been identified and presented in Table 3. Positive field and negative field values are correlated with B3LYP/6-311++G(d, p) method.

5.5 CH₃ Group Vibrations

The curcumin molecule under consideration possesses CH₃ groups. For the assignments of CH₃ group frequencies one can expected that nine fundamentals can be associated to each CH₃ group, three stretching, three bending, two rocking modes and a single torsional mode describe the methyl group. The CH₃ symmetric stretching frequency is identified at 2500 cm^-1 in the FTIR spectrum and 2609 cm^-1 in the FT-Raman spectrum for curcumin. The CH₃ in-plane stretching vibrations are identified at 2359 cm^-1 in the FTIR spectrum and 2384 cm^-1 in the FT-Raman spectrum. The CH₃ symmetric bending and CH₃ in-plane bending frequencies are attributed at 1256 and 1345 cm^-1 in the FTIR spectrum and 1212, 1289 cm^-1 in the FT Raman spectrum. The in-plane rocking and out-of-plane rocking modes of CH₃ group are found at 1178, 1156 and 614 cm^-1 in the FTIR spectrum and 632 cm^-1 in the FT-Raman spectrum. The bands obtained at 2250, 2223 cm^-1 and 856, 670 cm^-1 in the FTIR spectrum for curcumin assigned to CH₃ out-of-plane stretching and CH₃ out-of-plane bending modes, respectively. The assignment of the bands at 540 and 579, 373 cm^-1 in the FTIR and FT Raman spectrum for curcumin attributed to methyl twisting mode.

5.6 NMR Data Analysis

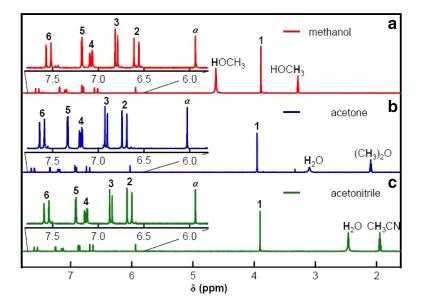
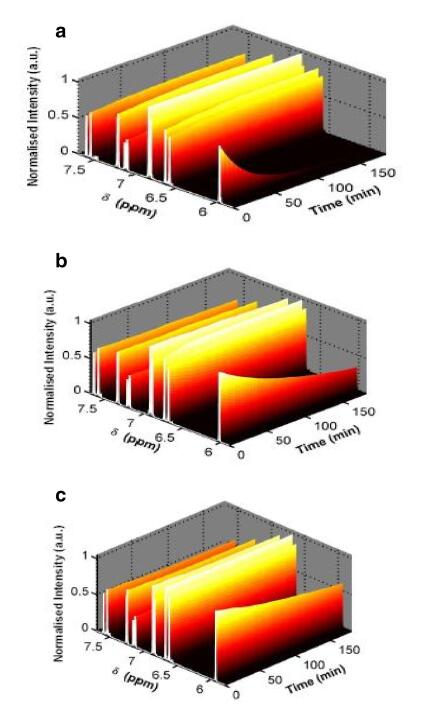
The isotropic chemical shifts are frequently used as an aid in identification of reactive ionic species. It is acknowledged that accurate predictions of molecular geometries are essential for reliable calculations of magnetic properties. The calculated chemical shifts for ¹³C, ¹H, and ¹⁷O NMR are shown in Table 4. The calculations reported here are performed in methanol solution, rather than in the gas phase, using IEF-PCM model. ¹H atom is mostly localized on periphery of the molecules and their chemical shifts would be more susceptible to intermolecular interactions in the aqueous solutions as compared to other heavier atoms. Aromatic carbons give signals in overlapped areas of the spectrum with chemical shift values from 100 to 150 ppm [28-30]. In this study, the theoretical chemical shift values of aromatic carbons except C11 of Cur cumin are in the range of 98.3004-143.6594 ppm in the solvent. The chemical shift of C4 (143.1092 ppm in Methanol and 143.6594 ppm in Acetonitrile) is greater than the other aromatic carbons because of the substitution of OH group in Curcumin. The C25 and H32 atoms are deshielded due to the presence of electronegative oxygen in the OH group. Due to shielding effect which is the non-electronegative property of hydrogen atom, the chemical shift values of ring carbon atoms are lower than C4 and C14. The chemical shift values of aromatic protons are in the range of 6.5193-8.9553 ppm in Cur cumin for the solvents. The chemical shift value of H16 is very smaller than the aromatic protons since it is attached with electronegative atom, oxygen O31 of Cur cumin. The hydrogen atoms present in phenol group of Cur cumin experience little more shielding than other aromatic hydrogen atoms. ¹⁷O has a very wide chemical shift range which for small molecules partially compensates for its broad signals. The chemical shift of ¹⁷O is ranging from -40 to 1120 ppm [31]. In the title compound, the peaks at 370.0681 and 367.4292 ppm are assigned to O33 which is phenol group oxygen of the methanol and acetonitrile compounds. The chemical shift magnitude of methanol and acetonitrile 209.3890 and 210.3421 ppm is indicating the presence of hydroxyl oxygen (O43) of Cur cumin. Noticeably, the oxygen chemical shift of phenol group is larger than other oxygen due to the environment. Chemical shift (δ) of the collected NMR spectra were referenced to the residue proton resonance of the corresponding solvents, which are δ=3.31, 2.05, 1.94 and 3.33, 2.08, 1.99 ppm for the pentet proton signal of the two methyl group in methanol, acetone and acetonitrile, respectively. Assignments of the ¹H NMR spectra of curcumin in methanol, acetone and acetonitrile are shown in Fig. 7. The time-dependent ¹H NMR spectra of curcumin in methanol, acetone and acetonitrile from δ=8.5 to 5.0 ppm recorded at 45 ℃. It is clear that the intensity of the Hα peak, which has a δ of approximately 6 ppm, decrease as function of time in all three solvent. But methanol takes 3 h at 45 ℃ as shown in Fig. 8a and acetone, acetonitrile at 45 ℃ as shown in Fig. 8b, c. The Fig. 9 shows the decrease in Hα area in methanol, acetone and acetonitrile at several temperatures. The decrease in intensity of the Hα signal is proportional to the decrease of concentration of curcumin. The rate constant of tautomerisation of curcumin in methanol, acetone and acetonitrile at various temperatures are shown in Table 5. The rate constant of tautomerisation of curcumin in acetone are larger than that in acetonitrile at same temperature, indicates faster conversion of keto-enol to diketo tautomer of curcumin of acetone.

Open image in new window

Open image in new window

Open image in new window

5.7 UV-Vis Spectral Analysis

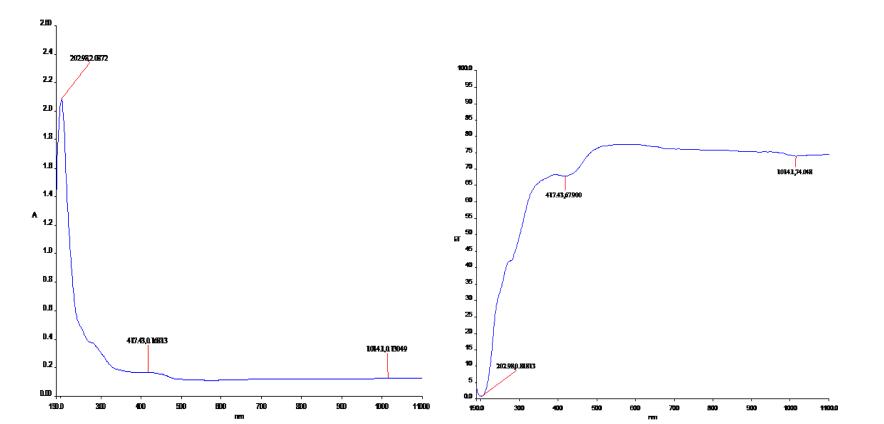
The visible and UV spectra of curcumin represent transitions between electronic energy levels. The transitions between a bonding or lone-pair orbital are non-bonding or anti-bonding orbital. But the absorption bandwidth could indicate the degree of agglomeration [32]. So the electronic absorption corresponds to the transition from the ground to the first excited state and is mainly described by one electron excitation from the highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital (LUMO).Electronic transitions are usually classified according to the orbitals engaged or to specific parts of the molecule involved. Common types of electronic transitions in organic molecules are π-π^*, n-π^* and π^*(acceptor)-π (donor). For Curcumin the UV-Vis absorption and transmisson spectra have been studied and show three intense peaks of 202, 417, 1014 nm for Ethanol and THF in Table 6. Observed band at 417 nm is due to the π-π^* transition. The less intense band centered at 202 nm is due to the partly forbidden n-π^* transition. The more intense band observed at 1014 nm is described to an allowed π^*- π transition. Based on the above photo absorption theory, the frontier molecular orbitals (FMO_S) of the molecule have been investigated according to the results obtained from the B3LYP/6-311++G(d, p) calculations. The experimental absorbance and transmittance UV-Vis spectra are shown in Fig. 10. It also gives us the hint that the charge recombination should also be taken into account besides the widely considered criteria to design and screen of new efficient molecule for experimentalist.

Open image in new window

5.8 Transport Properties

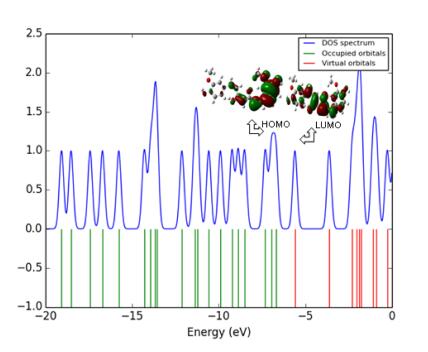
The spatial distribution of the frontier orbital is a three dimensional representation of local electron density of the molecule. The highest occupied molecular orbital (HOMO), the lowest unoccupied molecular orbital (LUMO) are the frontier orbital's, the difference between them are known as HOMO-LUMO gap (HLG). HLG determines the transport properties of the molecule. Large decrease in the HLG predicts the possibility of having reasonable conduction through the molecule, since, the conductivity increases with decreases in HLG. So the field increases (0.00-0.15 VÅ^-1) the HLG extensively decreases by using Gaussian 09 programme package. Figure 11 illustrates the spatial distribution of the molecular orbital of the molecule. Table 7, shows the small HLG exists in this molecular system, the possibility of conduction through the molecules is found to be very less, therefore, it almost act as an insulator.

Open image in new window

5.8.1 Electric Fields on HOMO-LUMO Analysis

The analysis of the wave function is mainly described by one-electron excitation from the highest occupied molecular orbital (HOMO) to the lowest unoccupied molecular orbital. HOMO-LUMO analysis of these compound is done at B3LYP/6- 311++G(d, p) level of theory for the zero field and fields of 0.05.01 and 0.15 VA^-1. Figure 11 illustrates the orbital distributions of HOMO and LUMO levels of the title compound for the zero field and biasing steps of 0.05.01 and 0.15 VA^-1. HOMO is delocalized mainly on ring carbons; the oxygen of hydroxy also takes part in the formation of HOMO of curcumin for zero fields. The strong electron withdrawing group O of polyphenol group attracts the charge density while on other hand electron donating group hydroxy is attached on left hand of curcumin which would strengthen the donor ability. Hence LUMOs are distributed on the polyphenol group. In Curcumin, HOMO is delocalized mainly on ring carbons and there is no distribution of HOMO on polyphenol group. Figure 11 shows that there is no electronic projection in HOMO and LUMO over the ring hydrogen atoms of the compound in zero fields. The values of HOMO energy, LUMO energy and HLG are used as an indicator of kinetic stability of the molecule. Which shows that substituted hydroxyl have no effect on the title compound. When the field increases (0.0-0.15 VA^-1), the HOMO-LUMO gap (HLG) extensively decreases from 0.06853 to 0.0345 eV for curcumin, respectively (Table 7). This large decrease in the HLG implies that the possibility of having reasonable conduction through the molecule, hence the conductivity increases with decreases in HLG. The variation of HLG with applied the electric field is also verified with density of states (DOS) spectrum. Figure 12 shows the density of states (DOS) for zero field, 0.05, 0.1 and 0.15 VA^-1.The green and red lines in the DOS spectrum are indicating that the HOMO and LUMO levels. The value of HLG measured in DOS spectrum is almost the same with the calculated value by Gaussian 09 W program package [33-35]. The DOS spectrum also shows that HOMO-LUMO gap decreases as increase in electric field. Further insight into the chemical reactivity analysis in relation to their electronegativity, chemical hardness and their aromaticity difference would assess the suitability of application process in curcumin.

Open image in new window

5.9 Mullliken Charges

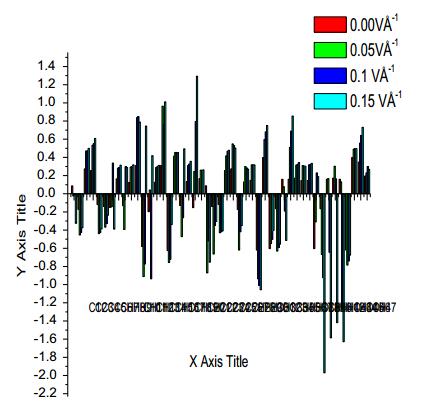
The Mulliken psychoanalysis is the finest population analysis method. The electron population of each atom of the molecules is identifying, because of calculating the mulliken charges are explained by the density functional methods. The charge distribution of the Curcumin gives the Carbon and Hydrogen charges had both signs. Oxygen atoms have negative charges in all basic sets, which are donor atoms. Mulliken atomic charge computation play a vital role in the relevance of quantum chemical calculation to molecular system because of atomic charge effect, dipole moment, molecular polarizability, electronic structure of the molecular systems. By using the Gaussian output shown in the Table 8. The molecule has different charge distribution with respect to the dynamic basic sets for quantum calculations. The predicted atomic charges are in graphical representation (Fig. 13). To change the basic set, the charge distribution should be changed. The charge change with origin set due to polarization For illustration, the charge of H(16) and H(19) atoms are -0.3390e, 0.3577e at B3LYP/6-311+G(d, p) in the title compound curcumin. Thus the charges of the atoms are not varied according to electric field. Charge migration to heavy atoms can be related to molecular interactions in curcumin molecules.

Open image in new window

5.10 Nonlinear Optical Properties

The hyperpolarizability (β), dipole moment (μ) and polarizability (α) were calculated using B3LYPmethod with 6-311++G(d, p) basis set on the basis of the finite-field approach. The complete equations for calculating the magnitude of total static dipole moment (μ), Vector-first hyperpolarizability (β_vec), the anisotropy of the polarizability (Δα) and the First hyperpolarizability (β), using the x, y, z components from Gaussian 09 W output is as follows:

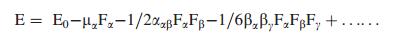
where E₀ is the energy of the unperturbed molecule, F_α is the field at the origin, and μ_α, ααβ and βαβγ are the components of dipole moment, polarizability and the first order hyperpolarizabilities, respαectively [36]. The total static dipole moment μ, and the mean first hyperpolarizability (β) using the x, y, z components, they are defined as:

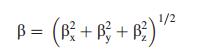
where

The first hyperpolarizability is calculated using B3LYP/6-311G++(d, p) method. Since the value of hyperpolarizability (β) of the Gaussian 09 W output is reported in atomic units (a.u.), the calculated values have been converted into electrostatic units (esu) (β: 1 a.u.=8.639×10^-33 esu). The first hyperpolarizabilities of curcumin are 3.0450 × 10^-30 esu, respectively and are presented in Table 9. The first hyperpolarizability values of title compound are greater than that of urea (μ and β of urea are 1.3732 Debye and 0.3728×10^-30 esu obtained by B3LYP/6-311++G(d, p) method). Comparatively, first hyperpolarizability shows that curcumin is suitable for nonlinear optical studies.

5.11 Molecular Electrostatic Potential (MEP)

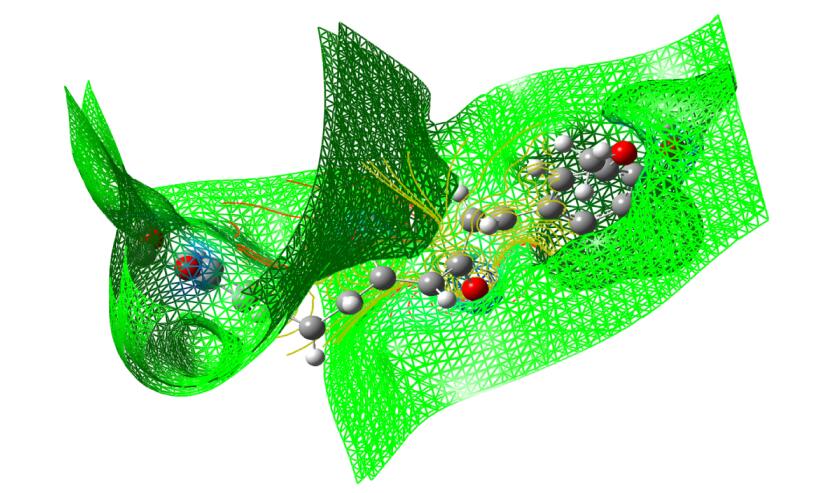
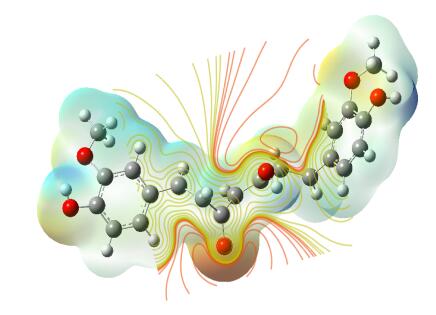
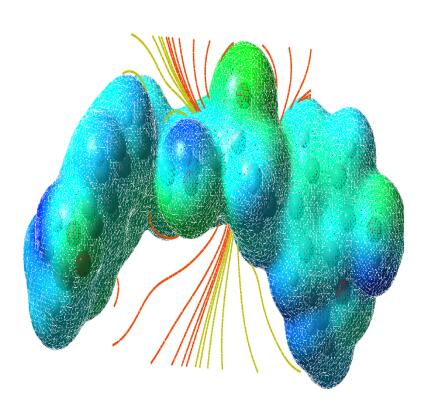
The molecular electrostatic potential is related to the electronic density and is a very useful descriptor for determining the sites for electrophilic and nucleophilic reactions as well as hydrogen bonding interactions [36]. To predict reactive sites of electrophilic or nucleophilic attack for the investigated molecule, the MEP at the B3LYP/6-311++G(d, p) optimized geometry was calculated. The various values of the electrostatic potential at the surface are represented by various colors. The color scheme for the MEP surface is red-electron rich, partially negative charge (electrophilic reactive center); blue-electron deficient, partially positive charge; light blue-slightly electron deficient region (nucleophilic reactive center); yellow-slightly electron rich region; green- neutral, respectively. The potential increases in the order red < orange < yellow < green < cyan < blue. It can be seen that the negative regions are mainly over the N atoms. The negative (red and yellow) regions of the MEP are related to electrophilic reactivity and the positive (blue) regions to nucleophilic reactivity, as shown in Figs. 14, 15 and 16. As can be seen from the figure, this molecule has several possible sites, C and O atoms for electrophilic attack. The importance of MESP lies in the fact that it simultaneously displays molecular size, shape as well as positive, negative and neutral electrostatic potential regions in terms of color grading and is very useful in research of molecular structure with its physiochemical property relationship.

Open image in new window

Open image in new window

Open image in new window

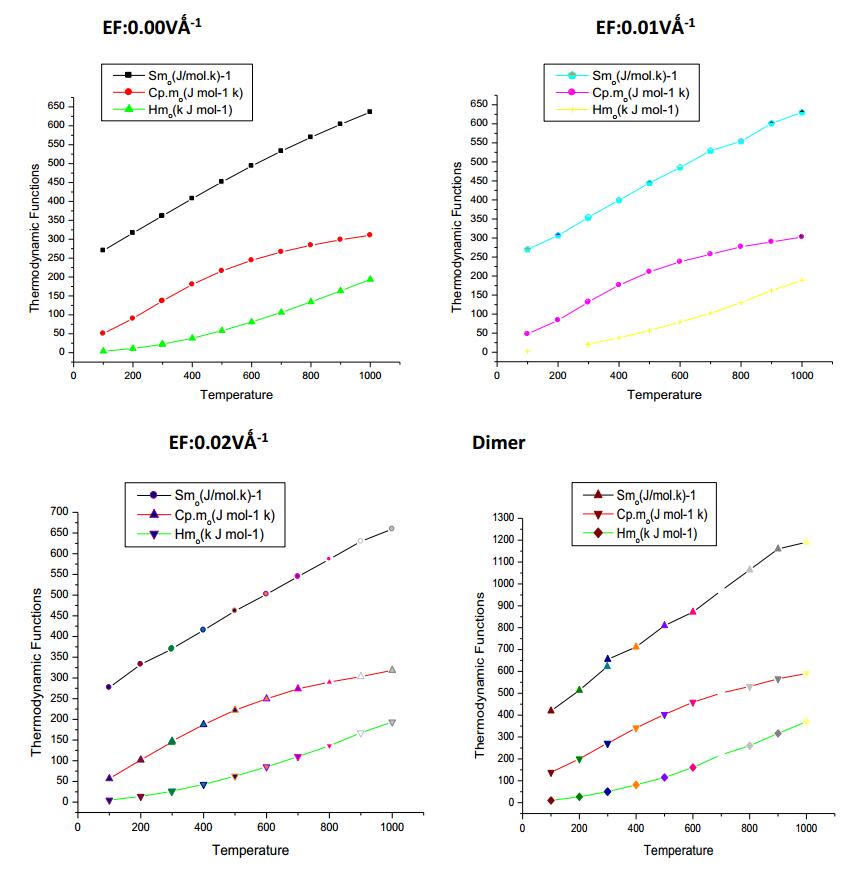
5.12 Thermodynamic Properties

Standard statistical thermodynamics function, heat capacity (C_{p, m}⁰), entropy (S_m⁰) and enthalpy changes (H_m⁰) (monomer and dimer) were computed at B3LYP/6-311++G(d, p) basis set by using perl script THERMO.PL [37] and are listed in Table 10. Thermodynamic functions are all values increasing with temperature ranging from 100 to 1000 K due to the fact that the molecular vibrations intensities increase with temperature. The correlation equation among heat capacities, entropies, enthalpy changes with temperatures were fitted by quadratic formulas and the corresponding fitting factors (R²) these thermodynamic properties are respectively. The correlations plot of those shown in Fig. 17. The thermodynamic correlation fitting equation is follows: Moreover, the thermodynamic properties indicate that the curcumin molecule is more reactive and more polar. The correlation graph for zero (monomer and dimer) applied EFs are shown in Fig. 17 and the corresponding fitting equations are as follows:

Open image in new window

6 Conclusion

The stabilities of the curcumin are analysed by PES scan. The vibrational frequencies of the fundamental modes of the compound are precisely assigned and analysed and the theoretical results are compared with the experimental frequencies. The energies of important MO's, absorption wavelength, oscillator strength and excitation energies of the compound are also determined from TDDFT method and compared with the experimental values. The electric field influence is noticed in HOMO-LUMO gaps of curcumin. The HOMO-LUMO gap extensively decreases from 0.06853 eV to 0.0345 eV for curcumin, respectively as the electric field increases. The first hyperpolarizabilities of curcumin are 3.17 and 3.0450×10^-30 esu, respectively. Hα of curcumin was used in NMR in methonal, acetone and actenitrile. The dependence between the rate constant of tautomerisation of curcumin are studied. Photoluminescence has longer wavelength due to the stabilization of the excited states. MEP study shows that the electrophilic attack takes place at the O position of curcumin.

Notes

Acknowledgements

The authors gratefully acknowledge to HOD, PG & Research Department of Physics, AA Govt Arts College, Villupuram, provided the necessary facility to complete this work.

Declaration

Own fund used in this article. We are not arising any fund from any other agency.