2. 成都理工大学 地球物理学院, 成都 610059
2. College of Geophysics, Chengdu University of Technology, Chengdu 610059, China
地下空间的高分辨率成像是地震采集、处理的最终目标[1-2]。由于地表条件和地下介质的复杂性及速度分析、静校正、动校正等处理方法的限制,处理后的叠前地震道集仍然存在剩余时差,表现为同相轴校正不平,这种资料难以满足叠前偏移、叠前反演等处理、解释的需求,会影响地震资料的成像精度。曲寿利[3]指出动校正方法本身的局限性、速度分析误差和薄层调谐均是引起剩余时差的主要原因,并提出了一种基于统计方法的剩余时差校正方法。周鹏等[4]对国内外相关方法技术进行总结,将剩余时差校正方法归纳为精细速度分析、地震道集互相关技术、相位匹配技术和统计法等4类。石战战等[5]提出一种基于动态时间规整(Dynamic Time Warping,DTW)和形状上下文(Shape Context,SC)的剩余时差校正方法,通过SC取代DTW算法中的距离算子,但该算法采用逐点搬家法进行剩余时差校正,直接使用容易造成波形畸变,同时DTW算法对噪声比较敏感,影响规整路径计算的精确性。
由地震子波构造过完备字典,对地震道集进行稀疏表示,其结果(系数矩阵)相当于地下介质的单位冲激响应,类似于地层反射系数,脉冲对应于地层界面,消除了子波影响,而地层信息没有损失,再对系数矩阵作时差校正,就能避免波形畸变。稀疏表示的核心思想是高维空间中的信号可以由低维信号模型来描述[6]。近年来受压缩感知及相关数学理论发展的推动,产生了一系列稀疏表示方法,如匹配追踪[7-8]、基追踪(Basis Pursuit,BP)[9]和稀疏贝叶斯学习(Sparse Bayesian Learning,SBL)等,其中SBL是常用的稀疏表示方法,尤其适用于高相干字典条件下信号的稀疏表示[10],该方法最早是由Tipping[6]提出并证明是最有效的回归和分类方法。Wipf等[10-11]将SBL用于一维信号稀疏恢复,随后将其拓展为基于多测量向量模型(Multiple Measurement Vectors,MMV)的多变量稀疏贝叶斯学习(Sparse Bayesian Learning for MMV,MSBL)算法。与BP算法相比,SBL和MSBL的优势在于其全局最优解同时也是最稀疏解,并且具有较少的局部最小值,在实际信号处理中,稀疏解常具有一定的结构,SBL框架则能够充分利用这些结构,提高稀疏表示的性能。Zhang等[12-13]针对块稀疏信号的块内相关性,提出了块稀疏贝叶斯学习(Block Sparse Bayesian Learning,BSBL),随后通过将MMV模型转化为单测量向量模型(Single Measurement Vectors,SMV)问题,提出了基于TSBL(Time Varying Sparse Bayesian Learning)算法和TMSBL(Sparse Bayesian Learning for Multiple Measurement Vector Model Exploiting Temporal Correlation)算法的联合稀疏表示(Joint Sparse Representation,JSR)方法。TSBL算法和TMSBL算法能够有效地处理时变稀疏(Time-Varying Sparsity)模型[14-15]。
DTW是一种基于动态规划的模板匹配算法,具有简单高效的特点,用于对系数矩阵进行剩余时差校正。由于原始的DTW算法计算效率较低,出现了多种改进算法,众多学者[16-20]通过约束或抽象等方法降低计算量,但DTW算法存在固有缺陷,认为模板匹配的2个信号之间的差异仅由时间畸变引起,估计出的规整路径不够精确,Compton等[21]提出平滑动态时间规整(Smooth Dynamic Time Warping,SDTW),能够估计出更加平滑和精确的规整路径,并将其应用于多波匹配。Cui[22]将SDTW用于自动井震标定。
单纯使用DTW算法难以取得良好的校正效果,将SBL和DTW方法结合,提出一种联合TMSBL和SDTW的叠前道集剩余时差校正方法,该方法从2个方面进行改进:①利用TMSBL对叠前道集进行稀疏表示,对计算出的系数矩阵进行SDTW时差校正,再利用校正后的系数矩阵重构地震数据;②将原算法中的SC-DTW改为SDTW,以期避免波形畸变,同时实现高保真剩余时差校正和随机噪声压制。
1 方法原理 1.1 稀疏贝叶斯学习基于MMV模型的信号JSR的基本数学模型为
| $ \mathit{\boldsymbol{S}}{\rm{ = }}\mathit{\boldsymbol{W X}}{\rm{ + }}\mathit{\boldsymbol{N}} $ | (1) |
式中:S为测量矩阵;W为字典矩阵;X为源矩阵;N为噪声矩阵。
设X具有稀疏性,JSR的目的是通过优化算法恢复出系数矩阵X。受压缩感知和相关数学理论研究推动,产生了多种JSR算法,其中TMSBL是常用的JSR方法之一,该方法适合于地震信号稀疏表示,原因是:①动、静校正后,叠前地震道集中各道反映了同一地质构造的信息,如CMP道集反映了地下同一点的地质信息,因此,系数矩阵具有联合稀疏性,并且有一定的时间、空间结构,TMSBL算法可以较好地利用这些信息,提高稀疏表示的精度;②处理后地震数据常存在剩余时差,系数矩阵的支撑是变化,TMSBL可以较好对这种时变稀疏性进行建模;③由地震子波构造的字典矩阵,相干度较高,对于这类高相干性字典,与其他稀疏表示算法相比,SBL算法具有较好的适应性。
SBL理论框架下,系数矩阵X的每一行都可以用参数化Gaussian分布建模
| $ p\left( {{\mathit{\boldsymbol{X}}_i};{\gamma _i}, {\mathit{\boldsymbol{B}}_i}} \right) = N\left( {0, {\gamma _i}, {\mathit{\boldsymbol{B}}_i}} \right), i = 1, 2, 3, \cdots , M $ | (2) |
式中:p(·)概率密度函数;N(·)表示Gaussian分布;γi为非负超参数,控制系数矩阵X的行稀疏性。
当γi = 0时,对应的Xi (X的第i行)为零,算法迭代过程中,大部分的γi都会变成0,实现了稀疏约束作用,Bi为协方差矩阵,描述Xi时序结构。因此,参数γi和Bi的估计是SBL算法的核心,可以通过二型最大似然法(Type-Ⅱ Maximum Likelihood)进行估计。
直接优化求解式(2)较为困难,实际采用的优化思路是,令
| $ \mathit{\boldsymbol{s}}{\rm{ = }}\mathit{\boldsymbol{D x}}{\rm{ + }}\mathit{\boldsymbol{n}} $ | (3) |
可以看出,式中的X非零行正好对应着中x的非零块,可以采用BSBL算法进行优化。
TMSBL算法和详细推导过程见文献[12],这里仅介绍基本思路。
考虑到式(2)中X每行对应不同的Bi会引起算法过拟合,后续公式推导均采用统一的协方差矩阵B,将公式(1)转化为SMV模型(3)后,向量x的先验概率可以写为
| $ p\left( {\mathit{\boldsymbol{x}};{\gamma _i}, \mathit{\boldsymbol{B}}, \forall i} \right) = {N_x}{\rm{(}}0, {\sum _0}) $ | (4) |
式中:
假设地震噪声为随机噪声,满足Gaussian分布,条件概率密度为Gaussian分布
| $ p(\mathit{\boldsymbol{y}}|\mathit{\boldsymbol{x}};\lambda ) = {N_{y|x}}(\mathit{\boldsymbol{Dx}}, \lambda \mathit{\boldsymbol{I}}) $ | (5) |
式中:参数λ表示噪声方差;I为单位矩阵。
通过Bayesian方法求取后验概率密度也为Gaussian分布
| $ p\left( {\mathit{\boldsymbol{x}}|\mathit{\boldsymbol{y}};{\gamma _i}, \mathit{\boldsymbol{B}}, \forall i} \right) = {N_x}({\mu _x}, {\sum _x}{\rm{)}} $ | (6) |
式中:
当参数γ和B确定后,系数矩阵的最优解可以通过最大后验概率法(Maximum A Posterior,MAP)进行估计。
地震道集中存在剩余时差,系数矩阵的支撑是变化的,须要采用时变稀疏模型进行建模。时变稀疏模型可看作是多个MMV模型串联结果[20-21],因此,TMSBL可以便利地处理时变稀疏信号JSR[14]。
1.2 平滑动态时间规整算法原理DTW算法目的是计算出最优规整路径u = {u1,u2,u3,…,uL}使2个时间序列f = { f1,f2,f3,…,fM}和g = {g1,g2,g3,…,gN}能够最佳匹配,即满足
| $ \mathit{\boldsymbol{f}}[i] \approx \mathit{\boldsymbol{g}}\{ i + \mathit{\boldsymbol{u}}[i]\} $ | (7) |
DTW计算流程分为以下4步:
第1步,构造误差矩阵E ∈ RM×N
| $ e_{i, j}=\left(f_{i}-g_{j}\right)^{2} $ | (8) |
式中:ei,j为误差矩阵E的第i行,第j列元素。
第2步,计算误差累积矩阵C ∈ RM×N
| $ \left\{\begin{array}{l}{c_{1, 1}=e_{1, 1}} \\ {c_{1, j}=c_{1, j-1}+e_{1, j}} \\ {c_{j, 1}=c_{j-1, 1}+e_{j, 1}} \\ {c_{i, j}=\min \left(c_{i, j-1}, c_{i-1, j}, c_{i-1, j-1}\right) \quad i \neq 1, j \neq 1}\end{array}\right. $ | (9) |
第3步,通过C,计算出累积误差最小的规整路径u,并同时满足3个约束条件:①边界条件:u1 = (1,1)和uL =(M,N),要求规整路径分别以c1,1和cM,N为起点和终点;②单调条件:规整路径的纵横坐标均是单调不减的,即当相邻2个点为ui =(a,b)和ui-1=(a',b'),则满足a-a' ≥ 0和b-b' ≥ 0;③连续性条件:规整路径中相邻2点必须是C中的相邻点格,当相邻2个点为ui =(a,b)和ui-1=(a',b'),则满足a-a' ≤ 1和b-b' ≤ 1,即保证f和g的每一个坐标都会在u中出现。
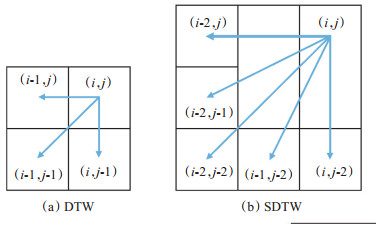
第4步,计算流程第2步中所构建累积误差矩阵相当于逐点搜索3种可能斜率(-1,0和1)的局部规整路径,但估计出的规整路径不够精确和平滑,与实际地震资料不符。SDTW将该步骤改为间隔h点搜索2h + 1种可能斜率(斜率范围为-1~ 1)的局部路径,计算出一个粗网格的累积误差矩阵,这2种方法构建累积误差矩阵对比如图 1所示,其中图 1(a)为传统方法搜索3种可能的局部路径,图 1(b)以h = 2为例,说明SDTW搜索2h + 1种可能斜率的局部路径,所构造出的规整路径精确度必然提高。
|
下载eps/tif图 图 1 累积误差矩阵构建方法对比 Fig. 1 Comparison of construction methods of cumulative error matrix |
叠前道集剩余时差校正方法假设:①地下地层为层状介质,各层介质均为均匀、各向同性弹性介质;②地震正演满足褶积模型(Robison模型),表示为
| $ \mathit{\boldsymbol{s}}{\rm{ = }}\mathit{\boldsymbol{W x}}{\rm{ + }}\mathit{\boldsymbol{n}} $ | (10) |
式中:s为地震记录;W为子波核矩阵;x为反射系数序列;n为噪声。③叠前道集中各道信号反映相同的地下地层信息,因而具有相干性,从信号与系统的角度看,地震地质模型等价于一个线性时不变系统,输入为子波,输出为地震记录,反射系数表达了层状地质模型。鉴于褶积模型的精度和采集误差,将x看作地层系统的单位冲击响应更为合适。
褶积模型[式(10)]和稀疏表示数学模型[式(1)]具有相同的数学形式,其计算流程如下:
(1) 利用地震子波构造过完备字典。随着油气勘探和开发工作的不断深入发展,薄层储层预测已经成为一个研究热点和难点问题,由于地层厚度薄,薄层的顶、底面常互相干涉叠加,从式(10)中难以精确反演出地下地层的单位冲击响应。针对这一问题,采用Zhang等[23]提出的过完备子波字典构造方法,薄层顶、底面的单位冲激响应构成一个薄层反射,通过双极子分解可以将其分解为一个偶序列和一个奇序列之和,其中奇序列具有更高的分辨率,通过将不同深度、不同厚度的薄层反射分解为一系列奇分量序列和偶分量序列,再与地震子波褶积就能构造出过完备字典。
(2) 采用SBL对地震道集进行稀疏表示,构造出系数矩阵,相当于地下介质的单位冲击响应,消除了子波影响。
(3) 利用DTW对系数矩阵进行剩余时差校正,就能避免直接使用DTW对地震道进行处理造成的波形畸变。
(4) 用校正后系数矩阵重构地震记录。
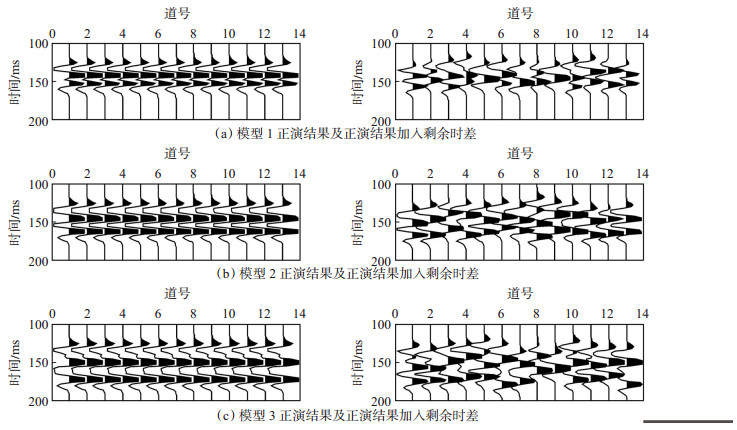
2 数值模拟为了验证联合SBL和DTW的叠前道集剩余时差校正技术的有效性,建立3组不同层厚的4层地质模型,模型参数如表 1所列。3组模型均采用30 Hz雷克子波进行地震正演,无剩余时差地震记录,由于剩余时差常由速度误差引起,通过对模型地层速度加入随机误差来模拟剩余时差,剩余时差不仅引起同相轴时间深度差异,还会造成波形畸变(图 2)。
|
|
下载CSV 表 1 模型参数 Table 1 Model parameters |
|
下载eps/tif图 图 2 地质模型正演结果 Fig. 2 Forward modeling of geological models |
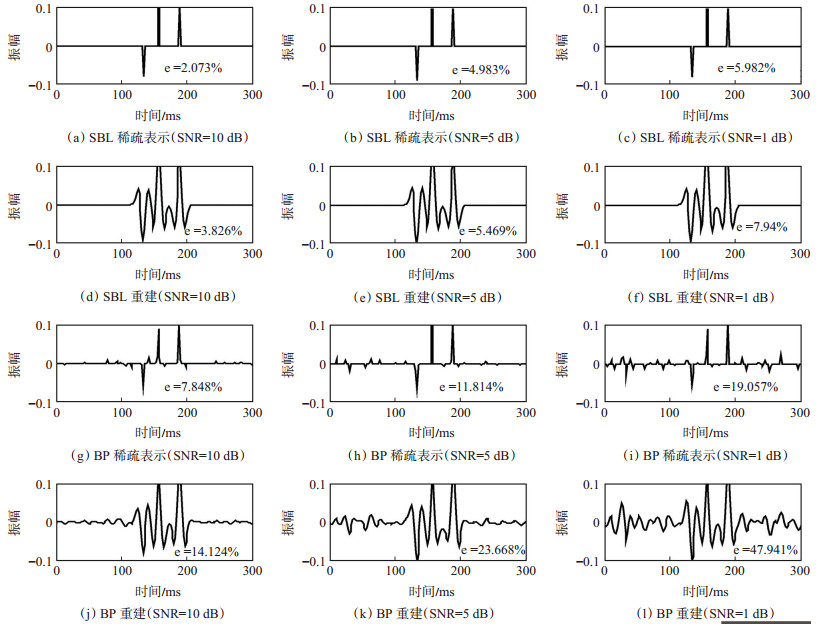
对模型3第1道加入不同强度的随机噪声,对比SBL和BP这2种算法稀疏表示精度和重建精度(图 3),图 3中从上向下,噪声信号的信噪比(Signal to Noise Ratio,SNR)分别为10 dB,5 dB,1 dB,结果显示SBL计算出的系数向量具有较好的脉冲性,与地层单位冲击响应特征吻合[图 3(a)-(c)]。SBL重建地震波形曲线光滑,消除了噪声干扰[图 3 (d)-(f)],强噪声条件下(SNR = 1 dB),仍然能够达到较高的重建精度[图 3(f)]。BP算法对噪声敏感,计算出的系数向量中存在较多毛刺,与实际数据误差较大[图 3(g)-(i)]。BP重建地震记录与SBL算法相比误差较大[图 3(k)-(m)]。随着噪声变强,SNR逐渐降低,2种算法的稀疏表示精度和重建精度均有所降低,但SBL算法2种相对误差均小于BP算法,在强噪声条件下,BP算法2种相对误差分别达到了19.057%和47.941%,而SBL算法仅为于5.982%和7.940%,远低于BP算法,可见SBL算法具有明显的计算精度,用于地震数据稀疏表示是有效的。
|
下载eps/tif图 图 3 SBL与BP稀疏表示及重建精度对比 Fig. 3 Comparison of sparse representation and reconstruction accuracy of SBL and BP |
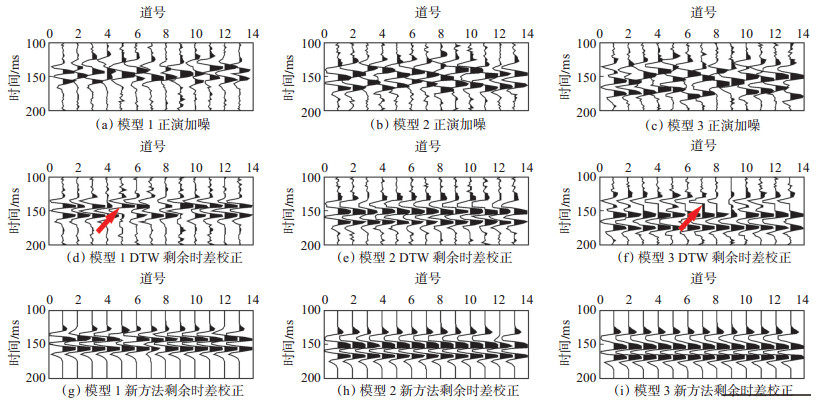
联合SBL和DTW算法(新方法)的优势是同时实现了高精度剩余时差校正和随机噪声压制。在SNR = 1 dB条件下,将新方法与DTW算法[3]的处理效果进行对比(图 4),DTW算法对模型2应用效果良好[图 4(e)],而模型1由于地层较薄,速度误差会使波形干涉叠加,DTW不能使叠加波形解调[图 4(d)中箭头所示],模型3中,上下2个同相轴存在互相干涉,DTW剩余时差校正算法使同相轴产生畸变[图 4(f)中箭头所示],而联合SBL和DTW的新算法能够使互相干涉的同相轴解调,剩余时差校正效果良好,波形畸变远小于DTW[图 4(g)- (i)]。由此可知,DTW适用于厚地层剩余时差校正,薄地层应用效果较差,并且容易产生波形畸变,新方法实现剩余时差校正的同时压制了地震噪声。
|
下载eps/tif图 图 4 低噪声(SNR=10 dB)条件下新算法与DTW算法处理效果对比分析 Fig. 4 Comparative analysis of processing results of two residual moveout correction algorithms under high SNR(SNR = 10 dB) |
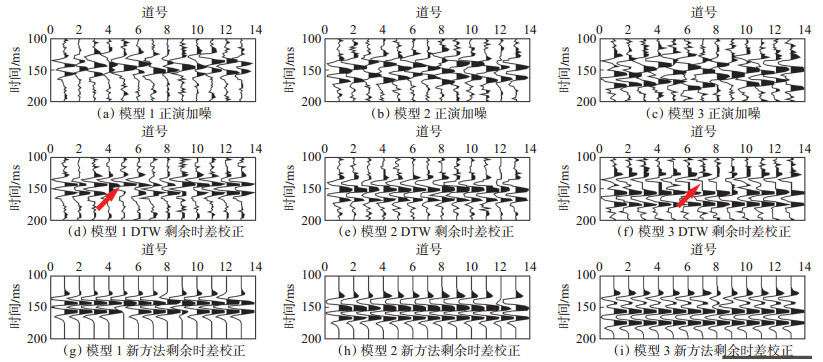
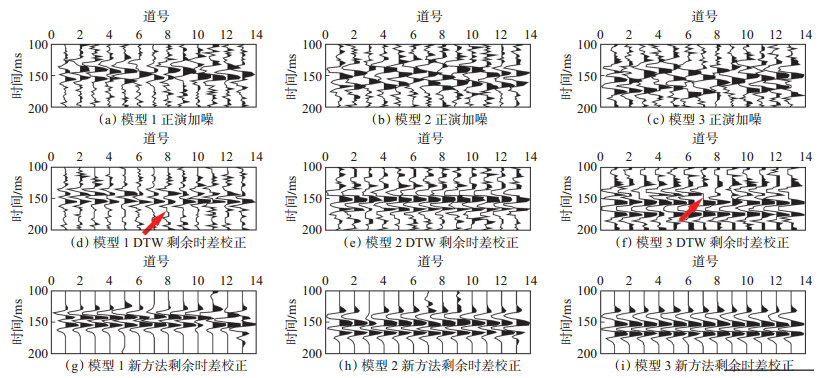
在SNR = 5 dB和SNR = 1 dB条件下能够得到同样的结论。同时,噪声强度增加,信噪比降低,2种算法处理效果都会变差,DTW处理结果产生明显畸变(图 5,图 6中箭头所示)。强噪声条件下,DTW处理结果噪声干扰严重,同相轴被噪声淹没,识别困难,而新算法具有明显的去噪能力,强噪声条件下仍然能够得到高信噪比处理结果,处理后剩余时差得到校正,且同相轴畸变不明显。由此可知,结合SBL和DTW的剩余时差校正方法对不同品质的地震资料都是有效的。
|
下载eps/tif图 图 5 中等噪声(SNR = 5 dB)条件下新算法与DTW算法处理效果对比分析 Fig. 5 Comparative analysis of processing results of two residual moveout correction algorithms under moderate noise contaminated(SNR = 5 dB) |
|
下载eps/tif图 图 6 强噪声(SNR = 1 dB)条件下新算法与DTW算法处理效果对比分析 Fig. 6 Comparative analysis of processing results of two residual moveout correction algorithms under trong noise contaminated(SNR = 1 dB) |
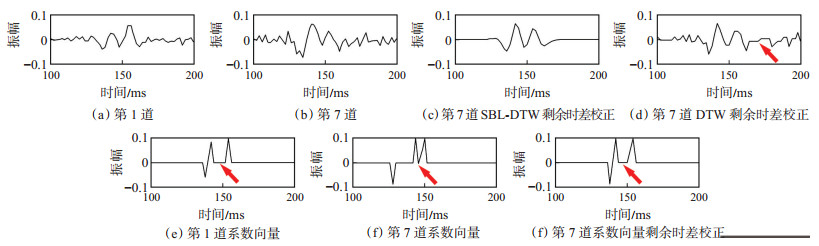
为了说明联合SBL和DTW的剩余时差校正方法的原理,进一步验证算法的有效性,以模型1第8道为例,对比分析强噪声(SNR = 1 dB)条件下2种算法处理结果(图 7)。取2个强噪声污染地震信号,以第1道[图 7(a)]作为参考道,对第7道[图 7(b)]用新算法和DTW算法分别进行剩余时差校正。单独使用DTW算法对原始地震道进行剩余时差校正处理后仍然存在明显的波形畸变[图 7(d)中箭头所示]。
|
下载eps/tif图 图 7 模型1第8道新算法与DTW算法处理结果对比分析 Fig. 7 Comparative analysis of processing results of two algorithms in the 8th trace of model 1 |
采用新方法,先对地震道进行稀疏表示,由于存在剩余时差,同一地层的单位冲击响应存在明显的时差[图 7(e)—(f)中箭头所示],再对稀疏表示结果[图 7(f)]作DTW剩余时差校正[图 7(g)],地层单位冲击响应校正到正确位置,由处理后的系数向量重构地震道[图 7(c)],剩余时差得到校正,地震波形没有发生明显的畸变。
3 应用实例为了验证联合SBL和DTW的叠前道集剩余时差校正方法的有效性,以加拿大Nova Scotia省的Penobscot工区(数据由dGB Earth Sciences提供)为例进行试算。研究区位于Scotian盆地Abenaki凹陷与Sable凹陷的过渡带,主力储层为侏罗系上统Abenaki组。工区面积88.6 km2,包括600条主测线和481条联络测线,地震面元为12.5 m×25.0 m,60次覆盖,4 ms采样,记录长度为6 000 ms。
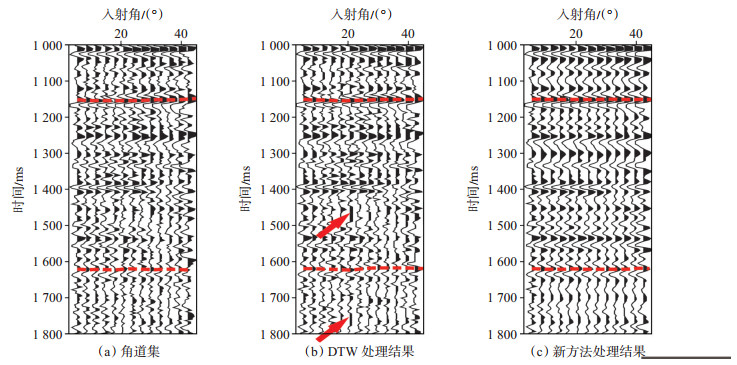
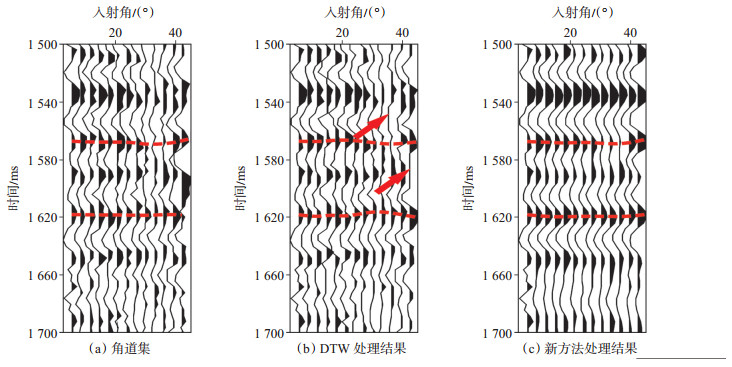
原始共中心点角道集,资料噪声干扰严重,同相轴连续性差,受资料品质影响,前期地震数据处理不能拉平同相轴,处理后数据存在明显剩余时差,如图 8(a),图 9(a)中虚线标注的同相轴所示,其中图 9为图 8在1.5~1.7 s部分的放大图。经DTW处理后,剩余时差得到部分校正,但同相轴仍未校平,受DTW算法制约,校正后角道集中存在明显的波形畸变[图 8(b),图 9(b)中箭头所示]。结合SBL和DTW的新算法处理后剩余时差得到校正,同相轴拉平,同相轴连续性得到增强[图 8(c),图 9(c)中虚线所示],同时噪声得到压制,提高了地震资料信噪比,利用这一方法处理后的地震数据进行叠前反演、AVO分析等处理流程,其结果的精度和可信度也得以提高。
|
下载eps/tif图 图 8 Penobscot工区新算法与DTW算法处理效果对比分析 Fig. 8 Comparative analysis of processing results of two residual moveout correction algorithms in Penobscot project |
|
下载eps/tif图 图 9 工区新算法与DTW算法处理效果对比局部放大显示 Fig. 9 Zoom-in of angle gathers contrast before and after residual moveout correction in Penobscot project |
(1) 受地震资料品质和处理方法的制约,处理后地震资料常存在剩余时差,提出一种联合SBL和DTW的叠前道集剩余时差校正方法,能够同时实现噪声压制和剩余时差校正,处理后叠前道集同相轴被拉平,连续性得到增强,满足叠前反演、AVO分析等流程对资料品质要求。
(2) DTW算法采用逐点搬家的方法进行时差校正,容易引起波形畸变,在DTW时差校正前,利用SBL对地震数据进行稀疏表示,其结果相当于地下介质的单位冲击响应,能够消除地震子波影响,再对计算出的系数矩阵进行剩余时差校正和重建计算,就能够避免波形发生畸变。
(3) SBL算法能够适用于高相干度字典,适用于地震数据稀疏表示,SBL算法的计算效率是限制其应用于大规模地震数据剩余时差校正的瓶颈,可采用压缩感知对地震数据进行随机采样,降低处理方法的计算量。
| [1] |
刘振峰. 油气地震地质模型述评. 岩性油气藏, 2018, 30(1): 19-29. LIU Z F. Review on oil and gas seismogeology models. Lithologic Reservoirs, 2018, 30(1): 19-29. DOI:10.3969/j.issn.1673-8926.2018.01.002 |
| [2] |
陈可洋. 逆时成像技术在大庆探区复杂构造成像中的应用. 岩性油气藏, 2017, 29(6): 91-100. CHEN K Y. Application of reverse-time migration technology to complex structural imaging in Daqing exploration area. Lithologic Reservoirs, 2017, 29(6): 91-100. DOI:10.3969/j.issn.1673-8926.2017.06.012 |
| [3] |
曲寿利. AVO分析中的剩余时差校正. 石油地球物理勘探, 1991, 26(4): 523-528. QU S L. Residual moveout correction in AVO analysis. Oil Geophysical Prospecting, 1991, 26(4): 523-528. |
| [4] |
周鹏, 刘志斌, 张益明, 等. 动校剩余时差处理方法及应用. 地球物理学进展, 2015, 30(5): 2349-2353. ZHOU P, LIU Z B, ZHANG Y M, et al. The processing method and application of the residual moveout NMO. Progress in Geophysics, 2015, 30(5): 2349-2353. |
| [5] |
石战战, 唐湘蓉, 庞溯, 等. 一种基于SC-DTW的叠前道集剩余时差校正方法. 岩性油气藏, 2017, 29(5): 113-119. SHI Z Z, TANG X R, PANG S, et al. Prestack gather residual moveout correction based on shape context and dynamic time warping. Lithologic Reservoirs, 2017, 29(5): 113-119. DOI:10.3969/j.issn.1673-8926.2017.05.013 |
| [6] |
TIPPING M E. Sparse Bayesian learning and the relevance vector machine. Journal of Machine Learning Research, 2001, 1(3): 211-244. |
| [7] |
MALLAT S G, ZHANG Z. Matching pursuits with time-frequency dictionaries. IEEE Trans on Signal Processing, 1993, 41(12): 3397-3415. DOI:10.1109/78.258082 |
| [8] |
陈胜, 欧阳永林, 曾庆才, 等. 匹配追踪子波分解重构技术在气层检测中的应用. 岩性油气藏, 2014, 26(6): 111-114. CHEN S, OUYANG Y L, ZENG Q C, et al. Application of matching pursuit wavelet decomposition and reconstruction technique to reservoir prediction and gas detection. Lithologic Reservoirs, 2014, 26(6): 111-114. DOI:10.3969/j.issn.1673-8926.2014.06.018 |
| [9] |
CHEN S S, DONOHO D L, SAUNDERS M A. Atomic decomposition by basis pursuit. Siam Review, 2001, 43(1): 129-159. DOI:10.1137/S003614450037906X |
| [10] |
WIPF D P, RAO B D. Sparse Bayesian learning for basis selection. IEEE Transactions on Signal Processing, 2004, 52(8): 2153-2164. DOI:10.1109/TSP.2004.831016 |
| [11] |
WIPF D P, RAO B D. An empirical Bayesian strategy for solving the simultaneous sparse approximation problem. IEEE Transactions on Signal Processing, 2007, 55(7): 3704-3716. DOI:10.1109/TSP.2007.894265 |
| [12] |
ZHANG Z, RAO B D. Sparse signal recovery with temporally correlated source vectors using sparse Bayesian learning. IEEE Journal of Selected Topics in Signal Processing, 2011, 5(5): 912-926. DOI:10.1109/JSTSP.2011.2159773 |
| [13] |
ZHANG Z, RAO B D. Extension of SBL algorithms for the recovery of block sparse signals with intra-block correlation. IEEE Transactions on Signal Processing, 2013, 61(8): 2009-2015. DOI:10.1109/TSP.2013.2241055 |
| [14] |
ZHANG Z, RAO B D. Exploiting correlation in sparse signal recovery problems: Multiple measurement vectors, block sparsity, and time-varying sparsity. ICML 2011 Workshop on Structured Sparsity: Learning and Inference. Bellevue: International Machine Learning Society, 2011.
|
| [15] |
RAO B D, ZHANG Z, JIN Y. Sparse signal recovery in the presence of intra-vector and inter-vector correlation. International Conference on Signal Processing and Communications. Bangalore: Indian Institute of Science, 2012.
|
| [16] |
YI B K, JAGADISH H V, FALOUTSOS C. Efficient retrieval of similar time sequences under time warping. Fourteenth International Conference on Data Engineering. Orlando: IEEE Computer Society, 1998.
|
| [17] |
KIM S W, PARK S, CHU W W. An index-based approach for similarity search supporting time warping in large sequence databases. Seventeenth International Conference on Data Engineering. Heidelberg: IEEE Computer Society, 2001.
|
| [18] |
KEOGH E, RATANAMAHATANA C A. Exact indexing of dynamic time warping. Knowledge & Information Systems, 2005, 7(3): 358-386. |
| [19] |
LEMIRE D. Faster retrieval with a two-pass dynamic-timewarping lower bound. Pattern Recognition, 2009, 42(9): 2169-2180. DOI:10.1016/j.patcog.2008.11.030 |
| [20] |
AL-NAYMAT G, CHAWLA S, TAHERI J. Sparse DTW: a novel approach to speed up dynamic time warping. Eighth Australasian Data Mining Conference. Melbourne: Australian Computer Society, 2009.
|
| [21] |
COMPTON S, HALE D. Estimating vp/vs ratios using smooth dynamic image warping. Geophysics, 2014, 79(6): 1639-1643. |
| [22] |
CUI T. Improving seismic-to-well ties. Calgary: University of Calgary, 2015.
|
| [23] |
ZHANG R, CASTAGNA J. Seismic sparse-layer reflectivity inversion using basis pursuit decomposition. Geophysics, 2011, 76(6): R147-R158. DOI:10.1190/geo2011-0103.1 |
 2019, Vol. 31
2019, Vol. 31



