2. 西安石油大学 电子工程学院, 西安 710065;
3. 西安石油大学陕西省油气井及储层渗流与岩石力学重点实验室, 西安 710065;
4. 西安石油大学 石油工程学院, 西安 710065;
5. 川庆钻探土库曼斯坦分公司 质量安全环保科, 西安 710051;
6. 西安地质调查中心, 西安 710054
2. School of Electronic Engineering, Xi'an Shiyou University, Xi'an, 710065, China;
3. The Key Laboratory of Well Stability and Fluid & Rock Mechanics in Oil and Gas Reservoir of Shaanxi Province, Xi'an Shiyou University, Xi'an 710065;
4. School of Petroleum Engineering, Xi'an Shiyou University, Xi'an 710065, China;
5. Quality Safety and Environmental Protection Section, Chuanqing Drilling Turkmenistan Branch, Xi'an 710051, China;
6. Xi'an Center of Geological Survey, Xi'an 710054, China
由于泥页岩中黏土矿物特殊的物理化学性质,当泥浆中水的活度大于地层水活度时,泥浆中的水分会向井壁渗透,致使泥页岩吸水发生膨胀或裂解;反之,地层水会向井内渗流致使泥页岩脱水进而强度发生改变,两者都不利于井壁稳定,但泥页岩吸水对其稳定性的影响更大[1-2]。由于泥页岩地层存在水化现象[3-4],一方面降低了岩石的力学强度[5],另一方面水化作用会产生膨胀应力,增加岩石的孔隙压力[6-7],使岩石力学强度减小。此外,由于钻井液及其滤液向地层渗流,在井周形成渗流附加应力场[8-9],导致井周有效周向应力降低,进而对泥页岩破裂压力产生很大的影响[10]。
国内外学者提出了许多预测破裂压力的模型和方法,各有优缺点。Eaton模型[11]考虑了上覆压力引起的水平应力总量和泊松比的函数关系;Anderson [12]在Eaton模型的基础上引入了多孔介质弹性系数,利用测井资料计算破裂压力;Dasgupta等[13]应用地层的压实曲线计算了Eaton模型中参数的关系进而求得破裂压力;Ma等[14-15]研究了层状岩体各向异性抗拉强度的特征,推导了3种不同各向异性破坏准则的断裂压力模型。以上模型的参数选取均会受到主观经验的影响。黄荣樽[9, 16]提出的黄氏模型不仅考虑了岩层上覆应力与深度的关系和井壁应力集中的影响,而且还考虑到地下非均匀分布的构造应力的作用以及岩层抗张强度等因素,因此,它能适用于不同条件的地区,所预测的破裂压力较其他模式更为准确可靠,然而,该模型没有考虑岩石孔隙度、渗流和水化作用的影响。严向阳等[17]在黄氏模型的基础上建立了考虑水化应力计算破裂压力的模型,提高了预测精度,但是该模型没有考虑射孔孔眼以及天然裂缝对水力裂缝的起裂影响,因此该模型只适合于预测裸眼直井情况下的沿岩石本体破裂的压力预测。邓金根等[18]建立了综合考虑温度及渗流影响的高温高压地层破裂压力计算新模型,预测精度提高了7%,但是此模型中的井壁温度(除了某一井段)变化对破裂压力的影响不大,而且主要针对的地层是砂岩,没有考虑水化作用的影响。东振等[19]运用断裂力学理论推导裂缝性地层破裂压力计算公式,结合分形岩石力学理论建立裂缝性地层破裂压力解析模型,提出了一种实用的破裂压力计算方法,但主要是针对煤岩。李传亮[20]建立了射孔完井条件下的破裂压力计算模型,然而怎样获取连续的触点孔隙度参数剖面,还是个尚未解决的问题。李培超[21]对李传亮的射孔完井破裂压力模型进行了修正,引入射孔深度参数,最终得到垂直井射孔完井破裂压力计算公式,但仅考虑了钻井引起的应力集中,忽视了射孔引起的二次应力集中对破裂压力的影响。
泥页岩的水敏性是不容忽视的问题,本文在黄氏模型的基础上,结合泥页岩水化和渗流特征,建立泥页岩地层破裂压力计算新模型,并计算泥页岩地层破裂压力和含水率的关系,以期得到更加准确的地层破裂压力,为工程设计和压裂方案制定提供理论基础。
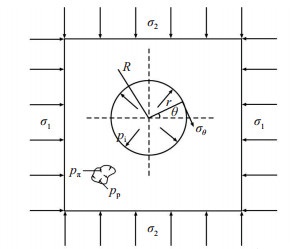
1 泥页岩破裂压力模型的推导在无限大平面上,一个圆孔受到均匀的内压,同时在这个平面上的无限远处受到2个水平地应力的作用,其垂直方向上受到上覆压力。考虑到岩石为小变形弹性体,可以适用线性叠加原理。井壁围岩的应力状态可通过先研究各应力分量对井壁围岩的应力贡献,而后进行叠加的方法获得。假设地层是均匀各向同性、线弹性多孔材料,并认为井眼周围的岩石处于平面应变状态[1]。井壁受力模型如图 1所示。
|
下载eps/tif图 图 1 井眼周围受力状态 Fig. 1 Stress state around well |
视井壁围岩为多孔介质,其中的流体流动满足达西定律,则钻井液滤液在地层中的径向渗流在井壁围岩会产生附加应力场,联合钻井液液柱压力和地应力的作用,垂直井井壁周围地层的周向应力分布[2]为
| $ {\sigma _\theta } = - \frac{{{R^2}}}{{{r^2}}}{p_{\rm{i}}} + \frac{{{\sigma _1} + {\sigma _2}}}{2}\left( {1 + \frac{{{R^2}}}{{{r^2}}}} \right) - \frac{{{\sigma _1} - {\sigma _2}}}{2}\left( {1 + \frac{{3{R^4}}}{{{r^4}}}} \right)\cos 2\theta + \delta \left[ {\frac{{\alpha '\left( {1 - 2\mu } \right)}}{{2\left( {1 - \mu } \right)}}\left( {1 + \frac{{{R^2}}}{{{r^2}}}} \right) - \mathit{\Phi }} \right]\left( {{p_{\rm{i}}} - {p_{\rm{p}}}} \right) $ | (1) |
式中:σθ 为周向应力,MPa;pi为钻井液液柱压力,MPa;pp为原始地层的孔隙压力,MPa;α'为有效应力系数;μ为泊松比;σ1为水平最大地应力,MPa;σ2为水平最小地应力,MPa;R为最大井眼半径,m;r 为井眼半径,m;δ为渗透系数;Φ为泥页岩孔隙度;θ为径向上最大地应力方向逆时针旋转的极坐标角,(°)。
当井壁可渗透时,δ = 1。当r = R时,井壁表面上的周向应力为
| $ \begin{array}{l} {\sigma _\theta } = - {p_{\rm{i}}} + \left( {1 - 2\cos 2\theta } \right){\sigma _1} + \left( {1 + 2\cos 2\theta } \right){\sigma _2} + \\ \;\;\;\;\;\;\;\delta \left[ {\frac{{\alpha '\left( {1 - 2\mu } \right)}}{{2\left( {1 - \mu } \right)}} - \mathit{\Phi }} \right]\left( {{p_{\rm{i}}} - {p_{\rm{p}}}} \right) \end{array} $ | (2) |
井内液体所产生的地层裂缝多为垂直的,这是由于周向应力从压缩变为拉伸时超过了岩层的抗拉强度所造成的。当θ = 0°和180°时,σθ 值最小为
| $ {\sigma _\theta } = 2{\sigma _2} - {\sigma _1} - {p_{\rm{i}}} + \left[ {\frac{{\alpha '\left( {1 - 2\mu } \right)}}{{2\left( {1 - \mu } \right)}} - \mathit{\Phi }} \right]\left( {{p_{\rm{i}}} - {p_{\rm{p}}}} \right) $ | (3) |
当采用水基钻井液钻井遇到泥页岩时,在水力压差、化学势差以及包括钻井液液柱压力与孔隙压力之间的压力差作用下,水分子会侵入裂隙及颗粒之间的孔隙,引起水和离子的传递,然后进入岩石微裂纹,发生水化作用[4]。在一定条件下,可以把井壁当作半渗透膜,其两边为钻井液体系和地层孔隙流体体系。在此基础上,Chenevert等[23]提出了计算模型来表述水化应力,将其当成静水压力来处理,计算公式为
| $ {p_{\rm{ \mathit{ π} }}} = {I_{\rm{m}}}\frac{{R'T}}{{\bar V}}\ln \frac{{{{\left( {{A_{\rm{w}}}} \right)}_{\rm{m}}}}}{{{{\left( {{A_{\rm{w}}}} \right)}_{{\rm{sh}}}}}} \times {10^{ - 6}} $ | (4) |
式中:pπ为水化应力,MPa,Im为透膜效率;R'为气体常数;T为绝对温度,K;V为纯水偏摩尔体积;m3·mol-1,(Aw)m为进入地层的液体活度;(Aw)sh为泥页岩中水的活度。
假定大多数泥页岩的结构能使孔隙中的流体在孔隙中流通,形成一致的孔隙压力传给岩石的骨架,那么有效应力等于正应力减去孔隙压力和水化应力。因此有效周向应力便为
| $ \begin{array}{l} {{\sigma '}_\theta } = 3{\sigma _2} - {\sigma _1} - {p_{\rm{i}}} + \left[ {\frac{{\alpha '\left( {1 - 2\mu } \right)}}{{2\left( {1 - \mu } \right)}} - \mathit{\Phi }} \right]\left( {{p_{\rm{i}}} - {p_{\rm{p}}}} \right) - \\ \;\;\;\;\;\;\;{p_{\rm{p}}} - {p_{\rm{ \mathit{ π} }}} \end{array} $ | (5) |
根据最大张应力准则,地层产生破裂的条件为
| $ {{\sigma '}_\theta } = - {S_{\rm{t}}} $ | (6) |
式中:St为岩石的抗张强度,MPa。达到这个条件时的pi便为破裂压力pF。
令
| $ {p_{\rm{F}}} = \frac{1}{{1 - K}}\left[ {3{\sigma _2} - {\sigma _1} + {S_{\rm{t}}} - \left( {1 + K} \right){p_{\rm{p}}} - {p_{\rm{ \mathit{ π} }}}} \right] $ | (7) |
式中:pF为地层破裂压力,MPa。
作用在垂直方向上的主地应力称为上覆应力σ3,是由上覆岩层的重力产生的,其随着岩层的深度而变化。有效上覆应力σ'3为
| $ {{\sigma '}_3} = {\sigma _3} - {p_{\rm{p}}} $ | (8) |
根据文献[6],在有构造应力时,一般情况下在2个水平主应力方向上所附加的有效应力是不相等的,分别为
| $ {{\sigma '}_1} = \frac{\mu }{{1 - \mu }}{{\sigma '}_3} + \alpha {{\sigma '}_3} + {p_{\rm{p}}}, {{\sigma '}_2} = \frac{\mu }{{1 - \mu }}{{\sigma '}_3} + \beta {{\sigma '}_3} + {p_{\rm{p}}} $ | (9) |
式中:σ'1为最大水平有效应力,MPa;σ'2为最小水平有效应力,MPa;α,β均为地质构造应力系数。
把式(9)代入式(7)中,便可得到泥页岩地层破裂压力的公式:
| $ {p_{\rm{F}}} = \frac{1}{{1 - K}}\left( {{S_{\rm{t}}} - {p_{\rm{ \mathit{ π} }}}} \right) + {p_{\rm{p}}} + \frac{1}{{1 - K}}\left( {\frac{{2\mu }}{{1 - \mu }} + 3\beta - \alpha } \right){{\sigma '}_3} $ | (10) |
根据长庆油田泥页岩地层岩心水化三轴压缩实验[4-5]、泥页岩孔隙度的测量[24]、渗透率实验[24],得到泥页岩地层岩石的基本参数如表 1所列。
|
|
下载CSV 表 1 长庆油田泥页岩地层常规参数 Table 1 Conventional parameters of shale formation in Changqing Oilfield |
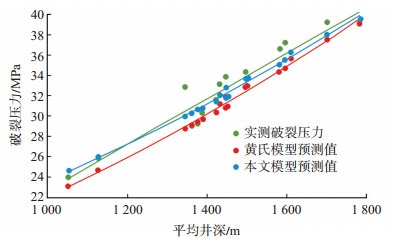
根据长庆油田实测地层压裂实验的数据[16],将表 1中的泥页岩岩石参数代入公式(10)中,计算得本文模型预测的破裂压力(表 2),并将本文模型和黄氏模型预测值与实测破裂压力进行对比(图 2)。
|
下载eps/tif图 图 2 2种模型预测值与实测破裂压力对比 Fig. 2 Comparisons between predicted values of two models and the measured fracture pressu |
|
|
下载CSV 表 2 长庆油田油层部位地应力和预测破裂压力值 Table 2 Crustal stress and predicted fracture pressures of reservoir in Changqing Oilfield |
从图 2可以看出,本文模型预测值比黄氏模型高一些,更加接近实测破裂压力。由此可以计算出黄氏模型的预测误差为4.95%,本文模型的预测误差为3.65%。本文模型的预测值与实际地层破裂压力梯度的符合性更高,由此计算得到的当量钻井液密度更符合实际。这是由于当对泥页岩地层进行水力压裂时,钻井液或压裂液渗入泥页岩地层,使泥页岩地层发生水化作用而产生水化应力,再加上钻井液或者压裂液渗流造成的附加应力场,造成井壁围岩应力的增加,进而致使破裂压力增加。
3 含水率与泥页岩破裂压力的关系根据屈展等[2]在不同浸泡时间下进行的不同含水率下泥页岩岩心的三轴压缩实验,得到泥页岩在不同含水率下的抗压强度。根据Guo等[26]得出的泥页岩抗张强度约为其抗压强度的1/15~1/8的结论,可以计算出泥页岩地层岩心在不同含水率下的抗张强度(表 3)。
|
|
下载CSV 表 3 泥页岩在不同含水率下的抗张强度 Table 3 Tensile strength of shale under different water contents |
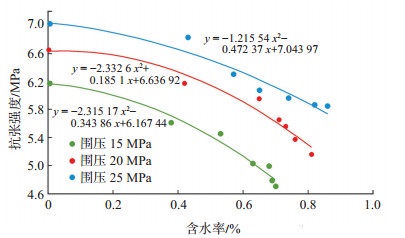
根据表 3 数据拟合出抗张强度和含水率的关 系曲线 (图 3)
|
下载eps/tif图 图 3 泥页岩在不同含水率下的抗张强度 Fig. 3 Tensile strength of shale under different water contents |
从图 3可以看出,在不同的围压作用下,抗张强度均随着含水率的升高而降低。这是因为泥页岩黏土类矿物质含量较高以及微裂纹发育较好时,钻井液与其接触,黏土矿物极易吸水膨胀,还会发生水化作用,致使泥页岩岩石孔隙增大,内部结构变得更加松散,微裂纹扩展,进而降低了岩石的力学性能。
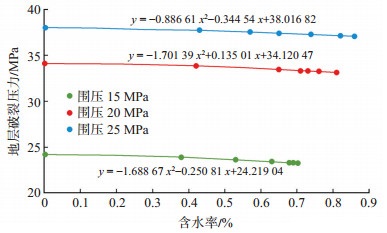
把不同围压下的抗张强度和含水率的拟合关系代入本文模型中,得到不同含水率下的泥页岩地层的破裂压力(图 4)。
|
下载eps/tif图 图 4 不同含水率下泥页岩地层破裂压力 Fig. 4 Fracture pressure of shale formation at different water contents |
从图 4可以看出,不同围压下的泥页岩地层破裂压力均随着含水率的升高,呈下降趋势,表明水化作用和渗流对泥页岩破裂压力的影响非常显著。
这是因为泥页岩与钻井液之间存在耦合流动,驱动因素就是水力压差、化学势、钻井液液柱压力和岩石中的孔隙压力的压力差,在其作用下,钻井液和压裂液进入泥页岩地层,泥页岩中存在的大量黏土矿物,遇水会产生水化膨胀现象,水化作用改变了泥页岩的岩石力学性质,致使泥页岩的抗压强度随着含水率的升高而降低,泥页岩的抗张强度也随着含水率的升高而降低,进而可以得出泥页岩地层破裂压力随着含水率的升高而降低。
4 结论(1)结合弹塑性力学和岩石力学相关理论,应用最大张应力准则,建立了泥页岩破裂压力的预测模型,在黄氏模型的基础上考虑了钻井渗滤液在地层孔隙中的径向渗流而在井壁围岩所产生的附加应力场,岩石的孔隙度和钻井液水化作用的影响,理论模型计算误差为3.65%,与实测结果比较接近,提高了计算精度。
(2)在不同的围压作用下,抗张强度均随着含水率的升高而降低。这是因为泥页岩中黏土类矿物质以及微裂纹与钻井液接触发生水化作用,致使岩石孔隙增大,内部结构变得更加松散,微裂纹扩展,进而降低了岩石的力学性能。
(3)破裂压力随着含水率的升高呈下降趋势。随着含水率的提高,水软化岩石,致使泥页岩的抗压强度和抗张强度均减小,导致破裂压力降低。
| [1] |
刘向君, 罗平亚. 泥岩地层井壁稳定性研究. 天然气工业, 1997, 17(1): 45-48. LIU X J, LUO P Y. Study on the stability of well wall in mudstone strata. Natural Gas Industry, 1997, 17(1): 45-48. |
| [2] |
屈展, 王萍. 泥页岩井壁蠕变损伤失稳研究. 北京: 科学出版社, 2016: 10. QU Z, WANG P. Creep damage instability study of shale. Beijing: Science Press, 2016: 10. |
| [3] |
张莹莹, 黄思静. 华庆地区长6油层组方解石胶结物特征. 岩性油气藏, 2012, 24(2): 48-52. ZHANG Y Y, HUANG S J. Characteristics of calcite cements of Chang 6 oil reservoir set in Huaqing area. Lithologic Reservoirs, 2012, 24(2): 48-52. DOI:10.3969/j.issn.1673-8926.2012.02.010 |
| [4] |
王萍, 屈展, 黄海, 等. 含水状态下硬脆性泥页岩蠕变特性实验研究. 科学技术与工程, 2016, 16(15): 66-71. WANG P, QU Z, HUANG H, et al. Creep experimental study of brittle shale triaxial state under aqueous. Science Technology & Engineering, 2016, 16(15): 66-71. DOI:10.3969/j.issn.1671-1815.2016.15.011 |
| [5] |
王萍, 屈展, 黄海. 地层水矿化度对硬脆性泥页岩蠕变规律影响的试验研究. 石油钻探技术, 2015, 43(5): 63-68. WANG P, QU Z, HUANG H. Experimental study of the effect of formation water salinity on creep laws of the hard-brittle shale. Petroleum Drilling Techniques, 2015, 43(5): 63-68. |
| [6] |
张洪, 孟选刚, 邵长金, 等. 水平压裂裂缝形成机理及监测:以七里村油田为例. 岩性油气藏, 2018, 30(5): 138-145. ZHANG H, MENG X G, SHAO C J, et al. Forming mechanism and monitoring of horizontal hydraulic fracture:a case from Qilicun oilfield. Lithologic Reservoirs, 2018, 30(5): 138-145. |
| [7] |
马飞英, 王永清, 王林, 等. 煤岩中水分含量对渗透率的影响. 岩性油气藏, 2013, 25(3): 97-101. MA F Y, WANG Y Q, WANG L, et al. Influence of moisture content in coal rock on permeability. Lithologic Reservoirs, 2013, 25(3): 97-101. DOI:10.3969/j.issn.1673-8926.2013.03.017 |
| [8] |
张烈辉, 单保超, 赵玉龙, 等. 页岩气藏表观渗透率和综合渗流模型建立. 岩性油气藏, 2017, 29(6): 108-118. ZHANG L H, SHAN B C, ZHAO Y L, et al. Establishment of apparent permeability model and seepage flow model for shale reservoir. Lithologic Reservoirs, 2017, 29(6): 108-118. DOI:10.3969/j.issn.1673-8926.2017.06.014 |
| [9] |
黄荣樽. 水力压裂裂缝的起裂和扩展. 石油勘探与开发, 1982(5): 65-77. HUANG R Z. Initiation and propagation of fractures in hydraulic fracturing. Petroleum Exploration & Development, 1982(5): 65-77. |
| [10] |
孙文峰, 李玮, 董智煜, 等. 页岩孔隙结构表征方法新探索. 岩性油气藏, 2017, 29(2): 125-130. SUN W F, LI W, DONG Z Y, et al. A new approach to the characterization of shale pore structure. Lithologic Reservoirs, 2017, 29(2): 125-130. DOI:10.3969/j.issn.1673-8926.2017.02.015 |
| [11] |
EATON B A. Fracture gradient prediction and its application in oilfield operations. Journal of Petroleum Technology, 1969, 21(10): 1353-1360. DOI:10.2118/2163-PA |
| [12] |
ANDERSON R A, INGRAM D S, ZANIER A M. Determining fracture pressure gradient from well logs. Journal of Petroleum Technology, 1973, 25(11): 1259-1268. DOI:10.2118/4135-PA |
| [13] |
DASGUPTA S, CHATTERJEE R, MOHANTY S P. Prediction of pore pressure and fracture pressure in Cauvery and KrishnaGodavari basins, India. Marine & Petroleum Geology, 2016, 78: 493-506. |
| [14] |
MA T, ZHANG Q B, CHEN P, et al. Fracture pressure model for inclined wells in layered formations with anisotropic rock strengths. Journal of Petroleum Science & Engineering, 2016, 149: 393-408. |
| [15] |
MA T, WU B, FU J, et al. Fracture pressure prediction for layered formations with anisotropic rock strengths. Journal of Natural Gas Science & Engineering, 2017, 38: 485-503. |
| [16] |
黄荣樽. 地层破裂压力预测模式的探讨. 华东石油学院学报, 1984(4): 16-28. HUANG R Z. A model for predicting formation fracture pressure. Journal of the University of Petroleum, China, 1984(4): 16-28. |
| [17] |
严向阳, 胡永全, 李楠, 等. 泥页岩地层破裂压力计算模型研究. 岩性油气藏, 2015, 27(2): 109-113. YAN X Y, HU Y Q, LI N, et al. Calculation model of breakdown pressure in shale formation. Lithologic Reservoirs, 2015, 27(2): 109-113. DOI:10.3969/j.issn.1673-8926.2015.02.017 |
| [18] |
邓金根, 刘杨, 蔚宝华, 等. 高温高压地层破裂压力预测方法. 石油钻探技术, 2009, 37(5): 43-46. DENG J G, LIU Y, WEI B H, et al. Formation fracture pressure prediction method in high temperature and high-pressure formations. Petroleum Drilling Techniques, 2009, 37(5): 43-46. DOI:10.3969/j.issn.1001-0890.2009.05.010 |
| [19] |
东振, 刘亚东, 鲍清英, 等. 基于断裂力学的煤层气井破裂压力计算方法. 东北石油大学学报, 2015, 39(6): 111-120. DONG Z, LIU Y D, BAO Q Y, et al. Calculation method for fracture pressure of coalbed methane well based on fracture mechanics. Journal of Northeast Petroleum University, 2015, 39(6): 111-120. DOI:10.3969/j.issn.2095-4107.2015.06.013 |
| [20] |
李传亮. 射孔完井条件下的岩石破裂压力计算公式. 石油钻采工艺, 2002, 24(2): 37-38. LI C L. Calculation formula of rock fracture pressure under perforated completion condition. Oil Drilling & Production Technology, 2002, 24(2): 37-38. DOI:10.3969/j.issn.1000-7393.2002.02.024 |
| [21] |
李培超. 射孔完井条件下地层破裂压力修正公式. 上海工程技术大学学报, 2009, 23(2): 157-160. LI P C. Modified formula of formation breakdown pressure for perforation completions of vertical wells. Journal of Shanghai University of Engineering Science, 2009, 23(2): 157-160. DOI:10.3969/j.issn.1009-444X.2009.02.013 |
| [22] |
金衍, 陈勉. 井壁稳定力学. 北京:科学出版社, 2012, 56-58. JIN Y, CHEN M. Wellbore stability mechanics. Beijing:Science Press, 2012, 56-58. |
| [23] |
CHENEVERT M E, PERNOT V. Control of shale swelling pressures using inhibitive water-base muds. SPE 49263, 1998.
|
| [24] |
王京印. 泥页岩井壁稳定性力学化学耦合模型研究. 青岛: 中国石油大学(华东), 2007. WANG J Y. Chemical-mechanical modeling of borehole stability in shale. Qingdao: China University of Petroleum, 2007. |
| [25] |
CHEN G Z, CHENEVERT M E, SHARMA M M, et al. A study of wellbore stability in shales including poroelastic, chemical, and thermal effects. Journal of Petroleum Science and Engineering, 2003, 38: 167-176. DOI:10.1016/S0920-4105(03)00030-5 |
| [26] |
GUO J C, ZHAO Z H, HE S G. A new method for shale brittleness evaluation. Environment Earth Science, 2015, 73: 5800-5865. |
 2019, Vol. 31
2019, Vol. 31



