2. 中国石化西北油田分公司采油一厂, 新疆 轮台 841600
2. No.1 Oil Production Plant, Northwest Oilfield Company, Sinopec, Luntai 841600, Xinjiang, China
在边水气藏的开发过程中,由于边水舌进,将导致气藏水侵、气井见水,从而降低气藏采收率[1]。边水气藏生产井的见水时间预测是气井开发技术调整的基础工作,对其进行合理预测,有利于气藏的高效开发。对于边水突破,国内外已有学者进行了相关研究,史乃光等[2]用系统辨识的方法对见水时间进行预测。石广志等[3]采用数值模拟的方法对边水推进规律进行了研究。Kuo等[4]、王会强等[5-6]基于多孔介质中流体质点的渗流规律对边水气藏和底水气藏气井见水时间进行了计算。吴克柳等[7]对考虑反凝析现象的边水气藏见水时间进行预测,为控制见水时间提供了理论依据。杨芙蓉等[8]推导了考虑非达西效应的高产气井见水时间计算公式。刘广为等[9]推导了适用于水平井的见水时间计算公式。卞亚军等[10]对含底水的水平井的见水时间进行调研,认为数值模拟的方法较好。汪周华等[11]建立了考虑重力及气体非达西效应影响的边水气藏边水突破时间预测模型。李传亮等[12]对含水上升规律进行了研究。黄全华等[13]对带隔板的气藏见水时间进行预测并推导公式。廖恒杰等[14]基于东海西湖凹陷,对水驱气藏气井的产水规律进行了分析,研究了气井的产气特征及水气比上升规律,形成了水驱气藏早期水侵综合识别方法。Guo等[15]建立了考虑硫沉积的高硫气藏气井见水突破时间预测模型。明瑞卿等[16-17]针对凝析气藏开采过程中的底水锥进现象和考虑水平段长度和储层倾角对气藏见水时间进行分析并提出新方法。
以上对于边水气藏水平井见水时间的模型大都是将气体渗流考虑成达西流动,但由于水平井的产量通常比较高,地层中流体渗流速度很大,且越靠近井轴,流速越高,造成的非达西流动效应对见水时间的影响不可忽略。因此,基于多孔介质渗流规律,综合考虑气体非达西效应、气水流度比、原始束缚水饱和度、残余气饱和度、气井距边水的距离、水平段长度等因素,推导适用于边水气藏高产水平井见水时间预测公式,并进行实例计算,以期指导边水气藏科学、高效地开发。
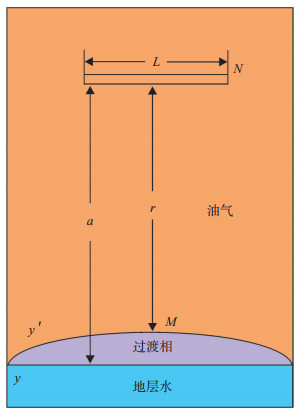
1 物理模型的建立及公式推导有一边水气藏如图 1所示,将其初始气水边界近似看作一条直线,记为y。在离y距离为a处有一口水平生产井,水平井水平段长度为L。根据相关渗流力学理论,采用椭球型[18]作为水平井渗流模型。据现有的边水油气藏水平井水淹规律研究成果,水平井生产水侵以水舌方式推进,因此当气井开始生产后,气水界面开始向井底推进,且气水界面变成曲面y'。
|
下载eps/tif图 图 1 水平井生产边水推进示意图 Fig. 1 Diagram showing edge water propelling in horizontal wells |
基于以上渗流规律,假设M为水舌突进点,N点为水平射孔段的中心位置,M与N之间的距离为r。在满足气水两相基本渗流规律的基础上,对推导过程作以下假设:①储层等厚均质,水相驱替气相的方式为活塞式驱替。②不考虑毛管压力和重力作用。③渗流过程中气水黏度及密度均为定值。④水相渗流符合达西定律,为线性渗流,气相渗流不符合达西定律,为非线性渗流。
根据气水两相渗流规律,考虑气体非达西流动效应,则气水两相运动方程[19]分别为
| $ \frac{{{\rm{d}}{p_{\rm{g}}}}}{{{\rm{d}}r}} = \frac{{{u_{\rm{g}}}{v_{\rm{g}}}}}{{{K_g}}} + \beta {\rho _{\rm{g}}}{v_{\rm{g}}}^2 $ | (1) |
| $ \frac{{{\rm{d}}{p_{\rm{w}}}}}{{{\rm{d}}r}} = \frac{{{\mu _{\rm{w}}}{v_{\rm{w}}}}}{{{k_{\rm{w}}}}} $ | (2) |
式中:pg为气相压力,MPa;pw为水相压力,MPa;r为水质点向井移动的距离,m;μg为气相黏度,mPa·s;μw为水相黏度,mPa·s;υg为气相渗流速度,m/d;υw为水相渗流速度,m/d;Kg为气相渗透率,mD;Kw为水相渗透率,mD;β为描述孔隙介质紊流影响的系数[20-22],m-1;ρg为气相密度,g/cm3。
不考虑毛管压力作用,在气水界面上,气相和水相的压力梯度相等。则有
| $ \frac{{{\rm{d}}{p_{\rm{g}}}}}{{{\rm{d}}r}}\left| {_{y'}} \right. = \frac{{{\rm{d}}{p_{\rm{w}}}}}{{{\rm{d}}r}}\left| {_{y'}} \right. $ | (3) |
将式(1)—(2)代入式(3),并按照矿场实用制单位将公式中的单位进行统一,可得水相的渗流速度为
| $ {v_{\rm{w}}} = \frac{{{v_{\rm{g}}}}}{{{M_{{\rm{gw}}}}}} + 1.157 \times {10^{ - 16}}\beta {\rho _{\rm{g}}}{v_{\rm{g}}^2}\frac{{{K_{\rm{w}}}}}{{{u_{\rm{w}}}}} $ | (4) |
式中:Mgw为气水流度比,Mgw=
在多孔介质中,考虑孔隙度、原始束缚水饱和度及残余气饱和度的影响,水质点在dt时间内向水平射孔段的中心位置N点移动的距离为
| $ {\rm{d}}r = \frac{{{v_{\rm{w}}}{\rm{d}}t}}{{\varphi \left( {1 - {S_{{\rm{wi}}}} - {S_{{\rm{gr}}}}} \right)}} $ | (5) |
对式(5)进行变形并积分,可得水质点从初始气水界面运动到井底的突破时间
| $ {t_{{\rm{bt}}}} = \varphi \left( {1 - {S_{{\rm{wi}}}} - {S_{{\rm{gr}}}}} \right)\int_0^a {\frac{1}{{{M_{{\rm{gw}}}}{v_{\rm{g}}} + 1.157 \times {{10}^{ - 16}}\beta {\rho _{\rm{g}}}\frac{{{K_{\rm{w}}}}}{{{\mu _{\rm{w}}}}}{v_{\rm{g}}}^2}}{\rm{d}}r} $ | (6) |
式中:φ为孔隙度;Swi为束缚水饱和度;Sgr为残余气饱和度。
假设水平井的泄气区为椭圆形。水驱前缘上M点处所在的等势面也是椭圆形,则其长半轴长度为
| $ {v_{\rm{g}}} = \frac{{{q_{\rm{g}}}{B_{\rm{g}}}}}{{\left( {2{\rm{ \mathsf{ π} }}r + 2L} \right)h}} $ | (7) |
式中:qg为气井产量,m3/d;Bg为天然气体积系数;h为储集层厚度,m;L为水平井水平段长度,m。
将式(7)代入式(6)可得
| $ {t_{{\rm{bt}}}} = \varphi \left( {1 - {S_{{\rm{wi}}}} - {S_{{\rm{gr}}}}} \right)\int_0^a {\frac{1}{{\frac{A}{{2{\rm{ \mathsf{ π} }}r + 2L}} + \frac{B}{{{{\left( {2{\rm{ \mathsf{ π} }}r + 2L} \right)}^2}}}}}{\rm{d}}r} $ | (8) |
其中A=
对式(8)进行2次换元积分可求解得
| $ \begin{array}{l} {t_{bt}} = \varphi \left( {1 - {S_{{\rm{wi}}}} - {S_{{\rm{gr}}}}} \right)\left[ {\frac{{{\rm{ \mathsf{ π} }}{a^2} + 2aL}}{A} + } \right.\\ \;\;\;\;\;\;\left. {\frac{{{B^2}}}{{2{\rm{ \mathsf{ π} }}{A^3}}}\ln \left( {1 + \frac{{2{\rm{ \mathsf{ π} }}Aa}}{{2AL + B}}} \right) - \frac{{Ba}}{{{A^2}}}} \right] \end{array} $ | (9) |
式(9)即为考虑气体非达西效应的均质各向同性边水气藏水平井见水时间计算公式。
同理推导不考虑气体非达西效应的均质各向同性边水气藏水平井见水时间计算公式[7]为:
| $ {t_{{\rm{bt}}}} = \frac{{\varphi h\left( {1 - {S_{{\rm{wi}}}} - {S_{{\rm{gr}}}}} \right)\left( {\frac{{{K_{{\rm{gwi}}}}}}{{{\mu _{\rm{g}}}}}} \right)}}{{{q_{\rm{g}}}{B_{\rm{g}}}\left( {\frac{{{K_{{\rm{wgr}}}}}}{{{\mu _{\rm{w}}}}}} \right)}}\left( {{\rm{ \mathsf{ π} }}{a^2} + 2aL} \right) $ | (10) |
式中:Kgwi为束缚水饱和度Swi下的气相渗透率,mD;Kwgr为残余气饱和度Sgr下的水相渗透率,mD。
2 实例计算及影响因素分析实例一,某边水气藏中有一口生产水平井,储层厚度h=10 m,孔隙度φ=0.052,束缚水饱和度Swi= 0.43,残余气饱和度Sgr=0.11,束缚水饱和下的气相渗透率Kgwi=0.217 mD,残余气饱和下的水相渗透率Kwgr=0.364 mD,气相渗透率Kg=9.81 mD,气相密度ρg=0.282 9 g/cm3,天然气体积系数Bg=0.003 13 m3/m3,气相黏度μg=0.034 8 mPa·s,水相黏度μw=0.39 mPa·s。水平井水平段长度L=480 m,水平段中心位置距初始气水边界距离a=450 m,见水前平均产量qg=56万m3/d。
将上述基础参数代入式(9)可求得考虑非达西效应的水平井见水时间为935 d,代入式(10)求得考虑达西效应的水平井见水时间为973 d。
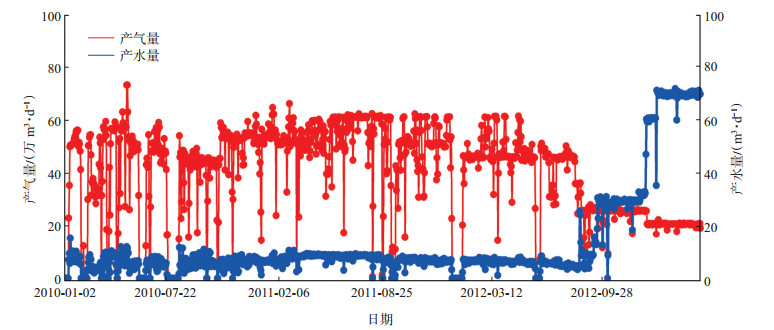
这口水平井的日产气、日产水曲线如图 2所示。从图 2可以看出,此井于2010年1月8日投产,2012年6月10日开始见水,然后产量迅速下降,其见水时间为884 d。
|
下载eps/tif图 图 2 水平井1的产气量、产水量曲线 Fig. 2 Gas and water productivity curves of horizontal well 1 |
将水平井实际见水时间与本文公式计算的见水时间进行对比可知,其相对误差为5.8%,与考虑非达西效应的计算结果相比,其相对误差较大,为10.07%。这是因为受气体非达西效应的影响,导致气体流速增大,因此边水突破时间变短,也说明了本文的计算公式更符合实际情况。
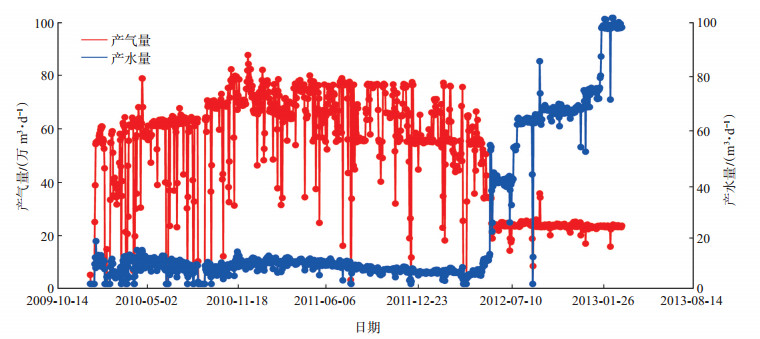
实例二,取实例一相同地层内另外一口边水气藏水平井实际生产情况进行分析(图 3)。该井见水前平均产量qg=53万m3/d,其他参数与实例一一致。根据井场资料,该井于2010年1月8日投产,2012年6月12日见水,其后产量迅速下降,见水时间为896 d。选用不考虑达西效应的公式计算可得其见水时间为1 028 d,其相对误差为14.73%。选本文公式计算可得该水平井的见水时间为992 d,其相对误差为10.7%。
|
下载eps/tif图 图 3 水平井2的产气量、产水量曲线 Fig. 3 Gas and water productivity curves of horizontal well 2 |
非达西效应、气井距初始气水边界距离、水平井水平段长度和气井产量均是影响边水气藏见水时间的几个重要因素,本文取实例一进行影响因素分析。
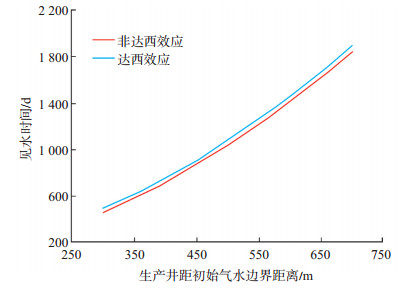
图 4是在该边水气藏在其他参数不变的情况下,模拟改变生产井与初始气水边界距离,分别为考虑非达西效应和考虑达西效应来进行的,可见见水时间与不同的生产井距初始气水边界距离关系较大。从图 4可以看出,水平井距初始气水边界距离越大,其见水时间越长。在与初始气水边界距离一定的情况下,考虑了非达西效应的见水时间比考虑达西效应的见水时间更短。
|
下载eps/tif图 图 4 见水时间与水平井距气水边界距离关系曲线 Fig. 4 Relationship between water breakthrough time and distance from horizontal well to initial gas-water interface |
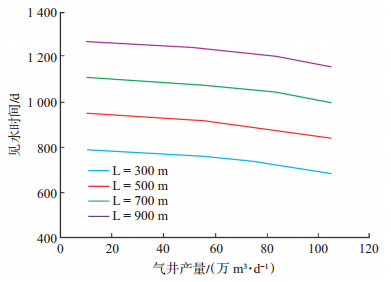
图 5是在该气藏其他参数不改变的情况下,通过改变一系列不同水平段长度时的见水时间随气井产量变化的关系曲线。从图 5可以看出,随着水平井水平段长度的增加,边水突破时间变长。这是由于随着水平段长度的增加,水平井渗流面积变大,渗流速度减小,因此有利于抑制边水舌进。在水平段长度一定的情况下,见水时间随着气井产量的增大而减小,且减小的速度变快,这是因为随着气井产量的增大,渗流速度增大,且当气井产量增大到一定程度以后,气体高速渗流造成的非达西效应不可忽略,将会加速气井见水。
|
下载eps/tif图 图 5 见水时间与气井产量关系曲线 Fig. 5 Relationship between water breakthrough time and production of gas well |
(1)基于多孔介质流体渗流规律,建立了考虑非达西效应的渗流模型,推导出边水气藏水平井见水时间预测公式。通过2口井实例计算表明,与仅考虑达西效应的高产井计算公式相比,考虑非达西效应的高产水平井见水时间预测公式的计算结果介于实际见水时间和与仅考虑达西效应见水时间之间,计算精度更高,更符合边水气藏水平井见水的实际情况。
(2)进一步讨论了水平井与初始气水边界的距离、水平井水平段长度和气井产量对见水时间的影响。分析后得出,边水气藏水平井见水时间随着水平井距初始气水边界距离的增加而增加;随着水平段长度的增加而增加;随着气井产量的增大而减小,且减小的速度逐渐变快。
致谢: 西南石油大学孙雷给予了悉心指导,在此表示感谢!
| [1] |
张烈辉, 梅青艳, 李允, 等. 提高边水气藏采收率的方法研究. 天然气工业, 2006, 26(11): 101-103. ZHANG L H, MEI Q Y, LI Y, et al. The method of improving recovery efficiency of edge water drive gas reservoirs. Natural Gas Industry, 2006, 26(11): 101-103. DOI:10.3321/j.issn:1000-0976.2006.11.031 |
| [2] |
史乃光, 杨维宁, 杨正文. 用系统辨识方法预测气井见水时间. 天然气工业, 1992, 12(1): 25-31. SHI N G, YANG W N, YANG Z W. Using system identification method to predict water breakthrough time in gas well. Natural Gas Industry, 1992, 12(1): 25-31. |
| [3] |
石广志, 冯国庆, 张烈辉. 某边水油藏开发数值模拟研究. 天然气勘探与开发, 2006, 29(2): 21-24. SHI G Z, FENG G Q, ZHANG L H. Numerical simulation in an edge-water oil reservoir. Natural Gas Exploration & Development, 2006, 29(2): 21-24. DOI:10.3969/j.issn.1673-3177.2006.02.006 |
| [4] |
KUO M C T, DESBRISAY C L. A simplified method for water coning predictions. SPE 12067, 1983. https://www.onepetro.org/conference-paper/SPE-12067-MS
|
| [5] |
王会强, 李晓平, 吴锋, 等. 边水气藏气井见水时间预测方法. 特种油气藏, 2008, 15(4): 73-74. WANG H Q, LI X P, WU F, et al. Prediction of water breakthrough time in gas reservoirs with edge water. Special Oil and Gas Reservoirs, 2008, 15(4): 73-74. DOI:10.3969/j.issn.1006-6535.2008.04.017 |
| [6] |
王会强, 李晓平, 杨琪, 等. 底水气藏见水时间预测方法. 新疆石油地质, 2007, 28(1): 92-93. WANG H Q, LI X P, YANG Q, et al. A Prediction of water breakthrough time in gas reservoirs with bottom water. Xinjiang Petroleum Geology, 2007, 28(1): 92-93. DOI:10.3969/j.issn.1001-3873.2007.01.025 |
| [7] |
吴克柳, 李相方, 张公涛, 等. 考虑反凝析的边水凝析气藏见水时间预测新方法. 科学技术与工程, 2011, 11(19): 4574-4577. WU K L, LI X F, ZHANG G T, et al. A novel approach to predict water breakthrough time in gas condensate reservoir with edge water considering retrograde condensation. Science Technology and Engineering, 2011, 11(19): 4574-4577. DOI:10.3969/j.issn.1671-1815.2011.19.040 |
| [8] |
杨芙蓉, 樊平天, 贺静, 等. 边水气藏高产气井见水时间预测方法. 科学技术与工程, 2013, 13(29): 8745-8747. YANG F R, FAN P T, HE J, et al. An approach to predict water breakthrough time in high gas rate wells of gas reservoirs with edge water. Science Technology and Engineering, 2013, 13(29): 8745-8747. DOI:10.3969/j.issn.1671-1815.2013.29.036 |
| [9] |
刘广为, 姜汉桥, 李龙元, 等. 边水油藏水平井见水时间预测新方法. 科学技术与工程, 2014, 14(2): 84-86. LIU G W, JIANG H Q, LI L Y, et al. New method of estimating water breakthrough time for horizontal wells in edge water drive reservoir. Science Technology and Engineering, 2014, 14(2): 84-86. DOI:10.3969/j.issn.1671-1815.2014.02.019 |
| [10] |
卞亚军, 李立峰. 底水油藏水平井见水时间预测方法研究概述. 内江科技, 2015(3): 47. BIAN Y J, LI L F. An overview of the prediction method of water breakthrough time in horizontal wells of bottom water reservoir. Neijiang Technology, 2015(3): 47. DOI:10.3969/j.issn.1006-1436.2015.03.035 |
| [11] |
汪周华, 王子敦, 邓丹, 等. 考虑重力及气体非达西效应影响的边水气藏边水突破时间预测模型. 石油钻采工艺, 2016, 38(2): 210-215. WANG Z H, WANG Z D, DENG D, et al. Model for prediction of edge-water breakthrough time in reservoirs with edge water with consideration to effects of gravity and non-Darcy effect of gases. Oil Drilling & Production Technology, 2016, 38(2): 210-215. |
| [12] |
李传亮, 朱苏阳. 关于油藏含水上升规律的若干问题. 岩性油气藏, 2016, 28(3): 1-5. LI C L, ZHU S Y. Some topics about water cut rising rule in reservoirs. Lithologic Reservoirs, 2016, 28(3): 1-5. DOI:10.3969/j.issn.1673-8926.2016.03.001 |
| [13] |
黄全华, 陆云, 陈冲. 带隔板底水气藏见水时间预测方法. 岩性油气藏, 2016, 28(4): 82-87. HUANG Q H, LU Y, CHEN C. Prediction of water break through time for bottom-water gas reservoir with barrier. Lithologic Reservoirs, 2016, 28(4): 82-87. DOI:10.3969/j.issn.1673-8926.2016.04.011 |
| [14] |
廖恒杰, 杨志兴, 李元生, 等. 西湖凹陷气藏出水规律及控制因素. 岩性油气藏, 2017, 29(6): 135-141. LIAO H J, YANG Z X, LI Y S, et al. Water production laws and controlling factors of gas reservoir in Xihu Sag. Lithologic Reservoirs, 2017, 29(6): 135-141. DOI:10.3969/j.issn.1673-8926.2017.06.017 |
| [15] |
GUO X, WANG P, LIU J, et al. Gas-well water breakthrough time prediction model for high-sulfur gas reservoirs considering sulfur deposition. Journal of Petroleum Science and Engineering, 2017, 157: 999-1006. DOI:10.1016/j.petrol.2017.08.020 |
| [16] |
明瑞卿, 贺会群, 胡强法. 底水凝析气藏见水时间预测新方法. 特种油气藏, 2018, 25(5): 99-103. MING R Q, HE H Q, HU Q F. A new method to predict water breakthrough time in condense gas reservoir with bottom-aquifer. Special Oil and Gas Reservoirs, 2018, 25(5): 99-103. DOI:10.3969/j.issn.1006-6535.2018.05.019 |
| [17] |
明瑞卿, 贺会群, 胡强法, 等. 边水凝析气藏高产井见水时间预测新模型. 特种油气藏, 2018, 25(2): 76-79. MING R Q, HE H Q, HU Q F, et al. A new model to predict the water breakthrough time of high-rate well in condensate gas reservoir with edge-aquifer. Special Oil and Gas Reservoirs, 2018, 25(2): 76-79. DOI:10.3969/j.issn.1006-6535.2018.02.014 |
| [18] |
陈元千. 水平井产量公式的推导与对比. 新疆石油地质, 2008, 29(1): 68-71. CHEN Y Q. Derivation and correlation of production rate formula for horizontal well. Xinjiang Petroleum Geology, 2008, 29(1): 68-71. |
| [19] |
黄全华, 陆云, 付云辉, 等. 考虑非达西效应的底水气藏见水时间预测方法. 科学技术与工程, 2016, 16(14): 137-140. HUANG Q H, LU Y, FU Y H, et al. An approach to predict water breakthrough time of gas reservoirs with bottom water in consideration of non-Darcy flow. Science Technology and Engineering, 2016, 16(14): 137-140. DOI:10.3969/j.issn.1671-1815.2016.14.025 |
| [20] |
李士伦. 天然气工程. 北京: 石油工业出版社, 2010: 89-90. LI S L. Natural gas engineering. Beijing: Petroleum Industry Press, 2010: 89-90. |
| [21] |
陈元千, 董宁宇. 确定高速速度系数β的方法及其相关经验公式. 断块油气田, 1998, 5(6): 20-26. CHEN Y Q, DONG N Y. A method of determining high-velocity coefficient β and its correlation. Fault-Block Oil & Gas Field, 1998, 5(6): 20-26. |
| [22] |
李元生, 李相方, 藤赛男, 等. 气藏高速油流系数新的经验公式的确定. 断块油气田, 2011, 18(5): 607-610. LI Y S, LI X F, TENG S N, et al. A new correction equation determining high velocity turbulence coefficient of gas reservoirs. Fault-Block Oil & Gas Field, 2011, 18(5): 607-610. |
 2019, Vol. 31
2019, Vol. 31




