2. 成都理工大学 地球物理学院, 成都 610059
2. College of Geophysics, Chengdu University of Technology, Chengdu 610059, China
随着油气勘探领域向深层、岩性地层油气藏的转变,储层预测更加依赖高精度地震资料处理及解释方法[1]。地下地层介质物性及流体性质变化会引起地震波形的微弱变化,通过识别波形变化特征就有可能圈定出含油气储层[2]。时频分析和地震波形分类是常见的用来检测地震波形变化的处理、解释方法。
时频分析是研究非平稳信号时变特征的一种有效方法,广泛应用于地震资料处理等领域[3]。传统的时频分析方法可分为3类:①线性时频分析,包括短时傅里叶变换(Short-time Fourier Transform,STFT) [3]、小波变换(Continuous Wavelet Transform,CWT) [3-4]、S变换[5-6]、广义S变换[5-7]、匹配追踪[8]等。受Heisenberg测不准原理制约,这类方法难以同时取得较高的时间分辨率和频率分辨率[3]。②双线性时频分析,这类方法虽然具有较高的时频聚焦性,但存在交叉项干扰,使其时频谱难以解释。此类方法主要包括Wigner-Ville分布[9]及其衍生方法。③结合经验模态分解的时频分析方法,具有较高时频分辨率,且不受交叉项干扰,但缺点是计算效率低、受端点效应影响[10-11]等。该类方法包括HilbertHuang变换[12-13]及改进型(变分模态分解[14]和经验小波分解[15]等)。近年来,时频分析方法主要是对时频分布做进一步处理,以获得较高的时频分辨率,主要包括:Auger等[16]提出的时频重排,将时频谱重排到时频脊线上,能够取得较高的时频分辨率,但不支持信号重构;Daubechies等[17]提出的同步压缩变换(Synchrosqueezed Wavelet Transforms,SST),Herrera等[18]将其用于地震信号时频分析,该方法采用挤压算法,支持信号重构,但时频分辨率不足;受SST算法思想的启发,Yu等[19]提出的同步提取变换(Synchroextracting Transform,SET)具有时频分辨率高、较好的噪声鲁棒性、支持信号重构、参数简单等优点,该研究可用于地震信号时频分析计算。
地震波形分类采用无监督神经网络方法对地震波形进行分类运算,并广泛应用于地震相分析、储层预测等解释流程[20],常使用的方法是自组织神经网络(self-organizing map,SOM)。主要的研究成果有:Balch[20]最早将波形分类方法引入地震资料解释;Coleou等[21]总结了波形分类方法的原理和计算流程;Gao[22]将SOM算法引入纹理属性聚类分析;Roy等[23]提出基于SOM地震多属性聚类的地震相分析方法。SOM地震多属性聚类也存在明显的缺点,如缺少代价函数、学习速率选择和调整规则缺少理论支撑、缺少收敛证明和没有定义概率模型等[24-26]。针对这些缺点,Bishop等[27]提出了生成拓扑映射(generative topographic mapping,GTM);Wallet等[28]最早将GTM应用于地震波形分类;Roy等[29]将GTM应用于地震多属性聚类分析;Zhao等[2]通过对不同算法进行对比,认为GTM方法具有明显优势。
单纯时域或频域分析方法难以精确描述含油气储层与非储层物性差异引起地震波形的微弱变化,传统的时域波形分类方法也难以精细刻画储层形态。因此,将时频分析和波形分类2种方法结合起来,提出一种适合SET和GTM的时频域波形分类方法,并将该方法应用于储层预测。
1 方法原理 1.1 同步提取变换原理通过时频谱可以研究信号瞬时振幅、瞬时频率等时变特征,准确提取这些信息是地震信号处理和解释(信号能量衰减分析、噪声压制和属性提取)的前提条件。
STFT是最常用的时频分析算法之一。利用傅里叶变换,可以实现最快的计算效率。由于STFT采用有限长窗函数,受Heisenberg测不准原理的影响,时频能量不能聚焦。当窗函数g ∈ L2(R)时,对信号s ∈ L2(R)的STFT定义增加相移eiωt如下:
| $ {G_{\text{e}}}\left( {t, \omega } \right) = \int_{-\infty }^{ + \infty } {g\left( {u-t} \right) \cdot s\left( u \right) \cdot {{\text{e}}^{-{\text{i}}\omega \left( {u - t} \right)}}{\text{d}}u} $ | (1) |
式中:Ge(t, ω)为增加相移后的频谱函数;t为时间,s;ω为角频率,rad/s;g(u - t)为时移t单位的窗函数;u为时间积分变量;s(u)为待分析信号。
式(1)中积分核相当于待分析信号与窗函数的卷积,说明时域加窗,会降低频率分辨率。因此,国内外学者提出许多提高STFT时频分辨率的方法[16-19],SET是其中时频分辨率高、噪声鲁棒性好的一种。SET的思想是通过对STFT时频谱进行重排处理,使时频谱能量聚焦在瞬时频率脊线上,从而获得接近于理想的时频谱分布。
根据Parseval定理,式(1)可改写为
| $ {G_{\text{e}}}\left( {t, \omega } \right) = \frac{1}{{2\pi }}\int_{-\infty }^{ + \infty } {\hat g\left( {\omega-\xi } \right) \cdot \hat s\left( \xi \right) \cdot {{\text{e}}^{-{\text{i}}\xi t}}{\text{d}}\xi } $ | (2) |
式中:
为了便于分析,令s(t)为的单分量谐波信号
| $ {s_h}\left( t \right) = A \cdot {{\text{e}}^{-{\text{i}}{\omega _0}t}} $ | (3) |
式中:A为谐波信号幅值;ω0为信号角频率,rad/s。
其Fourier变换为
| $ \hat s\left( \xi \right) = 2\pi A \cdot \delta \left( {\xi-{\omega _0}} \right) $ | (4) |
式中:δ(·)为单位冲击函数。
将式(4)代入式(2)可得
| $ {G_{\text{e}}}\left( {t, \omega } \right) = A \cdot \hat g\left( {\omega-{\omega _0}} \right) \cdot {{\text{e}}^{-{\text{i}}{\omega _0}t}} $ | (5) |
由式(5)可以看出:在理想时频分布中,信号能量仅分布在ω = ω0的点上,而STFT相当于一个卷积过程,卷积后信号能量分布在[ω-ω0, ω + ω0]的支撑上。当ω = ω0时取得最大幅值
对式(5)等号两端求时间t的偏导数,可得
| $ \frac{{\partial {G_{\text{e}}}\left( {t, \omega } \right)}}{{\partial t}} = {G_{\text{e}}}\left( {t, \omega } \right) \cdot {\text{i}} \cdot {\omega _0} $ | (6) |
式(6)中,等号左边为时频平面中某点的频率。说明在频谱支撑范围[ω-ω0, ω + ω0]内,时频谱系数具有相同的瞬时频率ω0。SET算法的思路是利用瞬时频率脊线上时频分布系数最大、噪声鲁棒性最好的特性,仅保留频率脊线上的时频分布系数,其他时频分布系数做零值化处理。处理后时频分布为
| $ T{\text{e}}\left( {t, \omega } \right) = {G_{\text{e}}}\left( {t, \omega } \right) \cdot \delta \left( {\omega-{\omega _0}} \right) $ | (7) |
式中:Te(t, ω)为信号同步提取变换。
文献[19]将δ(ω - ω0)称之为同步提取算子(synchroextracting operator,SEO)。
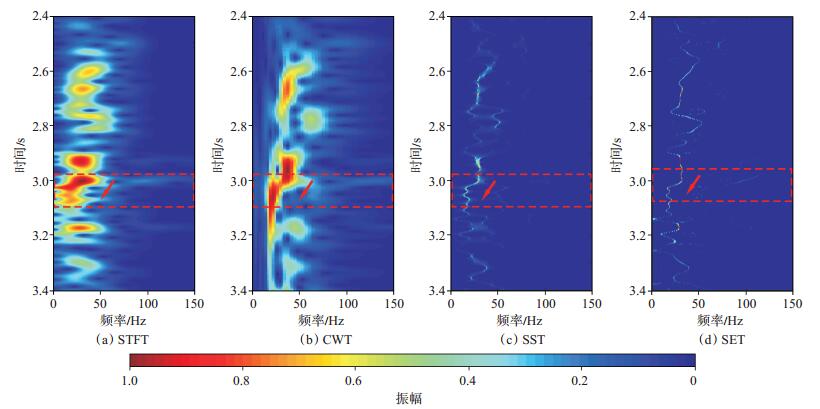
图 5以实际井旁地震道为例,验证了SET具有优于STFT,CWT和SST的时频分辨率,能够精细刻画非平稳信号瞬时频率变化特征。
|
下载eps/tif图 图 5 井1旁道时频分析对比(振幅归一化) Fig. 5 Comparison of time-frequency decomposition results of well 1 (amplitude normalization) |
GTM属于非线性隐变量模型,通过非线性映射函数y(x,W)(W为参数矩阵)将L维隐变量空间(x ∈ RL)映射为一个L维非欧流形ζ嵌入在D维数据空间(t ∈ RD)中。一般L < D,用少量的隐变量表示高维数据变量。图 1以隐变量维度L = 2和数据空间维度D = 3为例说明GTM的映射思路。隐变量空间维度有2个变量x1和x2,数据空间维度具有3个变量t1,t2和t3,ζ为映射函数形成的流形嵌入在数据空间维度中。

|
下载eps/tif图 图 1 GTM模型映射思路[21] Fig. 1 Nonlinear mapping of the latent space to the data space in GTM |
Bishop等[27]详述了GTM的原理和算法,这里仅介绍其基本原理。设隐变量空间维度的先验概率密度函数为p(x),映射到数据空间维度的条件概率密度函数用高斯噪声模型建模如下:
| $ p\left( {t|x, W, \beta } \right) = {\left( {\frac{\beta }{{2\pi }}} \right)^{-\frac{D}{2}}}\exp \left\{ {-\frac{\beta }{2}{{\left\| {t-y\left( {x, W} \right)} \right\|}^2}} \right\} $ | (8) |
式中:p(t|x, W, β)为条件概率密度函数;y(x, W)为映射函数;W为参数矩阵;β为高斯分布方差的倒数;D为数据空间维度;x和t分别为隐变量和训练数据。
由式(8)和Bayes公式[27],得到数据空间维度的后验概率密度函数
| $ p\left( {t|W, \beta } \right) = \int {p\left( {t|x, W, \beta } \right)p\left( x \right){\text{d}}x} $ | (9) |
式中:p(t|W, β)为后验概率密度函数。
设训练数据集D = (t1,…,tN),GTM网络训练目标是寻求最优的W和β使似然函数最大。最优化过程采用EM算法(Expectation Maximization Algorithm),详见文献[27]。
| $ L\left( {W, \beta } \right) = \ln \prod\limits_{n = 1}^N {p\left( {{t_n}|W, \beta } \right)} $ | (10) |
式中:L(W, β)为似然函数;N为训练样本数,个。
训练完成后,得到最佳的W*和β*使流形ζ能够得到最佳拟合训练集D,通过Bayes公式[27]就能够实现数据空间维度到隐变量空间维度的逆映射,达到数据降维的目的。
| $ p\left( {x|t, {W^*}, {\beta ^*}} \right) = \frac{{p\left( {t|{W^*}, {\beta ^*}} \right) \times p\left( x \right)}}{{p\left( {t|{W^*}, {\beta ^*}} \right)}} $ | (11) |
式中:p(x|t, W*, β*)为条件概率密度函数;W*为最优参数矩阵;β*为一组最优的高斯分布方差的倒数。
在地球物理学应用领域,为了便于分类结果图形化显示,一般取隐变量空间维度L = 2,参数W和β初始化并将训练数据集D做主成分(Principalcomponent analysis,PCA)进行分析确定。
为了验证GTM波形分类算法的有效性,以IRIS数据集为例进行试算。该数据集是机器学习领域常用来对比无监督神经网络算法优劣的标准数据集之一。该数据具有4个维度的特征量,因此,须要对数据进行分类运算,才能实现数据可视化。优秀的分类算法能够将数据集内相似的元素聚为一类,同一类元素具有较好的类内相似性,而类间数据具有较好的离散性。图 2为GTM和SOM的2种算法分类对比图,图中以3种不同颜色分别表示出了不同的类别标号。图 2 (a)为GTM网络分类,采用二维隐变量层,相当于将原数据集由四维变量映射为二维变量,从图中可以看出,同类数据具有较好的聚集性,类间具有良好的分离性。图 2 (b)为SOM网络分类,采用二维竞争层,但类内数据的聚集性及类间数据的分离性均较GTM算法差。上述2种程序算法的运行时间分别为1.170 0 s和2.745 6 s,可以看出在GTM算法取得较好计算效果的同时,具有较高的计算效率。

|
下载eps/tif图 图 2 IRIS数据分类对比(归一化) Fig. 2 Comparison of classification results of IRIS (normalized) |
Fourier变换能够将满足Dirichlet条件的信号分解为一系列单频指数信号或余弦信号的线性组合,实现时域和频域的映射。受之启发,借助SET时频分析方法将复杂的地震波形分解为一系列简单波形(不同频率、不同时移量)的线性组合,将分解后的简单波形集称之为时频域波形(或时频域波形集),时频域的内涵体现在分解出的每一个波形具有不同的频率和时移量。在时频域储层预测中,常用的谱分解和低频阴影本质上也是检测这种时频域波形变化的,而这类方法在实际应用中常面临着单频选择困难的问题。
地震信号的SET分解可以看作是波形特征的提取过程,SET分解后地震波形的微弱变化在时频谱上能够产生明显的异常,同时SET分解后数据量增大,信息冗余也导致解释困难。因此,对SET分解后的时频域波形采用GTM算法进行波形分类,对分类结果用测井数据标定,就能提高解释效率。时频域波形分类方法流程图如图 3所示。

|
下载eps/tif图 图 3 时频域波形分类方法计算流程 Fig. 3 Calculation process of waveform classification in time-frequency domain |
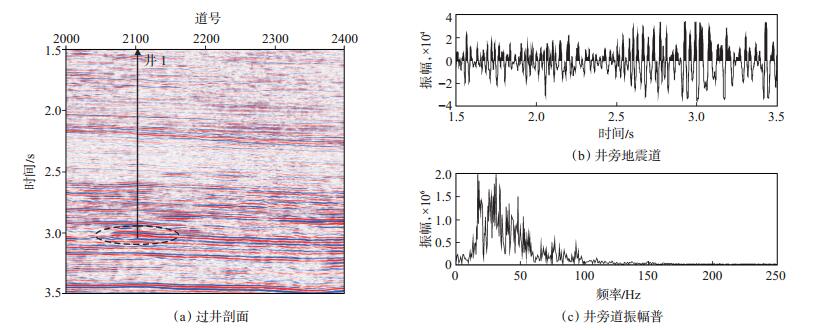
为了验证基于时频域波形分类储层预测方法的有效性,以新疆塔里木盆地北部某油田的地震数据为例进行试算。研究对象为该区三叠系中油组储层,储层沉积相为辫状河河道砂体。研究区共有3口井钻遇中油组目的层,测井和钻井资料均揭示目的层段的井1为含油层,井2为含水层段,井3为油水同层。图 4 (a)为该区过井1 (图中竖线)的地震剖面,目的层深度为2 970~3 050 ms(图中虚框),图 4(b)为井旁地震道,图 4(c)为该道信号振幅谱。从图 4可以看出,单独依靠时域信号或频谱信息难以实现储层预测。因此,精确反映储层地震信号瞬时信息变化必须借助时频分析方法。
|
下载eps/tif图 图 4 过井剖面和井旁道分析 Fig. 4 Analysis of cross section through well 1 and seismic trace near the borehole |
地层介质具有黏滞性,对地震波产生吸收衰减,频率越高衰减越快,与地层水相比,油气具有更低的Q(品质因子)值,当储层富集油气时,会对地震波高频分量产生较大衰减。Liu[30]通过岩石物理实验,揭示了油气对储层底界面反射系数的影响大于顶面,它不仅影响反射波的振幅,还影响其到达的时间,而低频、高频成分到达时间的差异又是造成低频阴影的主要原因[图 5(a)]。通过时频分析就有可能检测这种频谱的变化,以达到实现流体性质预测的目的。合理选择时频分析算法是其成功应用的关键,合适的时频分析方法既要有良好的时频分辨率,还要能够精细刻画信号局部层次结构[5]。井1旁道时频分析对比如图 5所示,其中图 5 (a) ~(d)分别为井旁道的STFT,CWT,SST和SET的时频谱,从图中可以看出,储层位置存在明显的低频阴影现象(图中箭头)。对比这4种时频分析方法可以发现,SST和SET本质上属于时频重排方法,能够将时频能量聚焦到脊线上,因而具有较高的分辨率,反映了非平稳信号瞬时频率的变化特征,其中SET具有最高的时频分辨率,从时频谱中可以精确描述地震信号的瞬时信息(瞬时频率、瞬时振幅),STFT时频分辨率最低。因此,以SET作为时频分析方法,克服单纯时域、频域分析的缺陷,提高地震资料解释的精细程度。将其应用于波形分类,可提高分类结果的精确度和可信度。
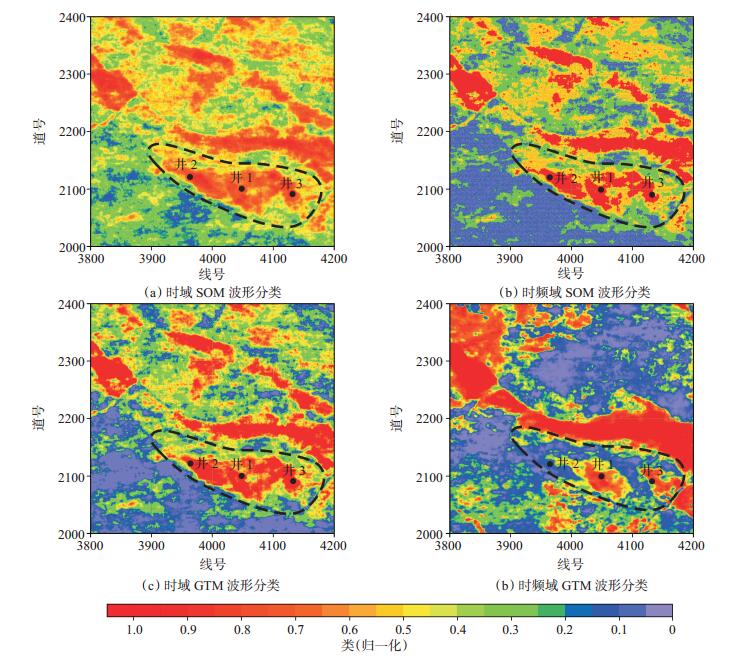
为了便于对比分析,对分类结果做了归一化处理。图 6(a)和图 6(b)均为传统时域波形分类,图 6(c)和图 6(d)均为结合SET的时频域波形分类。图 6(a)为时域SOM波形分类,可看出储层地质体界限模糊,储层内幕刻画不清楚,图中识别出的储层范围大于实际储层范围(图中虚框,图中井2识别为储层);图 6(b)为时域GTM波形分类,与图 6(a)对比,图 6(b)中储层地质体边界刻画清晰,储层内部不均匀性有所刻画(图中虚框);图 6 (c)为时频域SOM波形分类,储层地质体边界和内幕刻画比时域波形分类清晰,但地震资料解释与实际地质信息不够吻合(图中虚框,井2识别为储层);图 6(d)为时频域GTM波形分类,可以看出储层地质体界限清晰,储层内幕不均匀性得到较好刻画(图中虚框),储层解释和实际地质信息吻合(图中含水储层井2位于解释储层外,油水同层,井3位于解释储层范围边缘)。因此,基于时频域GTM波形分类的储层预测方法能够较好地刻画储层地质体边界和内幕,地震资料解释与实际地质信息吻合较好,该方法应用于地震资料解释是有效可行的,能够提高储层预测的准确性。
|
下载eps/tif图 图 6 时频域波形分类方法对比(归一化) Fig. 6 Comparison of waveform classification methods in time-frequency domain (normalization) |
(1) 提出一种结合SET时频分析和GTM波形分类的时频域波形分类方法,该方法利用SET高精度时频分析,能够精细刻画储层含油气引起的微弱地震波形变化。通过GTM网络对地震信号时频谱进行分类,在空间上对储层地质体的边界和内幕进行精细刻画,提高了储层预测的准确性。
(2) 实际工区资料应用表明,该方法解释的储层范围与地质资料吻合,地震资料解释精度和可信度均较高。
(3) GTM网络参数(隐变量层维度、隐变量层节点数量)都对聚类结果和计算效率有一定影响,应用中需针对实际地震数据进行选择。
| [1] |
熊翥. 地层、岩性油气藏地震勘探方法与技术. 石油地球物理勘探, 2012, 47(1): 1-18. XIONG Z. Seismic exploration for strati-lithologic reservoirs. Oil Geophysical Prospecting, 2012, 47(1): 1-18. |
| [2] |
ZHAO T, ROY A, JAYARAM V, et al. A comparison of classification techniques for seismic facies recognition. Interpretation, 2015, 3(4): SAE29-SAE58. DOI:10.1190/INT-2015-0044.1 |
| [3] |
BOASHASH B. Time-frequency signal analysis and processing:a comprehensive reference. London: Academic Press, 2015.
|
| [4] |
张猛刚, 洪忠, 窦玉坛, 等. 时频分析在苏里格地区含气性检测中的应用. 岩性油气藏, 2013, 25(5): 76-80. ZHANG M G, HONG Z, DOU Y T, et al. Application of timefrequency analysis technology to the gas detection in Sulige area. Lithologic Reservoirs, 2013, 25(5): 76-80. |
| [5] |
陈学华, 贺振华, 黄德济, 等. 时频域油气储层低频阴影检测. 地球物理学报, 2009, 52(1): 215-221. CHEN X H, HE Z H, HUANG D J, et al. Low frequency shadow detection of gas reservoirs in time-frequency domain. Chinese Journal of Geophysics, 2009, 52(1): 215-221. |
| [6] |
王德营, 李振春, 王姣. S域时频滤波分析与改进. 石油物探, 2015, 54(4): 396-403. WANG D Y, LI Z C, WANG J. The analysis and improvement on time-frequency filtering in S-transform domain. Geophysical Prospecting for Petroleum, 2015, 54(4): 396-403. |
| [7] |
高刚, 李玉海, 桂志先, 等. 基于广义S变换频散AVO属性提取方法研究. 岩性油气藏, 2015, 27(4): 84-88. GAO G, LI Y H, GUI Z X, et al. Abstraction of frequency-dependent AVO attributes based on generalized S transform. Lithologic Reservoirs, 2015, 27(4): 84-88. |
| [8] |
陈胜, 欧阳永林, 曾庆才, 等. 匹配追踪子波分解重构技术在气层检测中的应用. 岩性油气藏, 2014, 26(6): 111-114. CHEN S, OUYANG Y L, ZENG Q C, et al. Application of matching pursuit wavelet decomposition and reconstruction technique to reservoir prediction and gas detection. Lithologic Reservoirs, 2014, 26(6): 111-114. |
| [9] |
LI Y D, ZHENG X D. Wigner-Ville distribution and its application in seismic attenuation estimation. Applied Geophysics, 2007, 4(4): 245-254. DOI:10.1007/s11770-007-0034-7 |
| [10] |
MANDIC D P, REHMAN N U, WU Z, et al. Empirical mode decomposition-based time-frequency analysis of multivariate signals:the power of adaptive data analysis. IEEE Signal Processing Magazine, 2013, 30(6): 74-86. DOI:10.1109/MSP.2013.2267931 |
| [11] |
TORRES M E, COLOMINAS M A, SCHLOTTHAUER G, et al. A complete ensemble empirical mode decomposition with adaptive noise. IEEE International Conference on Acoustics, Speech and Signal Processing. IEEE, 2011, 4144-4147. |
| [12] |
BATTISTA B, KNAPP C, MCGEE T, et al. Application of the empirical mode decomposition and Hilbert-Huang transform to seismic reflection data. Geophysics, 2007, 72(2): H29-H37. DOI:10.1190/1.2437700 |
| [13] |
CHEN Y, ZHOU C, YUAN J, et al. Applications of empirical mode decomposition in random noise attenuation of seismic data. Journal of Seismic Exploration, 2014, 23(6): 481-495. |
| [14] |
DRAGOMIRETSKIY K, ZOSSO D. Variational mode decomposition. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544. DOI:10.1109/TSP.2013.2288675 |
| [15] |
GILLES J. Empirical wavelet transform. IEEE Transactions on Signal Processing, 2013, 61(16): 3999-4010. DOI:10.1109/TSP.2013.2265222 |
| [16] |
AUGER F, FLANDRIN P. Improving the readability of timefrequency and time-scale representations by the reassignment method. IEEE Transactions on Signal Processing, 1995, 43(5): 1068-1089. DOI:10.1109/78.382394 |
| [17] |
DAUBECHIES I, LU J, WU H T. Synchrosqueezed wavelet transforms:an empirical mode decomposition-like tool. Applied & Computational Harmonic Analysis, 2011, 30(2): 243-261. |
| [18] |
HERRERA R H, HAN J, MIRKO V D B. Applications of the synchrosqueezing transform in seismic time-frequency analysis. Geophysics, 2014, 79(3): V55-V64. DOI:10.1190/geo2013-0204.1 |
| [19] |
YU G, YU M, XU C. Synchroextracting transform. IEEE Transactions on Industrial Electronics, 2017, 64(10): 8042-8054. DOI:10.1109/TIE.2017.2696503 |
| [20] |
BALCH A H. Color sonagrams:a new dimension in seismic data interpretation. Geophysics, 1971, 36(6): 1074-1098. DOI:10.1190/1.1440233 |
| [21] |
COLEOU T, POUPON M, AZBEL K. Unsupervised seismic facies classification:a review and comparison of techniques and implementation. The Leading Edge, 2003, 22(10): 942-953. DOI:10.1190/1.1623635 |
| [22] |
GAO D. Application of three-dimensional seismic texture analysis with special reference to deep-marine facies discrimination and interpretation:Offshore Angola, west Africa. AAPG Bulletin, 2007, 91(12): 1665-1683. DOI:10.1306/08020706101 |
| [23] |
ROY A, DOWDELL B L, MARFURT K J. Characterizing a Mississippian tripolitic chert reservoir using 3 D unsupervised and supervised multiattribute seismic facies analysis:an example from Osage County, Oklahoma. Interpretation, 2013, 1(2): SB109-SB124. DOI:10.1190/INT-2013-0023.1 |
| [24] |
KOHONEN T. Self-organizing maps. Berlin: Springer-Verlag, 1995.
|
| [25] |
VATANEN T, OSMALA M, RAIKO T, et al. Self-organization and missing values in SOM and GTM. Neurocomputing, 2015, 147(6/7): 60-70. |
| [26] |
GISBRECHT A, HAMMER B. Relevance learning in generative topographic mapping. Neurocomputing, 2011, 74(9): 1351-1358. DOI:10.1016/j.neucom.2010.12.015 |
| [27] |
BISHOP C, SVENSÉN M, WILLIAMS C. GTM:the generative topographic mapping. Neural Computation, 1998, 10(1): 215-234. DOI:10.1162/089976698300017953 |
| [28] |
WALLET B C, MATOS M C D, KWIATKOWSKI J T, et al. Latent space modeling of seismic data:an overview. The Leading Edge, 2009, 28(12): 1454-1459. DOI:10.1190/1.3272700 |
| [29] |
ROY A, ROMERO-PELÁEZ A S, KWIATKOWSKI T J, et al. Generative topographic mapping for seismic facies estimation of a carbonate wash, Veracruz Basin, southern Mexico. Interpretation, 2014, 2(2): SA31-SA47. |
| [30] |
LIU Y. Seismic "low frequency shadows" for gas sand reflection. Denver: SEG, 2004.
|
 2018, Vol. 30
2018, Vol. 30



