2. 中国石油华北油田分公司 勘探开发研究院, 河北 任丘 062552;
3. 中国石化西南油气分公司 川东北采气厂, 四川 阆中 637042
2. Research Institute of Exploration and Development, PetroChina Huabei Oilfield Company, Renqiu 062552, Hebei, China;
3. Northeastern Sichuan Gas Production Plant, Sinopec Southwest Oil and Gas Company, Langzhong 637402, Sichuan, China
随着全球油气资源形势的日益严峻,页岩气、煤层气以及致密砂岩气等非常规天然气资源备受关注,其中以致密气藏的勘探与开发最为成熟,国内在鄂尔多斯盆地苏里格气田以及四川盆地须家河组均已发现较大储量规模的致密气[1-2]。国内外学者对致密气藏渗流机理以及常规压裂水平井产能均进行了较为深入的研究[3-9],且大多侧重于未综合考虑致密气藏非达西渗流条件下压裂水平井非稳态产能模型[10]的研究,但现场实际情况表明,有时受下游销售的影响,气井产量频繁调整,非稳态产能模型并不适用于该类气井产能预测,而将地层流体短期渗流视为稳态渗流更为合理。目前,虽然已有较多的压裂水平井稳态渗流模型,但考虑气水两相渗流条件下的致密气藏压裂水平井稳态渗流模型几乎未见报道。基于致密气藏以及裂缝非达西渗流特征,利用保角变换方法以及势的叠加原理,定义裂缝与储层气水两相广义拟压力,建立致密气藏压裂水平井气水两相产能模型,并利用实例验证模型的准确性,分析各个因素对产水压裂水平井产能的影响,以期为致密气藏压裂水平井裂缝参数优化提供理论支撑。
1 致密气藏气水同产压裂水平井产能公式推导 1.1 物理模型及假设条件图 1为产水致密气藏压裂水平井物理模型,为了研究的需要,对其作如下假设:① 储层水平、均质、等厚、各向同性且顶底边界封闭,厚度为h;② 在气藏未开发之前,地层压力处处相等,为原始地层压力pi,在开发过程中,短时间内地层压力保持不变,为稳态渗流;③ 气藏为气水两相渗流,且气、水两相的渗流均遵循非达西渗流规律;④ 水平段长度为L,位于气藏中部,平行于储层顶、底边界,采用射孔完井方式,且水平段无补孔,气、水两相流体均先进入裂缝,由裂缝流入水平井井筒;⑤ 人工裂缝为横向裂缝,水平井压裂后裂缝沿井筒方向呈等间距、等长度分布,水力裂缝导流能力短期不随时间变化,为恒定值;⑥ 水力压裂后不考虑表皮效应,且忽略重力和毛管压力的影响。

|
下载eps/tif图 图 1 致密气藏压裂水平井物理模型 Fig. 1 Physical model of fractured horizontal well in tight gas reservoir |
(1)地层气水两相渗流模型
图 2为压裂水平井物理模型的俯视图。针对裂缝条数不同的压裂水平井,在图 2中建立了相应的坐标系。

|
下载eps/tif图 图 2 不同裂缝条数下压裂水平井物理模型 Fig. 2 Physical model of fractured horizontal well with different fracture numbers |
对于任意一条横向裂缝,其周围等势线为一簇簇椭圆形,引入如下保角变换函数[11]:
| $ {Z_1} = {X_{\rm{f}}}\cosh {Z_2} $ | (1) |
其中
| $ {Z_1} = x + iy, {Z_2} = u + iv $ |
式中:Xf为裂缝半长,m。通过保角变换,将Z1平面内的上半部分椭圆形变换为Z2平面内宽度为π的右边无限大的平面,将Z1平面下半部分椭圆形变换为Z2平面内宽度为π的左边无限大的平面,并将长度为2 Xf的裂缝变换为宽度为π的排液坑道(图 3)。

|
下载eps/tif图 图 3 裂缝平面保角变换示意图 Fig. 3 Sketch map of conformal mapping in fracture plane |
将式(1)进行实部与虚部分离得到
| $ \left\{ \begin{array}{l} x = {X_{\rm{f}}}{\rm{ch}}\;u\cdot{\rm{ cos}}v\\ y = {X_{\rm{f}}}{\rm{sh}}\;u\cdot{\rm{ sin}}v \end{array} \right. $ | (2) |
根据双曲正、余弦函数的性质,由式(2)得到u关于x,y的表达式为
| $ u=\text{arch}\frac{1}{\sqrt{2}}{{\left[ \frac{X_{\text{f}}^{2}+{{x}^{2}}+{{y}^{2}}}{X_{\text{f}}^{2}}+\sqrt{\frac{{{X}_{\text{f}}}+{{x}^{2}}+{{y}^{2}}}{X_{\text{f}}^{2}}-\frac{4{{x}^{2}}}{X_{\text{f}}^{2}}} \right]}^{0.5}} $ | (3) |
对于Z2平面内的线性渗流,地层中任意一点处的势分布函数为
| $ \Phi = \frac{{1.842{q_{\rm{o}}}}}{h}u + C $ | (4) |
式中:Φ为储层中任意一点的势,mD·MPa·(mPa· s)-1;qo为单条裂缝产量,m3·d-1;h为储层厚度,m;C为常数。
将式(3)代入式(4),得
| $ \Phi = \frac{{1.842{q_{\rm{o}}}}}{h}{\rm{arch}}\sqrt {\frac{{a + \sqrt {a-4c} }}{2}} + C $ | (5) |
其中
| $ a = 1 + c + {y^2} + X_{\rm{f}}^{-2}, c = {x^2}X_{\rm{f}}^{-2} $ |
式(5)的推导基于裂缝中点位于坐标原点,在图 2中,令任意一条裂缝中点坐标为(0,y0),则式(5)可以变换为
| $ \Phi = \frac{{1.842{q_{\rm{o}}}}}{h}{\rm{arch}}\sqrt {\frac{{b + \sqrt {b-4c} }}{2}} + C $ | (6) |
其中
| $ b = 1 + c + {\left( {{y_0}-y} \right)^2}X_{\rm{f}}^{-2} $ |
式(6)即储层条件下,任意一条裂缝周围势的分布,将其变化为压力关系式为
| $ p = \frac{{1.842{q_{\rm{o}}}{\mu _{\rm{o}}}}}{{Kh}}{\rm{arch}}\sqrt {\frac{{b + \sqrt {b-4c} }}{2}} + C $ | (7) |
式中:p为压力,MPa;μo为流体黏度,mPa·s;K为渗透率,mD。
令
| $ {A_1} = {\rm{arch}}\sqrt {\frac{{b + \sqrt {b-4c} }}{2}} $ | (8) |
将式(7)两边同时微分,得
| $ {\rm{d}}p = \frac{{1.842{q_{\rm{o}}}{\mu _{\rm{o}}}}}{{Kh}}{\rm{d}}{A_1} $ | (9) |
根据气水相似渗流原理,可以将式(9)转化为气相渗流方程。同时,在气水两相渗流过程中,水相与气相的生产会在裂缝周围产生不同的压力分布,当仅考虑气相时,裂缝周围产生的压力分布为
| $ $ | (10) |
式中:qg为气相产量,m3·d-1;μg为气相黏度,mPa· s;Krg为气相相对渗透率。当仅考虑水相时,裂缝周围的压力分布为
| $ {\rm{d}}p = \frac{{1.842{q_{\rm{o}}}{\mu _{\rm{o}}}}}{{K \cdot {K_{{\rm{rg}}}}h}}{\rm{d}}{A_1} + C $ | (11) |
式中:qw为水相产量,m3·d-1;μw为水相黏度,mPa· s;Krw为水相相对渗透率。
在实际地层气水两相渗流过程中,裂缝周围的压力分布是气相与水相共同作用的结果,因此,将式(10)与式(11)进一步处理后化简为
| $ \frac{{{K_{{\rm{rg}}}}{\rho _{\rm{g}}}}}{{{\mu _{\rm{g}}}}}{\rm{d}}p = \frac{{1.842{q_{\rm{g}}}{\rho _{\rm{g}}}}}{{Kh}}{\rm{d}}{A_1} + C $ | (12) |
| $ \frac{{{K_{{\rm{rw}}}}{\rho _{\rm{w}}}}}{{{\mu _{\rm{w}}}}}{\rm{d}}p = \frac{{1.842{q_{\rm{w}}}{\rho _{\rm{w}}}}}{{Kh}}{\rm{d}}{A_1} + C $ | (13) |
式中:ρg为气相密度,g· cm-3;ρw为水相密度,g· cm-3。
根据质量守恒定律可得
| $ {q_{\rm{g}}}{\rho _{\rm{g}}} = {q_{{\rm{gscf}}}}{\rho _{{\rm{gsc}}}}, {q_{\rm{w}}}{\rho _{\rm{w}}} = {q_{{\rm{wscf}}}}{\rho _{{\rm{wsc}}}} $ | (14) |
式中:ρgsc为标准状况下气相密度,g·cm-3;ρwsc为标准状况下水相密度,g·cm-3;qgscf为标准状况下气相产量,m3·d-1;qwsc f为标准状况下水相产量,m3·d-1。
将式(14)分别代入式(12)和式(13),并将两式相加,得
| $ \left( {\frac{{{K_{{\rm{rg}}}}{\rho _{\rm{g}}}}}{{{\mu _{\rm{g}}}}} + \frac{{{K_{{\rm{rw}}}}{\rho _{\rm{w}}}}}{{{\mu _{\rm{w}}}}}} \right){\rm{d}}p = \frac{{1.842\left( {{q_{{\rm{gscf}}}}{\rho _{{\rm{gsc}}}}, + {q_{{\rm{wscf}}}}{\rho _{{\rm{wsc}}}}} \right)}}{{Kh}}{\rm{d}}{A_1} + C $ | (15) |
当考虑储层应力敏感以及气体滑脱效应时,K的表达式为
| $ K = {K_{\rm{i}}}\left( {1 + \frac{\delta }{p}} \right){{\rm{e}}^{-\alpha \left( {{p_{\rm{i}}}-p} \right)}} $ | (16) |
式中:Ki为储层绝对渗透率,mD;δ为滑脱系数,MPa;α为敏感性指数,MPa-1;pi为原始地层压力,MPa。
将式(16)代入式(15),等式左右两侧在对应区间上积分,并定义气水两相广义拟压力为
| $ \psi \left( p \right) = \int\limits_{{p_{{\rm{se}}}}}^{{p_{\rm{i}}}} {\left( {\frac{{{K_{{\rm{rg}}}}{\rho _{\rm{g}}}}}{{{\mu _{\rm{g}}}}} + \frac{{{K_{{\rm{rw}}}}{\rho _{\rm{w}}}}}{{{\mu _{\rm{w}}}}}} \right)} \left( {1 + \frac{\delta }{p}} \right){{\rm{e}}^{-\alpha \left( {{p_{\rm{i}}}-p} \right)}}{\rm{d}}p $ | (17) |
将式(17)代入式(15),并定义水气体积比Rwg = qwsc /qgscf,式(15)可进一步变化为
| $ \begin{array}{l} \psi \left( {x, y} \right) = \frac{{1.842\left( {{\rho _{{\rm{gsc}}}} + {R_{{\rm{wg}}}}{\rho _{{\rm{wsc}}}}} \right)}}{{{K_{\rm{i}}}h}} \cdot \\ {q_{{\rm{gscf}}}}\;{\rm{arch}}\sqrt {\frac{{b + \sqrt {b-4c} }}{2}} + C \end{array} $ | (18) |
式(18)即气水两相渗流条件下致密气藏压裂水平井仅考虑单条裂缝生产时,裂缝周围储层中气水两相广义拟压力分布。根据势的叠加原理,得到考虑N条裂缝干扰条件下储层中气水两相广义拟压力分布为
| $ \begin{array}{l} \psi \left( {x, y} \right) = \frac{{1.842\left( {{\rho _{{\rm{gsc}}}} + {R_{{\rm{wg}}}}{\rho _{{\rm{wsc}}}}} \right)}}{{{K_{\rm{i}}}h}} \cdot \\ \sum\limits_{i =-{N_0}}^{{N_0}} {{q_{{\rm{gscf}}i}}{\rm{arch}}} \sqrt {\frac{{b + \sqrt {b-4c} }}{2}} + {C_1} \end{array} $ | (19) |
其中
| $ {N_0} = \left\{ \begin{array}{l} \frac{N}{2}\;\;\;\;\;\;N 为偶数 \\ \frac{{N-1}}{2}\;\;N为奇数 \end{array} \right. $ |
式中:qgscfi为标准状况下第i条裂缝的产量,m3·d-1;C1为常数。
在第j条裂缝处(0, nd),气水两相广义拟压力为
| $ \begin{array}{l} \psi \left( {0, nd} \right) = \frac{{1.842\left( {{\rho _{{\rm{gsc}}}} + {R_{{\rm{wg}}}}{\rho _{{\rm{wsc}}}}} \right)}}{{{K_{\rm{i}}}h}} \cdot \\ \sum\limits_{i =-{N_0}}^{{N_0}} {{q_{{\rm{gscf}}i}}{\rm{arch}}} \sqrt {1 + \frac{{{{\left( {nd-id} \right)}^2}}}{{X_{\rm{f}}^2}}} + {C_1} \end{array} $ | (20) |
式中:d为裂缝间距,m。
在泄气边界处(0, re),气水两相广义拟压力为
| $ \begin{array}{l} \psi \left( {0, {r_{\rm{e}}}} \right) = \frac{{1.842\left( {{\rho _{{\rm{gsc}}}} + {R_{{\rm{wg}}}}{\rho _{{\rm{wsc}}}}} \right)}}{{{K_{\rm{i}}}h}} \cdot \\ \sum\limits_{i =-{N_0}}^{{N_0}} {{q_{{\rm{gscf}}i}}{\rm{arch}}} \sqrt {1 + \frac{{{{\left( {{r_{\rm{e}}}-id} \right)}^2}}}{{X_{\rm{f}}^2}}} + {C_1} \end{array} $ | (21) |
式(21)与式(20)相减,得
| $ \begin{array}{l} {\psi _{\rm{e}}}- {\psi _{{\rm{f}}j}} = \frac{{1.842\left( {{\rho _{{\rm{gsc}}}} + {R_{{\rm{wg}}}}{\rho _{{\rm{wsc}}}}} \right)}}{{{K_{\rm{i}}}h}} \cdot \\ \sum\limits_{i =- {N_0}}^{{N_0}} {{q_{{\rm{gscf}}i}}\left[{{\rm{arch}}\sqrt {1 + \frac{{{{\left( {{r_{\rm{e}}}-id} \right)}^2}}}{{X_{\rm{f}}^2}}}-{\rm{arch}}\sqrt {1 + \frac{{{{\left( {nd-id} \right)}^2}}}{{X_{\rm{f}}^2}}} } \right]} \end{array} $ | (22) |
式中:ψe为泄气边界处拟压力,MPa2·(mPa·s)-1;ψfj为第j条裂缝处拟压力,MPa2·(mPa·s)-1。
根据双曲余弦函数的性质
| $ {\rm{arch}}\sqrt {1 + {x^2}} = \ln \left( {x + \sqrt {1 + {x^2}} } \right) $ | (23) |
式(22)可以变化为
| $ \begin{array}{l} {\psi _{\rm{e}}}-{\psi _{{\rm{f}}j}} = \frac{{1.842\left( {{\rho _{{\rm{gsc}}}} + {R_{{\rm{wg}}}}{\rho _{{\rm{wsc}}}}} \right)}}{{{K_{\rm{i}}}h}} \cdot \\ \sum\limits_{i-{N_0}}^{{N_0}} {{q_{{\rm{gsef}}i}}\ln } \frac{{\left( {\frac{{{r_{\rm{e}}}}}{{{X_{\rm{f}}}}}-\frac{{id}}{{{X_{\rm{f}}}}}} \right) + \sqrt {1 + \frac{{{{\left( {{r_{\rm{e}}} - id} \right)}^2}}}{{X_{\rm{f}}^2}}} }}{{\left| {\frac{{nd}}{{{X_{\rm{f}}}}} - \frac{{id}}{{{X_{\rm{f}}}}}} \right| + \sqrt {1 + \frac{{{{\left( {nd - id} \right)}^2}}}{{X_{\rm{f}}^2}}} }} \end{array} $ | (24) |
(2)裂缝气水两相渗流模型
与单相渗流相同,气水两相渗流条件下裂缝中的渗流仍可以划分为远井筒区域的线性渗流以及近井筒区域的径向渗流。对于线性渗流区域,气、水两相运动方程分别为
| $ \frac{{{\rm{d}}p}}{{{\rm{d}}x}} =-\frac{{11.574{\mu _{\rm{g}}}}}{{{K_{\rm{f}}} \cdot {K_{{\rm{rg}}}}}}{v_{\rm{g}}} $ | (25) |
| $ \frac{{{\rm{d}}p}}{{{\rm{d}}x}} =-\frac{{11.574{\mu _{\rm{w}}}}}{{{K_{\rm{f}}} \cdot {K_{{\rm{rw}}}}}}{v_{\rm{w}}} $ | (26) |
式中:Kf为裂缝渗透率,mD;vg为气相流速,m/s;vw为水相流速,m/s。考虑裂缝应力敏感,根据上述气水两相渗流推导方法同理得到裂缝线性渗流气水两相产能公式为
| $ \left( {\frac{{{K_{{\rm{rg}}}}{\rho _{\rm{g}}}}}{{{\mu _{\rm{g}}}}} + \frac{{{K_{{\rm{rw}}}}{\rho _{\rm{w}}}}}{{{\mu _{\rm{w}}}}}} \right){{\rm{e}}^{-{\alpha _{\rm{f}}}\left( {{p_{\rm{i}}}-p} \right)}}{\rm{d}}p =-\frac{{11.574\left( {{\rho _{{\rm{gsc}}}} + {R_{{\rm{wg}}}}{\rho _{{\rm{wsc}}}}} \right)}}{{2{K_{{\rm{fi}}}}{\rm{d}}x}} \cdot {q_{{\rm{gscf}}j}}{\rm{d}}x $ | (27) |
式中:αf为裂缝压力敏感系数,MPa-1;Kfi为初始条件下考虑滑脱效应的裂缝渗透率,mD;w为裂缝宽度,m。
定义裂缝气水两相拟压力为
| $ \psi \left( p \right) = \int\limits_{{p_{{\rm{sc}}}}}^p {\left( {\frac{{{K_{{\rm{rg}}}}{\rho _{\rm{g}}}}}{{{\mu _{\rm{g}}}}} + \frac{{{K_{{\rm{rw}}}}{\rho _{\rm{w}}}}}{{{\mu _{\rm{w}}}}}} \right)} {{\rm{e}}^{-{\alpha _{\rm{f}}}\left( {{p_{\rm{i}}}-p} \right)}}{\rm{d}}p $ | (28) |
式(27)在对应区间上积分得到
| $ \psi \left( {{p_{{\rm{f}}j}}} \right)-\psi \left( {{p_{{\rm{h}}j}}} \right) = \frac{{5.787\left( {{\rho _{{\rm{gsc}}}} + {R_{{\rm{wg}}}}{\rho _{{\rm{wsc}}}}} \right)\left( {{X_{\rm{f}}}-\frac{h}{2}} \right)}}{{{K_{{\rm{fi}}}}wh}}{q_{{\rm{gscf}}j}} $ | (29) |
式中:ψ(pfj)为第j条裂缝拟压力,MPa· 2(mPa· s)-1;ψ(phj)为第j条裂缝周围线性流区拟压力,MPa2·(mPa·s)-1。
对于径向渗流区域,气水两相运动方程分别为
| $ \frac{{{\rm{d}}p}}{{{\rm{d}}r}} = \frac{{11.574{\mu _{\rm{g}}}}}{{{K_{\rm{f}}} \cdot {K_{{\rm{rg}}}}}}\frac{{{q_{\rm{g}}}}}{{2{\rm{\pi }}rw}} + 1.34 \times {10^{-13}}\beta {\rho _{\rm{g}}}{\left( {\frac{{{q_{\rm{g}}}}}{{2{\rm{\pi }}rw}}} \right)^2} $ | (30) |
| $ \frac{{{\rm{d}}p}}{{{\rm{d}}r}} = \frac{{11.574{\mu _{\rm{w}}}}}{{{K_{\rm{f}}} \cdot {K_{{\rm{rw}}}}}}\frac{{{q_{\rm{w}}}}}{{2{\rm{\pi }}rw}} $ | (31) |
考虑裂缝应力敏感,分别将式(30)和式(31)进一步变化为
| $ \frac{{{K_{{\rm{rg}}}}{\rho _{\rm{g}}}}}{{{\mu _{\rm{g}}}}}{{\rm{e}}^{-{\alpha _{\rm{f}}}\left( {{p_{\rm{i}}}-p} \right)}}{\rm{d}}p = \frac{{1.842{q_{{\rm{gscf}}j}}{\rho _{{\rm{gsc}}}}}}{{{K_{{\rm{fi}}}}w}}\frac{{{\rm{d}}r}}{r} + \frac{{2.59 \times {{10}^{-4}}}}{{K_{{\rm{rg}}}^{0.5}{\mu _{\rm{g}}}}}\frac{{\rho _{{\rm{gsc}}}^2q_{{\rm{gscf}}j}^2}}{{K_{\rm{f}}^{1.5}{w^2}}}\frac{{{\rm{d}}r}}{{{r^2}}} $ | (32) |
| $ \frac{{{K_{{\rm{rw}}}}{\rho _{\rm{w}}}}}{{{\mu _{\rm{w}}}}}{{\rm{e}}^{-{\alpha _{\rm{f}}}\left( {{p_{\rm{i}}}-p} \right)}}{\rm{d}}p = \frac{{1.842{q_{{\rm{wsc}}}}{\rho _{{\rm{wsc}}}}}}{{{K_{{\rm{fi}}}}w}}\frac{{{\rm{d}}r}}{r} $ | (33) |
联立式(32)与式(33),并引入裂缝气水两相拟压力的定义,得
| $ \begin{array}{l} {\psi _{{\rm{h}}j}}-{\psi _{{\rm{wf}}j}} = \frac{{1.842\left( {{\rho _{{\rm{gsc}}}} + {\rho _{{\rm{wsc}}}}{R_{{\rm{wg}}}}} \right){q_{{\rm{gscf}}j}}}}{{{K_{{\rm{fi}}}}w}}\ln \frac{h}{{2{r_{\rm{w}}}}} + \\ \frac{{2.59 \times {{10}^{-4}}\rho _{{\rm{gsc}}}^2q_{{\rm{gscf}}j}^2}}{{K_{{\rm{fi}}}^{1.5}{w^2}}}\int\limits_{{r_{\rm{w}}}}^{\frac{h}{2}} {\frac{{{\rm{d}}r}}{{K_{{\rm{rg}}}^{0.5}{\mu _{\rm{g}}}{r^2}{{\rm{e}}^{-0.5{\alpha _{\rm{f}}}\left( {{p_{\rm{i}}} - p} \right)}}}}} \end{array} $ | (34) |
式中:ψhj为第j条裂缝所在水平井段的径向流区拟压力,MPa2·(mPa·s)-1;ψwfj为第j条裂缝处井筒拟压力,MPa2·(mPa·s)-1;rw为井筒半径,m。式(34)等号右边第2项可采用简化处理方法,即
| $ \int\limits_{{r_{\rm{w}}}}^{\frac{h}{2}} {\frac{{{\rm{d}}r}}{{K_{{\rm{rg}}}^{0.5}{\mu _{\rm{g}}}{r^2}}}} = \frac{1}{{\bar K_{{\rm{rg}}}^{0.5}{{\bar \mu }_{\rm{g}}}{{\rm{e}}^{-0.5{\alpha _{\rm{f}}}\left( {{p_{\rm{i}}}-\bar p} \right)}}}}\left( {\frac{1}{{{r_{\rm{w}}}}}-\frac{2}{h}} \right) $ | (35) |
因此,联立地层气水两相渗流模型和裂缝气水两相渗流模型,可以得到含有2 N个未知数的2 N个非线性方程,并形成相应的非线性方程组,即致密气藏压裂水平井气水两相产能公式。
2 气水两相广义拟压力的求解储层与裂缝两相拟压力的求解思路基本一致,这里仅以储层气水两相广义拟压力的求解为例。联立气水两相运动方程[式(12)、式(13)],得到Krg与Krw 之间的关系为
| $ \frac{{{K_{{\rm{rg}}}}}}{{{K_{{\rm{rw}}}}}} = \frac{1}{{{R_{{\rm{wg}}}}}} \cdot \frac{{{\mu _{\rm{g}}}{B_{\rm{g}}}}}{{{\mu _{\rm{w}}}{B_{\rm{w}}}}} $ | (36) |
式中:Bg和Bw分别为气相和水相体积系数。
将μg与ρg的关系式[12]代入式(36)中,得到如下气水两相广义拟压力的计算步骤:① 利用相渗曲线得到Krg,Krw与含水饱和度Sw的关系,并结合物性参数与压力的关系,迭代求解得到任意压力下的含水饱和度;② 根据步骤① 的结果,结合相渗曲线,求得任何压力下的气水两相相对渗透率Krg,Krw;③ 将积分区间划分为n等份,并结合步骤② 求解结果,利用复化辛普森数值积分方法得到气水两相广义拟压力与压力的函数关系。
3 实例计算及产能影响因素分析A井为四川盆地某致密气藏中一水平井,完井方式为射孔完井。对该井进行加砂压裂后,投产初期不产水,产量保持稳定,投产一段时间后,开始产水,平均日产水气比为1 m3/104 m3,回压试井得到该井无阻流量为4.805 3万m3,通过压敏实验得到岩心人造裂缝应力敏感指数约为0.04 MPa-1,并通过文献调研[13]同类储层同等渗透率条件下裂缝应力敏感指数大小,验证了实验数据的准确性。
利用已知气藏基本参数和压力恢复试井解释参数(表 1),结合储层与裂缝的相渗曲线(图 4、图 5),分别计算考虑各种不同影响因素时该井无阻流量,并与产能测试该井无阻流量(4.805 3万m3·d-1)进行对比(表 2)。
|
|
下载CSV 表 1 气藏基本参数及试井解释参数 Table 1 Parameters of gas reservoir and well test |

|
下载eps/tif图 图 4 储层气水两相相渗曲线 Fig. 4 Relative permeability curves of gas-water two phase in reservoir |

|
下载eps/tif图 图 5 裂缝气水两相相渗曲线 Fig. 5 Relative permeability curves of gas-water two phase in fracture |
|
|
下载CSV 表 2 不同影响因素下无阻流量与产能测试无阻流量对比 Table 2 Contrast of absolute open flow under different influencing factors |
由表 2可知,利用考虑产水+储层与裂缝应力敏感效应的压裂水平井模型计算无阻流量的结果与产能测试无阻流量结果相对误差最小,且在此基础上考虑滑脱效应也与产能测试结果相对误差较小,表明本文模型具有较高的准确性,也说明滑脱效应对压裂水平井产能影响较小;同时,还可以看出,产水、储层应力敏感以及裂缝应力敏感对压裂水平井无阻流量影响均较明显,因此,在实例计算的基础上,有必要进一步分析非达西渗流特征以及裂缝参数对压裂水平井产能的影响。
(1)水气体积比对产能的影响
当其他参数一定时,作生产水气体积比分别为1 m3/104m3,2 m3/104m3,3 m3/104 m3,4 m3/104 m3条件下压裂水平井流入动态曲线(图 6)。从图 6可以看出,随着水气体积比的逐渐增大,气井流入动态曲线逐渐左移,无阻流量逐渐减小,但减小的趋势越来越平缓。这表明,产水使得压裂水平井产能大大降低,因此,在水平井钻完井以及压裂施工过程中,应尽量避开含水层,若无法避免气井见水,则应合理优化气井工作制度,延缓气井见水时间。

|
下载eps/tif图 图 6 水气体积比对压裂水平井产能的影响 Fig. 6 Effect of water-gas volume ratio on productivity of fractured horizontal well |
(2)裂缝条数对产能的影响
当其他参数一定时,作裂缝条数分别为3,5,7,9条件下压裂水平井流入动态曲线(图 7)。从图 7可以看出,随着裂缝条数的逐渐增加,气井流入动态曲线逐渐右移,无阻流量逐渐增大,但增大的趋势越来越平缓。这是由于在水平井长度相同条件下,裂缝条数越多,裂缝间距就越小,裂缝之间的干扰也就越强,故无阻流量随裂缝条数的变化呈现非线性变化特征。因此,在作水平井压裂设计时,应合理优化裂缝条数,达到经济效益以及产量的最优化。

|
下载eps/tif图 图 7 裂缝条数对压裂水平井产能的影响 Fig. 7 Effect of fracture numbers on productivity of fractured horizontal well |
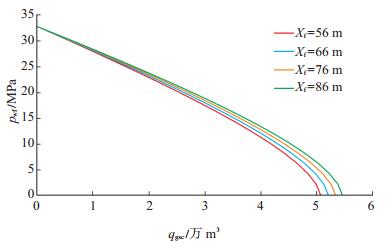
(3)裂缝半长对产能的影响
当其他参数一定时,作裂缝半长分别为56 m,66 m,76 m,86 m条件下压裂水平井流入动态曲线(图 8)。从图 8可以看出,随着裂缝半长逐渐增大,气井流入动态曲线逐渐右移,无阻流量逐渐增大。这是由于裂缝半长越长,裂缝所提供的渗流面积越大。因此,在作水平井压裂设计时,在考虑经济效益的前提下应尽量增大裂缝长度,以达到压裂效果的最优化。
|
下载eps/tif图 图 8 裂缝半长对压裂水平井产能的影响 Fig. 8 Effect of fracture half-length on productivity of fractured horizontal well |
(4)裂缝导流能力对产能的影响
当其他参数一定时,考虑裂缝导流能力与地层压力短期内不随时间变化,作裂缝导流能力分别为100 mD·m,200 mD·m,300 mD·m,400 mD·m条件下压裂水平井流入动态曲线(图 9)。从图 9可以看出,随着裂缝导流能力增强,气井流入动态曲线右移,无阻流量增大,但增大的趋势越来越平缓。然而,从总体上看,裂缝导流能力对无阻流量的影响较小,在正常生产压差条件下,其影响几乎可以忽略不计。因此,在水平井压裂设计中,裂缝导流能力并不是影响压裂效果的最重要参数,可在考虑其他参数优化的前提下再对其进行优化。

|
下载eps/tif图 图 9 裂缝导流能力对压裂水平井产能的影响 Fig. 9 Effect of fracture conductivity on productivity of fractured horizontal well |
(5)储层应力敏感指数对产能的影响
当其他参数一定时,作储层应力敏感指数分别为0 MPa-1,0.005 MPa-1,0.010 MPa-1,0.015 MPa-1条件下压裂水平井流入动态曲线(图 10)。从图 10可以看出,考虑储层应力敏感较不考虑储层应力敏感条件下气井流入动态曲线更加靠左,无阻流量较小,且随着储层应力敏感指数的逐渐增大,气井流入动态曲线左移,无阻流量减小,特别是当井底流压较小时,储层应力敏感指数对产能的影响更加明显。因此,在气井生产过程中,应合理优化气井生产压差,削弱储层应力敏感,达到产量的最优化。

|
下载eps/tif图 图 10 储层应力敏感指数对压裂水平井产能的影响 Fig. 10 Effect of reservoir stress sensitivity index on productivity of fractured horizontal well |
(6)裂缝应力敏感指数对产能的影响
当其他参数一定时,作裂缝应力敏感指数分别为0 MPa-1,0.04 MPa-1,0.08 MPa-1,0.12 MPa-1条件下压裂水平井流入动态曲线(图 11)。从图 11可以看出,考虑裂缝应力敏感较不考虑裂缝应力敏感条件下气井流入动态曲线更加靠左,无阻流量较小,且随着裂缝应力敏感指数的逐渐增大,无阻流量逐渐减小,且减小的趋势逐渐增强,特别是当井底流压较小时,裂缝应力敏感指数对产能的影响更加明显。因此,在作水平井压裂设计时,应合理选择支撑剂类型并控制气井生产压差,削弱裂缝应力敏感现象,增大气井产量。

|
下载eps/tif图 图 11 裂缝应力敏感指数对压裂水平井产能的影响 Fig. 11 Effect of fracture stress sensitivity index on productivity of fractured horizontal well |
(1)在常规压裂水平井产能研究的基础上,结合致密气藏非达西渗流特征以及气井产水的影响,考虑裂缝有限导流且短期导流能力为定值,建立了致密气藏压裂水平井气水两相产能计算方法。利用本文方法计算的无阻流量与产能测试无阻流量误差较小,证明了本文方法具有较高的准确性。
(2)致密气藏产水压裂水平井无阻流量随着裂缝条数、裂缝半长及裂缝导流能力的增大而增大,但是裂缝半长和裂缝导流能力对气井产能影响均较小;随着水气体积比、储层以及裂缝应力敏感指数逐渐增大,气井无阻流量减小,特别是水气体积比和裂缝应力敏感指数对压裂水平井产能影响均较明显。滑脱效应对气井产能影响较小,可忽略不计。
| [1] |
邱中建, 邓松涛.
中国非常规天然气的战略地位. 天然气工业, 2012, 32(1): 1–5.
QIU Z J, DENG S T. 2012. Strategic position of unconventional natural gas in China. Natural Gas Industry, 2012, 32(1): 1-5. |
| [2] |
李书恒, 方国庆, 杨金龙, 等.
鄂尔多斯盆地超低渗透储层成因研究及意义. 岩性油气藏, 2012, 24(6): 32–37.
LI S H, FANG G Q, YANG J L, et al. 2012. Origin of ultra-low permeability reservoirs in Ordos Basin and its significance. Lithologic Reservoirs, 2012, 24(6): 32-37. |
| [3] |
王拓, 朱如凯, 白斌, 等.
非常规油气勘探、评价和开发新方法. 岩性油气藏, 2013, 25(6): 35–39.
WANG T, ZHU R K, BAI B, et al. 2013. New methods for the exploration, evaluation and development of unconventional reservoirs. Lithologic Reservoirs, 2013, 25(6): 35-39. |
| [4] |
高树生, 叶礼友, 熊伟, 等.
大型低渗致密含水气藏渗流机理及开发对策. 石油天然气学报(江汉石油学院学报), 2013, 35(7): 93–99.
GAO S S, YE L Y, XIONG W, et al. 2013. Seepage mechanism and strategy for development of large and low permeability and tight sandstone gas reservoirs with water content. Journal of Oil and Gas Technology(Journal of Jianghan Petroleum Institute), 2013, 35(7): 93-99. |
| [5] |
杨朝蓬, 沙雁红, 刘尚奇, 等.
苏里格致密砂岩气藏单相气体渗流特征. 科技导报, 2014, 32(增刊2): 54–58.
YANG Z P, SHA Y H, LIU S Q, et al. 2014. Flow behavior of singlephase gas in Sulige tight sandstone gas reservoir. Science & Technology Review, 2014, 32(28/29): 54-58. |
| [6] |
GUO G, EVANS R D. Inflow performance of a horizontal well intersecting natural fractures. SPE 25501, 1993.
|
| [7] |
郎兆新, 张丽华, 程林松.
压裂水平井产能研究. 石油大学学报, 1994, 18(2): 43–46.
LANG Z X, ZHANG L H, CHENG L S. 1994. Investigation on productivity of fractured horizontal well. Journal of the University of Petroleum, 1994, 18(2): 43-46. |
| [8] |
宁正福, 韩树刚, 程林松, 等.
低渗透油气藏压裂水平井产能计算方法. 石油学报, 2002, 23(2): 68–71.
NING Z F, HAN S G, CHENG L S, et al. 2002. Productivity calculation method of fractured horizontal wells in low permeability oil or gas field. Acta Petrolei Sinica, 2002, 23(2): 68-71. DOI:10.7623/syxb200202015 |
| [9] |
ZHU D, MAGALHAES F, VALKO P P.
2007. Predicting productivity of multiple-fractured horizontal gas wells. SPE 106280, 2007.
|
| [10] |
曾凡辉, 程小昭, 郭建春.
裂缝面非均匀流入的低渗透油藏压裂水平井非稳态产量计算. 中南大学学报(自然科学版), 2016, 47(4): 1353–1358.
ZENG F H, CHENG X Z, GUO J C. 2016. Calculation of unsteady productivity of fractured horizontal wells. Journal of Central South University(Science and Technology), 2016, 47(4): 1353-1358. DOI:10.11817/j.issn.1672-7207.2016.04.035 |
| [11] |
郑松青.
非均匀分段压裂水平井产能计算. 东北石油大学学报, 2013, 37(4): 55–59.
ZHENG S Q. 2013. Productivity calculation of non-uniform multifractured horizontal wells. Journal of Northeast Petroleum University, 2013, 37(4): 55-59. |
| [12] |
陈元千.
确定天然气物性的相关经验公式. 新疆石油地质, 1989, 10(2): 48–55.
CHEN Y Q. 1989. Empirical formulas to determine the petrophysical property of natural gas. Xinjiang Petroleum Geology, 1989, 10(2): 48-55. |
| [13] |
于忠良, 熊伟, 高树生, 等.
致密储层应力敏感性及其对油田开发的影响. 石油学报, 2007, 28(4): 95–98.
YU Z L, XIONG W, GAO S S, et al. 2007. Stress sensitivity of tight reservoir and its influence on oilfield development. Acta Petrolei Sinica, 2007, 28(4): 95-98. DOI:10.7623/syxb200704019 |
 2017, Vol. 29
2017, Vol. 29



