分形理论被誉为大自然的几何学，主要反映复杂形体占有空间的有效性。据文献[1]报道，分形几何的概念由Mandelbrot在1977年正式提出，目前在数学、物理、材料及地质等多个领域均得到了广泛应用。分形理论可以用于描述地质体的结构，也可以作为微观尺度下复杂地质体不规则性的量度，反映地质体微观形态的有序性和复杂程度（研究尺度偏微观）^[2]。随着压汞、吸附及核磁共振（NMR）等先进实验测试技术的不断深入，利用该理论从纳米层次重新认识复杂变形地质体已成为可能^[3]。目前，世界范围内成熟的油气地质理论，如构造地质学、地质力学及沉积学等多偏向于宏观理论，主要评价的是地质体的复杂性，即客观地质现象，但随着非常规油气地质学的快速发展，人们的认识逐渐从唯物到唯象再到唯理发生转变，纳米微观地质学研究的重要性逐步凸显^[4]。微观地质学主要评价的是地质体的趋同性，探讨的是事物的本质。从宏观表象出发，对地质现象提出假设，探讨地质体客观分布规律，同时结合微观地质学研究，揭露事物本质，是未来地质学领域的发展方向。

作为一门成熟理论，将分形应用于油气地质学领域，前人曾做过许多研究，且主要体现在孔隙结构、节理或裂缝的定量表征及微观图像观察等方面。如，张宪国等^[5]利用分形原理将塔南凹陷白垩系低渗透储层孔隙结构划分为4类；姜文等^[6]研究了高变质石煤分形维数对煤岩煤质参数及孔渗的影响；赖锦等^[7]分析了川中须家河组致密砂岩储层分形维数与排驱压力及分选因数之间的关系；Yao等^[8]详细研究了不同变质程度煤岩储层分形维数值变化规律；王刚等^[9]构建了考虑分形特征的节理面渗流计算模型；杨军等^[10]借助于原子力显微镜，利用分形维数对沥青的“蜂状”结构进行了定量分析，而对砂岩、煤岩及页岩（这3类岩石代表了从常规储层岩石到非常规储层岩石的转变^[9-13]）的分形特征研究相对较少。因此，利用压汞、核磁共振及N₂吸附实验结果对砂岩、煤岩及页岩的分形维数进行对比研究，探讨不同类型岩石分形特征参数对渗透率的影响，建立等效毛管迂曲度模型，利用分形理论模型完成对岩石渗透率的预测，以期为深入认识不同类型储层岩石渗流机理提供依据。

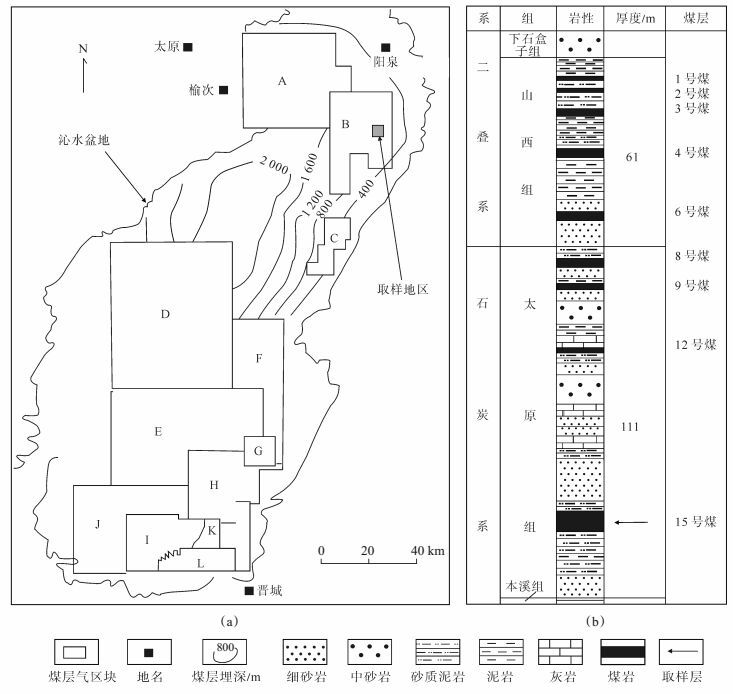
砂岩和页岩样品的测试数据分别来自参考文献[14-15]，测试严谨，结果可靠。其中，砂岩样品取自河南省东北部文留油田东濮凹陷沙河街组，共计24组，编号分别为CS1~CS23和CS25，样品埋藏深度为3 332~3 738 m^[14]；页岩样品取自四川盆地下寒武统牛蹄塘组，它是目前中国页岩气勘探开发潜力最大的层系，样品共计8组，编号分别为Y1~Y4，Y6，Y8~Y9和Y11^[15]；煤岩样品取自和顺煤层气区块太原组。和顺区块构造上位于沁水盆地东北部地区[图 1（a）]，地层整体为单斜构造，倾角15°左右，断裂不发育^[16]。区块内太原组含煤4~9层，含煤平均总厚度为7.43 m，煤岩样品均取自太原组15号煤层[图 1（b）]，为贫煤。该煤层在区内厚度大，分布稳定，埋藏深度为300~400 m，厚度为5 m左右，R_o为1.8%~2.5%，为原生结构煤，样品编号为M1~M7，共计7组。

图 1

Fig. 1

下载eps/tif图 图 1 煤岩样品位置（a）及含煤地层剖面（b） A.寿阳区块；B.和顺区块；C.下黄岩区块；D.沁源区块；E.沁南区块；F.夏店区块；G.长子区块；H.柿庄区块；I.郑庄区块；J.马必区块；K.樊庄区块；L.潘庄区块 Fig. 1 Sampling location of coal samples(a)and coal-bearing strata section(b)

本次研究对砂岩样品进行了压汞及NMR测试，其中压汞曲线通过透水板法获得^[16]。NMR测试使用MARAN7测试仪器完成，拉莫尔频率为7.05 MHz。利用Quadrasorb TM SI比表面积分析仪和孔隙大小分析仪对页岩样品进行了N₂等温吸附测试，吸附-解吸等温线的相对压力为0.01~0.98 MPa。砂岩及页岩样品信息、测试参数及实验操作步骤详见文献[14-15]。煤岩压汞测试实验采用的仪器型号为AutoPore Ⅳ 9500自动压汞仪，实验步骤依据的是国家标准GB/T 21650.1—2008，该仪器具有快速的升压速率、灵活可控的真空系统，以及高性能的低压和高压系统。具体测试条件为：汞的表面张力为480 mN/m，汞接触角为140°，实际测量最大压力为228 MPa，孔径测量为0.003 8~1 000.000 0 mD，有1个高压站和2个低压站。压汞曲线可以反映孔喉（连通性）的结构特征。在压汞实验过程中，进汞过程就是用非润湿相驱替润湿相，当注入压力增加到突破更细小的孔喉毛管压力时，进汞饱和度逐渐增大。

本次研究利用压汞法来测试贫煤样品的压汞特征参数（表 1）。如果煤储层的孔喉均值（Ф）较大（小孔居多），分选差（分选值大），歪度偏负值（对于煤岩储层，其歪度值趋近于0时孔喉配比关系较好），变异系数值偏小，表明煤储层的孔喉配比较差，小孔居多。根据煤岩样品统计，喉道半径小于100 nm的入汞量所对应的孔隙空间占总孔隙空间的77%~90%，其中喉道半径小于10 nm的入汞量所对应的孔隙空间占总孔隙空间的65%~83%。煤岩样品中微小孔隙所占体积百分比较大，渗透率较低，孔喉配置关系为微孔-微喉型。

表 1(Table 1)

表 1 测试煤岩样品的压汞特征参数 Table 1 Mercury injection characteristic parameters of coal samples 编号 取样深度/m 压汞特征参数 孔喉均值 分选值 歪度 变异系数 M1 320 15.674 2.659 -2.145 0.170 M2 300 15.962 2.573 -2.779 0.161 M3 365 14.807 3.646 -1.394 0.246 M4 340 14.851 3.410 -1.634 0.230 M5 355 16.031 1.962 -2.074 0.122 M6 370 16.785 3.876 -2.891 0.133 M7 390 16.892 3.931 -2.913 0.121

下载CSV 表 1 测试煤岩样品的压汞特征参数 Table 1 Mercury injection characteristic parameters of coal samples

岩石类型不同其分形特征也不同。压汞测试通常仅能确定孔径大于3.8 nm的孔隙结构特征，而N₂吸附法可确定孔径小于1 nm的岩石孔隙结构特征^[16]。岩石中流体的渗流能力主要与孔径大于100 nm的孔隙有关，而孔径小于100 nm的孔隙多为吸附孔^[18]。因此，基于压汞及吸附测试的岩石分形特征，可以很好地描述常规砂岩储层，而对于煤岩及页岩储层来说，虽然孔径小于10 nm的孔隙占较大比例，但多为吸附孔，对岩石储层的渗流能力影响较小^[19]。因此，利用上述实验可确定出岩石的分形特征参数，从而探讨分形特征参数对岩石渗透率的影响。

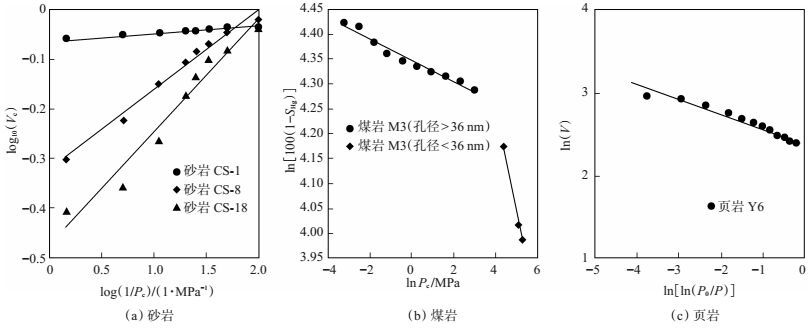
利用压汞法测试结果，可确定砂岩和煤岩样品的分形特征参数；利用N₂吸附法测试结果，可确定页岩的分形特征参数。根据累积孔隙体积（V_c）与入汞压力（p_c）对数值之间的关系，可确定砂岩样品的分形维数（D_f）^[14] [图 2（a）]，取D_f为1~3；根据入汞量（S_Hg）对数值与入汞压力对数值之间的关系，可确定煤岩样品的分形维数[图 2（b）]。这2种方法都可根据入汞量及入汞压力确定岩石的分形维数，并且结果一致。

图 2

Fig. 2

下载eps/tif图 图 2 砂岩、煤岩、页岩样品的分形维数及拟合效果 Fig. 2 Fractal dimension and fitting characteristics of sandstone, coal and shale samples

对于砂岩样品，因岩石孔径较大，在压汞测试孔径范围时，必须对测试数据进行整体拟合，拟合后的线性特征明显，因此所确定的分形维数是可靠的[图 2（a）]。

对于煤岩样品，在对数据进行整体拟合时，其线性拟合效果差，而在孔径为36 nm处进行分段拟合时，则具有较好的线性拟合效果[图 2（b）]。因此，将孔径大于36 nm段测试数据拟合获得的煤岩分形维数定义为D_f1，将孔径小于36 nm段测试数据拟合获得的煤岩分形维数定义为D_f2，D_f1＞D_f2[ 图 2（b）]。同时，求取岩石的毛管平均迂曲度的分形维数（D_T），其取值范围为1＜D_T＜3，计算公式^[20]为

式中：D_T为毛管平均迂曲度的分形维数；T_av为毛管的平均迂曲度；r_av为平均毛管半径，μm；L_m为一个用于表征二维空间毛管特征长度的系数。其中，后3个参数的表达式^[20-22]分别为

式中：φ为孔隙度，%；r_min为最小孔喉半径，μm；r_max为最大孔喉半径，μm；D_f为岩石样品的分形维数。

对于页岩样品，根据平衡压力条件下吸附气体积（V）对数值与相对压力（p0/p，p0为饱和蒸汽压，p为平衡压力）对数值之间的关系，可确定出分形维数，并且数据整体拟合效果较好^[16] [图 2（c）]。根据压汞及N₂吸附测试可确定砂岩、煤岩及页岩的分形特征参数（表 2，表中r_ave为平均孔喉半径）。

表 2(Table 2)

表 2 砂岩、煤岩、页岩样品的分形特征参数 Table 2 Fractal characteristics parameters of sandstone, coal and shale samples 编号 岩性 Df DT rmin /μm rave /μm φ / % K/mD 测试方法 备注 CS1 砂岩 2.984 1.395 0.123 0 0.245 0 12.50 0.129 0 压汞法 据文献[14] CS2 砂岩 2.986 1.214 0.123 0 1.935 0 16.60 18.279 0 压汞法 据文献[14] CS3 砂岩 2.984 1.207 0.123 0 2.303 0 17.00 25.056 0 压汞法 据文献[14] CS4 砂岩 2.698 1.266 0.123 0 3.505 0 16.20 60.502 0 压汞法 据文献[14] CS5 砂岩 2.803 1.257 0.123 0 3.172 0 16.30 45.680 0 压汞法 据文献[14] CS6 砂岩 2.802 1.740 0.123 0 0.151 0 13.70 0.081 0 压汞法 据文献[14] CS7 砂岩 2.821 1.645 0.123 0 0.186 0 13.90 0.130 0 压汞法 据文献[14] CS8 砂岩 2.837 1.545 0.123 0 0.246 0 14.70 0.227 0 压汞法 据文献[14] CS9 砂岩 2.829 1.529 0.123 0 0.307 0 13.20 0.364 0 压汞法 据文献[14] CS10 砂岩 2.878 1.478 0.123 0 0.307 0 14.30 0.432 0 压汞法 据文献[14] CS11 砂岩 2.832 1.459 0.123 0 0.366 0 15.60 0.624 0 压汞法 据文献[14] CS12 砂岩 2.903 1.365 0.123 0 0.599 0 15.00 1.297 0 压汞法 据文献[14] CS13 砂岩 2.792 1.311 0.123 0 1.224 0 17.40 7.050 0 压汞法 据文献[14] CS14 砂岩 2.769 1.312 0.123 0 1.367 0 16.90 5.961 0 压汞法 据文献[14] CS15 砂岩 2.794 1.376 0.123 0 0.750 0 15.70 1.878 0 压汞法 据文献[14] CS16 砂岩 2.811 1.331 0.123 0 1.436 0 14.00 9.006 0 压汞法 据文献[14] CS17 砂岩 2.795 1.329 0.123 0 1.959 0 12.60 10.919 0 压汞法 据文献[14] CS18 砂岩 2.774 1.274 0.123 0 2.321 0 16.90 23.651 0 压汞法 据文献[14] CS19 砂岩 2.903 1.655 0.123 0 0.181 0 9.20 0.043 0 压汞法 据文献[14] CS20 砂岩 2.822 1.275 0.123 0 2.153 0 16.40 14.286 0 压汞法 据文献[14] CS21 砂岩 2.905 1.351 0.123 0 1.402 0 10.50 3.591 0 压汞法 据文献[14] CS22 砂岩 2.945 1.601 0.123 0 0.159 0 9.90 0.046 0 压汞法 据文献[14] CS23 砂岩 2.962 1.310 0.123 0 0.949 0 13.10 2.217 0 压汞法 据文献[14] CS25 砂岩 2.984 1.575 0.123 0 0.123 0 7.90 0.017 0 压汞法 据文献[14] M1 煤岩 2.750 1.279 0.036 0 1.900 0 11.35 0.008 9 压汞法 本文（Df 2；DT2） M2 煤岩 2.841 1.236 0.036 0 1.950 0 14.24 0.009 6 压汞法 本文（Df 2；DT2） M3 煤岩 2.786 1.244 0.036 0 2.000 0 14.04 0.219 2 压汞法 本文（Df 2；DT2） M4 煤岩 2.378 1.352 0.036 0 2.550 0 7.60 0.111 1 压汞法 本文（Df 2；DT2） M5 煤岩 2.909 1.243 0.036 0 1.750 0 12.67 0.001 1 压汞法 本文（Df 2；DT2） M6 煤岩 2.867 1.256 0.036 0 2.100 0 10.00 0.000 9 压汞法 本文（Df 2；DT2） M7 煤岩 2.891 1.254 0.036 0 2.100 0 9.00 0.000 7 压汞法 本文（Df 2；DT2） Y1 页岩 2.693 1.702 0.003 8 0.009 9 8.20 0.000 9 吸附法 据文献[15] Y2 页岩 2.769 2.030 0.003 8 0.006 7 1.80 0.000 6 吸附法 据文献[15] Y3 页岩 2.710 1.930 0.003 8 0.008 6 2.79 0.000 7 吸附法 据文献[15] Y4 页岩 2.722 1.668 0.003 8 0.009 1 9.85 0.000 7 吸附法 据文献[15] Y6 页岩 2.825 2.146 0.003 8 0.004 7 1.26 0.000 3 吸附法 据文献[15] Y8 页岩 2.698 1.724 0.003 8 0.010 0 7.20 0.000 6 吸附法 据文献[15] Y9 页岩 2.787 2.187 0.003 8 0.003 8 2.40 0.000 4 吸附法 据文献[15] Y11 页岩 2.732 2.029 0.003 8 0.008 4 1.35 0.000 7 吸附法 据文献[15]

下载CSV 表 2 砂岩、煤岩、页岩样品的分形特征参数 Table 2 Fractal characteristics parameters of sandstone, coal and shale samples

从表 2可以看出：24组砂岩样品的孔隙度为7.9%~17.4%，平均为14.15%；渗透率为0.017~60.500 mD，平均为9.64 mD；D_f为2.698~2.986，平均为2.859；D_T为1.207~1.74，平均为1.408；D_f＞D_T。7组煤岩样品的孔隙度为7.6%~14.24%，平均为11.27%；渗透率为0.000 7~0.219 2 mD，平均为0.050 2 mD；D_f1为2.954~2.984，平均为2.970；D_f2为2.378~2.909，平均为2.775；D_T1为1.197~1.27，平均为1.230；D_T2为1.236~1.352，平均为1.266；D_f1，f2＞D_T1，T2。8组页岩样品孔隙度为1.26%~9.85%，平均为4.36%；渗透率为0.000 32~0.000 89 mD，平均为0.000 6 mD；D_f为2.693~2.925，平均为2.742；D_T为1.668~2.187，平均为1.927；D_f＞D_T。

砂岩和煤岩样品的分形维数均由压汞法获得，但压汞法并不适合页岩，这是由于页岩具有特低孔、特低渗特征，而且孔隙空间以孔径小于5 nm的孔隙为主^[23]。从计算的砂岩及煤岩的分形维数可以看出，砂岩D_f的平均值为2.859，小于煤岩D_f1的平均值（2.968），但大于煤岩D_f2的平均值（2.733）。岩石的分形维数（D_f）主要反映岩石的非均质性、孔喉分布及孔隙表面粗糙程度等，该值越大，表明岩石孔隙结构越复杂，非均质性越强^[17]。煤岩的D_f1值非常大，接近3，其所对应的岩石孔径大于36 nm，表明该孔径范围内，煤岩内部孔隙结构特征极为复杂，非均质性明显强于常规砂岩储层。煤岩的D_f2平均值要小于砂岩，其所对应的煤岩孔径小于36 nm，表明在该孔径范围内，与煤岩内部孔隙结构特征相比砂岩内部的颗粒排列方式更为规则。

对于页岩样品，压汞法并不能很好地探测孔隙结构，N₂吸附法相比压汞法具有特定优势^[15]。利用该方法确定的页岩样品的分形维数相比煤岩和砂岩要小一些。原因是：与N₂吸附法测试的页岩孔径下限较小有关，较小的孔径范围内岩石的D_f值通常较小。如煤岩D_f2平均为2.733，明显小于D_f1平均值（2.968），但煤岩的D_f2平均值与测试页岩的D_f平均值（2.742）相近。

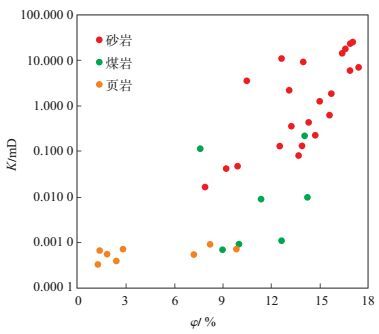
砂岩、煤岩及页岩共计39组岩石样品的渗透率与孔隙度之间的关系如图 3所示。砂岩具有相对较高的孔隙度和渗透率，煤岩次之，页岩最低。测试数据显示渗透率与孔隙度之间具有较好的正相关性，表明孔隙度是控制渗透率的重要因素，但仅利用孔隙度并不能对岩石渗透率进行高精度预测^[20-21]。

图 3

Fig. 3

下载eps/tif图 图 3 砂岩、煤岩及页岩样品的渗透率（K）与孔隙度（φ）关系 Fig. 3 Relationship between permeability and porosity of sandstone, coal and shale samples

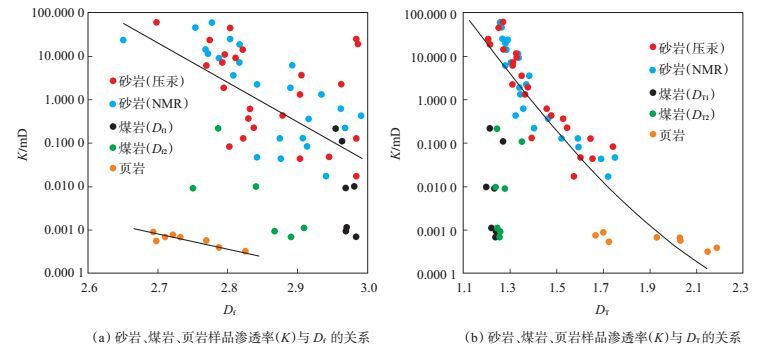
砂岩、煤岩、页岩渗透率与D_f和D_T均具有一定的负相关性（图 4）。砂岩、煤岩、页岩的D_f为2.6~3.0，具有相互重叠的区域[图 4（a）]；渗透率与煤岩D_f1的相关性明显好于与煤岩D_f2的相关性，表明控制该煤岩储层渗透性的孔隙主要为孔径大于36 nm的孔隙，而小于该尺度范围的孔隙主要为吸附孔，对煤储层中流体渗流能力的影响相对较小[图 4（a）]。

图 4

Fig. 4

下载eps/tif图 图 4 分形特征参数对岩石渗透率的影响 Fig. 4 Influences of fractal characteristic parameters on rock permeability

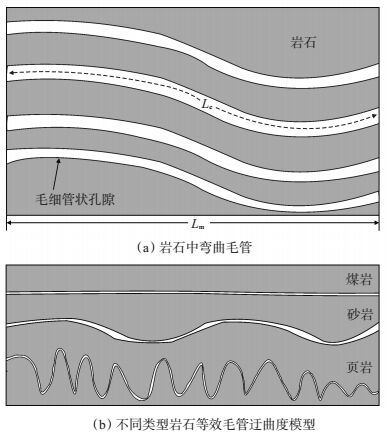
D_T主要反映了岩石中毛管平均迂曲度的微观结构特征。Carman^[24]通过假设岩石内部相互连通的孔隙形态为毛管状，提出了毛管迂曲度（τ）的概念，并将流体流过岩石孔隙的有效流动路径（L_e）与岩心总长度（L_m）的比值，定义为毛管迂曲度，因此为有效值[图 5（a）]。该假设对于常规中—高孔（φ＞10%）砂岩储层均适用^[25]。对于煤岩样品，由于其为原生结构煤，受构造影响较小，岩心尺度裂缝不发育；煤岩中储集空间以近圆形孔隙团为主，微裂隙发育程度较低，因此该假设也适用。对于页岩样品，主要孔隙类型为纳米级微孔^[16]，孔隙间通过喉道连接，因此上述假设也同样适用。

图 5

Fig. 5

下载eps/tif图 图 5 岩石中的弯曲毛管路径 Fig. 5 Bend capillary path diagram in core

从砂岩、煤岩、页岩的D_T与K交会关系[图 4（b）]可以看出：测试数据整体具有较好的负相关性，测试样品的D_T主要为1.1~2.3；不同岩石的D_T值大小具有一定差异，页岩的D_T值相对较大，砂岩次之，煤岩相对较小；D_T值越大，表明岩石中毛管状孔隙的连通性及路径分布越复杂，相应毛管迂曲度越大，流体渗流通过毛管所经过的路径越长，渗透率越低。

对于煤岩，如果D_T值较小，表明煤岩的毛管迂曲度较小；如果D_f值较大，表明煤岩的微观孔隙结构及内部矿物排列方式极为复杂，这是造成渗透率低的重要原因^[26]。姜文等^[6]研究表明，对煤岩渗流能力起最大作用的渗流孔的分形维数随迂曲度的增加而增大，渗透率越低，储层岩石迂曲度及渗流孔分形维数就越大，表明可以利用毛管迂曲度分形维数定量表征岩石的渗透率。

对于页岩，如果D_f值较小，表明纳米级孔隙的分布规律较规则，这主要是由于趋向于纳米级的微观孔隙具有一定的趋同性；如果D_T值较大，表明页岩的毛管迂曲度较大，流体渗流所需的路径较长。

同时，页岩内部微观孔隙及喉道极为细小，流体渗流时遇到较大的毛管阻力，这是造成渗透率极低的重要原因（已达到nD级^[27]）。对于部分具有较好物性的页岩，通常也具有较差的渗透性。如澳大利亚Muderong页岩，平均孔隙度为17%，渗透率却只有1 nD^[28]，复杂的渗流通道是造成Muderong页岩渗透率极低的主要原因（毛管迂曲度非常大）。

对于砂岩，受不同沉积、成岩演化的影响，岩石内部矿物组分差异较大，因而D_f值变化范围也较大^[29]。砂岩的D_T值大于煤岩而小于页岩，这表明砂岩毛管迂曲度大于煤岩，而小于页岩，砂岩较高的渗透率一方面受毛管迂曲度的影响，另一方面也受孔隙度较高的影响。据此，可建立不同类型岩石等效毛管迂曲度模型[图 5（b）]。

具有较小分形维数（D_f及D_T）的砂岩渗透率相对较高。从图 4可以看出，虽然煤岩的孔隙结构复杂程度要高于砂岩[图 4（a），煤岩D_f＞砂岩D_f]，但随着砂岩D_T值的增加[图 4（b）]，有部分砂岩的渗透率要低于煤岩，而渗透率却远远高于页岩，表明毛管迂曲度是影响岩石渗透率最主要的因素。

分形维数所反映的岩石微观孔隙结构特征对岩石渗透率具有影响，因此，可以根据所求取的分形维数及岩石孔喉参数对渗透率进行估算。文献[30]推导了利用分形理论计算岩石渗透率的方法，给出了岩石渗透率的一般表达式^[30]，即

式中：β为常数。当岩石中孔隙为立方体时，β = 1；当孔隙为球体时，β = 4 π/3。本文取β = 4 π/3。

岩石最大孔喉半径值要略大于平均孔喉半径（r_ave）值，若r_max值较大，则r_ave值也相对较大，两者具有一定的对应性。因此，将式（5）中的r_max值用相应各组样品中的r_ave值代替，避免了随机取值的不足，最终预测的渗透率会产生一个系统误差，预测的结果需要进行校正。

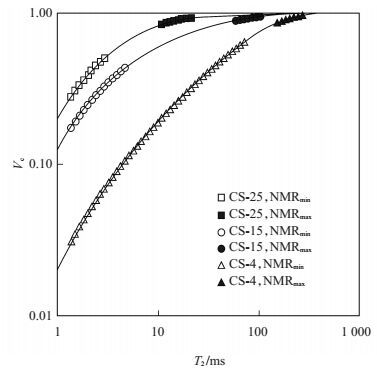
砂岩、煤岩、页岩样品的渗透率校正方程及相关系数如表 3所列。其中，将NMR测试数据根据T2谱时间的大小划分成2段（图 6），较大T2谱所对应的测试数据定义为NMRmax，较小T₂谱所对应的测试数据定义为NMRmin^[14]，利用该校正方程可实现各组岩石样品的渗透率预测，最终预测结果如图 7所示。

表 3(Table 3)

表 3 砂岩、煤岩、页岩样品的渗透率校正方程 Table 3 Permeability modification equation of sandstone, coal and shale samples 岩性 测试法 校正方程 相关系数 砂岩 压汞法 y= 447.20 x + 2.012 0 R2= 0.888 砂岩 NMRmax y = 473.10 x + 0.201 0 R2= 0.976 砂岩 NMRmin y = 329.20 x + 0.012 0 R2= 0.987 煤岩 压汞法（孔径＞36 nm） y = 32.35 x -0.227 0 R2= 0.985 煤岩 压汞法（孔径＜36 nm） y = 5.02 x -0.080 0 R2= 0.381 页岩 吸附法 y = 1 167.40 x + 0.000 5 R2= 0.405

下载CSV 表 3 砂岩、煤岩、页岩样品的渗透率校正方程 Table 3 Permeability modification equation of sandstone, coal and shale samples

图 6

Fig. 6

下载eps/tif图 图 6 NMR测试砂岩样品的Vc与T2谱之间关系[14] Fig. 6 Relationship between Vc and T2 of the sandstone samples by NMR tests

图 7

Fig. 7

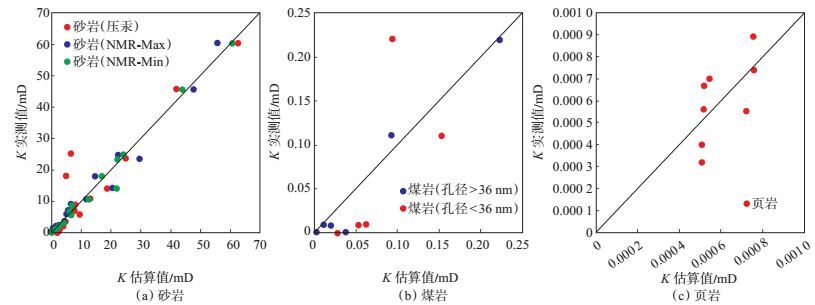
下载eps/tif图 图 7 利用分形理论模型估算岩石渗透率 Fig. 7 Rock permeability predicted by fractal theory model

从岩石渗透率预测结果来看，砂岩样品的预测效果最好[图 7（a）]，即利用NMR数据预测效果要略好于压汞数据。在煤岩样品中，孔径大于36 nm（主要为渗流孔）数据段的预测效果最好，而孔径小于36 nm（主要为吸附孔）数据段的预测效果相对较差[图 7（b）]，这表明，利用分形模型预测煤岩渗透率是有效的。页岩样品的渗透率预测效果比砂岩和煤岩差[图 7（c）]，这与页岩曾经历的强压实及复杂成岩演化有关^[31]，表明页岩渗透率极低（nD级），岩石的孔隙结构极为复杂，同时等效毛管迂曲度较大。

（1）压汞、NMR及N₂吸附实验分形计算结果表明，砂岩、煤岩及页岩的D_f主要为2.6~3.0，D_T主要为1.1~2.3，分形维数大小与岩石渗透率具有负相关性。

（2）煤岩的D_T值较小，表明煤岩的毛管迂曲度较小；D_f值较大，表明煤岩的微观孔隙结构及内部矿物排列方式极为复杂，这是造成渗透率降低的重要原因。页岩的D_f值较小，表明纳米级孔隙的分布规律较规则；D_T值较大，表明毛管迂曲度较大，流体渗流所需通过的路径较长，这是造成渗透率极低（nD级）的重要原因。砂岩受不同沉积、成岩演化的影响，岩石内部矿物组分差异较大，因而D_f值变化范围也较大。砂岩的D_T值大于煤岩而小于页岩，表明砂岩中毛管迂曲度大于煤岩，而小于页岩。

（3）影响岩石渗透率的因素包括：岩石的非均质性、孔喉分布、孔隙表面粗糙程度及毛管迂曲度等，其中毛管迂曲度对岩石渗透率的影响最大。建立了砂岩、煤岩、页岩样品的等效毛管迂曲度模型，煤岩的等效毛管迂曲度较小，砂岩中等，页岩较大。

（4）利用分形理论模型对39组岩石样品的渗透率进行预测，其中砂岩和煤岩的预测效果较好，但对于强非均质性页岩来说，渗透率已经达到nD级，虽然预测结果具有一定的符合度，但是预测精度仍有待进一步提高。