2. 中国石油集团科学技术研究院有限公司, 北京 100083
2. Research Institute of Science and Technology Co., Ltd., CNPC, Beijing 100083, China
乍得Bongor盆地花岗岩潜山储层裂缝发育,目前学界对其研究重点主要是岩性识别和流体性质识别方面[1-2],而对储层物性评价,尤其是渗透率定量计算方面的研究工作相对欠缺,这严重制约了该区基岩潜山油藏的开发。渗透率是油田开发所需的一个重要参数,但其影响因素多、建模难度大,至今没有形成统一的理论计算模型,尤其是对于含有裂缝的双重孔隙介质的渗透率计算模型研究尚不成熟[3]。在实际应用中,一般采用间接方法将可以直接测量的岩石物理参数转换为渗透率。例如,利用常规测井和成像测井资料,建立渗透率与裂缝孔隙度、裂缝开度及裂缝密度等参数的关系[4-5];基于阵列声波资料,利用斯通利波能量衰减计算双重介质渗透率[6]等。这些方法解释参数多、人工干预程度大,因此计算结果精度不高。渗透率预测具有影响因素多、规律模糊、难以准确全面描述的特点,机器学习是解决此类问题的一种有效途径。目前,机器学习已在储层评价中展现出巨大的应用潜力[7-9],如有监督学习、无监督学习和半监督学习等方法在复杂岩性/岩相识别[10-11]、曲线重构、物性参数计算等方面都取得了良好的应用效果。然而,在裂缝型储层中,裂缝的延伸尺度比孔隙大,难以通过岩心分析获得能充分表征地层渗流特征的岩石物理参数,这直接导致缺乏机器学习所需的标签数据。因此,无法直接使用上述机器学习方法对裂缝型储层进行评价。与岩心分析相比,试油过程能反映压力波及范围内(包含裂缝)所有储层特征对渗透率的影响,这就提供了解决机器学习应用问题的另外一种可能性,即将试油资料转换为标签数据。
针对乍得Bongor盆地花岗岩潜山裂缝型油藏,提出一种机理模型与机器学习数据驱动相融合的储层有效渗透率计算方法,将试油资料转换为机器学习所需的标签数据,挑选出有效的试油井段,并建立样本库,以期为该区裂缝型储层有效渗透率计算探索新的途径,指导油藏开发。
1 地质概况Bongor盆地位于乍得西南部、中非剪切带中段北侧,是受中非剪切带影响发育起来的中生代—新生代陆内拉分盆地。盆地在早白垩世经历了强烈的断陷,具有典型的被动裂谷特征,晚白垩世强烈抬升反转,古近纪统一成盆。盆地内沉积的中生界—新生界陆相碎屑岩地层厚度超过10 km,其中下白垩统泥岩是基岩潜山的油源和良好的区域盖层。Bongor盆地花岗质基岩潜山(下文简称潜山)[12]主要分布在盆地的北部斜坡区(图 1),其形成主要受构造背景和断裂活动的影响,类型以单面山为主,控山断层一般较陡,断面倾角大于50°。潜山在裂谷作用早期才翘倾形成的,其圈闭的幅度、规模和平面展布特征受断层控制。基岩是由岩浆岩和正变质岩构成的杂岩体,其中岩浆岩主要由花岗岩、正长岩和二长岩组成,变质岩主要为片麻岩和混合花岗岩,基岩形成或变质的时代为寒武纪纽芬兰世—新元古代。
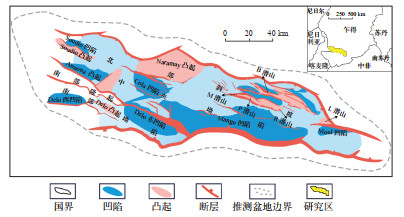
|
下载原图 图 1 Bongor盆地构造单元划分和潜山油田分布(据文献[12]和[13]修改) Fig. 1 Division of tectonic units and distribution of buried-hill oil fields in Bongor Basin |
潜山储层主要有风化壳孔隙型储层和内幕裂缝型储层两大类,储集空间主要包括破碎粒间孔、构造裂缝、构造-溶解缝、解理缝及溶孔等。储层纵向上具有明显的分带性,分为4个区带:风化壳、碎裂带、半充填裂缝碎裂带和致密带,其中,风化壳和碎裂带储集条件较好,向下进入潜山内部逐步变差。孔隙型储层主要发育在顶部风化壳,以破碎的粒间孔和溶蚀孔洞为主,向下过渡到以裂缝为主,局部沿裂缝发育溶蚀孔洞;裂缝型储层以构造活动形成的大量构造缝和解理缝为主,沿裂缝周围偶见裂缝的扩溶现象,发育溶蚀孔洞,裂缝和孔隙中常充填有绢云母、高岭石、绿泥石、伊蒙混层黏土以及次生石英等。潜山储层平面上分布广泛,但非均质性强,不同构造部位储层厚度和品质差异较大[13]。基岩储层发育主要受古构造位置、基岩岩性以及构造活动的影响,有利储层一般发育在局部构造高部位和主要断裂带附近。富含长英质矿物的基岩层段裂缝相对发育,沿裂缝风化淋滤作用强烈。频繁的构造活动在基岩中形成了多期构造裂缝,主断层附近裂缝更为发育。
2 有效渗透率计算方法原理与流程由于Bongor盆地花岗质基岩潜山岩性和储集空间复杂,加上储层纵向和横向非均质性均较强,测井响应特征也复杂多变,几乎是“一井一特征”,这大幅增加了测井资料解释的难度,例如裂缝充填程度和地层矿物变化增加了分析电性曲线响应特征的复杂度。以X-10井为例(图 2),取心段为花岗斑岩,黑云母和其他暗色矿物局部富集,裂缝极为发育,但大部分被绿泥石等矿物充填,单从电成像图像上难以将张开缝与充填缝区分开来。多种原因导致研究区潜山油藏发现初期测井解释与试油结果之间的矛盾一度非常突出,因此,划分裂缝类型、准确计算渗透率,进而评价储层有效性,成为提高潜山油藏解释符合率面临的主要难题。
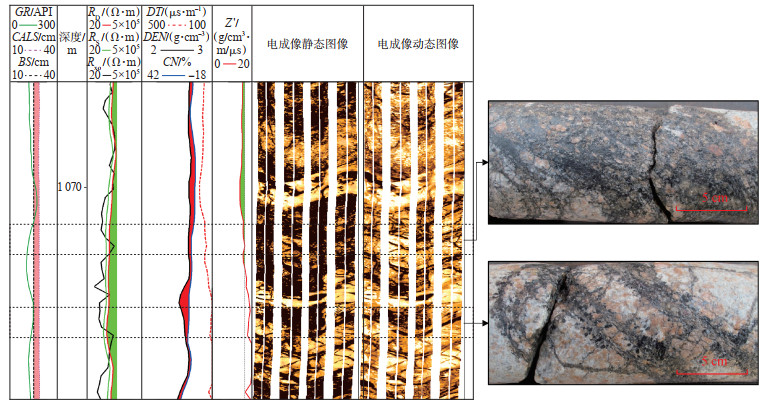
|
下载原图 图 2 Bongor盆地X-10井取心段测井曲线和岩心照片 Fig. 2 Well logs and core photos of coring intervals of well X-10 in Bongor Basin |
渗透率计算问题一般通过有监督机器学习(Supervised Machine Learning)[14]来解决,而训练机器学习模型需要用到样本库(Sample Dataset),其由输入曲线和标签共同构成。其中,输入曲线或特征(Feature)是指与渗透率变化相关的测井数据,标签(Label)是指某深度点地层对应的准确渗透率数据。有监督机器学习的目标就是找到一个最优函数或模型,将输入曲线正确地映射到渗透率。
Bongor盆地潜山具有相对丰富的试油数据,而对于裂缝型储层,通过试油过程可以获取反映裂缝发育尺度下的渗流特性参数,这是通过岩心分析难以实现的。因此,可以通过试油数据导出标签数据,但是试油数据并不能直接用作标签数据,需要有一个处理和转换过程。
油藏流体向井流动的规律满足达西定律,根据达西定律和径向压力扩散方程,对于圆形地质中心的一口井,供给边缘压力不变时,满足如下公式(法定单位)[15]:
| $ K_{\mathrm{e}}=\frac{I_{\mathrm{P}}}{h} \frac{\mu B\left(\ln \frac{r_{\mathrm{e}}}{r_{\mathrm{w}}}-\frac{1}{2}\right)}{2 \pi}=\frac{I_{\mathrm{P}}}{h} T_{\mathrm{C}} $ | (1) |
| $ I_{\mathrm{P}}=\frac{q}{\left(\bar{p}-p_{\mathrm{wf}}\right)} $ | (2) |
式中:Ke为储层有效渗透率,m2(1 m2 = 1.013 25× 1015 mD);IP为生产指数,m3/s/Pa(生产中常用单位为bbl/d/psi);h为储层有效厚度,m;B为流体体积系数;μ为流体黏度,Pa·s;re为泄油边缘半径,m;rw为井眼半径,m;q为产量,m3/s;p为地层平均压力,Pa;pwf为井筒流动压力,Pa;TC代表组合流体黏度、体积系数、供给半径、表皮系数等参数的试油条件。
对于同一试油井段,米生产指数(IP/h)与渗透率呈正比关系,地层系数K·h与IP也呈正比关系,下文中将称K·h或IP称为渗透率指示参数KIND。
定义由试井解释求取的有效渗透率为Ketest。从上述公式可以看出,当TC一致时,不用计算Ketest,而是直接依据KIND就可以比较TC一致时不同试油井段之间的渗透性差异。将这些具有渗透率可比性的井段放在一起就可以构建样本库,此规律是本文方法的根本依据。此外,试井解释模型需要较多的输入参数,其中就包含有效储层厚度,而在不知道渗透率的前提下很难准确给出潜山储层的有效厚度,这就形成了循环依赖,增加了计算Ketest的不确定性。KIND的计算相对容易,利用KIND直接比较TC一致井段的渗透性,将KIND作为样本库的标签数据依据,避开计算Ketest,这是本文方法的额外优势。
KIND为试油井段的单值标量参数,为了应用机器学习方法,必须将其转换为有效渗透率连续曲线Ke。转换方法为:选取某条渗透率敏感的测井曲线作为渗透率指示曲线KIND-Log,将其曲线值视为单值渗透率分配权重,将KIND逐点分配形成Ke连续曲线:
| $ {K_{{{\rm{e}}_i}}} = \frac{{{K_{{\rm{IND}}}}}}{{{R_{\rm{s}}}}}\frac{{\frac{{{K_{{\rm{IND }} - {{\log }_i}}} - {K_{{\rm{IND }} - {{\log }_{\min }}}}}}{{{K_{{\rm{IND }} - {{\log }_{\max }}}} - {K_{{\rm{IND }} - {{\log }_{\min }}}}}}}}{{\sum\limits_{{h_{{\rm{top }}}}} {^{{h_{{\rm{tottom }}}}}} \frac{{{K_{{\rm{IND }} - {{\log }_i}}} - {K_{{\rm{IND }} - {{\log }_{\min }}}}}}{{{K_{{\rm{IND }} - {{\log }_{\max }}}} - {K_{{\rm{IND }} - {{\log }_{{\rm{min }}}}}}}}}} $ | (3) |
式中:Kei为第i个深度点的有效渗透率,mD;KIND - Logi为第i个深度点的渗透率指示曲线值;KIND - Logmin和KIND - Logmax分别为试油井段渗透率指示曲线最小值和最大值;htop和hbottom分别为试油井段顶部和底部的深度,m;RS为深度采样间隔,m。
挑选TC一致的试油井段是关键步骤之一。采用建模条件一致性指示交会图(以下简称指示交会图),即
该方法融合了机理模型与机器学习数据驱动模型[16],关注点并不是机器学习算法本身,而是标签数据和样本库的构建过程。样本库构建方法也不是通过机理模型正演出训练样本[17],而是在岩石物理学、渗流力学等机理模型的指导下,依据现有研究成果和领域专家经验,通过上述建模数据一致化过程将学习样本挑选出来。完整的方法流程如图 3所示,共3个阶段:第一阶段是利用建模数据一致化过程形成Ke标签数据,其中另一个重要环节生成和挑选KIND - Log会在下节详细介绍。第二阶段是特征工程,目标是寻找渗透率敏感的输入曲线,与标签数据一起组成样本库。第一阶段和第二阶段的主要目标都是建立样本库,也是本文方法的主要关注点。第三阶段是利用样本库训练机器学习模型,然后在待评价井上进行有效渗透率预测,这一阶段是传统机器学习应用所关注的环节,涉及到了算法选择、模型参数优化和模型解释等主题。
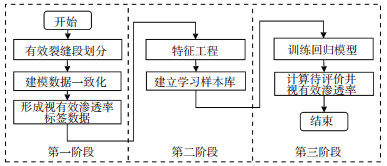
|
下载原图 图 3 机理模型与机器学习数据驱动相融合的储层有效渗透率计算方法流程框架 Fig. 3 Framework of effective permeability calculation method integrating mechanism model with machine learning data-driven techniques |
本次研究共收集了来自Bongor盆地B,L,M,P和R共5个潜山37口井的47层试油数据。潜山段一般为裸眼完井,试油方式为整段试油(油嘴128/64 in,1 in = 2.54 cm),试油段厚度为200~ 800 m。试油统计结果显示,生产指数为0.002~ 100.200 bbl/d/psi(0.04~2 311.90 m3/d/MPa)(1 bbl= 0.159 m3,1 psi=0.006 895 MPa),高产油层产量可达5 576.74 bbl/d(886.70 m3/d),而低产油层产量只有2.55 bbl/d(0.41 m3/d)(抽汲)。
3.2 有效裂缝发育段划分真正对试油产量有贡献的是有效裂缝,无效裂缝主要有三大类,即后期被充填或者关闭的张开裂缝、不连续或无延伸导致的无渗透性裂缝、钻井过程引发的各种诱导缝等。首先定性识别出完全无效裂缝,对应的无效储层段对产量没有贡献,其有效渗透率可视为零;其次,采用KIND - Log来刻画剩余储层。
挑选KIND - Log需要用到常规测井、电成像测井、阵列声波、录井、钻井、试油等多专业资料,并结合现有认识和专家经验,由人工进行分析,这是一个领域知识驱动的关键过程,属于传统测井解释范畴。
传统方法一般是通过由成像测井导出的裂缝密度、裂缝开度、倾角等参数,对裂缝型地层进行定量评价,但这些参数与常规测井等曲线存在纵向深度分辨率不匹配的问题。本文方法不直接使用这些参数构建样本库,而是在假定因裂缝发育引发的渗透性改变程度在探测范围为井筒周围的测井曲线上具有反映这一认识的基础上,将KIND - Log和输入曲线的选择范围扩展到常规测井、录井、钻井等曲线中,这在很大程度上丰富了选择范围,而KIND - Log的选择是否合理则由建模数据一致化过程来保证。
经过研究发现,乍得Bongor盆地潜山对裂缝发育敏感的曲线有:自然伽马(GR)、中子(CN)、密度(DEN)、声波时差(DT)、电阻率(RD)、致密段和裂缝段电阻率比值(RFR)、常规测井计算孔隙度(φ)(曲线名记为POR)、测井视波阻抗Z'(曲线名记为Z_APP)、微电阻率扫描成像动态和静态图像(FMI_DYN,FMI_STAT)、微电阻率扫描成像次生孔隙度(VISO)、斯通利波反射系数(STRC)、录井全烃(TG)、钻速(ROP)、井温导数(TEMP_D)等,这些曲线也称为KIND - Log候选曲线。此外,测井解释可获得六大类“优势岩性”序列:混合花岗岩、酸性岩、混合片麻岩、中性岩、片麻岩、基性岩(代码分别为MGRANITE,ACID,MGNEISS,INTERM,GNEISS,BASIC),优势岩性浅色矿物含量高、脆性高、塑性弱,同等构造应力条件下容易发育裂缝。
参照试油结果,总结得到有效裂缝发育段的特征:岩性为优势岩性、电成像图像上可见裂缝发育、φ≥ 4%,Z'≤ 15.5 g/cm3·m/μs,RD≤ 2 000 Ω·m,RFR ≥ 10,VISO >2%,STRC > 0.1,ROP明显变大、T'出现正异常等。根据这些特征,可以将每个试油井段的有效储层段划分出来。
3.3 建模数据一致化
建模数据一致化的目标是挑选有效建模井段和确定KIND - Log,这是一个反复迭代过程,步骤如下:①从KIND - Log候选曲线中选择出第i次迭代渗透率指示曲线KIND - Log(i);②对每个试油井段计算
最终有效建模井段将是有效裂缝发育段划分准确、KIND - Log选择合理、TC条件一致的试油井段,生成的标签数据Ke具有可比性。
经过对比,本文选择测井视波阻抗Z' 和孔隙度φ作为主要的KIND - Log曲线,其中,Z' 计算公式为
| $ Z^{\prime}=\frac{D E N}{D T} $ | (4) |
式中:Z' 为视波阻抗,g/cm3·m/μs;DEN为密度测井值,g/cm3;DT为声波时差测井值,μs/m。
Z' 是储层物性好坏的直接反映,与φ相比,Z' 计算较为简单直接,人工干预较少,指示交会图中数据点分布更为集中。
指示交会图分析结果如图 4所示,采用φ和Z'作为渗透率指示曲线的有效建模井段分别有12个和14个,总共筛选出19口井26个有效建模井段。
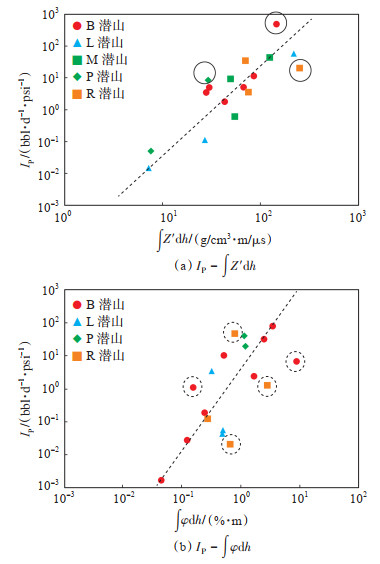
|
下载原图 图 4 建模条件一致性指示交会图 Fig. 4 Crossplot of modeling consistency indication |
图 4中圆形虚线标注的为无效数据点,对应的是非有效建模井段,被排除的主要原因包括:①井眼扩径严重,测井曲线尤其是孔隙度曲线失真严重;②数据的来源井为潜山兼探井,潜山段钻井进尺较短;③试井解释采用径向复合模型,井筒周围测井曲线特征与压力波及范围内地层动态渗流特征不完全一致;④纵向岩性变化快,难以准确建立KIND - Log曲线;⑤油质发生变化,与主趋势线TC不一致;⑥是低产井段,IP计算误差较大。
研究中并不追求将所有试油井段都纳入样本库,而是在覆盖了潜山不同部位、不同岩性、不同品质储层的前提下,只挑选数据质量高的井段。最终TC取流体黏度为2.55~5.25 mPa·s、体积系数为1.02~1.16、表皮系数为1.01~5.09、供给半径约为500 m,试井解释模型为双孔或双渗模型。
从建模有效井段中选择结果可靠的6层,重新进行试井解释,求取K·h,然后回归得到IP与K·h的转换公式,据此生成样本库的标签数据Ke:
| $ K \cdot h=2574.9 I_{\mathrm{P}}^{0.9712} $ | (5) |
式中:K · h为地层系数,mD·m;IP为生产指数,bbl/d/psi。
3.4 特征工程特征工程是指挑选或构建输入测井曲线的过程,其结果对最终模型的预测性能具有较大影响[18-19]。考虑到潜山测井资料采集情况,输入曲线以常规测井曲线为主,但是仅仅使用原始测井曲线是不够的,还需要构建新的特征曲线,增加输入曲线信息的丰富程度。特征构建方法一般以领域知识和机理模型驱动为主,无监督学习为辅,从以下3个方面构建新特征。
(1)岩性敏感测井曲线。潜山岩石大致由浅色矿物系列和暗色矿物系列造岩矿物组成,两者在中子、密度和自然伽马曲线上的响应特征不同,同时由于后期变质作用和变质程度的影响,变质岩比岩浆岩具有更强的非均质性,变质岩测井曲线呈锯齿状,而岩浆岩测井曲线则呈平直状,自然伽马曲线尤为明显。据此导出5条新的岩性特征曲线:自然伽马窗口标准差(GR_WSDEV)和窗口均值(GR_WAVG),视中子-密度孔隙度差(CDPD)、窗口标准差(CDPD_WSDEV)和窗口均值(CDPD_WAVG),深度窗长取3 m,CDPD定义如下:
| $ C D P D=\left(\frac{D E N_{\max }-D E N}{D E N_{\max }-D E N_{\min }}-\frac{C N-C N_{\min }}{C N_{\max }-C N_{\min }}\right) \times 100 \% $ | (6) |
式中:CDPD为视中子-密度孔隙度差,%;DEN为密度曲线值,g/cm3;DENmin为视流体密度,g/cm3,取2 g/cm3;DENmax为视骨架密度,g/cm3,取3 g/cm3;CN为中子曲线值,%;CNmin为视骨架中子孔隙度,%,取-18%;CNmax为视流体中子,%,取42%。视骨架密度和视骨架中子孔隙度均没有采用习惯取值,是为了加大两者之间的差异程度,以便更好地指示岩性差异。
(2)聚类-岩心标定相结合的方法得到测井岩性识别曲线。首先采用Geolog FacimageTM[20]模块中的MRGC(Multi-Resolution Graph-Based Clustering)算法[21],输入GR,GR_WSDEV,GR_WAVG,DEN,CN,DT,CDPD,CDPD_WSDEV和CDPD_WAVG共9条曲线,聚类得到16个岩性类别,曲线名为LITH_MRGC;然后根据岩心薄片鉴定结果对聚类结果进行标定,由于其中包含有混合花岗岩-酸性岩、片麻岩-中性岩、片麻岩-混合片麻岩等这些测井特征有所重叠的过渡岩性,因此聚类岩性类别要多于六大类。
(3)辅助表征潜山储层纵向分带特性的归一化垂深曲线TVDSSnorm,定义为
| $ { TVDSS }_{\text {norm }_i}=\frac{ { TVDSS }_i-{ Basement }_{\text {top }}}{ { Basement }_{\text {bottom }}- { Basement }_{\text {top }}} $ | (7) |
式中:TVDSSnormi为第i个深度点的归一化垂深;TVDSSi为第i个深度点的垂深,m;Basementtop和Basementbottom分别为整个潜山油藏的顶部垂深和底部垂深,m。
图 5为试油井段TVDSSnorm和IP的交会图,利用该交会图可以检查试油井段是否符合纵向分带变化规律,建模有效井段主要来自交会点在主趋势线上的试油井段。
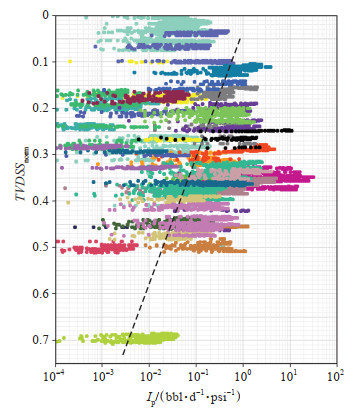
|
下载原图 图 5 归一化垂深与生产指数交会图(颜色代表不同井段) Fig. 5 Crossplot of TVDSSnorm and IP |
最终样本库由19口井的51 348个深度点数据组成,视有效渗透率为0.01~1 601.50 mD,其中85% 为非储层样本数据。特征曲线包含GR,GR_WSDEV,GR_WAVG,DEN,CN,DT,CDPD,CDPD_WSDEV,CDPD_WAVG,TVDSS_NORM,Z_APP,LITH_MRGC,RD(深电阻率),RS(浅电阻率)共14条;LITH_MRGC经过One-Hot编码得到16条岩性编码曲线,曲线名分别为LM_0,LM_1,…,LM_15。整个样本库具有足够的代表性,基本覆盖到了主要的潜山带,包含不同岩性、不同储层品质和不同试油产量井段的输入曲线响应特征。
4 回归建模与应用实例为了检验该方法的有效性,从样本库中挑选出X-5井作为检验井,该井的2 875个样本点数据不参与建模过程,剩余的样本点共48 473个数据点作为模型选择及最终模型训练的训练集。
4.1 回归建模由于渗透率为连续数值,所以使用监督机器学习中的回归算法来建模。上述过程形成的样本库属于典型的“扁平表格数据”(Tabular Data),这也是测井解释中经常碰到的一大类数据。已有研究表明,采用集成学习中的梯度提升决策树算法(Gradient Boosting Decision Tree,GBDT)处理“扁平表格数据”,比深度神经网络的性能表现更优异[22-24],其基本原理是利用梯度增强方法将多个弱回归树结果累加起来得到最终预测结果。
回归建模过程:①确定候选算法。k-最近邻(k-Nearest Neighbors,KNN)[25]、支持向量机(Support Vector Machine,SVM)[26],LightGBM[27],XGBoost[28]共4种回归算法,其中LightGBM和XGBoost均为GBDT算法的增强实现。②模型评估。因为强调高渗层的预测准确率,选择均方根对数误差RMSLE作为模型选择评估指标,采用10折交叉检验(Cross Validation,CV)作为模型评估方法,均方根误差RMSE作为检验集准确率评估指标。③超参数优化。梯度提升树算法具有很多参数,但实际使用时并不需要对每个参数进行调整[29],使用贝叶斯超参数优化[30](Bayesian Optimization)方法获得最优模型参数。④编程实现。利用Python编程实现整个建模和计算过程,其中用到了scikit-learn[31]和scikit-optimize[32]开源代码库。
从模型评估结果(表 1)可以看出,XGBoost算法无论是在训练集还是检验集均表现最好。同时,研究中也使用了FLAML[33]库进行了自动模型选择,结果显示XGBoost算法仍然最优。由于KNN算法计算过程直观、易于理解,而且性能也满足要求,因此选择XGBoost + KNN作为双重预测模型参与视有效渗透率计算。
|
|
下载CSV 表 1 不同算法回归建模评估结果 Table 1 Results of regression modeling and evaluation by different algorithms |
利用上述模型预测得到的视有效渗透率为Kepred,可用于有效储层段划分和辅助进行裂缝类型解释。经过研究得到储层有效性评价标准:Ke ≥ 1 mD为有效储层、Ke≥ 50 mD为好储层。
根据X-5检验井的解释成果(图 6),该井潜山段纵向岩性复杂多变,从电成像图像上可以看到以破碎结构为主,裂缝较为发育;从Kepred可看出,有效储层段位于潜山顶部的混合花岗岩和混合片麻岩段,裂缝以张开缝为主;下段有效渗透率很小,以充填程度较高的裂缝为主,为无效储层。Kepred响应特征与试油结果一致,该井上段试油产油量为154.84 bbl/d(油嘴124/64 in),下段试油抽汲结果为干层。
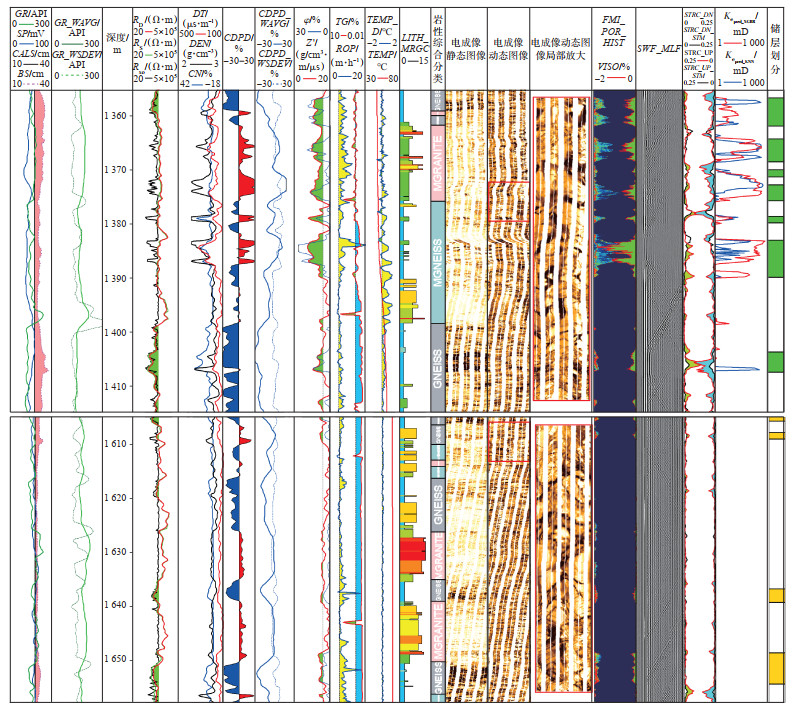
|
下载原图 图 6 Bongor盆地X-5井有效渗透率计算综合成果 注:GR_WAVG.自然伽马窗口均值;GR_WSDEV.自然伽马窗口标准差;CDPD_WAVG.视中子-密度孔隙度窗口均值;CDPD_WSDEV.视中子-密度孔隙度窗口标准差;TEMP.井温;TEMP_D.井温导数;LITH_MRGC.岩性聚类;FMI_POR_HIST.电成像孔隙度谱;VISO.大孔占比;SWF_MLF. 全波列变密度图像;STRC_DN.下行波反射系数;STRC_UP.上行波反射系数;Kepred_XGBR.XGBoost有效渗透率;Kepred_KNN.KNN有效率渗透率。 Fig. 6 Results of effective permeability calculation of well X-5 in Bongor Basin |
对于测井解释来说,仅仅计算出有效渗透率数值是不够的,还需要获得模型的预测细节。因此使用SHAP[34-35]值对XGBoost这种黑箱模型的预测过程进行解释。SHAP采用合作博弈论方法计算样本特征对模型预测输出的影响程度,X-5井XGBoost和KNN模型的SHAP Beeswarm图如图 7所示,图中列出了前10个重要的输入曲线排序以及曲线值大小对于Ke计算结果高低的影响,SHAP值为正表明增大Ke,为负表明减小Ke。
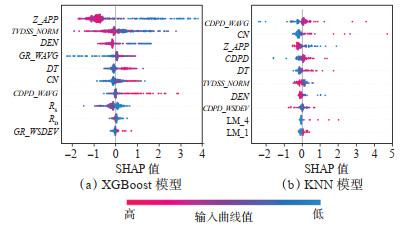
|
下载原图 图 7 Bongor盆地X-5井SHAP Beeswarm图 Fig. 7 SHAP Beeswarm plot of well X-5 in Bongor Basin |
对于XGBoost模型来说,对视有效渗透率预测影响程度排名前10的曲线是Z_APP,TVDSS_NORM,DEN,GR_WAVG,DT,CN,CDPD_WAVG,RS,RD和GR_WSDEV。对各曲线分析如下:①Z_APP。裂缝发育程度和溶蚀强度在井周处的综合反映,也是样本库的KIND-Log(final)曲线,与有效渗透率相关性最强。②TVDSS_NORM。潜山储层纵向分带性体现,储层埋藏越深,则渗透性越差。③DEN,GR_WAVG,DT,CN,CDPD_WAVG等,综合反映岩性影响。④RS,RD。潜山有效储层的基本特征是高阻背景下的低阻段,岩性相同时,电阻率下降幅度越大,指示储层渗透性越好、裂缝充填程度越低,是岩性、渗透率和物性影响的综合体现。XGBoost模型充分利用了这些最主要的输入曲线信息,与潜山储层品质控制因素定性认识一致,说明模型预测是可靠的,也获得了较高的预测精度。相比之下,KNN模型主要利用了岩性、物性和储层纵向分带性等曲线进行预测,其计算精度不如XGBoost模型。
由于测井岩性识别曲线LITH_MRGC为类别型数据,经过One-Hot编码后作为特征曲线,SHAP对此类曲线分析能力有限,为此建立一个不包含LITH_MRGC的模型XGBoost2。从表 1可看出,包含LITH_MRGC的XGBoost1的预测准确率更高,因此添加岩性聚类结果可以改善预测效果。
5 结论(1)在裂缝型储层渗透率计算中应用有监督机器学习的难点并不在于算法本身,而在于获取能反映裂缝发育尺度渗流特征的标签数据,但其通过岩心资料获取难度很大,利用试油数据转换是另一种可行途径。
(2)将试油数据转换为机器学习所需的标签数据的关键技术是利用建模条件一致性指示交会图执行建模数据一致化过程,挑选出有效的试油井段,并建立样本库。标签为TC一致时的视有效渗透率,输入曲线为反映潜山岩性、裂缝发育程度、储层纵向分带性等特征的原始或导出测井曲线。
(3)在机理模型与机器学习数据驱动相融合的储层有效渗透率计算方法回归建模中,XGBoost模型计算的检验井视有效渗透率结果与试油结果一致,计算结果准确可靠。
(4)本文方法拓展了机器学习方法在测井解释中的应用范围,虽然计算得到的是视有效渗透率,与真实有效渗透率有差异,但具有相对比较意义和实用价值,可用于划分裂缝类型、评价储层有效性等。
| [1] |
王楠. 乍得Bongor盆地潜山岩性识别及储层测井综合评价. 科学技术与工程, 2019, 19(27): 66-73. WANG Nan. Lithology identification and well-logging comprehensive evaluation of basement reservoir in Bongor Basin, Chad. Science Technology and Engineering, 2019, 19(27): 66-73. |
| [2] |
汪文湛, 文光耀, 程维营, 等. Bongor盆地花岗岩潜山流体性质识别. 石化技术, 2019, 26(6): 138-141. WANG Wenzhan, WEN Guangyao, CHENG Weiying, et al. Identification of granitic buried-hill reservoir fluid properties in Bongor Basin. Petrochemical Industry Technology, 2019, 26(6): 138-141. |
| [3] |
孙建孟, 闫国亮. 渗透率模型研究进展. 测井技术, 2012, 36(4): 329-335. SUN Jianmeng, YAN Guoliang. Review on absolute permeability model. Well Logging Technology, 2012, 36(4): 329-335. |
| [4] |
任杰. 碳酸盐岩裂缝性储层常规测井评价方法. 岩性油气藏, 2020, 32(6): 129-137. REN Jie. Conventional logging evaluation method for carbonate fractured reservoir. Lithologic Reservoirs, 2020, 32(6): 129-137. |
| [5] |
吴伟, 邵广辉, 桂鹏飞, 等. 基于电成像资料的裂缝有效性评价和储集层品质分类: 以鸭儿峡油田白垩系为例. 岩性油气藏, 2019, 31(6): 102-108. WU Wei, SHAO Guanghui, GUI Pengfei, et al. Fracture effectiveness evaluation and reservoir quality classification based on electrical imaging data: A case study of Cretaceous in Ya'erxia Oilfield. Lithologic Reservoirs, 2019, 31(6): 102-108. |
| [6] |
严伟, 张冲, 胡挺, 等. 利用斯通利波估算火成岩地层渗透率. 岩性油气藏, 2013, 25(1): 107-110. YAN Wei, ZHANG Chong, HU Ting, et al. Calculation of permeability in igneous rock formation based on Stoneley wave. Lithologic Reservoirs, 2013, 25(1): 107-110. |
| [7] |
李宁, 徐彬森, 武宏亮, 等. 人工智能在测井地层评价中的应用现状及前景. 石油学报, 2021, 42(4): 508-522. LI Ning, XU Binsen, WU Hongliang, et al. Application status and prospects of artificial intelligence in well logging and formation evaluation. Acta Petrolei Sinica, 2021, 42(4): 508-522. |
| [8] |
匡立春, 刘合, 任义丽, 等. 人工智能在石油勘探开发领域的应用现状与发展趋势. 石油勘探与开发, 2021, 48(1): 1-11. KUANG Lichun, LIU He, REN Yili, et al. Application and development trend of artificial intelligence in petroleum exploration and development. Petroleum Exploration and Development, 2021, 48(1): 1-11. |
| [9] |
王华, 张雨顺. 测井资料人工智能处理解释的现状及展望. 测井技术, 2021, 45(4): 345-356. WANG Hua, ZHANG Yushun. Research status and prospect of artificial intelligence in logging data processing and interpretation. Well Logging Technology, 2021, 45(4): 345-356. |
| [10] |
孙予舒, 黄芸, 梁婷, 等. 基于XGBoost算法的复杂碳酸盐岩岩性测井识别. 岩性油气藏, 2020, 32(4): 98-106. SUN Yushu, HUANG Yun, LIANG Ting, et al. Identification of complex carbonate lithology by logging based on XGBoost algorithm. Lithologic Reservoirs, 2020, 32(4): 98-106. |
| [11] |
武中原, 张欣, 张春雷, 等. 基于LSTM循环神经网络的岩性识别方法. 岩性油气藏, 2021, 33(3): 120-128. WU Zhongyuan, ZHANG Xin, ZHANG Chunlei, et al. Lithology identification based on LTSM recurrent neural network. Lithologic Reservoirs, 2021, 33(3): 120-128. |
| [12] |
窦立荣, 魏小东, 王景春, 等. 乍得Bongor盆地花岗质基岩潜山储层特征. 石油学报, 2015, 36(8): 897-904. DOU Lirong, WEI Xiaodong, WANG Jingchun, et al. Characteristics of granitic basement rock buried hill reservoir in Bongor Basin, Chad. Acta Petrolei Sinica, 2015, 36(8): 897-904. |
| [13] |
余朝华, 杜业波, 肖坤叶, 等. 乍得Bongor盆地基岩潜山储层特征与影响因素研究. 岩石学报, 2019, 35(4): 1279-1290. YU Zhaohua, DU Yebo, XIAO Kunye, et al. Characteristics and influence factors of basement buried-hill reservoir in Bongor Basin, Chad. Acta Petrologica Sinica, 2019, 35(4): 1279-1290. |
| [14] |
SINGH A, THAKUR N, SHARMA A. A review of supervised machine learning algorithms[R]. New Delhi, India: 2016 The3rd International Conference on Computing for Sustainable Global Development(INDIACom), 2016.
|
| [15] |
刘能强. 实用现代试井解释方法. 5版. 北京: 石油工业出版社, 2008: 29-31. LIU Nengqiang. The utility of modern well test interpretation method. 5th ed. Beijing: Petroleum Industry Press, 2008: 29-31. |
| [16] |
肖立志. 机器学习数据驱动与机理模型融合及可解释性问题. 石油物探, 2022, 61(2): 205-212. XIAO Lizhi. The fusion of data-driven machine learning with mechanism models and interpretability issues. Geophysical Prospecting for Petroleum, 2022, 61(2): 205-212. |
| [17] |
LIANG Lin, LEI Ting. Machine learning-enabled automatic sonic shear processing. Petrophysics, 2021, 62(3): 282-295. |
| [18] |
LI Hongqi, GUO Haifeng, GUO Haimin, et al. Data mining techniques for complex formation evaluation in petroleum exploration and production: A comparison of feature selection and classification methods[R]. Wuhan, China: 2008 IEEE PacificAsia Workshop on Computational Intelligence and Industrial Application, 2008.
|
| [19] |
ZHENG A, CASARI A. Feature engineering for machine learning: Principles and techniques for data scientists. Sebastopol, California: O'Reilly Media, Inc., 2018.
|
| [20] |
Aspen Tech. Aspen Geolog[EB/OL]. [2023-07-20]. https://www.aspentech.com/en/products/sse/aspen-geolog.
|
| [21] |
YE Shinju, RABILLER P. A new tool for electro-facies analysis: Multi-resolution graph-based clustering[R]. Dallas, Texas, USA: SPWLA 41st Annual Logging Symposium, 2000.
|
| [22] |
GRINSZTAJN L, OYALLON E, VAROQUAUX G. Why do tree-based models still outperform deep learning on tabular data?[DB/OL]. (2022-07-18)[2023-07-20]. https://arxiv.org/abs/2207.08815.
|
| [23] |
SHWARTZ-ZIV R, ARMON A. Tabular data: Deep learning is not all you need. Information Fusion, 2022, 81: 84-90. |
| [24] |
GORISHNIY Y, RUBACHEV I, KHRULKOV V, et al. Revisiting deep learning models for tabular data[DB/OL]. (2021-11-10)[2023-07-20]. https://arxiv.org/abs/2106.11959.
|
| [25] |
FIX E, HODGES J L. Discriminatory analysis—Nonparametric discrimination: Consistency properties. International Statistical Review/Revue Internationale de Statistique, 1989, 57(3): 238-247. |
| [26] |
CORTES C, VAPNIK V. Support-vector networks. Machine Learning, 1995, 20(3): 273-297. |
| [27] |
KE Guolin, MENG Qi, FINLEY T, et al. LightGBM: A highly efficient gradient boosting decision tree[M]//GUYON I, VON L U, BENGIO S, et al. 31st Advances in neural information processing systems 30(NIPS 2017). Massachusetts, USA: MIT Press, 2017.
|
| [28] |
CHEN Tianqi, GUESTRIN C. XGBoost: A scalable tree boosting system[C]//KRISHNAPURAM B, SHAH M, SMOLA A, et al. Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining. New York: Association for Computing Machinery, 2016.
|
| [29] |
Microsoft Corporation. Parameters tuning—Light GBM 4.0.0.99documentation. html[EB/OL]. [2023-07-20]. https://lightgbm.readthedocs.io/en/latest/Parameters-Tuning.html.
|
| [30] |
SNOEK J, LAROCHELLE H, ADAMS R P. Practical bayesian optimization of machine learning algorithms[DB/OL]. (2012-08-29)[2023-07-20]. https://arxiv.org/abs/1206.2944.
|
| [31] |
PEDREGOSA F, VAROQUAUX G, GRAMFORT A, et al. Scikit-Learn: Machine learning in python. Journal of Machine Learning Research, 2011, 12(85): 2825-2830. |
| [32] |
HEAD T, KUMAR M, NAHRSTAEDT H, et al. Scikit-optimize/scikit-optimize[DB/OL]. (2022-04-12)[2023-07-20]. https://zenodo.org/record/6451894.
|
| [33] |
WANG Chi, WU Qingyun, WEIMER M, et al. FLAML: A fast and lightweight Auto ML library[DB/OL]. (2021-05-19)[2023-07-20]. https://arxiv.org/abs/1911.04706.
|
| [34] |
LUNDBERG S M, LEE S I. A unified approach to interpreting model predictions[C]//Advances in Neural Information Processing Systems 30(NIPS 2017). Long Beach, California, USA: Neural Information Processing Systems Foundation, Inc. (NeurIPS), 2018.
|
| [35] |
LUNDBERG S M, ERION G, CHEN H, et al. From local explanations to global understanding with explainable AI for trees. Nature Machine Intelligence, 2020, 2(1): 56-67. |
 2023, Vol. 35
2023, Vol. 35



