2. 中国石油勘探开发研究院 西北分院, 兰州 730020;
3. 中国石油超深层复杂油气藏勘探开发技术研发中心, 新疆 库尔勒 841000;
4. 中国石油大学(华东)地球科学与技术学院, 山东 青岛 257061
2. PetroChina Research Institute of Petroleum Exploration & Development-Northwest, Lanzhou 730020, China;
3. Research and Development Center for Exploration and Development Technology of Ultra Deep Complex Oil and Gas Reservoirs, CNPC, Korla 841000, Xinjiang, China;
4. School of Geosciences, China University of Petroleum(East China), Qingdao 257061, Shandong, China
提高地震数据分辨率是一项系统工程,涉及采集、处理和解释三大环节。近年来,虽然地震数据采集技术与工程设计方法快速发展,但由于受地震基础理论和硬件发展限制,很难在采集阶段进一步减少地震数据的能量损失。利用地震资料解释中的分频、交汇等技术,虽然能够检测出与岩性相关的衰减信号,但其严重依赖地震资料所保留的岩性相应信息。因此,地震资料的处理质量对提高数据分辨率和解决地质问题意义重大。
沙漠近地表地层多为疏松沙砾,其对地震波能量的吸收衰减严重,导致地震波在穿过表层后出现振幅衰减和相位畸变问题,因此沙漠工区资料多具有主频低、频带窄的特点。如何有效且保真地提高资料主频、拓宽资料频带、恢复衰减信号一直是地震资料处理人员亟待解决的难题[1-3]。反褶积作为诸多提高分辨率方法中最常用的方法之一,已经得到了快速发展,其中根据不同的地震子波估计方法,已经发展出了谱模拟反褶积和预测反褶积等多种方法。由于实际地震资料复杂多变,对其子波的估计技术存在瓶颈,因此反褶积方法对于消除沙漠表层吸收衰减影响的能力有限。针对这一问题,众多学者提出了假设条件简单、结果稳定的品质因子Q补偿方法,如Wang[4]提出的稳定补偿方法,在一定程度上解决了高频补偿过量的问题,但在面对双复杂地区资料时,其假设条件难以保证补偿结果的保真性。因此,为了提高假设的准确性,更多学者开始从地层品质因子Q入手,通过对估算Q和反Q滤波稳定补偿算法的研究,从地质属性的角度来解决补偿假象的问题。从此,Q值的估算方法得到了快速发展,如王晓涛等[5]认为Q是决定能量衰减程度与速度的关键因素,因此从反射波的传播衰减规律角度估算Q值;蒋立等[6]验证了地表一致性反褶积方法与近地表Q补偿方法的适用条件及稳定性,证明戈壁区适合采用地表一致性反褶积方法,沙漠区适合采用近地表Q补偿方法;宋吉杰等[7]结合检波点的实测Q值和折射波法估算的相对Q值构建了高精度Q场,提出了基于Q值融合估算方法,进一步促进了Q值的准确估算;李伟娜等[8]提出了一种基于双线性回归的Q估算法,通过模型与实际资料的测试和应用,获得了与近地表模型分层一致且地质意义明确的估计Q场。以上Q值估算方法虽在一定程度上提高了估计精度,但并没有对Q值估算的真实性进行研究,针对这一问题,利用双测井约束估算Q值,可为结果的保真性提供重要依据。
压缩感知作为一种新型采样理论,现已在数学科学、医学成像和天文成像中取得重要应用成果。国内外研究人员对这一理论进行了大量的研究,并将其应用于地震勘探领域。韩立国等[9]利用压缩感知理论,在频率域将扩展频率数据的低频能量替换原始数据等范围内的低频能量,得到拓频后的频率域信息,再进行反傅里叶变换进而得到低频补偿数据;张莹[10]将扩展频率数据的低频和高频能量与原始数据的主频能量相结合,形成了最终的全频补偿地震数据;Sun等[11]利用信息约束来加强低频补偿对噪声的可靠性,但该方法仅限于低频。以上3种主要方法在拓展低频和高频方面均取得了良好的效果,但压缩感知理论作为数学算法,其拓频方法为数据驱动,并没有对保真性进行保护。针对这一问题,利用井约束建立基于压缩感知的拓频基函数,在保证数据驱动算法优势的同时,也利用井数据保护了其准确性。
针对沙漠区提出一种基于Q补偿、Q层析建模成像和压缩感知的联合高保真、高分辨率处理(双高处理)方法,首先利用约束估计的相对Q场对叠前记录进行稳定Q补偿,再对补偿后的数据进行Q层析建模成像来增加成像的纵向分辨率,最后利用压缩感知拓频方法重建反射系数,进行叠后补偿处理,并将该方法在尼日尔Agedem地区进行野外数据应用,以期为提高薄储层识别能力及提高油气勘探效率提供依据。
1 近地表Q叠前吸收补偿方法 1.1 近地表Q叠前吸收补偿方法理论针对地震波传播的吸收衰减,近地表Q补偿方法可消除疏松地表带来的影响。在整个联合高分辨率处理过程中,首先将Q补偿方法应用于叠前记录的高分辨率处理,其中如何估计准确的Q值是关键[12]。为使结果具有准确性,借助微测井测量来求取近地表的实测Q值,具体分为如下几个步骤。
(1)通过双井微测井测量数据求取近地表的实测Q值,其结果对整个工区Q值的准确求取起决定性作用[13]。利用双井微测井数据的直达波来进行Q值的求取,能很好地反映近地表低降速带对地震波能量和频率的影响。通过分析微测井数据井底检波器和地面检波器的频率属性和振幅属性,结合质心频移法和峰值频移法各自的优点,采用改进的峰值频移法,分析井底检波器峰值频率fm到地面检波点拾取主频f的移动,进而反演调查点的表层Q值,峰值频移法的计算公式为
| $ Q_{\text {实测 }}=\frac{\pi t f f_{\mathrm{m}}^2}{2\left(f_{\mathrm{m}}^2-f^2\right)} $ | (1) |
式中:Q实测为近地表实测Q值;fm为井底检波器峰值频率,Hz;f为地面检波点拾取主频,Hz;t为表层旅行时,s。
(2)计算表层旅行时t。根据拾取的折射波初至信息,利用层析反演等近地表速度反演方法,计算出工区的近地表速度、厚度、表层旅行时等信息。
(3)计算相对振幅衰减系数R。表层速度小或旅行时大,则表现为较强的吸收衰减,这种吸收衰减和地表具有一致性,为了体现这种相对差异的比例关系,定义R为相对振幅衰减系数。首先统计原始地震数据(折射波或反射波)每一道的振幅值,再在给定的时窗内计算每个地震道的均方根振幅值,最后分别统计炮点、检波点的振幅能量,计算出近地表因素对原始地震数据振幅的影响,求取期望补偿平均能量水平,进而得到相对振幅衰减系数R[14]。
(4)结合相对振幅衰减系数和表层旅行时,利用谱比法计算Q值:
| $ R F_{\text {scale }}=\frac{A(f)}{A_0(f)}=\mathrm{e}^{-\frac{\pi f t}{Q}} $ | (2) |
| $ Q_{\text {相对 }}=-\frac{\pi f t}{\ln \left(R F_{\text {scale }}\right)} $ | (3) |
式中:R为相对振幅衰减系数;Fscale为比例调节因子(目的是使RFscale < 1,从而计算出的Q> 0);A0(f) 为震源激发的地震波振幅;A(f) 为衰减之后的地震波振幅;Q相对为近地表相对Q值。
(5)实测Q值和相对Q值的标定。在同一位置点,将微测井计算的实测Q值作为约束条件,标定基于叠前地震数据求取的相对Q值,根据两者的差异,建立两者的比值关系M,即
| $ M=\frac{Q_{\text {实测 }}}{Q_{\text {相对 }}} $ | (4) |
根据标定M值的区间范围,进行Q值拟合处理。对于标定后的Q值与微测井计算的Q值线性误差太大的点,进行人工剔除,直至拟合后的Q值与微测井计算的Q值非常接近为止,最后得到全工区Q场。
得到工区估计Q场后,按如下方法对叠前地震记录进行补偿。
将一维波动方程进行傅里叶变换:
| $ \frac{\partial^2 U(z, \omega)}{\partial z^2}+k_z{ }^2 U(z, \omega)=0 $ | (5) |
式中:U(z,ω)为波函数的谱,其中z为波的传播距离,m;ω为角频率,Hz;kz为空间复波数。
考虑地震波吸收效应得到稳定的表层吸收补偿算法,可对叠前数据在频率域进行表层Q空变补偿:
| $ \begin{array}{c} U(\tau+\Delta \tau, \omega)=U(\tau, \omega) \cdot \\ \exp \left[\left(\frac{\omega}{\omega_{\mathrm{h}}}\right)^{-\gamma} \frac{\omega \Delta \tau}{2 Q}\right] \exp \left[i\left(\frac{\omega}{\omega_{\mathrm{h}}}\right)^{-\gamma} \omega \Delta \tau\right] \end{array} $ | (6) |
式中:U(τ + Δτ,ω) 表示经过振幅和相位补偿后的频率域地震数据,其中∆τ为表层旅行时增量;U(τ,ω)为未经补偿的频率域数据,其中τ为近地表旅行时,s;ωh为参考频率,Hz,是与地震波频带的最高频率有关的一个调整参数。
式(6)是由波动方程推导的补偿算式的基础,等式右侧由振幅补偿项和相位补偿项构成完整的Q补偿。Wang[4]提出了稳定的Q补偿算法,对振幅项做了如下改进:
| $ \varLambda(\omega)=\frac{\beta(\omega)+\rho^2}{\beta^2(\omega)+\rho^2} $ | (7) |
式中:Λ(ω) 为稳定的振幅补偿量;β(ω) 为原始振幅量;ρ2为稳定因子。
| $ \beta(\omega)=\exp \left[-\left(\frac{\omega}{\omega_{\mathrm{m}}}\right)^{-\frac{2}{\pi} \tan ^{-1}\left(\frac{1}{2 Q}\right)} \frac{\omega}{2 Q} \mathrm{t}\right] $ | (8) |
| $ \rho^2=\exp \left[-\left(0.23 G_{\lim }+1.63\right)\right] $ | (9) |
式中:Glim是增益限制,dB,是一个可调节参数;ωm为中心频率,Hz,与地震波频带的最高频率有关。
上述算法的稳定性体现在可以通过增益限制控制补偿的频带范围,防止高频噪音的过度补偿[16],同时还可调整相位,解决地层吸收造成的地震波能量损失和频散问题。
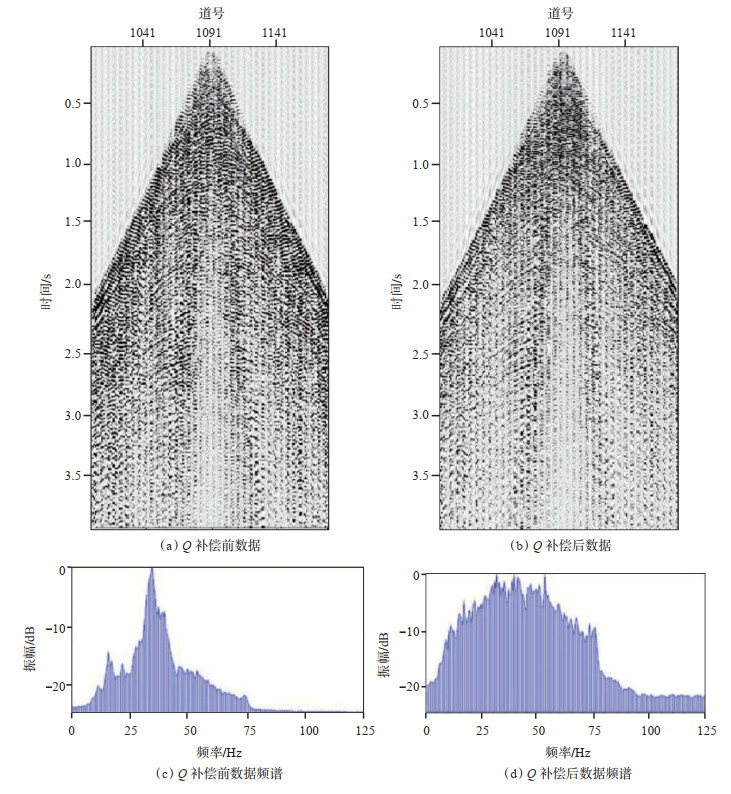
1.2 近地表Q叠前吸收补偿测试为验证近地表Q的叠前补偿效果,实验首先选取尼日尔Agedem地区叠前数据进行测试。从图 1的单炮记录展示中可以看出,处理后的数据具有更高的信噪比、分辨率和一致性,且同相轴更光滑连续,细小结构刻画得更为清晰。由于低降速带的影响,炮集频率较低,2~3 s处目的区域有效轴无法呈现,而处理后的数据有效信息能量增强,有效信息呈现更为清晰明显。从频谱中可以看出近地表Q补偿后数据频带更宽(频带宽度从35 Hz拓宽至约70 Hz),中—高频能量得到明显提高(主频从30 Hz提升至约45 Hz)。
|
下载原图 图 1 尼日尔Agedem地区近地表Q补偿叠前效果对比 Fig. 1 Comparison of near-surface Q compensation pre-stack effect in Agedem area, Niger |
在Q叠前深度偏移实际应用的过程中,首先需要建立准确的深度域速度模型,再通过Q层析或其他方法得到与深度域速度模型相对应的深度域Q模型,最后进行Q叠前深度偏移,因此Q场的准确求取是开展Q叠前偏移的关键。在常规旅行时层析反演过程中,需要建立观测到的旅行时误差与地震射线所穿过介质的慢度的关系方程,再根据网格层析反演的方法求取地下介质每个点的Q值,而Q层析反演需建立观测到的等效Q场(地震波传播过程中Q效应的累计测量)与地下某个度量间隔内的Q值的对应关系,等效Q场定义为
| $ \frac{t_1}{Q_{\text {eff }}}=\sum\limits_{i=1}^n \frac{t_i}{Q_i} $ | (10) |
式中:t1为射线总走时,s;Qeff为等效Q场;Qi为沿射线路径上覆地层第i层介质的Q值;n为射线传播路径上的介质总层数;ti是沿射线路径第i层介质的垂直旅行时,s。
使用初始速度模型、初始Q场共成像点道集进行射线追踪,对于每一条射线,沿着射线路径以及利用初始Q模型的层间Q值,可以累计得到等效Q场的模拟值,从而得到
| $ \frac{t}{Q_{\mathrm{eff}}^{\mathrm{obs}}(t)}-\frac{t}{Q_{\mathrm{eff}}^{\mathrm{mod}}(t)}=\sum\limits_{i, j, k=1}^n\left(t_{i, j, k} \delta Q_{i, j, k}^{-1}\right) $ | (11) |
式中:Qeffobs(t) 为t时刻等效Q场的观测值;Qeffmod(t) 为t时刻等效Q场的模拟值;i,j,k为反演网格的索引;ti, j, k为当前反演网格内的走时,s;δQi, j, k-1为层间值Q-1的修正量,多条射线路径即组成一个稀疏线性矩阵方程组。
定义Q层析的目标函数,求解大型稀疏线性方程组,即
| $ \Delta Q^{-1}=\arg \min _{\Delta Q^{-1}}\left[\left\|L S \Delta Q^{-1}-\Delta t^*\right\|+\mu\left\|\Delta Q^{-1}\right\|\right] $ | (12) |
式中:L为与吸收旅行时相关的反演大型稀疏线性方程组;S为平滑因子;
通过层析反演,得到对于网格单元(i,j,k)中初始Q模型的更新量δQi, j, k-1,通过多次更新得到地下三维Q场。
3 Q叠前深度偏移方法在常规偏移成像过程中,振幅补偿项一般只补偿球面扩散能量损失,而不考虑介质吸收效应对不同频率的能量影响,另外反Q滤波多为一维算法,仅补偿地震波在垂直方向上的振幅损失和相位,而不考虑地震波实际传播路径的差异。
传统积分法深度偏移没有补偿黏弹性介质吸收引起的幅值衰减和频散校正,导致偏移成像分辨率较低。Q叠前深度偏移方法考虑了地震波在传播过程中的介质吸收影响,消除了地震波传播过程中由于介质非弹性引起的地震波吸收衰减和频散问题,得到了垂向分辨率更高的成像结果,同时对吸收造成的能量衰减也进行了一定程度的补偿。
用品质因子Q来描述地下空间介质,一般假定品质因子Q与频率无关,即常Q模型。复速度c(ω) 与实速度vreal(ω) 表达式为
| $ \frac{1}{c(\omega)}=\frac{1}{v_{\text {real }}(\omega)}\left(1-\frac{j}{2 Q}\right) $ | (13) |
如果考虑地震波的速度频散公式,即
| $ v_{\text {real }}(\omega)=v_{\text {real }}\left(\omega_{\text {ref }}\right)\left[1+\frac{1}{\pi Q} \ln \left(\frac{\omega}{\omega_{\text {ref }}}\right)\right] $ | (14) |
式中:ωref为参考频率,Hz;j为虚数单位。
当频率趋向于ωref时,vreal接近于常数,所以可用主频ω0来替代高阶频率ωref,而ω0对应的vreal刚好是通过速度估计方法得到的,式(15)可以变换为
| $ v_{\text {real }}(\omega)=v_{\text {real }}\left(\omega_0\right) \frac{1+\left(\frac{1}{\pi Q}\right) \ln \left(\frac{\omega}{\omega_{\text {ref }}}\right)}{1+\left(\frac{1}{\pi Q}\right) \ln \left(\frac{\omega_0}{\omega_{\text {ref }}}\right)} $ | (15) |
将式(15)代入式(13)可得
| $ \frac{1}{c(\omega)}=\frac{1}{v}\left(1-\frac{j}{2 Q}\right)\left[1-\frac{1}{\pi Q} \ln \left(\frac{\omega}{\omega_0}\right)\right] $ | (16) |
式中:v为常规的偏移速度,m/s;Q表示与频率无关的恒Q值。
对任一地震道d(t),假设常规处理流程中反褶积处理消除了震源子波的影响,应用反褶积成像条件即可得到单道数据的成像结果,即脉冲响应:
| $ I(x, y, z)=\frac{\tau_{\mathrm{g}} r_{\mathrm{s}}^3}{\tau_{\mathrm{s}} r_{\mathrm{g}}^3} \int D(\omega) \omega \exp \left(-j \frac{\pi}{2}\right) \exp\left[j \omega\left(\tau_{\mathrm{s}}+\tau_{\mathrm{g}}\right)-\left(\frac{\tau_{\mathrm{s}}}{Q_{\mathrm{s}}}+\frac{\tau_{\mathrm{g}}}{Q_{\mathrm{g}}}\right) \frac{\ln \left(\frac{\omega}{\omega_0}\right)}{\pi}\right]\exp \left[\frac{\omega}{2}\left(\frac{\tau_{\mathrm{s}}}{Q_{\mathrm{s}}}+\frac{\tau_{\mathrm{g}}}{Q_{\mathrm{g}}}\right)\right] \mathrm{d} \omega $ | (17) |
式中:x,y,z为成像点的三维坐标;D(ω) 为任一地震道d(t) 的傅里叶变换;rs为炮点到成像点的直线距离,m;rg为成像点到检波点的直线距离,m;τs为炮点沿射线路径到成像点的走时,s;τg为成像点沿射线路径到检波点的走时,s;Qs为炮点处与射线路径相关的等效Q值;Qg为检波点处与射线路径相关的等效Q值;τgrs3/τsrg3为成像权系数,补偿了地震波的球面扩散影响。
4 基于井约束的压缩感知叠后拓频方法 4.1 基于井约束的压缩感知叠后拓频方法理论压缩感知作为一种新型采样理论,现已在地震资料处理中获得广泛应用[15]。该理论克服了传统方法中地质参数预构的弊端,基于数据驱动的优点让其在寻找剖面潜力、拓宽频带宽度上限方面发挥了重要作用,可这也对压缩感知拓频方法的保真性带来了一定影响[16]。为消除该影响,提出基于井约束的压缩感知叠后拓频方法,无论在拓频效果还是在结果保真度方面都获得了较好的效果。
压缩感知理论认为一个不满足奈奎斯特采样定理的信号若是稀疏的,则其可以通过某些数学算法恢复为全采样数据[17]。利用如下线性正演模型说明:
| $ y=\boldsymbol{M} x+e $ | (18) |
式中:y为原始地震数据;M表示随机采样矩阵;x为欠采样数据;e代表随机噪声。
根据压缩感知理论可知,若x为稀疏,则其可以被重建为接近y的数据,但由于地震数据普遍复杂多变,无法满足稀疏条件,因此需要借助数学变换对其进行稀疏表示[18]。假设数据x'是数据x在稀疏域F的稀疏表示,则式(18)可以改写为
| $ y=A x^{\prime}+e, A=\boldsymbol{M F}^H $ | (19) |
式中:FH为稀疏变换F的共轭转置矩阵。
若x'中有k个非零元素,且k << L,则视x'稀疏,则可得到重建基函数:
| $ <x>=\arg \min \left\|x^{\prime}\right\|_1 \text { s.t. }\left\|y-A x^{\prime}\right\| \leqslant \eta $ | (20) |
式中:< x >是x'的重建结果;η为自定义恢复误差。
通过求解式(20)中的范数‖x'‖1,找到可以满足误差σ的最稀疏解,然后通过逆稀疏变化得到恢复数据y':
| $ y^{\prime}=\boldsymbol{F}^T <x> $ | (21) |
从地震记录的褶积模型入手来进行压缩感知拓频的研究,假设w为地震子波,r为地下反射系数,g为含噪地震数据,n为随机噪声,含噪地震数据g可表示为
| $ g=w^* r+n $ | (22) |
将式(22)转换到傅里叶域可表示为
| $ G=W R+N=W F r+N $ | (23) |
式中:G,W,R和N分别为g,w,r和n的稀疏域表示。
理想的褶积模型中地下反射系数以脉冲形式,即持续时间趋向于零、带宽趋向于无穷,经过地层吸收、干扰等因素影响得到的一个随机序列,其原本频谱应为全频宽。由于地震子波具有滤波作用(这里子波充当压缩感知理论中的观测矩阵),褶积得到的地震数据就会损失一定的高、低频信息,其频谱也就展现为非全频带形式。在压缩感知理论框架下,首先需要构造满足RIP(有限等距性质)条件的观测矩阵(前人验证随机矩阵具有再利用信号稀疏性和普适性),再利用信号稀疏性,通过求解稀疏正则化的凸优化问题重建缺失数据[19]。由于反射系数在时间域中具有稀疏性,因此将时间域作为稀疏域满足压缩感知重建理论应用的前提条件。基于压缩感知拓频方法也就可以理解为重建被地震子波过滤的反射系数[20]。
在压缩感知理论框架的指导下,将式(23)的欠定方程问题转化为稀疏规则算子约束下的最小误差能量问题:
| $ \min\limits_r \frac{1}{2}\|W F r-G\|_2^2 \text { s.t. }\|r\|_1^1 \leqslant \sigma $ | (24) |
式中:‖·‖2为L2范数约束的误差函数;‖·‖1为L1范数约束的准确解;σ为反射系数的保真性误差估计。
式(24)中第1项为最小误差能量约束,在求解过程中控制重建误差,确保拓频保真性;第2项为稀疏规则算子约束以不断获取稀疏性更好的反射系数r。
为保证保真性,将井数据引入式(24)来约束反演过程,提高反射系数的准确性:
| $ \min\limits_r \frac{1}{2}\|W F r-G\|_2^2+\lambda\left\|r_{\mathrm{w}}-r_{\mathrm{w}}^{\prime}\right\|_2^2 \text { s.t. }\|r\|_1^1 \leqslant \sigma $ | (25) |
式中:rw为井位反射系数;rw'为根据井信息估计的反射系数;λ为正则化参数,用于调节两范数之间的权重以确保稀疏性与保真性之间的平衡。
使用迭代阈值法求解式(25),迭代公式为
| $ \begin{aligned} r^{j+1}= & T_{\lambda_K}\left\{r^j+\frac{1}{\alpha}\left[(W F)^T\left(G-W F r^j\right)+\right.\right. \\ & \left.\left.\lambda R_{\mathrm{w}}^T\left(R_{\mathrm{w}} r^j-r_{\mathrm{w}}^{\prime}\right)\right], \frac{\lambda}{\alpha}\right\} \end{aligned} $ | (26) |
式中:(WF)T为WF的共轭转置;Rw为提取相应井位信息的采样算子。
通过如下迭代阈值法求解式(26)[21]:
初始化:k = 1,赋初始值r0,外循环迭代次数Lin,内循环迭代次数Lout,预设误差ε;
开始迭代:r0 = r0;
外循环:判断
迭代继续:r0 = rk - 1;
内循环:j=1,
执行:
计算拓频后频谱
计算高频补偿后频谱
求得高频补偿数据:
在上述算法中:Tλ为阈值函数;α代表算法参数,α必须大于(WF)TWF的最大特征值;λ用来调整反射系数的稀疏性;L和H分别为提取低频和高频算子。
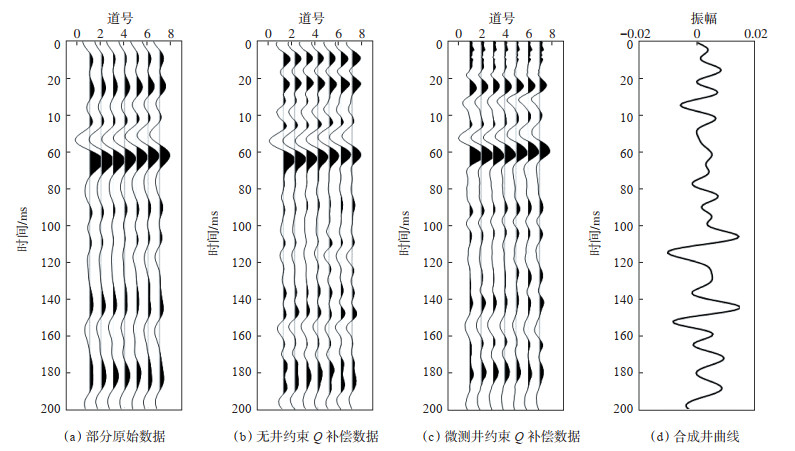
4.2 基于井约束的压缩感知叠后拓频测试为验证井约束稀疏反演的保真优势,同样选用尼日尔Agedem地区部分偏移剖面进行保真性对比试验。如图 2所示,相比于无井约束拓频,有井约束结果与井合成记录更为匹配,20~40 ms层位位置更加准确,在180 ms处,无井约束结果的层位假象问题被解决,总体补偿效果具有更好的保真性。
|
下载原图 图 2 尼日尔Agedem地区近地表Q补偿叠前处理叠加效果对比 Fig. 2 Comparison of stacking effects of near-surface Q compensation pre-stack processing in Agedem area, Niger |
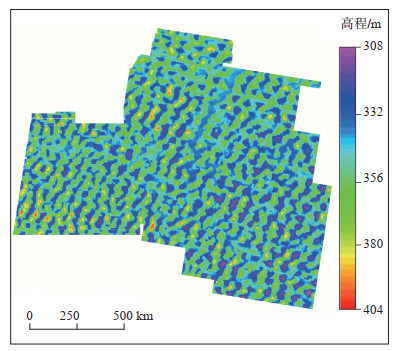
为了验证上述组合高分辨率处理方法在沙漠区的应用效果,选用尼日尔Agedem沙漠区采集的野外地震资料进行应用。Agadem区块位于尼日尔东南部的Termit盆地,面积约27 516 km2,其典型地形条件是起伏的大沙丘,连片工区内地形南北高、中部低,全区范围内沙丘呈南北向条带状分布,海拔为308~404 m,沙丘高度变化大,最高约70 m(图 3)。近地表低降速带大致分为三层结构,全部是黄沙,低速带厚度较大,速度约为300 m/s;降速带厚度变化较大,主要受地表沙丘的影响,速度约为630 m/s。高大沙丘对地震波高频信号吸收衰减作用明显,提高分辨率是本次处理的一项重要工作。
|
下载原图 图 3 尼日尔Agadem地区地表高程图 Fig. 3 Surface elevation map in Agedem area, Niger |
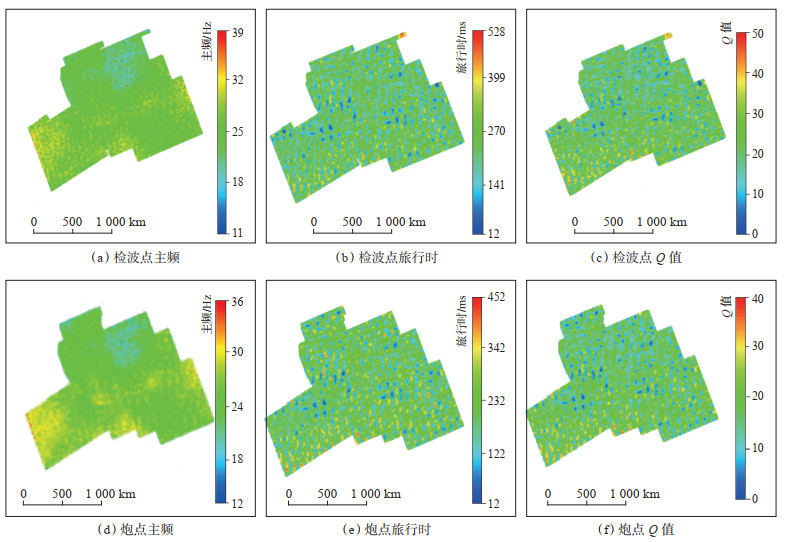
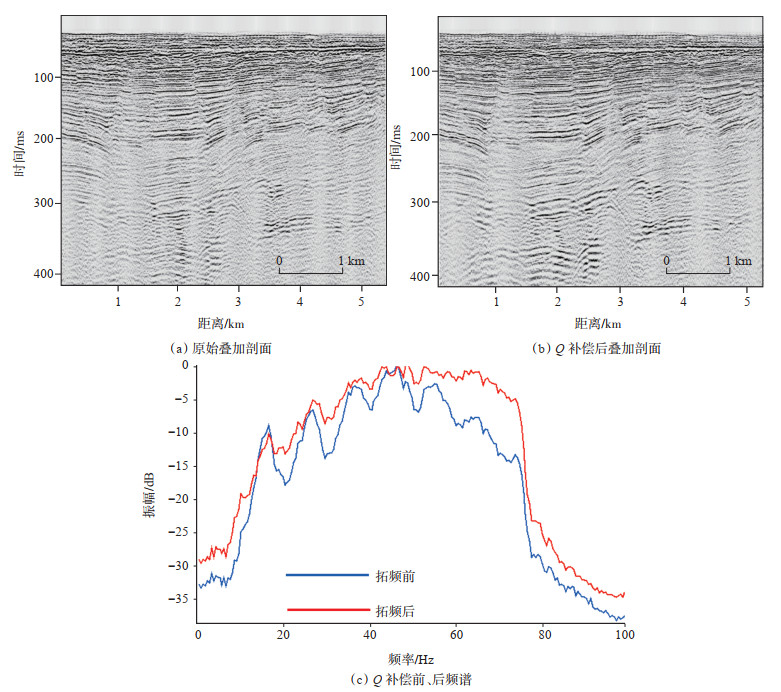
首先,通过分析地震波振幅、主频和表层地震波传播时间等属性,发现表层模型和初至波反演得到的表层相对Q值与属性相关性高,反映了地表对地震波吸收的空间变化(图 4),因此采用了近地表Q补偿,以消除近地表吸收造成的吸收衰减,为精细解释和储层预测提供可靠资料,保证叠加成像。从图 5中可以看出,处理后剖面浅—中层能量增强,深层有效信息增加,能量的补偿有效克服了低降速带的影响,使得层位清晰、断层明显、中深层成像准确。
|
下载原图 图 4 尼日尔Agadem区块地震波平面属性 Fig. 4 Plane attributes of seismic wave in Agedem area, Niger |
|
下载原图 图 5 尼日尔Agadem区块近地表Q补偿前后叠加剖面及频谱 Fig. 5 Stacked sections and spectrum before and after near-surface Q compensation in Agedem area, Niger |
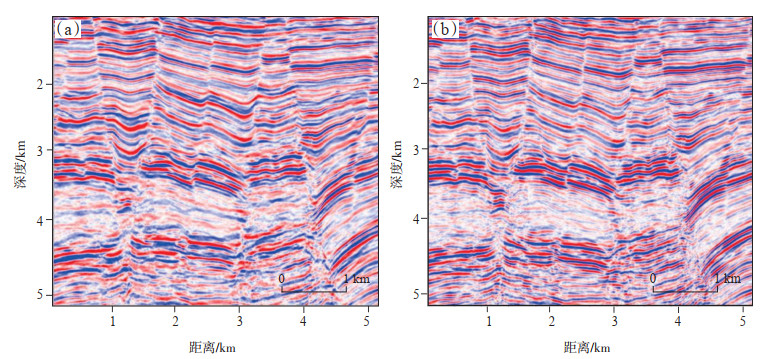
其次,针对底辟构造埋深大、反射能量弱、频带窄的问题,在此Q补偿基础上开展Q叠前深度偏移,消除地震波传播过程中由于介质非弹性因素导致的能量衰减和频散。按波场传播路径完成振幅补偿和相位校正,消除地层吸收效应,得到纵向分辨率更高的成像结果,同时对吸收引起的能量衰减也进行一定程度的补偿。从图 6可以看出,处理后的剖面分辨率显著提高,振幅和相位一致性也得到明显改善,细节成像刻画更为清晰,成像精度更高;强轴之间的目的储层区域分辨率明显提高,由于沙漠区低降速带影响所导致的能量衰减严重问题得到了很好的解决。
|
下载原图 图 6 尼日尔Agadem区块Kirchhoff积分法叠前深度偏移(a)与Q叠前深度偏移(b)效果对比 Fig. 6 Comparison of Kirchhoff integration method (a) and Q-depth migration (b) for pre-stack depth migration in Agedem area, Niger |
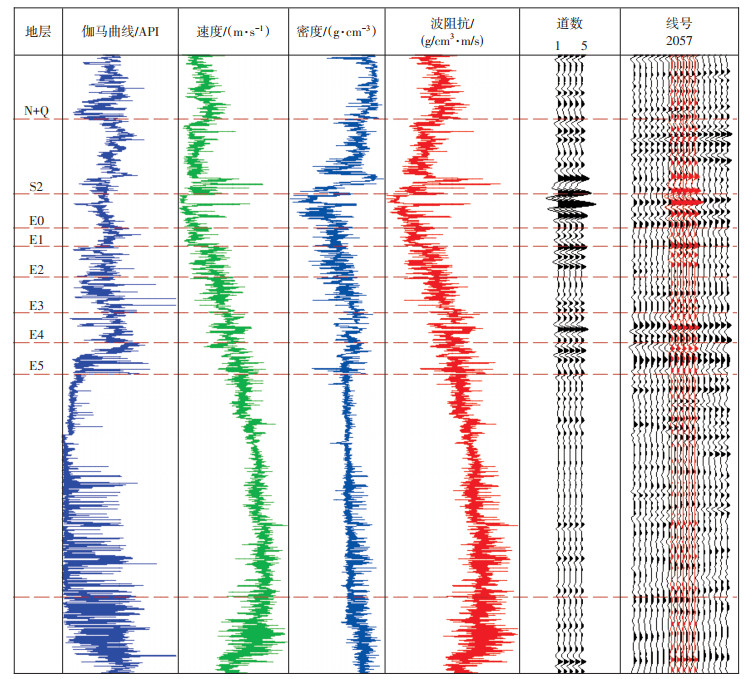
最后,在深度偏移成果上,依据区内已有测井资料,开展基于压缩感知理论的拓频处理,不仅进一步压缩了子波,还加强了全区子波空间的一致性,同时,还提高了井-震分辨率吻合度。利用新资料,开展了多井精细标定,其中DB1井标定后,全井段相关系数大于0.92(图 7),为储层岩性描述和小断层刻画提供了更可靠的数据。
|
下载原图 图 7 尼日尔Agadem区块DB1井合成记录标定 Fig. 7 Calibration of synthetic records of well DB1 in Agedem area, Niger |
通过上述综合高分辨率处理方法,进一步提高了地震资料的纵向分辨率。成果资料显示,断层结构清晰、断面波干脆、小断层错段明显容易识别,为准确落实和精细刻画三维区块内各级断层提供了可靠资料,满足了区域地质研究、区带综合评价、构造精细研究和储量规模预测的地质需求。
6 结论(1)近地表Q补偿时采用双井微测井测量数据求取近地表的实测Q值,恢复了地震波的高频成分,高频能量提升明显,频带宽度有所改善,成像质量大幅提高。
(2)联合应用近地表Q补偿、Q层析及Q叠前深度偏移方法对尼日尔Agedem地区地震资料进行处理后,地震数据的分辨率比常规中深层Q补偿方法和地表一致性反褶积方法高,目的储层区域分辨率明显提高,由于沙漠区低降速带影响所导致的能量衰减严重问题得到很好的解决;在该方法的基础上结合区内已有测井,开展基于压缩感知理论的拓频处理,可进一步压缩子波,全区子波空间一致性更好,提高了纵向分辨率,井-震吻合度更高。
| [1] |
刁瑞. 地震数据提高分辨率处理监控评价技术. 岩性油气藏, 2020, 32(1): 94-101. DIAO Rui. Monitoring and evaluation technology for high resolution processing of seismic data. Lithologic Reservoirs, 2020, 32(1): 94-101. DOI:10.12108/yxyqc.20200110 |
| [2] |
赵岩, 毛宁波, 陈旭. 基于时频域信噪比的自适应增益限反Q滤波方法. 岩性油气藏, 2021, 33(4): 85-92. ZHAO Yan, MAO Ningbo, CHEN Xu. Self-adaptive gain-limit inverse Q filtering method based on SNR in time-frequency domain. Lithologic Reservoirs, 2021, 33(4): 85-92. DOI:10.12108/yxyqc.20210409 |
| [3] |
赵岩, 毛宁波. 基于零偏移距VSP的时变子波反褶积方法. 岩性油气藏, 2019, 31(6): 88-94. ZHAO Yan, MAO Ningbo. Time-varying wavelet deconvolution method based on zero-offset VSP data. Lithologic Reservoirs, 2019, 31(6): 88-94. DOI:10.12108/yxyqc.20190609 |
| [4] |
WANG Yanghua. A stable and efficient approach to inverse Q filtering. Geophysics, 2002, 67(2): 657-663. DOI:10.1190/1.1468627 |
| [5] |
王晓涛, 蒋立, 薛为平, 等. 准噶尔盆地厚沙漠区表层实测Q采集及计算方法研究[R]. 宜昌: 中国石油学会2015年物探技术研讨会, 2015. WANG Xiaotao, JIANG Li, XUE Weiping, et al. Research of measured Q calculation in thick desert area of Junggar Basin [R]. Yichang: 2015 Geophysical Exploration Technology Seminar of Chinese Petroleum Society, 2015. |
| [6] |
蒋立, 罗勇, 程志国, 等. 地表一致性表层相对Q计算及补偿方法研究与应用. 新疆地质, 2015, 33(3): 415-420. JIANG Li, LUO Yong, CHENG Zhiguo, et al. Research and application of surface-consistent relative Q calculation and compensation. Xinjiang Geology, 2015, 33(3): 415-420. DOI:10.3969/j.issn.1000-8845.2015.03.027 |
| [7] |
宋吉杰, 禹金营, 王成, 等. 近地表介质Q估计及其在塔河北部油田的应用. 石油物探, 2018, 57(3): 436-442. SONG Jijie, YU Jinying, WANG Cheng, et al. Q estimation for near-surface media and its application in the northern Tahe Oilfield, China. Geophysical Prospecting for Petroleum, 2018, 57(3): 436-442. DOI:10.3969/j.issn.1000-1441.2018.03.013 |
| [8] |
李伟娜, 云美厚, 党鹏飞, 等. 基于微测井资料的双线性回归稳定Q估计. 石油物探, 2017, 56(4): 483-490. LI Weina, YUN Meihou, DANG Pengfei, et al. Stability Q estimation by dual liner regression based on unhole survey data. Geophysical Prospecting for Petroleum, 2017, 56(4): 483-490. |
| [9] |
韩立国, 张莹, 韩利, 等. 基于压缩感知和稀疏反演的地震数据低频补偿. 吉林大学学报(地球科学版), 2012, 42(增刊3): 259-264. HAN Liguo, ZHANG Ying, HAN Li, et al. Compressed sensing and sparse inversion based low-frequency information compensation of seismic data. Journal of Jilin University(Earth Science Edition), 2012, 42(Suppl 3): 259-264. |
| [10] |
张莹, 基于压缩感知和稀疏反演的低频补偿研究[D]. 长春: 吉林大学, 2013. ZHANG Ying. A Study on low-frequency compensation based on compressed sensing and sparse inversion[D]. Changchun: Jilin University, 2013. |
| [11] |
SUN Miaomiao, LI Zhenchun, LIU Yanli, et al. Low-frequency expansion approach for seismic data based on compressed sensing in low SNR. Applied Sciences, 2021, 11(11): 5028. DOI:10.3390/app11115028 |
| [12] |
苏勤, 曾华会, 田彦灿, 等. 表层Q值确定性求取与空变补偿方法. 石油地球物理勘探, 2019, 54(5): 988-996. SU Qin, ZENG Huahui, TIAN Yancan, et al. Near-surface Q value estimation and quantitative amplitude compensation. Oil Geophysical Prospecting, 2019, 54(5): 988-996. |
| [13] |
凌云, 高军, 吴琳. 时频空间域球面发散与吸收补偿. 石油地球物理勘探, 2005, 40(2): 176-182. LING Yun, GAO Jun, WU Lin. Compensation for spherical dispersion and absorption in time-frequency-space domain. Oil Geophysical Prospecting, 2005, 40(2): 176-182. DOI:10.3321/j.issn:1000-7210.2005.02.018 |
| [14] |
蒋立, 陈勇, 肖艳玲, 等. 地表过渡带近地表Q补偿与地表一致性反褶积处理效果对比研究. 石油物探, 2018, 57(6): 870-877. JIANG Li, CHEN Yong, XIAO Yanling, et al. A comparison of near-surface Q compensation and surface-consistent deconvolution in the near-surface transition zone. Geophysical Prospecting for Petroleum, 2018, 57(6): 870-877. DOI:10.3969/j.issn.1000-1441.2018.06.009 |
| [15] |
BARANIUK R, DAVENPORT M, DEVORE R, et al. A simple proof of the restricted isometry property for random matrices. Constructive Approximation, 2007, 28(3): 253-263. |
| [16] |
KIRACHAIWANICH D, LIANG Qilian. Compressive sensing: To compress or not to compress[R]. Pacific Grove, CA, USA: Proceedings of the Forty-Fifth Asilomar Conference on Signals, Systems and Computers(ASILOMAR), 2011.
|
| [17] |
HERRMANN F J, HENNENFENT G. Non-parametric seismic data recovery with curvelet frames. Geophysical Journal International, 2008, 173(1): 233-248. DOI:10.1111/j.1365-246X.2007.03698.x |
| [18] |
TROPP J A, GILBERT A C. Signal recovery from partial information via orthogonal matching pursuit. IEEE Transactions on Information Theory, 2007, 53(12): 4655-4666. DOI:10.1109/TIT.2007.909108 |
| [19] |
DAVENPORT M A, NEEDELL D, WAKIN M B. Signal space CoSaMP for sparse recovery with redundant dictionaries. IEEE Transactions on Information Theory, 2013, 59(10): 6820-6829. DOI:10.1109/TIT.2013.2273491 |
| [20] |
GORODNITSKI I F, RAO B D. Sparse signal reconstruction from limited data using FOCUSS: A re-weighted norm minimization algorithm. IEEE Transactions on Signal Processing, 1997, 45(3): 600-616. DOI:10.1109/78.558475 |
| [21] |
MOSHTAGHPOUR A, JACQUES L, CAMBARERI V, et al. Consistent basis pursuit for signal and matrix estimates in quantized compressed sensing. IEEE Signal Processing Letters, 2016, 23(1): 25-29. |
 2023, Vol. 35
2023, Vol. 35




