2. 中国石油大学 (北京)油气资源与探测国家重点实验室, 北京 102249
2. State Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum(Beijing), Beijing 102249, China
火山岩油藏岩石物性、成藏机理与砂岩油藏大不相同,其储层裂缝发育,具有产能分布复杂、产量递减快、无稳产期、见水特征多样、井间干扰严重、衰竭式开发采收率低等开发特征[1-2]。因此,火山岩油藏产能分析和预测具有重要意义。
近年来大量的国内外学者建立了众多数学模型来描述裂缝性油藏的渗流问题。自20世纪,Larsen等[3]和Guo等[4]推导出了有限导流能力垂直裂缝水平井压力模型和产能模型,但未考虑裂缝与裂缝之间的干扰;郎兆新等[5]推导出压裂水平井产量计算公式,得到了产量和生产压降与裂缝长度和裂缝条数的关系;程林松等[6]推导出了分支水平井流场分布和产能计算公式;Horne等[7]基于Guo的模型,考虑了裂缝之间的相互干扰,并进行了进一步推导;范子菲等[8]推导出裂缝性油藏水平井稳态公式,且考虑到了油层的各向异性和裂缝部分穿透油层;宁正福等[9]基于文献[6]对水平井产能预测公式进行了重新推导和修正,考虑了裂缝内存在渗流阻力和压力损失;Zerzar等[10]建立了考虑射孔影响的水平井流态模型;郭肖等[11]研究了应力敏感和启动压力梯度对低渗透气藏水平井产能的影响;Valko等[12]着手于压裂水平井压力分布模型的建立和求解,且考虑到了裂缝与裂缝之间的影响。Bello等[13]将次生裂缝简化成双重介质模型[14],建立了双线性流模型;Brown等[15]建立了三线性流模型,将油藏渗流分为3个区域,即人工裂缝区、主裂缝之间的体积压裂区和未压裂区;姚军等[16]在Brown模型的基础上,建立了含有启动压力梯度的三线性流模型;苏玉亮等[17]进一步推广了三线性流模型,着重研究了压裂缝网参数对产量的影响,但这些模型均未考虑到储层的应力敏感性。
火山岩产能预测除了解析与半解析方法,还有数值模拟和一些人工智能的方法。潘有军等[18]采用归一化处理和多元线性回归法预测火山岩油藏油井压裂后的初期产能,但对于产能影响因素的敏感性无法判断。苏皓等[19]基于离散裂缝模型的数值模拟方法建立了体积压裂水平井模拟模型,但数值模拟方法很难考虑非常规储层的渗流机理。宋宣毅等[20]通过机器学习的算法建立了产能预测的模型,但没有考虑油藏渗流规律上的影响因素。
本文考虑油藏渗流的启动压力梯度和应力敏感特征,建立火山岩油藏分区产能模型,得到拉氏空间压裂水平井复合流动模型,并对新疆油田某区块进行模型验证,最后对各区主要影响因素进行敏感性分析,以期为火山岩油藏的开发提供有价值的指导。
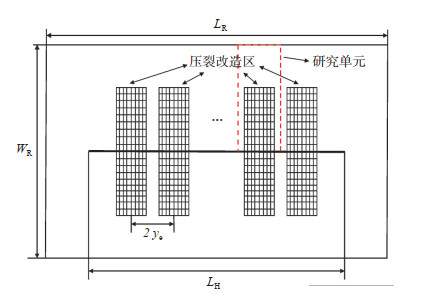
1 物理模型和假设条件设某压裂盒状火山岩油藏,储层内发育天然裂缝,水平井位于油藏中心,根据井筒的对称性,选择如图 1所示的流动单元(单条裂缝控制区域)。图 1中油藏长度为LR,m;油藏宽度为WR,m;水平井长度为LH,m;裂缝间距为2ye,m。
|
下载原图 图 1 火山岩油藏压裂水平井缝网改造模型 Fig. 1 Modification model of fracture network of fractured horizontal well in volcanic reservoirs |
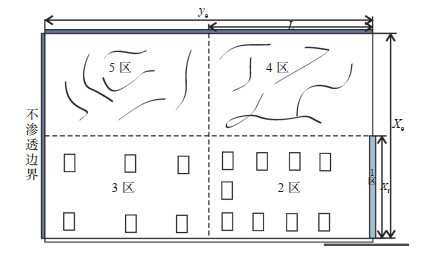
如图 2所示,本文油藏渗流模型基于WarrenRoot模型。将压裂后的储层划分为5个区域:区域1(0 ≤ x ≤ xf,0 ≤ y ≤ w/2)为人工裂缝区(HF区),可近似为单重介质线性流;区域2(0 ≤ x ≤ xf,w/2 ≤ y ≤ L)为缝网改造区(FSRV区);区域3(0 ≤ x ≤ xe,w/2 ≤ y ≤ ye)为部分缝网改造区(PSRV区);区域4(xf ≤ x ≤ xe,w/2 ≤ y ≤ ye)和区域5(xf ≤ x ≤ xe,L ≤ y ≤ ye)均为未改造区(USRV区),采用双重介质表征,其中孔隙和天然裂缝为储集空间,人工裂缝为流动通道。
|
下载原图 图 2 压裂水平井缝网改造五区流动模型示意图 Fig. 2 Schematic diagram of five-zone flow model for fracture network reformation of fractured horizontal wells |
模型的其他假设条件为:
(1)油藏外边界封闭,原始地层压力为pe,储层厚度为h,储层中部一口压裂水平井,考虑2种工作制度:定压情况和定产情况;
(2)各条主裂缝等间距分布且性质相同,主裂缝高度等于储层厚度,相邻2条主裂缝间的中间位置为不渗透流动边界;
(3)流体流动为单相非稳态流动,不考虑重力、毛管压力和井筒中的阻力;
(4)流体从USRV区流入FSRV区和PSRV区再流入HF区,最后流入水平井;
(5)整个区域内由应力敏感性导致的渗透率变化不可忽略;在USRV区内,临界压力梯度不可忽略。
在整个区域,裂缝渗透性随着地层压力的降低而降低,考虑到应力敏感作用,遵循Kikani和Pedrosa[21]所提出的应力敏感规律,通常用渗透率模量γ来表征储层渗透率随地层压力的变化程度:
| $ \gamma=\frac{1}{k} \frac{\mathrm{d} k}{\mathrm{~d} P} $ | (1) |
式中:γ为渗透率模量,MPa-1;k为渗透率,mD;P为压降,MPa。
在USRV区,地层具有超低渗透性的微小孔喉,其非达西流动是由临界压力梯度引起的。因此,本文选择拟启动压力梯度方法来描述非达西流,表示为
| $ v= \begin{cases}-\frac{3.6 k}{\mu}\left[\operatorname{grad}(P)-\lambda_{\mathrm{m}}\right] & \operatorname{grad}(P)>\lambda_{\mathrm{m}} \\ 0 & \operatorname{grad}(P)<\lambda_{\mathrm{m}}\end{cases} $ | (2) |
式中:v为渗流速度,m/h;λm是启动压力梯度,MPa/m;μ为黏度,mPa·s。
2 数学模型及其求解 2.1 无量纲参数在物理模型和假设条件的基础上,为了便于理解和推导,对无量纲参数进行定义,如表 1所列。
|
|
下载CSV 表 1 无量纲参数 Table 1 Dimensionless parameters |
(1)USRV区的数学模型
将USRV区5视为双重介质,根据质量守恒原理,可以得到双重介质系统的连续性方程。在区域4和5中,假设这些区域在X方向上只有一维线性流,此外,根据等式使用启动压力梯度来描述非达西流,可以表示为
| $ v=-\frac{3.6 k_{i \mathrm{f}}}{\mu}\left[\operatorname{grad}\left(p_{i \mathrm{f}}\right)-\lambda_{\mathrm{m}}\right] $ | (3) |
根据渗透率模量的定义,当生产过程中地层压力降低时,渗透率应力敏感性不能忽略,可表示为
| $ k=k_{\mathrm{e}} e^{-\gamma\left(p_{\mathrm{e}}-p\right)} $ | (4) |
式中:p为目前地层压力,MPa;ke为初始条件下的渗透率,mD。
如图 2所示,区域5的外边界是不渗透的,其内边界是区域3的外边界。因此,外部边界为非流动边界,内部边界中区域3和区域5之间的压力相等。结合初始条件和边界条件,可以得到区域5的无量纲数学模型:
| $ \left\{\begin{array}{l} e^{-\gamma_{\mathrm{D}} p_{5 \mathrm{fD}}} \frac{\partial^{2} p_{5 \mathrm{fD}}}{\partial x_{\mathrm{D}}^{2}}-\gamma_{\mathrm{D}} \lambda_{\mathrm{mD}} \frac{\partial p_{5 \mathrm{fD}}}{\partial x_{\mathrm{D}}}+\lambda_{5}\left(p_{5 \mathrm{mD}}-p_{5 \mathrm{fD}}\right)=\frac{\omega_{5}}{\eta_{5 \mathrm{D}}} \frac{\partial p_{5 \mathrm{D}}}{\partial t_{\mathrm{D}}}\\ \frac{1-\omega_{5}}{\eta_{5 \mathrm{D}}} \frac{\partial p_{5 \mathrm{mD}}}{\partial t_{\mathrm{D}}}+\lambda_{5}\left(p_{5 \mathrm{mD}}-p_{5 \mathrm{fD}}\right)=0 \\ \left.\frac{\partial p_{5 \mathrm{fD}}}{\partial x_{\mathrm{D}}}\right|_{x_{\mathrm{D}}=x_{\mathrm{eD}}}=0 \\ \left.p_{5 \mathrm{fD}}\right|_{x_{\mathrm{D}}=1}=\left.p_{3 \mathrm{fD}}\right|_{x_{\mathrm{D}}=1} \end{array}\right. $ | (5) |
由于区域4和5都是USRV区,并且具有相同的属性,因此采用与区域5相同的方法,考虑到边界条件和初始条件,可以得到区域4的无量纲数学模型:
| $ \left\{\begin{array}{l} e^{-\gamma_{\mathrm{D}} p_{4 \mathrm{fD}}} \frac{\partial^{2} p_{4 \mathrm{fD}}}{\partial x_{\mathrm{D}}^{2}}-\gamma_{\mathrm{D}} \lambda_{\mathrm{mD}} \frac{\partial p_{4 \mathrm{fD}}}{\partial x_{\mathrm{D}}}+\lambda_{4}\left(p_{4 \mathrm{mD}}-p_{4 \mathrm{fD}}\right)=\frac{\omega_{4}}{\eta_{4 \mathrm{D}}} \frac{\partial p_{4 \mathrm{fD}}}{\partial t_{\mathrm{D}}}\\ \frac{1-\omega_{4}}{\eta_{4 \mathrm{D}}} \frac{\partial p_{4 \mathrm{mD}}}{\partial t_{\mathrm{D}}}+\lambda_{4}\left(p_{4 \mathrm{mD}}-p_{4 \mathrm{fD}}\right)=0 \\ \left.\frac{\partial p_{4 \mathrm{fD}}}{\partial x_{\mathrm{D}}}\right|_{x_{\mathrm{D}}=x_{\mathrm{eD}}}=0 \\ \left.p_{4 \mathrm{fD}}\right|_{x_{\mathrm{D}}=1}=\left.p_{2 \mathrm{fD}}\right|_{x_{\mathrm{D}}=1} \end{array}\right. $ | (6) |
(2)PSRV区的数学模型
在PSRV区,流体流动遵循达西定律。假设Y方向为线性流动,并考虑应力敏感性。外边界是储层的边界,即非流动边界。内边界两侧的压力相等。结合初始条件和边界条件,考虑从区域5流入区域3的流体。无量纲模型为
| $ \left\{\begin{array}{l} e^{-\gamma_{\mathrm{D}} p_{3 \mathrm{fD}}} \frac{\partial^{2} p_{3 \mathrm{fD}}}{\partial y_{\mathrm{D}}^{2}}+\left.\frac{k_{5 \mathrm{fe}}}{k_{3 \mathrm{fe}}} e^{-\gamma_{\mathrm{D}} p_{\mathrm{5fD}}}\left(\frac{\partial p_{5 \mathrm{f} \mathrm{D}}}{\partial x_{\mathrm{D}}}+G\right)\right|_{x_{\mathrm{D}}=1}+\lambda_{3}\left(p_{3 \mathrm{mD}}-p_{3 \mathrm{fD}}\right)=\frac{\omega_{3}}{\eta_{3 \mathrm{D}}} \frac{\partial p_{3 \mathrm{fD}}}{\partial t_{\mathrm{D}}}\\ \frac{1-\omega_{3}}{\eta_{3 \mathrm{D}}} \frac{\partial p_{3 \mathrm{mD}}}{\partial t_{\mathrm{D}}}+\lambda_{3}\left(p_{3 \mathrm{mD}}-p_{3 \mathrm{fD}}\right)=0 \\ \left.\frac{\partial p_{3 \mathrm{fD}}}{\partial y_{\mathrm{D}}}\right|_{y_{\mathrm{p}}=y_{\mathrm{eD}}}=0 \\ \left.p_{3 \mathrm{D}}\right|_{y_{\mathrm{p}}=L}=\left.p_{2 \mathrm{fD}}\right|_{y_{\mathrm{D}}=L} \end{array}\right. $ | (7) |
式中:G为重力加速度,m2/s。
(3)FSRV区的数学模型
假设Y方向为线性流,并遵循类似的推导过程(如区域3),但考虑流量守恒的外部边界除外。考虑从区域4流入区域2的流体,描述区域2流动的无因次渗流模型为
| $ \left\{\begin{array}{l} e^{-\gamma_{\mathrm{D}} p_{2 \mathrm{fD}}} \frac{\partial^{2} p_{2 \mathrm{fD}}}{\partial y_{\mathrm{D}}^{2}}+\left.\frac{k_{4 \mathrm{fe}}}{k_{2 \mathrm{fe}}} e^{-\gamma_{\mathrm{D}} P_{4 \mathrm{fD}}}\left(\frac{\partial p_{4 \mathrm{fD}}}{\partial x_{\mathrm{D}}}+G\right)\right|_{x_{\mathrm{D}}=1}+\lambda_{2}\left(p_{2 \mathrm{mD}}-p_{2 \mathrm{fD}}\right)=\frac{\omega_{3}}{\eta_{2 \mathrm{D}}} \frac{\partial p_{2 \mathrm{fD}}}{\partial t_{\mathrm{D}}}\\ \frac{1-\omega_{2}}{\eta_{2 \mathrm{D}}} \frac{\partial p_{2 \mathrm{mD}}}{\partial t_{\mathrm{D}}}+\lambda_{3}\left(p_{2 \mathrm{mD}}-p_{2 \mathrm{fD}}\right)=0 \\ \left.e^{-\gamma_{\mathrm{D}} p_{2 \mathrm{fD}}} \frac{\partial^{2} p_{2 \mathrm{fD}}}{\partial y_{\mathrm{D}}^{2}}\right|_{y_{\mathrm{D}}=L_{\mathrm{D}}}=\left.\frac{1}{M_{32}} e^{-\gamma_{\mathrm{D}} p_{2 \mathrm{fD}}} \frac{\partial^{2} p_{2\mathrm{fD}}}{\partial y_{\mathrm{D}}^{2}}\right|_{y_{\mathrm{D}}=L_{\mathrm{D}}} \\ \left.p_{2 \mathrm{D}}\right|_{y_{\mathrm{D}}}=\frac{w_{\mathrm{D}}}{2}=\left.p_{1 \mathrm{fD}}\right|_{y_{\mathrm{D}}}=\frac{w_{\mathrm{D}}}{2} \end{array}\right. $ | (8) |
式中:M32表示3区和2区的流度比,M32 =
(4)HF区的数学模型
HF区的流体流动也假设为X方向的线性流。考虑到应力敏感性的影响,人工裂缝中的流量控制方程为
| $ \left\{\begin{array}{l} e^{-\gamma_{\mathrm{D}} p_{1 \mathrm{fD}}} \frac{\partial^{2} p_{1 \mathrm{fD}}}{\partial x_{\mathrm{D}}^{2}}+\left.\frac{2}{C_{\mathrm{FD}}} e^{-\gamma_{\mathrm{D}} p_{2 \mathrm{fD}}} \frac{\partial p_{2\mathrm{fD}}}{\partial y_{\mathrm{D}}}\right|_{y_{\mathrm{D}}=\frac{w_{\mathrm{D}}}{2}}=\frac{1}{\eta_{1 \mathrm{D}}} \frac{\partial p_{1 \mathrm{fD}}}{\partial t_{\mathrm{D}}} \\ \left.e^{-\gamma_{\mathrm{D}} p_{1 \mathrm{fD}}} \frac{\partial p_{1 \mathrm{fD}}}{\partial x_{\mathrm{D}}}\right|_{x_{\mathrm{D}}=0}=-\frac{\varPi}{C_{\mathrm{FD}}} \\ \left.\frac{\partial p_{1 \mathrm{fD}}}{\partial x_{\mathrm{D}}}\right|_{x_{\mathrm{D}}=1}=0 \end{array}\right. $ | (9) |
上面的模型是定产条件下的数学模型,当考虑定压条件下,只有边界条件发生改变:
| $ \left.e^{-\gamma_{\mathrm{D}} p_{1\mathrm{fD}}} \frac{\partial p_{1 \mathrm{fD}}}{\partial x_{\mathrm{D}}}\right|_{x_{\mathrm{D}}=0}=-\frac{\varPi}{C_{\mathrm{FD}}} \bar{q}_{\mathrm{FD}} $ | (10) |
式中:qˉFD代表拉普拉斯域下的单条裂缝产量,m3/d。
2.3 模型求解由于应力敏感,整个区域的方程都是强非线性的,利用Kikani等[21]的代换和拉普拉斯变换消除非线性,可以得到拉普拉斯域的井底压力解:
| $ p_{j \mathrm{D}}=-\frac{1}{\gamma_{\mathrm{D}}} \ln \left(1-\gamma_{\mathrm{D}} \xi_{j \mathrm{D}}\right), j=1, 2, 3, 4, 5 $ | (11) |
并引入以下摄动变换公式:
| $ \xi_{j \mathrm{D}}=\xi_{j \mathrm{D0}}+\xi_{j \mathrm{Dl}}+\xi_{j \mathrm{D2}}+\cdots, j=1, 2, 3, 4, 5 $ | (12) |
| $ \frac{1}{1-\gamma_{\mathrm{D}} \xi_{j \mathrm{D}}}=1+\gamma_{\mathrm{D}} \xi_{j \mathrm{D}}+\gamma_{\mathrm{D}}^{2} \xi_{j \mathrm{D}}^{2}+\cdots, j=1, 2, 3, 4, 5 $ | (13) |
| $ \begin{gathered} -\frac{1}{\gamma_{\mathrm{D}}} \ln \left(1-\gamma_{\mathrm{D}} \xi_{j \mathrm{D}}\right)=\gamma_{\mathrm{D}} \xi_{j \mathrm{D}}+\frac{1}{2} \gamma_{\mathrm{D}} \xi_{j \mathrm{D}}^{2}+\cdots, \\ j=1, 2, 3, 4, 5 \end{gathered} $ | (14) |
因为无因次渗透率模量较小,所以只要零阶摄动解就可以满足计算的精度要求。另外,拉普拉斯变换可以将偏微分方程转化为常微分方程。通过上述分析,可以得到变换后的解。由于定产和定压2种情况的区别是区域1的内边界不同,所以求解过程相似,以定产情况为例来描述求解过程。区域5— 1的无因次渗流模型分别为
| $ \left\{\begin{array}{l} \frac{\partial^{2} \overline{\xi_{5 \mathrm{D} 0}}}{\partial x_{\mathrm{D}}^{2}}-\frac{\partial \overline{\xi_{5 \mathrm{D} 0}}}{\partial x_{\mathrm{D}}}-f_{\mathrm{s} 5} \overline{\xi_{5 \mathrm{D} 0}}=0 \\ \left.\frac{\partial \overline{\xi_{5 \mathrm{D} 0}}}{\partial x_{\mathrm{D}}}\right|_{x_{\mathrm{D}}=x_{\mathrm{eD}}}=0 \\ \left.\overline{\xi_{5 \mathrm{D} 0}}\right|_{x_{\mathrm{D}}=1}=\left.\overline{\xi_{3 \mathrm{D} 0}}\right|_{x_{\mathrm{D}}=1} \end{array}\right. $ | (15) |
| $ \left\{\begin{array}{l} \frac{\partial^{2} \overline{\xi_{4 \mathrm{D} 0}}}{\partial x_{\mathrm{D}}^{2}}-\frac{\partial \overline{\xi_{4 \mathrm{D} 0}}}{\partial x_{\mathrm{D}}}+\lambda_{4}\left(p_{4 \mathrm{mD}}-p_{4 \mathrm{fD}}\right)-f_{\mathrm{s} 4} {\overline{\xi_{4 \mathrm{D} 0}}}=0 \\ \left.\frac{\partial \overline{\xi_{\mathrm{4D} 0}}}{\partial x_{\mathrm{D}}}\right|_{x_{\mathrm{D}}=x_{\mathrm{eD}}}=0 \\ \left.\overline{\xi_{4 \mathrm{D} 0}}\right|_{x_{\mathrm{D}}=1}=\left.\overline{\xi_{2 \mathrm{D} 0}}\right|_{x_{\mathrm{D}}=1} \end{array}\right. $ | (16) |
| $ \left\{\begin{array}{l} \frac{\partial^{2} \overline{\xi_{3 \mathrm{D} 0}}}{\partial y_{\mathrm{D}}^{2}}+\left.\frac{k_{5 \mathrm{f}i}}{k_{3 \mathrm{f} i}}\left(\frac{\partial \overline{\xi_{5 \mathrm{D} 0}}}{\partial x_{\mathrm{D}}}+\frac{G}{s}\right)\right|_{x_{\mathrm{D}}=1}-f_{\mathrm{s} 3} \overline{\xi_{3 \mathrm{D} 0}}=0 \\ \left.\frac{\partial \overline{\xi_{3 \mathrm{D} 0}}}{\partial y_{\mathrm{D}}}\right|_{y_{\mathrm{D}}=y_{\mathrm{eD}}}=0 \\ \left.\overline{\xi_{3 \mathrm{D}0}}\right|_{y_{\mathrm{D}}=L}=\left.\overline{\xi_{2 \mathrm{D} 0}}\right|_{y_{\mathrm{D}}=L} \end{array}\right. $ | (17) |
| $ \left\{\begin{array}{l} e^{-\gamma_{\mathrm{D}} p_{2 \mathrm{fD}}} \frac{\partial^{2} \overline{\xi_{2 \mathrm{D} 0}}}{\partial y_{\mathrm{D}}^{2}}+\left.\frac{k_{4 \mathrm{f} i}}{k_{2 \mathrm{f} i}}\left(\frac{\partial \overline{\xi_{2 \mathrm{D} 0}}}{\partial x_{\mathrm{D}}}+\frac{G}{s}\right)\right|_{x_{\mathrm{D}}=1}-f_\mathrm{s2}\overline{\xi_{2 \mathrm{D} 0}}=0 \\ \left.\frac{\partial \overline{\xi_{2 \mathrm{D} 0}}}{\partial y_{\mathrm{D}}}\right|_{y_{\mathrm{D}}=L_{\mathrm{D}}}=\left.\frac{1}{M_{32}} \frac{\partial \overline{\xi_{3 \mathrm{D} 0}}}{\partial y_{\mathrm{D}}}\right|_{y_{\mathrm{D}}=L_{\mathrm{D}}} \\ \left.\overline{\xi_{2 \mathrm{D0}}}\right|_{y_{\mathrm{D}}=\frac{w_{\mathrm{D}}}{2}}=\left.\overline{\xi_{1 \mathrm{D} 0}}\right|_{y_{\mathrm{D}}=\frac{w_{\mathrm{D}}}{2}} \end{array}\right. $ | (18) |
| $ \left\{\begin{array}{l} \frac{\partial^{2} \overline{\xi_{1 \mathrm{D} 0}}}{\partial x_{\mathrm{D}}^{2}}+\left.\frac{2}{C_{\mathrm{FD}}} \frac{\partial \overline{\xi_{2 \mathrm{D0}}}}{\partial y_{\mathrm{D}}}\right|_{y_{\mathrm{D}}=\frac{w_{\mathrm{D}}}{2}}-s \overline{\xi_{1 \mathrm{D} 0}}=0 \\ \left.\frac{\partial \overline{\xi_{1 \mathrm{D} 0}}}{\partial x_{\mathrm{D}}}\right|_{x_{\mathrm{D}}=0}=-\frac{\varPi}{C_{\mathrm{FD}} s} \\ \left.\frac{\partial \overline{\xi_{1 \mathrm{D} 0}}}{\partial x_{\mathrm{D}}}\right|_{x_{\mathrm{D}}=1}=0 \end{array}\right. $ | (19) |
其中:s是拉普拉斯参数。为了简化,用fs i代替部分公式:
| $ f_{\mathrm{s} i}=\frac{\lambda_{i}\left(1-w_{i}\right) s}{\lambda_{i} \eta_{i \mathrm{D}}+\left(1-w_{i}\right) s}+\frac{w_{i} s}{\eta_{i \mathrm{D}}}, i=2, 3, 4, 5 $ | (20) |
然后在拉普拉斯域分别求解方程(14)和方程(15)中的模型,得到如下解:
| $ \overline{\xi_{4 \mathrm{D} 0}}=\left.\frac{\left(-\frac{m_{2}}{m_{1}}\right) e^{m_{1}\left(x_{\mathrm{D}}-x_{\mathrm{eD}}\right)}+e^{m_{2}\left(x_{\mathrm{D}}-x_{\mathrm{eD}}\right)}}{\left(-\frac{m_{2}}{m_{1}}\right) e^{m_{1}\left(1-x_{\mathrm{eD}}\right)}+e^{m_{2}\left(1-x_{\mathrm{eD}}\right)}} \overline{\xi_{2 \mathrm{D0}}}\right|_{x_{\mathrm{D}}=1} $ | (21) |
| $ \overline{\xi_{5 \mathrm{D} 0}}=\left.\frac{\left(-\frac{r_{2}}{r_{1}}\right) e^{r_{2}\left(x_{\mathrm{D}}-x_{\mathrm{eD}}\right)}+e^{r_{2}\left(x_{\mathrm{D}}-x_{\mathrm{e} \mathrm{D}}\right)}}{\left(-\frac{r_{2}}{r_{1}}\right) e^{r_{1}\left(1-x_{\mathrm{ed}}\right)}+e^{r_{2}\left(1-x_{\mathrm{eD}}\right)}} \overline{\xi_{3 \mathrm{D} 0}}\right|_{x_{\mathrm{D}}=1} $ | (22) |
其中:
| $ m_{1}=\frac{\lambda_{\mathrm{D}}+\gamma_{\mathrm{D}} G+\sqrt{\left(\lambda_{\mathrm{D}}+\gamma_{\mathrm{D}} G\right)^{2}+4 f_{\mathrm{s} 4}}}{2} $ | (23) |
| $ m_{2}=\frac{\lambda_{\mathrm{D}}+\gamma_{\mathrm{D}} G-\sqrt{\left(\lambda_{\mathrm{D}}+\gamma_{\mathrm{D}} G\right)^{2}+4 f_{\mathrm{s} 4}}}{2} $ | (24) |
| $ r_{1}=\frac{\lambda_{\mathrm{D}}+\gamma_{\mathrm{D}} G+\sqrt{\left(\lambda_{\mathrm{D}}+\gamma_{\mathrm{D}} G\right)^{2}+4 f_{\mathrm{s} 5}}}{2} $ | (25) |
| $ r_{2}=\frac{\lambda_{\mathrm{D}}+\gamma_{\mathrm{D}} G-\sqrt{\left(\lambda_{\mathrm{D}}+\gamma_{\mathrm{D}} G\right)^{2}+4 f_{\mathrm{s} 5}}}{2} $ | (26) |
将式(20)代入式(16),区域3的解为
| $ \begin{aligned} \overline{\xi_{3 \mathrm{D0}}}=& \frac{\cosh \left[\sqrt{c_{1}}\left(y_{\mathrm{D}}-y_{\mathrm{eD}}\right)\right]}{\cosh \left[\sqrt{c_{1}}\left(L_{\mathrm{D}}-y_{\mathrm{eD}}\right)\right]}\left(\left.\overline{\xi_{2 \mathrm{D} 0}}\right|_{y_{\mathrm{D}}=L}-\frac{k_{5 \mathrm{fe}}}{k_{3 \mathrm{fe}} c_{1}}+\frac{G}{s}\right)+\\ & \frac{k_{\mathrm{fe}}}{k_{3 \mathrm{fe}} c_{1}} \frac{G}{s} \end{aligned} $ | (27) |
其中:c1 =
将式(20)代入式(17)得到区域2的解,然后利用这些解导出区域1的解,进一步得到拉普拉斯域的无量纲井底压力。
| $ \overline{\xi_{1 \mathrm{D} 0}}=\frac{\varPi \cosh \left[\sqrt{c_{3}}\left(x_{\mathrm{D}}-1\right)\right]}{C_{\mathrm{FD}} s \sqrt{c_{3}} \sinh \left(\sqrt{c_{3}}\right)}+\frac{2 B}{C_{\mathrm{FD}}}\left(\frac{k_{4 \mathrm{e}}}{k_{2 \mathrm{fe}} c_{2}}-\frac{k_{5 \mathrm{fe}}}{k_{3 \mathrm{fe}} c_{1}}\right) \frac{G}{s c_{3}}+\frac{2 A}{C_{\mathrm{FD}}} \frac{k_{4 \mathrm{fe}}}{k_{2 \mathrm{fe}} c_{2}} \frac{G}{s c_{3}} $ | (28) |
| $ \bar{p}_{\mathrm{wD0}}=\overline{\xi_{1 \mathrm{D}0}}\left(x_{\mathrm{D}}=0\right) \frac{\varPi}{C_{\mathrm{FD}} s \sqrt{c_{3}} \tanh \left(\sqrt{c_{3}}\right)}+\frac{2 B}{C_{\mathrm{FD}}}\left(\frac{k_{4 \mathrm{fe}}}{k_{2 \mathrm{fe}} c_{2}}-\frac{k_{5 \mathrm{fe}}}{k_{3 \mathrm{e}} c_{1}}\right) \frac{G}{s c_{3}}+\frac{2 A}{C_{\mathrm{FD}}} \frac{k_{4 \mathrm{fe}}}{k_{2 \mathrm{e}} c_{2}} \frac{G}{s c_{3}} $ | (29) |
其中,定义c3=
| $ A=\frac{-\sqrt{c_{2}} \sinh \left[\sqrt{c_{2}}\left(\frac{w_{\mathrm{D}}}{2}-L_{\mathrm{D}}\right)\right]+c_{0} \sqrt{c_{2}} \cosh \left[\sqrt{c_{2}}\left(\frac{w_{\mathrm{D}}}{2}-L_{\mathrm{D}}\right)\right]}{\cosh \left[\sqrt{c_{2}}\left(\frac{w_{\mathrm{D}}}{2}-L_{\mathrm{D}}\right)\right]+c_{0} \sinh \left[\sqrt{c_{2}}\left(\frac{w_{\mathrm{D}}}{2}-L_{\mathrm{D}}\right)\right]} $ | (30) |
| $ B=\frac{c_{0} \sqrt{c_{2}}}{\cosh \left[\sqrt{c_{2}}\left(\frac{w_{\mathrm{D}}}{2}-L_{\mathrm{D}}\right)\right]+c_{0} \sinh \left[\sqrt{c_{2}}\left(\frac{w_{\mathrm{D}}}{2}-L_{\mathrm{D}}\right)\right]} $ | (31) |
| $ c_{0}=\frac{\sqrt{c_{1}} \tan h\left[\sqrt{c_{1}}\left(L_{\mathrm{D}}-y_{\mathrm{eD}}\right)\right]}{M_{32} \sqrt{c_{2}}} $ | (32) |
| $ c_{2}=\frac{k_{4 \mathrm{e}}}{k_{2 \mathrm{fe}}} \beta_{1}+f_{\mathrm{s} 2} $ | (33) |
考虑实际生产的情况,还要考虑表皮系数(S)和井筒储存效应(CD),根据Duhamel原理,井底压力为
| $ \bar{p}_{\mathrm{wD}}\left(C_{\mathrm{D}}, S\right)=\frac{s \bar{p}_{\mathrm{wD} 0}+S}{s\left[1+C_{\mathrm{D}} s\left(s \bar{p}_{\mathrm{wD0}}+S\right)\right]} $ | (34) |
将Sthefest数值反演式采用摄动变换法求解实际井底压力:
| $ p_{\mathrm{wD}}=-\frac{\ln \left[1-\gamma_{\mathrm{D}} L^{-1}\left(\bar{p}_{\mathrm{wD0}}\right)\right]}{\gamma_{\mathrm{D}}} $ | (35) |
同理,可以求出定压条件下的无量纲产量的拉氏解为
| $ \begin{aligned} q_{\mathrm{FD}}(s)=& \frac{1-e^{-\gamma_{\mathrm{D}}}}{\gamma_{\mathrm{D}}} \frac{C_{\mathrm{FD}} \sqrt{c_{3}} \tanh \left(\sqrt{c_{3}}\right)}{\varPi s}-\\ & \frac{C_{\mathrm{FD}} \beta_{1}}{\varPi \sqrt{c_{3}}} \tanh \left(\sqrt{c_{3}}\right) \end{aligned} $ | (36) |
再根据摄动变换的逆变换和Sthefest数值反演进行求解。
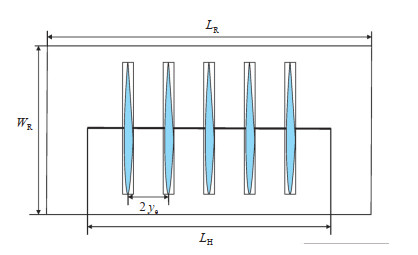
2.4 多裂缝叠加处理如图 3压裂水平井的裂缝分布所示,假设主裂缝在水平井上均匀分布,定压情况下,不同裂缝处的产量不尽相同;定产情况下,不同裂缝处的井底流压也不同。根据裂缝的形状参数(裂缝横向控制长度与垂向控制长度之比),将裂缝分为端部和内部2种情况,假设裂缝条数为N条,则有
|
下载原图 图 3 压裂水平井的裂缝分布 Fig. 3 Fracture distribution of fractured horizontal well |
内部裂缝:
| $ \delta_{\mathrm{in}}=\frac{w_{\mathrm{R}}(N-1)}{L_{\mathrm{H}}} $ | (37) |
端部裂缝:
| $ \delta_{\mathrm{out}}=\frac{w_{\mathrm{R}}}{L_{\mathrm{R}}-L_{\mathrm{H}}} $ | (38) |
主裂缝均匀分布的压裂井的无因次压力和产量表达式为
定产工作制度:
| $ p_{\mathrm{ND}}=\frac{p_{\mathrm{D}}\left(t_{\mathrm{D}}, \delta_{\mathrm{in}}\right) \times p_{\mathrm{D}}\left(t_{\mathrm{D}}, \delta_{\mathrm{out}}\right)}{p_{\mathrm{D}}\left(t_{\mathrm{D}}, \delta_{\mathrm{in}}\right)+(N-1) p_{\mathrm{D}}\left(t_{\mathrm{D}}, \delta_{\mathrm{out}}\right)} $ | (39) |
定压工作制度:
| $ q_{\mathrm{ND}}=q_{\mathrm{D}}\left(t_{\mathrm{D}}, \delta_{\mathrm{in}}\right)(N-1)+q_{\mathrm{D}}\left(t_{\mathrm{D}}, \delta_{\mathrm{out}}\right) $ | (40) |
(1)FSRV区窜流系数
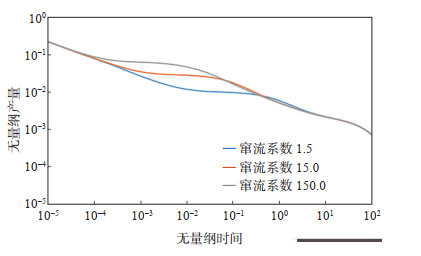
设计了FSRV区的窜流系数为1.5,15.0,150.0共3组试验。从图 4可看出,FSRV区窜流系数的大小主要影响生产的中期。油井前期产量主要依靠人工裂缝供给,无量纲产量曲线无变化,然后FSRV区和PSRV区成为主要液量供给。这是因为窜流系数越大,FSRV区的基质和裂缝的流体交换更容易,即基质向裂缝的过渡发生的越早,反之则越晚。由于补充及时使产量更早地出现平稳阶段,曲线上显示为:FSRV区窜流系数越大,则曲线平稳段出现得越早。
|
下载原图 图 4 FSRV区窜流系数对无量纲产量的影响 Fig. 4 Influence of transfer coefficient of FSRV zone on non-dimensional yield |
(2)FSRV区长度
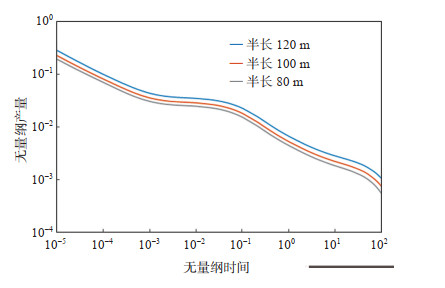
设计了FSRV区半长分别为120 m,100 m,80 m 3组试验。从图 5可看出:随着FSRV区长度的增大,SRV的作用效果越晚,非缝网改造区越少,大大减少了流体的渗流阻力,因此在曲线图上表现为:FSRV区裂缝半长越长,则无量纲产量越高,产量曲线表现为上移。
|
下载原图 图 5 FSRV区半长对无量纲产量的影响 Fig. 5 Effect of half-length of FSRV zone on non-dimensional yield |
(3)FSRV区裂缝渗透率
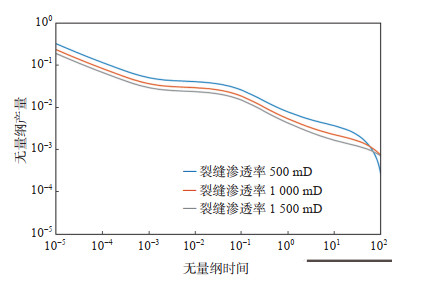
设计了FSRV区裂缝渗透率为500 mD,1 000 mD,1 500 mD共3组试验。FSRV区渗透率越大,证明人工裂缝与天然裂缝沟通越好,裂缝的导流能力越强,压裂水平井产能就越大,曲线上表现为上移。从图 6可以看出,随着生产时间的推移,缝网改造区的渗透率越大,应力敏感就越明显,后期产量下降越迅速。
|
下载原图 图 6 FSRV区裂缝渗透率对无量纲产量的影响 Fig. 6 Influence of fracture permeability of FSRV zone on dimensionless yield |
(4)FSRV宽度
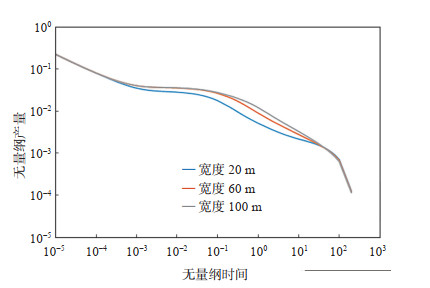
设计了FSRV区宽度为20 m,60 m,100 m共3组试验。从图 7可以看出,FSRV的宽度主要影响生产过程的中期,前期人工裂缝对产量的供给起到了主要作用,曲线无变化,中期SRV区开始供给流体,宽度越大,缝网改造效果越明显,无量纲产量平稳阶段出现的越早,平稳阶段对应产量也就越高。
|
下载原图 图 7 FSRV区宽度对无量纲产量的影响 Fig. 7 Effect of width of FSRV zone on non-dimensional yield |
(5)渗透率模量
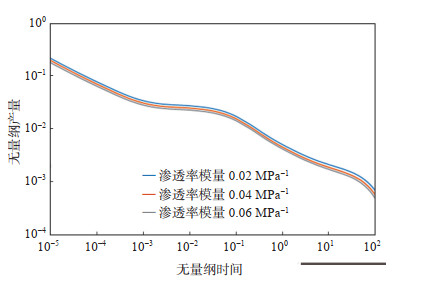
设计了FSRV区的渗透率模量为0.02 MPa-1,0.04 MPa-1,0.06 MPa-1共3组试验。从图 8可以看出,应力敏感影响所有的生产时期,虽然变化的幅度不是很明显,但随着生产时间的增加,渗透率模量越大,对无量纲产量的降低也越明显。
|
下载原图 图 8 FSRV区渗透率模量对无量纲产量的影响 Fig. 8 Influence of permeability modulus of FSRV zone on dimensionless yield |
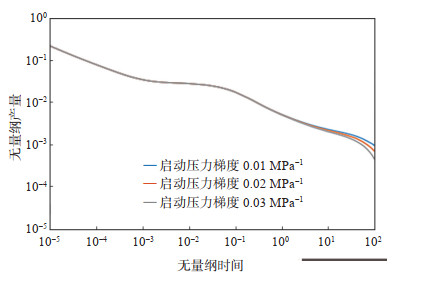
(6)启动压力梯度
设计了FSRV区的启动压力梯度为0.01 MPa-1,0.02 MPa-1,0.03 MPa-1共3组试验。从图 9可以看出,启动压力梯度主要影响生产的后期,生产初期产量由FSRV等区域供给,所以产量曲线没有变化。随着开发的进行,当压力波传到USRV区,USRV区的启动压力梯度越大,则流体流动过程中所需克服的启动压力梯度就越大,油井产量下降就越快。
|
下载原图 图 9 启动压力梯度对无量纲产量的影响 Fig. 9 Influence of starting pressure gradient on non-dimensional output |
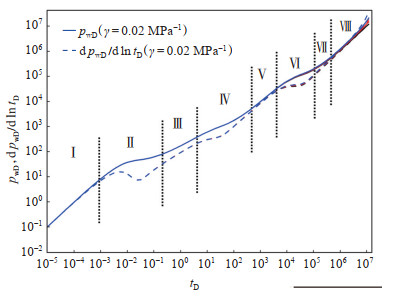
油藏的长度为1 800 m,宽度为600 m,高度为15 m。水平井长1 400 m,水力裂缝为8条,缝网改造区半长和半宽分别为100 m和20 m,水力裂缝的孔隙度、渗透率和半宽分别为20%,10 000 mD和0.003 m。2—5区裂缝的渗透率分别为1 000 mD,100 mD,10 mD,10 mD,基质渗透率分别为0.14 mD,0.14 mD,0.2 mD,0.2 mD,孔隙度分别为15%,15%,11%,11%,岩石压缩系数为0.000 23 MPa-1,流体压缩系数为0.005 MPa-1,原油黏度为1.5 mPa·s,地层体积系数为1.2,单裂缝产量为4 m3/d,启动压力梯度为0.02 MPa/m,渗透率模量为0.02 MPa-1。考虑表皮系数和无因次井筒储集系数,利用上述模型和参数计算了火山岩储集层压力曲线(图 10)。
|
下载原图 图 10 火山岩油藏压裂水平井压力动态曲线 Fig. 10 Pressure dynamic curve of fractured horizontal well in volcanic reservoir |
如图 10所示,可将流型划分为8个阶段:① HF和FSRV区的双线性流,其中压力曲线与压力导数曲线平行,斜率为1/4,当考虑表皮系数和井孔储集系数时,双线性流被掩盖;② FSRV区裂缝与基质之间的窜流,在压力导数曲线中存在凹槽;③ PSRV区的线性流动,其中压力曲线平行于压力导数曲线,斜率为1/4;④ PSRV区裂缝与基质之间的窜流,压力梯度的导数曲线变平缓(近似凹槽);⑤ USRV区的线性流动;⑥ USRV区裂缝与基质之间的窜流,压力梯度的导数曲线上升速度减慢(近似凹槽);⑦整个区域的复杂线性流动(FSRV+PSRV+USRV);⑧边界控制流。
将推导出的定产条件下的日产油量公式利用MATLAB编程,结合新疆油田准噶尔盆地火山岩油藏某井实际矿场资料,计算出解析解下的日产油量,并将其与实际生产数据进行对比。从图 11可以看出,复合流动模型的计算结果与实际产量吻合较好,证明了解析模型的准确性。

|
下载原图 图 11 复合流动模型验证 Fig. 11 Validation of composite flow model |
(1)火山岩油藏压裂水平井复合流动模型考虑了油藏内部多尺度流动,将储层细划为5个连续流动区域:USRV(未改造区)区域4和5,FSRV(完全改造区)区域2,PSRV(部分压裂改造区)区域3和HF(人工裂缝区)区域1。
(2)考虑火山岩储层中流体渗流存在启动压力梯度及应力敏感性,建立了封闭边界火山岩油藏压裂水平井数学模型,求解了偏微分方程并应用Laplace变换和Stehfest数值反演得到了定产和定压情况下封闭边界单条裂缝的井底压力和水平井产量解析解。
(3)产能影响因素敏感性分析表明,SRV区的参数(如宽度、长度、渗透率)主要影响中间流动阶段。USRV区的参数(如宽度、长度、渗透率)、非达西流动和应力敏感性主要影响后期流动阶段。此外,未改造区的的启动压力梯度、应力敏感性以及储渗方式对产量变化有重要影响。
| [1] |
伍友佳, 戴勇, 雷家华, 等. 新疆火山岩油藏开发研究. 北京: 石油工业出版社, 2013. WU Y J, DAI Y, LEI J H, et al. Xinjiang volcanic reservoir development research. Beijing: Petroleum Industry Press, 2013. |
| [2] |
邹才能, 赵文智, 贾承造, 等. 中国沉积盆地火山岩油气藏形成与分布. 石油勘探与开发, 2008, 35(3): 257-271. ZOU C L, ZHAO W Z, JIA C Z, et al. Formation and distribution of volcanic oil and gas reservoirs in Chinese sedimentary basins. Petroleum Exploration and Development, 2008, 35(3): 257-271. DOI:10.3321/j.issn:1000-0747.2008.03.001 |
| [3] |
LARSEN L, HEGRE T M. Pressure-transient behavior of horizontal wells with finite conductivity vertical fractures. SPE 22076, 1991.
|
| [4] |
GUO G, EVANS R D. A systematic methodology for produc-tion modeling of naturally fractured reservoirs intersected by horizontal wells. International Conference on Recent Advances in Horizontal Well Applications, Calgary, 1994.
|
| [5] |
郎兆新, 张丽华, 程林松. 压裂水平井产能研究. 石油大学学报(自然科学版), 1994, 18(2): 43-46. LANG Z X, ZHANG L H, CHENG L S. Study on productivity of fracturing horizontal wells. Journal of University of Petroleum, China(Natural Science Edition), 1994, 18(2): 43-46. |
| [6] |
程林松, 李春兰, 郎兆新, 等. 分支水平井产能的研究. 石油学报, 1995, 16(2): 49-55. CHENG L S, LI C L, LANG Z X, et al. Research on productivity of branch horizontal wells. Acta Petrolei Sinica, 1995, 16(2): 49-55. DOI:10.3321/j.issn:0253-2697.1995.02.011 |
| [7] |
HORNE R N, TEMENG K O. Relative productivities and pressure transient modeling of horizontal wells with multiple fractures. SPE 29891, 1995.
|
| [8] |
范子菲, 方宏长, 牛新年. 裂缝性油藏水平井稳态解产能公式研究. 石油勘探与开发, 1996, 23(3): 52-57. FANG Z F, FANG H C, NIU X N. Study on productivity formula of horizontal wells in fractured reservoirs. Petroleum Exploration and Development, 1996, 23(3): 52-57. DOI:10.3321/j.issn:1000-0747.1996.03.011 |
| [9] |
宁正福, 韩树刚, 程林松, 等. 低渗透油气藏压裂水平井产能计算方法. 石油学报, 2002, 23(2): 68-71. NING Z F, HAN S G, CHENG L S, et al. Productivity calculation method of fracturing horizontal wells in low permeability oil and gas reservoirs. Acta Petrolei Sinica, 2002, 23(2): 68-71. DOI:10.3321/j.issn:0253-2697.2002.02.015 |
| [10] |
ZERZAR D, TIAB Y B. Interpretation of multiple hydraulically fractured horizontal wells. SPE 88707, 2004.
|
| [11] |
郭肖, 伍勇. 启动压力梯度和应力敏感效应对低渗透气藏水平井产能的影响. 石油与天然气地质, 2007, 28(4): 539-543. GUO X, WU Y. Influence of start-up pressure gradient and stress sensitivity effect on horizontal well productivity in low permeability gas reservoirs. Oil and Gas Geology, 2007, 28(4): 539-543. DOI:10.3321/j.issn:0253-9985.2007.04.017 |
| [12] |
VALKO P P, AMINI S. The method of distributed volumetric sources for calculating the transient and pseudo steady state productivity of complex well fracture configurations. SPE 106279, 2007.
|
| [13] |
BELLO R O, WATTENBARGER R A. Multi-stage hydraulically fractured horizontal shale gas well rate transient analysis. SPE 126754, 2010.
|
| [14] |
WARREN J E, ROOT P J. The behavior of naturally fractured reservoirs. SPE Journal, 1963, 3(3): 245-255. |
| [15] |
BROWN M, OZKAN E, RAGHAVAN R, KAZEMI H. Practical solutions for pressure-transient responses of fractured horizontal wells in unconventional shale reservoirs. SPE 125043, 2011.
|
| [16] |
姚军, 殷修杏, 樊冬艳, 等. 低渗透油藏的压裂水平井三线性流试井模型. 油气井测试, 2011, 20(5): 1-5. YAO J, YIN X X, FAN D Y, et al. Trilinear flow test model for fracturing horizontal wells in low permeability reservoirs. Oil and Gas Well Testing, 2011, 20(5): 1-5. DOI:10.3969/j.issn.1004-4388.2011.05.001 |
| [17] |
苏玉亮, 王文东, 盛广龙. 体积压裂水平井复合流动模型. 石油学报, 2014, 35(3): 504-510. SU Y L, WANG W D, SHENG G L. Compound flow model of volumetric fracturing horizontal well. Acta Petrolei Sinica, 2014, 35(3): 504-510. |
| [18] |
潘有军, 荆文波, 徐赢, 等. 火山岩油藏水平井体积压裂产能预测研究. 岩性油气藏, 2018, 30(3): 159-164. PAN Y J, JING W B, XU Y, et al. Productivity prediction of horizontal wells by volume fracturing in volcanic reservoirs. Lithologic Reservoirs, 2018, 30(3): 159-164. |
| [19] |
苏皓, 雷征东, 张荻萩, 等. 致密油藏体积压裂水平井参数优化研究. 岩性油气藏, 2018, 30(4): 140-148. SU H, LEI Z D, ZHANG D Q, et al. Volume fracturing parameters optimization of horizontal well in tight reservoir. Lithologic Reservoirs, 2018, 30(4): 140-148. |
| [20] |
宋宣毅, 刘月田, 马晶, 等. 基于灰狼算法优化的支持向量机产能预测. 岩性油气藏, 2020, 32(2): 134-140. SONG X Y, LIU Y T, MA J, et al. Productivity forecast based on support vector machine optimized by grey wolf optimizer. Lithologic Reservoirs, 2020, 32(2): 134-140. |
| [21] |
KIKANI J, PEDROSA JR O A. Perturbation analysis of stresssensitive reservoirs. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1992, 29(3): A160. |
 2021, Vol. 33
2021, Vol. 33




