2. 中国石化石油勘探开发研究院, 北京 100083;
3. 中国石化华北油气分公司 采气一厂, 郑州 450006
2. Sinopec Research Institute of Petroleum Exploration and Production, Beijing 100083, China;
3. No. 1 Gas Production Plant, Sinopec North China Oil and Gas Company, Zhengzhou 450006, China
现代试井解释分析方法广泛应用于获取储层物性参数、探测储层边界信息[1]。Lefkovits等[2] 1961年首次分析合采井的压力动态特征,奠定多层合采储层试井方法的基础。20世纪90年代,我国徐献芝[3]、张望明[4]、李顺初[5]等众多学者最先发展多层合采储层试井分析理论和方法。高承泰[6]、孙贺东等[7-8]建立存在层间越流的多层合采储层试井模型,发展多层合采储层的试井方法。
随着油气勘探力度的增大以及钻采工艺技术的提高,试井分析中最常用的无限大、定压、封闭边界已不能满足油气藏精细化描述的需求,复杂结构井[9]以及复杂边界类储层[10]的试井模型已经引起大家的高度重视。何应付等[11]采用边界数值试井方法分析单层圆形储层“一半定压一半封闭”混合边界案例,结果表明混合边界能明显延迟压力导数出现下掉时间。郭显赋等[12]建立复杂外边界裂缝性低渗透油藏数值试井模型,认为压力导数出现下掉的时间随定压边界条数增加而提前。Shi等[13]建立封闭边界距离不等的n层合采储层试井模型,以抛物线型的外凸封闭边界来分析边界的形状、类型对储层渗流和压力响应的影响。郑荣臣等[14]基于椭圆流建立多层酸压改造井的压力响应模型,分析双层复合模型的敏感性参数,但仅绘制上下层边界类型(无限大、定压、封闭)不同条件下的压力响应曲线,未系统的讨论与分析上下层边界组合类型。
近年来,中石化在川西坳陷勘探取得重大突破[15-19],显示川西地区龙门山前构造雷口坡组、须家河组储层具有明显的多层叠置、构造空间结构复杂等特征[20-24]。一方面,现有的商业试井软件虽然已有多层不同一边界的分析模型,但实际油气田现场分析者仍多应用单层单类边界模型分析,往往出现边界阶段无法拟合、解释参数异常的现象。另一方面,虽然已有人研究多层混合边界模型,但未见系统分析多层混合边界类型对压力响应影响的报道,也没有混合边界下试井诊断曲线特征的探索。为了彰显单层单类边界与多层混合边界模型压力响应的差异性,探究纵纵向混合边界对压力响应特征的影响规律,本文建立纵向组合边界储层渗流模型。以双层合采储层为例,绘制纵向任意边界(无限大、定压、封闭)组合下的压力响应典型曲线,并划分流动阶段,系统讨论纵向组合边界的组合模式、不同边界占比对储层渗流以及压力响应特征的影响规律。
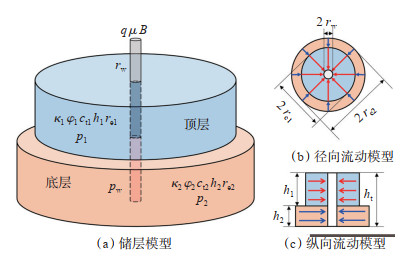
1 模型建立 1.1 物理模型考虑储层中心为一口合采井,存在纵向组合边界合采储层的物理模型[图 1(a)]基本假设条件如下:
|
下载原图 图 1 纵向组合边界储层物理模型 q为产量,m3/d;μ为黏度,mPa·s;B为等温体积系数;rw为井筒半径,m;k为渗透率,mD;φ为孔隙度;ct为综合压缩系数,MPa-1;h为厚度,m;re为边界距离,m;p为压力,MPa;pw为井底压力,MPa;下标1表示顶层;下标2表示底层;Ω表示恒压边界;Θ表示封闭边界;∞表示无限大边界 Fig. 1 Physical model of commingled reservoir with vertical combined boundary |
(1)开井生产前,储层充满单相微可压缩流体,顶层压力和底层压力均等于储层原始地层压力。
(2)生产过程中,储层流体黏度不变,生产井的产量为定值。
(3)顶层和底层具有不同的渗透率、孔隙度、综合压缩系数、厚度、边界距离和边界类型。
(4)顶、底层储层流体仅通过所在层径向流入井筒[图 1(b)];各层间不存在层间窜流[图 1(c)]。
(5)考虑井筒储集和近井储层表皮的影响。
(6)忽略储层温度变化和重力效应对流动的影响。
1.2 数学模型定义无量纲径向距离rD = r/rw,无量纲时间tD = 0.003 6(k1h1+ k2h2)t/[(φ1 ct1 h1+ φ2 ct2 h2)μrw2],无量纲井储系数CD = 0.1592 C/[(φ1 ct1 h1+φ2 ct2 h2)rw2],顶层流度比κ1 = k1 h1/(k1 h1+ k2 h2),底层流度比κ1 = k2h2/(k1h1+ k2h2),顶层储容比ω1 = φ1ct1h1/(φ1 ct1h1+ φ2 ct2h2),底层储容比ω2 = φ2 ct2h2/(φ1 ct1h1+φ2 ct2h2),顶层无量纲压力p1D = 0.542 8(k1h1+k2 h2)(pr-p1)/(qμB),底层无量纲压力p2D = 0.542 8(k1h1+k2h2)(pr-p2)/(qμ B)。其中:t为生产时间,h;C为井储系数,m3/MPa;pr为原始储层压力,MPa。
考虑井筒储集、近井表皮效应的单相微可压缩流体在多层合采储层渗流方程为[25]
| $ \frac{1}{{{r_{\rm{D}}}}}\frac{\partial }{{\partial {r_{\rm{D}}}}}({r_{\rm{D}}}\frac{{{\partial ^2}{P_{j{\rm{D}}}}}}{{\partial {r_{\rm{D}}}}}) = \frac{{{\omega _j}}}{{{C_{\rm{D}}}{e^{2S}}{k_j}}}\frac{{\partial {P_{j{\rm{D}}}}}}{{\partial {t_{\rm{D}}}}}, j = \{ 1, 2\} $ | (1) |
其中:S为表皮系数。
当储层流体为气体时,采用拟时间[26]t = μ0cg0· ∫[1(/ μ cg)]d t和拟压力[27]m = Z0 μ/p0∫[p/(Zμ)]d p完成无量纲油气渗流方程的统一。其中,Z为气体压缩因子;下标0表示参考点。下文不在区分油、气,无量纲渗流方程中统一用压力p和时间t表示。
对无量纲渗流方程(1)进行Laplace变换,无量纲渗流数学模型在Laplace空间下为
| $ \frac{1}{{{r_{\rm{D}}}}}\frac{\partial }{{\partial {r_{\rm{D}}}}}[{r_{\rm{D}}}\frac{{{\partial ^2}{{\overline P }_{j{\rm{D}}}}({r_{\rm{D}}}, u)}}{{\partial {r_{\rm{D}}}}}] = {\sigma _j}{\overline P _{j{\rm{D}}}}({r_{\rm{D}}}, u), j = \{ 1, 2\} $ | (2) |
式中:u为实空间无量纲时间tD变换后的Laplace空间变量;σj=[uωj/(CD e2 Sκj)]1/2。
初始条件下,各层压力均等于储层原始地层压力,初始条件在Laplace空间下的无量纲形式为
| $ {\overline P _{1{\rm{D}}}}({r_{\rm{D}}}, 0) = {\overline P _{2{\rm{D}}}}({r_{\rm{D}}}, 0) = 0 $ | (3) |
生产井井底产量等于各层流量之和,井筒流量条件在Laplace空间下的无量纲形式为
| $ [{r_{{\rm{wD}}}}{k_1}\frac{{\partial {{\overline P }_{1{\rm{D}}}}({r_{{\rm{wD}}}}, u)}}{{\partial {r_{\rm{D}}}}}{\rm{ + }}{r_{{\rm{wD}}}}{k_2}\frac{{\partial {{\overline P }_{2{\rm{D}}}}({r_{{\rm{wD}}}}, u)}}{{\partial {r_{\rm{D}}}}}] = - \frac{1}{u} $ | (4) |
各层压力在井筒位置相等,且等于井底压力,井筒压力条件在在Laplace空间下的无量纲形式为
| $ {\overline P _{{\rm{wD}}}} = {\overline P _{1{\rm{D}}}}({r_{{\rm{wD}}}}, u) = {\overline P _{2{\rm{D}}}}({r_{{\rm{wD}}}}, u) $ | (5) |
储层边界为定压边界时,边界处的压力等于储层初始地层压力,定压边界的压力条件在Laplace空间下的无量纲形式为
| $ \begin{array}{*{20}{l}} {{{\overline P }_{j{\rm{D}}}}({r_{{\rm{eD}}}}, u) = 0, j = \{ 1, {\rm{ }}2\} } \end{array} $ | (6) |
储层无穷大边界的压力条件在Laplace空间下的无量纲形式为
| $ \begin{array}{*{20}{l}} {{{\overline P }_{j{\rm{D}}}}(\infty , u) = 0, j = \{ 1, {\rm{ }}2\} } \end{array} $ | (7) |
储层边界为封闭边界时,边界处无流体流动,封闭边界的流量条件在Laplace空间下的无量纲形式为
| $ \frac{{\partial {{\overline P }_{j{\rm{D}}}}({r_{{\rm{eD}}}}, u)}}{{\partial {r_{\rm{D}}}}} = 0, j = \{ 1, {\rm{ }}2\} $ | (8) |
方程(2)属于Bessel类方程,其解可用Bessel函数表示为[28-29]
| $ {\overline P _{j{\rm{D}}}}({r_{\rm{D}}}, u) = {A_j}{I_0}({\sigma _j}{r_{\rm{D}}}) + {B_j}{K_0}({\sigma _j}{r_{\rm{D}}}), j = \{ 1, {\rm{ }}2\} $ | (9) |
式中:Aj,Bj为待求系数;I0为0阶第1类修正Bessel函数;K0为0阶第2类修正Bessel函数。式(9)的导数为储层压力在径向上的压力梯度,其计算式为
| $ \frac{{\partial {{\overline P }_{j{\rm{D}}}}}}{{\partial {r_{\rm{D}}}}}{\rm{ = }}{A_j}{\sigma _j}{I_j}({\sigma _j}{r_{\rm{D}}}) - {B_j}{\sigma _j}{K_j}({\sigma _j}{r_{\rm{D}}}), j = \left\{ {1, 2} \right\} $ | (10) |
将压力解(9)及压力梯度(10)代入边界条件(3)—(8),得到关于系数Aj,Bj的线性方程组
| $ \left[ {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}&{{a_{13}}}&{{a_{14}}}\\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}}&{{a_{24}}}\\ {{a_{31}}}&{{a_{32}}}&0&0\\ 0&0&{{a_{43}}}&{{a_{44}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{A_1}}\\ {{B_1}}\\ {{A_2}}\\ {{B_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\underline { - 1} }\\ u\\ 0\\ 0\\ 0 \end{array}} \right] $ | (11) |
式中:a11 = κ1 σ1 I1(rwD σ1);a12 = -κ1 σ1 K1(rwD σ1);a13 =κ2 σ2 I1(rwD σ2);a14 = -κ2 σ2 K1(rwD σ2);a21 = I0(rwD σ1);a22 = K0(rwD σ1);a23 = -I0(rwD σ2);a24 = -K0(rwD σ2);I1为1阶第1类修正Bessel函数;K1为1阶第2类修正Bessel函数;系数a31,a32,a42,a44见表 1。
|
|
下载CSV 表 1 不同边界组合下a31,a32,a42,a44值 Table 1 Values of a 31, a32, a42, a44 under different boundary combinations |
利用克莱姆法则求解线性方程组(11),求得未知系数A1,B1,代入顶层的压力解方程中得到Laplace空间下无量纲井底压力解:
| $ {\overline P _{{\rm{wD}}}} = {\overline P _{1{\rm{D}}}}({r_{{\rm{wD}}}}, u) $ | (12) |
通过Stehfest数值反演算法[30]对Laplace空间无量纲井底压力解进行反演,能够得到实空间无量纲井底压力解。
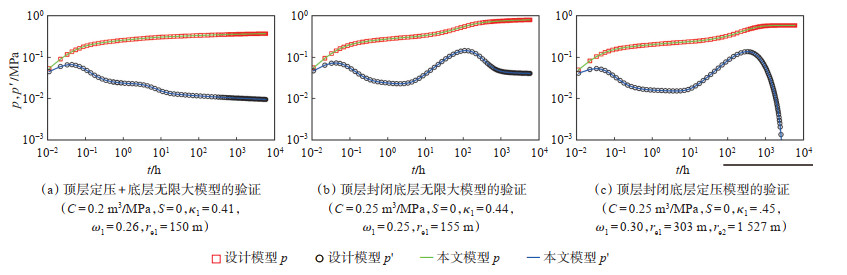
2.2 模型验证建立生产井位于圆形储层中心的2层油藏数值模型模型,初始压力为34.48 MPa,顶部深度为1 828.8 m,顶层厚度为30.48 m,孔隙度为0.1,渗透率为20 mD,底层厚度为15.24 m、孔隙度为0.5、渗透率为50 mD,储层顶、底层边界类型和距离如表 2所示,岩石和流体的其它参数使用软件默认值,生产井以31.78 m3/d的产量生产5 000 h后关井6 000 h。由于KAPPA软件设计模型所产生压降数据与压恢数据相差甚微(测试1 000 h内绝对误差远小于6.89×10-3 MPa,相对误差远小于1%;测试5 000 h内绝对误差远小于2.76×10-2 MPa,相对误差远小于3.5%),采用商业数值模拟软件设计模型中物理参数进行压恢数据拟合(图 2),验证本文解析模型的可靠性。
|
|
下载CSV 表 2 本文模型与验证模型的参数取值 Table 2 Parameters of this model and validated model |
|
下载原图 图 2 3种模型的验证结果 Fig. 2 Verified results of three models |
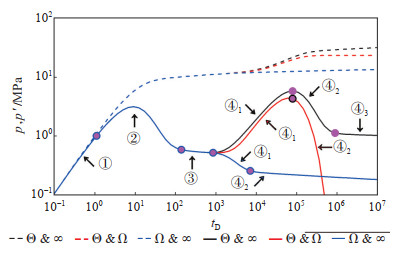
表 3汇总并比较了不同纵向组合边界下储层压力响应行为下的流动阶段特征。在图 3“封闭+ 无限大层”(Θ+∞)储层:早期压力波遇到封闭边界,出现压力导数递增的封闭边界流;中期压力波绕过封闭层向无限大层继续传播,压力导数递减;后期压力波在无限大层持续传播,出现压力导数稳定的拟径向流。在图 3“定压+无限大”(Ω + ∞)储层:早期压力波遇到定压边界,出现压力导数递减的定压边界流;后期压力波穿过定压层在无限大层继续传播,出现压力导数直线递减的拟定压边界流。在图 3“封闭+ 定压”(Θ + Ω)储层:早期出现压力波遇到封闭边界并穿透定压边界的封闭边界流,后期出现压力波绕过封闭边界穿透定压边界的定压边界流。图 3表明纵向组合边界储层的压力响应曲线形态和对应的压力及压力导数特征值能够判断边界组合类型。
|
|
下载CSV 表 3 不同组合边界储层流动阶段及压力特征 Table 3 Flow regimes and pressure response under different boundary combinations |
|
下载原图 图 3 不同纵向组合边界下储层压力响应典型曲线 CD = 10,S = 3,κ1 = κ2 = ω1 = ω2 = 0.5,re1 D = re2 D = 5 000 Fig. 3 Typical curves of pressure response under different boundary combinations |
当顶层和底层的厚度相同时,流动系数比表示流体在顶层流动占整个储层流动的比例;当顶层和底层渗透率相同时,流动系数表示顶层占整个储层的厚度比例。因此,采用顶层流动系数比κ1表征顶层储层边界的占比。κ1越大,表示顶层在整个储层的流动占比越高,顶层在整个储层的边界占比越大。
(1)无限大+ 封闭边界(∞+ Θ)
图 4(a)显示了“无限大+ 封闭(∞+ Θ)”储层中无限大边界占比κ1对压力响应的影响;无限大顶层占比κ1越大,边界流早期的压力导数递增越趋向边界流后期的压力导数稳定,且拟径向流阶段的压力导数l随着无限大边界占比κ1增大而变小。图 4(b)进一步揭示了边界流后期拟径向流压力导数稳定值l和无限大边界占比κ1之间的关系:l·κ1 = 0.5。其中,0.5为无限大储层径向流对应的压力导数值l0。

|
下载原图 图 4 “无限大+封闭”储层中无限大边界占比对压力响应的影响(CD = 10,S = 3,ω1 = ω2 = 0.5,reD = 5 000)(a)和拟径向流压力导数和无限大边界占比的关系(b) Fig. 4 Effects of infinite boundary on pressure response in infinite & closed boundary model(a)relationship between permeability ratio of infinite boundary and pressure derivative in radial flow regime(b) |
图 5显示了“无限大+ 封闭”储层的“等效复合储层”现象:如果将封闭底层边界所在位置reD当做复合半径rcD,无限大边界占比κ当做外区对内区的流度比M,则“无限大+封闭”储层[图 5(a)]与物性变差的两区径向复合储层[图 5(b)]具有相似的压力响应特征:压力导数在第一径向流、第二径向流阶相同[图 5(c)]。若强行使用复合模型去拟合“无限大+ 封闭”模型的压力响应数据,将得到异常高的储容系出比、异常低的复合半径和偏高的表皮系数,如表 4所示。因此需要格外小心地从地质特征和流态判断方面去区别两者,避免仅依据试井曲线形态而误选模型。

|
下载原图 图 5 “无限大+ 封闭”储层与等效复合储层压力响应曲线 Fig. 5 Relationship of pressure response curve between infinite & closed boundary model and radial composite model |
(2)无限大+ 定压边界(∞+ Ω)
[图 6(a)]显示了“无限大+定压(∞+ Ω)”储层中定压边界占比κ2对压力响应的影响:定压边界占比κ2越大,边界流早期压力导数递减越快,且边界流后期拟定压边界流压力导数直线递减斜率m越大。[图 6(b)]进一步揭示了拟定压边界流压力导数斜率m和定压边界占比κ2之间的线性正相关关系:m = 0.068 3 κ2,系数0.068 3与定压边界的距离无关。

|
下载原图 图 6 “无限大+定压”储层中定压边界占比对压力响应的影响(CD = 10,S = 3,ω1 = ω2 = 0.5,reD= 5 000)(a)和储层拟定压边界流压力导数斜率与定压边界占比的关系(b) Fig. 6 Effects of constant-pressure boundary on pressure response in infinite & constant-pressure boundary model(a) and relationship between permeability ratio of constant-pressure boundary and pressure derivative slope in pseudo constant-pressure flow regime(b) |
(3)定压+ 封闭边界(Ω+Θ)
[图 7(a)]显示了“定压+封闭(Ω + Θ)”储层中定压边界占κ1比对压力响应的影响。当κ1 < 0.5时封闭底层为主导层,边界流早期出现主导层的封闭边界流、后期出现非主导层的定压边界流;当κ1 > 0.5时定压顶层为主导层,边界流早期为主导层的定压边界流、中期出现非主导层的封闭边界流。后期又显示主导层的定压边界流。需要注意此处压力导数出现的“凹子”并非是双重介质窜流引起的。图[图 7(b)]揭示了边界流后期压力稳定值L与定压边界占比κ1之间的定量关系:L·κ1 = 11.518。其中,11.518是边界距离为5 000的单层定压边界模型中压力稳定值L0(κ1= 1,re1D= 5 000)。

|
下载原图 图 7 “定压+封闭”储层中定压边界占比对压力响应的影响(CD=10,S=3,ω1=ω2=0.5,re1D=re2D=5 000)和(a)储层压力稳定值与定压边界占比的关系(b) Fig. 7 Effects of constant-pressure boundary on pressure response in constant-pressure & closed boundary model(a) and relationship between permeability ratio of constant-pressure boundary and pressure constant value(b) |
川西XC气田须家河组发育东北—西南走向的逆断层[图 8(a)],且断层附近的储层具有良好的油气储集性[31-32]。储层构造剖面[图 8(b)]显示储层具有明显的分层特征,裂缝类型多,储层具有很强的非均质性[33-34]。选取试井资料质量较好的5口典型井(X10,X3,X853,X8,X5)进行分析,其对应的储层参数、流体参数和生产参数见表 5。

|
下载原图 图 8 川西XC气田须家河组综合图 Fig. 8 Comprehensive map of Xujiahe Formation in XC gas field, western Sichuan Basin |
|
|
下载CSV 表 5 川西XC气田典型井的须家河组储层及流体参数 Table 5 Reservoir and fluid parameters of Xujiahe Formation in typical wells in XC gas field, western Sichuan Basin |
XC气田储层上部为气层,下部为上倾尖灭的气水同层。X10井上部以Ⅱ类储层为主,远井区域的X301附近发育裂缝,因此,选择上部封闭、下部无限大的边界模型解释。参考邻井X301构造,X3井近井区域为裂缝沟通较好的Ⅰ类储层,由于断层和高角裂缝沟通底部气水层,下部气水层对上部气层具有良好的能量补充,因此,选择上部定压边界、下部无限大的边界模型解释。X853,X8,X5所处构造特征具有相似性:都位于一对逆断层所加持区域的边缘,上部储层发育裂缝,物性好,因此选择上部定压、下部封闭的边界模型解释。5口典型井的解释参数如表 6所列,拟合效果如图 9所示。
|
|
下载CSV 表 6 川西XC气田典型井储层参数解释结果 Table 6 Interpreted reservoir parameters of Xujiahe Formation in typical wells in XC gas field, western Sichuan Basin |

|
下载原图 图 9 川西XC气田典型井数据拟合结果 Fig. 9 Matching curves of typical wells in XC gas field, western Sichuan Basin |
选取的模型能够合理解释5口典型井对应的构造特征,佐证了底部气水上侵成为驱动能量的可能性。根据从东部到西部5口典型井的解释结果,大致可以圈定一个由于断层和高角裂缝沟通底部气水层而产生的压力驱动区域范围[图 8(b)]。位于圈定压力驱动区域范围内部的气井,要合理控制采气速度,稳定驱动边界的推进速度、防止出现暴性水侵。圈定压力驱动能量区域范围内部的生产气井,需要合理地控制目前生产气井的采气速度,以期来稳定驱动能量水体边界的推进速度,防止底部能量水体沿着断裂伴生裂缝入侵而出现的暴性水侵、水淹等现象。
5 结论(1)“封闭+ 无限大”边界模型早期为压力导数递增的封闭边界流、后期为压力导数稳定的拟径向流;拟径向流阶段压力导数值与封闭边界占比的乘积为定值,且定值为单层无限大储层径向流阶段的压力导数值。
(2)“定压+ 无限大”边界模型早期为压力导数下吊的定压边界流、后期为压力导数直线递减的拟定压边界流;拟定压边界流阶段压力导数递减斜率与定压边界占比成线性正相关。
(3)“定压+封闭”边界早期为主导层的边界流、后期为压力导数下吊的定压边界流;边界流后期定压边界流阶段压力值与定压边界占比的乘积为定值,且定值为单层定压储层边界流阶段的压力值。
(4)实例应用表明压力响应曲线形态可直接定性诊断纵向组合边界的类型,边界流阶段的压力响应特征值可快速确定纵向边界的占比;当储层压力响应出现物性变差的径向复合储层以及双重介质储层特征时,应结合实际储层地质信息谨慎选择解释模型。
| [1] |
SUN B, SHI W Y, Zhang R, et al. Transient behavior of vertical commingled well in vertical non-uniform boundary Radii reservoir. Energies, 2020, 13(9): 2305. DOI:10.3390/en13092305 |
| [2] |
LEFKOVITS H C, HAZEBROEK P, ALLEN E E, et al. A study of the behavior of bounded reservoirs composed of stratified layers. SPE Journal, 1961, 1(1): 43-58. |
| [3] |
徐献芝, 况国华, 陈峰磊, 等. 多层合采试井分析方法. 石油学报, 1999, 20(5): 43-47. XU X Z, KUANG G H, CHEN F L, et al. Multilayer commingled well test analysis method. Acta Petrolei Sinica, 1999, 20(5): 43-47. |
| [4] |
张望明, 韩大匡, 连淇祥, 等. 多层油藏试井分析. 石油勘探与开发, 2001, 38(3): 63-66. ZHANG W M, HAN D K, LIAN Q X, et al. Multilayer reservoir well test analysis. Petroleum Exploration and Development, 2001, 38(3): 63-66. DOI:10.3321/j.issn:1000-0747.2001.03.018 |
| [5] |
李顺初, 张普斋, 黄炳光. 多层油藏压力分布的一般解. 西南石油学院学报, 2002, 24(4): 28-29. LI S C, ZHANG P Z, HUANG B G, et al. General solution of pressure distribution in multilayer reservoir. Journal of Southwest Petroleum University(Science & Technology Edition), 2002, 24(4): 28-29. DOI:10.3863/j.issn.1674-5086.2002.04.008 |
| [6] |
高承泰, 孙贺东. 多层越流油气藏试井分析方法. 北京: 石油工业出版社, 2018. GAO C T, SUN H D. Well test analysis method for multilayer crossflow oil and gas reservoir. Beijing: Petroleum Industry Press, 2018. |
| [7] |
孙贺东, 高承泰, 周芳德. 具有越流的多层气藏的压力曲线特征. 西安石油学院学报(自然科学版), 2001, 16(6): 25-29. SUN H D, GAO C T, ZHOU F D. Characteristics of pressure curve of multilayer gas reservoir with overflow. Journal of Xi'an Shiyou University(Natural Science Edition), 2001, 16(6): 25-29. DOI:10.3969/j.issn.1673-064X.2001.06.008 |
| [8] |
孙贺东, 周芳德, 高承泰, 等. 三层越流油藏井底压力的精确解. 石油钻采工艺, 2003, 25(3): 41-44. SUN H D, ZHOU D F, GAO C T. Exact solution and typical curve of three layers crossflow reservoir. Oil Drilling & Production Technology, 2003, 25(3): 41-44. DOI:10.3969/j.issn.1000-7393.2003.03.010 |
| [9] |
程时清. 复杂结构井试井分析理论与方法. 北京: 科学出版社, 2018. CHENG S Q. Theory and method of well test analysis for complex structure wells. Beijing: Science Press, 2018. |
| [10] |
贾英兰. 多层油气藏复杂渗流理论与试井分析方法研究. 成都: 西南石油大学, 2014. JIA Y L. Study on complex seepage theory and well test analysis method for multilayer oil and gas reservoirs. Chengdu: Southwest Petroleum University, 2014. |
| [11] |
何应付, 尹洪军, 林木, 等. 任意形状复合油藏压力动态的边界元分析. 水动力学研究与进展(A辑), 2006, 21(6): 700-705. HE Y F, YIN H J, LIN M, et al. Pressure transient analysis of composite reservoir using the boundary element method. Chinese Journal of Hydrodynamics, 2006, 21(6): 700-705. |
| [12] |
郭显赋, 梁景伟, 孙德巨, 等. 复杂边界裂缝性低渗油藏有限元试井. 断块油气田, 2011, 18(1): 87-90. GUO X B, LIANG J W, SUN D J, et al. Finite-element well testing of low-permeability fractured reservoir with complex outer-boundary. Fault-Block Oil & Gas Field, 2011, 18(1): 87-90. |
| [13] |
SHI W Y, CHENG S Q, MENG L X, et al. Pressure transient behavior of layered commingled reservoir with vertical inhomogeneous closed boundary. Journal of Petroleum Science and Engineering, 2020, 189(6): 106995. |
| [14] |
郑荣臣, 严谨, 张郁哲, 等. 多层压裂改造气井椭圆渗流压力动态特征. 断块油气田, 2020, 27(2): 207-212. ZHENG R C, YAN J, ZHANG Y Z, et al. Pressure transient behavior of multi-layer fracturing gas wells with elliptical flow. Fault-Block Oil and Gas Field, 2020, 27(2): 207-212. |
| [15] |
赵向原, 胡向阳, 肖开华, 等. 川西彭州地区雷口坡组碳酸盐岩储层裂缝特征及主控因素. 石油与天然气地质, 2018, 39(1): 30-39. ZHAO X Y, HU X Y, XIAO K H, et al. Characteristics and major control factors of natural fractures in carbonate reservoirs of Leikoupo Formation in Pengzhou area, western Sichuan Basin. Oil & Gas Geology, 2018, 39(1): 30-39. |
| [16] |
王志宏, 郝翠果, 李建明, 等. 川西前陆盆地超压分布及成因机制. 岩性油气藏, 2019, 31(6): 1-8. WANG Z H, HAO C G, LI J M, et al. Distribution and genetic mechanism of overpressure in western Sichuan foreland basin. Lithologic Reservoirs, 2019, 31(6): 1-8. |
| [17] |
王登, 余江浩, 赵雪松, 等. 四川盆地石柱地区自流井组页岩气成藏条件与勘探前景. 岩性油气藏, 2020, 32(1): 27-35. WANG D, YU J H, ZHAO X S, et al. Accumulation conditions and exploration potential of shale gas of Ziliujing Formation in Shizhu area. Lithologic Reservoirs, 2020, 32(1): 27-35. |
| [18] |
史文洋, 姚约东, 程时清, 等. 川西潮坪相裂缝型碳酸盐岩分层酸压井压力动态分析. 岩性油气藏, 2020, 32(1): 152-160. SHI W Y, YAO Y D, CHENG S Q, et al. Pressure transient analysis for separate-layer acid fracturing well of tidal flat fractured carbonate reservoirs in western Sichuan Basin. Lithologic Reservoirs, 2020, 32(1): 152-160. |
| [19] |
罗志锋, 黄静云, 何天舒, 等. 碳酸盐岩储层酸压裂缝高度延伸规律: 以川西栖霞组为例. 岩性油气藏, 2020, 32(2): 169-176. LUO Z F, HUANG J Y, HE T S, et al. Extending regularity of fracture height by acid fracturing in carbonate reservoir: A case study of Qixia Formation in western Sichuan. Lithologic Reservoirs, 2020, 32(2): 169-176. |
| [20] |
王鹏, 沈忠民, 何崇康, 等. 川南地区须家河组天然气地球化学特征及成藏过程. 岩性油气藏, 2017, 29(5): 19-27. WANG P, SHEN Z M, HE C K, et al. Geochemical characteristics and accumulation process of natural gas of Xujiahe Formation in southern Sichuan Basin. Lithologic Reservoirs, 2017, 29(5): 19-27. |
| [21] |
李新豫, 张静, 包世海, 等. 川中地区须二段气藏地震预测陷阱分析及对策: 以龙女寺区块为例. 岩性油气藏, 2019, 31(6): 1-8. LI X Y, ZHANG J, BA S H, et al. Analysis and countermeasures of seismic prediction traps for Xujiahe gas reservoir in central Sichuan Basin: A case study from Longnyusi block. Lithologic Reservoirs, 2019, 31(6): 1-8. |
| [22] |
韩波, 何治亮, 任娜娜, 等. 四川盆地东缘龙王庙组碳酸盐岩储层特征及主控因素. 岩性油气藏, 2018, 30(1): 75-85. HAN B, HE Z L, REN N N, et al. Characteristics and main controlling factors of carbonate reservoirs of Longwangmiao Formation in eastern Sichuan Basin. Lithologic Reservoirs, 2018, 30(1): 75-85. |
| [23] |
陈志强, 吴思源, 白蓉, 等. 基于流动单元的致密砂岩气储层渗透率测井评价: 以川中广安地区须家河组为例. 岩性油气藏, 2017, 29(6): 76-83. CHEN Z Q, WU S Y, BAI R, et al. Logging evaluation for permeability of tight sandstone gas reservoirs based on flow unit classification: A case from Xujiahe Formation in Guang'an area, central Sichuan Basin. Lithologic Reservoirs, 2017, 29(6): 76-83. |
| [24] |
王睿婧, 刘树根, 张贵生, 等. 川西坳陷孝泉-新场-合兴场地区须二段天然气气源判定及成藏分析. 岩性油气藏, 2011, 23(4): 100-105. WANG R J, LIU S G, ZHANG G S, et al. Judgement of natural gas resource and accumulation analysis of the second member of Xujiahe Formation in Xiaoquan-Xinchang-Hexingchang area of West Sichuan depression. Lithologic Reservoirs, 2011, 23(4): 100-105. |
| [25] |
BOURDET D. Well test analysis: The use of advanced interpretation models. Elsevier Science, 2020. |
| [26] |
AGARWAl R G. Real gas pseudo-time: A new function for pressure buildup analysis of MHF gas wells. SPE 8279, 1979. |
| [27] |
AL HUSSAINY R, RAMEY H J, CRAWFORD P B. The flow of real gases through porous media. SPE Journal, 1966, 18(5): 624-6361. |
| [28] |
A F VAN EVERDINGEN. The skin effect and its influence on the productive capacity of a well. Journal Petroleum Technology, 1943, 5(6): 171-176. |
| [29] |
A F VAN EVERDINGEN, HURST W. The application of the Laplace transformation to flow problems in reservoirs. Pet. Technol, 1949, 1(12): 305-324. |
| [30] |
赖锦, 王贵文. 川中蓬莱地区须二段气藏特征及有利含气区预测. 岩性油气藏, 2012, 24(5): 43-49. LAI J, WANG G W. Gas reservoir characteristics of the second member of Xujiahe Formation and prediction of favorable gas bearing zones in Penglai area, central Sichuan Basin. Lithologic Reservoirs, 2012, 24(5): 43-49. |
| [31] |
唐群英, 尹太举, 路遥, 等. 川东北普光地区须家河组裂缝特征描述. 岩性油气藏, 2012, 24(2): 42-47. TANG Q Y, YIN T J, LU Y, et al. Fracture features description of Xujiahe Formation in Puguang area, northeastern Sichuan Basin. Lithologic Reservoirs, 2012, 24(2): 42-47. |
| [32] |
徐樟有, 宋丽, 吴欣松, 等. 川中地区上三叠统须家河组典型气藏解剖与天然气成藏主控因素分析. 岩性油气藏, 2009, 21(2): 7-11. XU Z Y, SONG L, WU X S, et al. Typical gas reservoirs and main controlling factors of reservoir-forming of Upper Triassic Xujiahe Formation in central Sichuan Basin. Lithologic Reservoirs, 2009, 21(2): 7-11. |
 2021, Vol. 33
2021, Vol. 33




