地震波速度是地震勘探中的一个重要参数,在地震数据处理和资料解释过程中起着不可替代的作用。速度资料是岩性、构造以及油藏描述中的重要信息之一,其认识程度直接影响了地震勘探的各个环节。只有获取精确的速度参数,才能真实反映地下空间结构特征,并准确定位油气圈闭的空间位置和展布特征[1]。在地震资料解释中,时深转换是将地震解释成果从时间域向深度域转换的一个重要桥梁[2]。地球物理中速度名词很多,包括层速度、均方根速度、叠加速度、平均速度、偏移速度等,都有着不同的用途和适用范围[3],有的仅在理论分析中用到,有的是地震资料处理中的专用参数,而地层平均速度常用来进行时深转换,想要求取精确的平均速度并不容易。针对不同地质条件下的时深转换,前人已经做了大量的探索与研究[4-7],通过构造区的经验公式、叠加剖面的叠加速度、测井速度、速度谱及井-震标定速度等方式[8-11]进行时深转换,取得了较好的应用效果。随着勘探需求的不断提高,尤其是对于构造缓且速度横向变化大的地区,常规方法已经不能满足落实其构造特征的需求,须要求取精度更高的平均速度参数。
渤海A油田位于石臼坨凸起中段缓坡带,在古隆起背景上发育多个新近系断鼻、断块型构造圈闭,单个圈闭面积较小、幅度较低,主要目的层为新近系D层,埋藏深度为1 200~1 600 m,地层结构简单,多为砂泥互层,纵向上分为多个油组,其构造特征表现为幅度平缓,为10~30 m,属于典型的低幅度构造油气藏,储层为三角洲前缘沉积。A油田已钻多口探井,在D层段揭示了良好的油气发现。A油田构造平缓,其真实的构造特征对速度横向变化敏感,因此须选取适合的速度分析方法,真实反映构造特征。本文结合渤海A油田的地质特点,在进行地层平均速度公式推导的基础上,通过分析影响研究层平均速度的敏感因素,求取由含气比、含油比和砂地比组成的多元线性拟合公式,并结合已知钻井信息通过最小二乘法求解出平均速度的表达式,以期能够反映A油田的地下构造特征,指导油田精细勘探开发。
1 研究层段的地层平均深度分析本文所述的平均速度并不是严格意义的从基准面到目标层的速度,而是特指某一研究层内的地层平均速度。结合渤海A油田已钻井信息和地震相特征分析,研究层段新近系D层之上的地层沉积稳定,厚度相当,无异常的特殊岩性,地层平均速度横向变化较小。图 1为A油田D层段Ⅱ油组的地层平均速度、地震波传播时间及地层厚度的统计,6口已钻井地层平均速度在横向上存在着变化,A1井研究层段的平均速度最大,A5井最小,2口井的平均速度相差约为163 m/s,如果利用A1井研究层段的平均速度预测A5井的地层厚度(也可视为深度预测),则与实际值相差约10 m,对于构造幅度只有10~30 m的构造圈闭而言,可能会导致无法反映地下真实形态的构造假象。常规预测方法就存在类似的缺陷。利用研究层内的地震波传播时间和地层厚度关系拟合线性公式来预测地层的厚度,并计算出研究层的地层平均速度,地层厚度的线性拟合公式中相关系数较小,可靠性较低,无法精确地反映研究区的速度变化趋势。这对求取真实的地下构造特征影响大,须要分析影响速度的关键因素,选取合适的速度分析方法准确预测构造特征,指导勘探开发方案的部署。

|
下载原图 图 1 A油田D层段Ⅱ油组的地层平均速度、地震波传播时间及地层厚度统计 Fig. 1 Formation average velocity, seismic wave propaga‐tion time and formation thickness of Ⅱ oil group in layer D of A oilfield |
影响地震波在岩层中传播速度的因素有很多,如岩性、地质年代、埋藏深度、温度、孔隙度、地层结构和孔隙中的流体等。一般情况下,地层的地质年代越老、埋藏越深,地震波的传播速度越快。A油田新近系D层段的埋藏深度为1 250~1 350 m,与地质年代基本一致,对地震波速度的影响程度近乎相同。地层温度随埋藏深度加深而升高,埋藏深度每加深100 m,地层温度升高1~3 ℃,而地层温度每升高100 ℃,速度下降5%~6%,相同埋藏深度对应的温度变化小,对地震波速度影响微小,可忽略不计。因此,地质年代、埋藏深度、温度等因素基本不影响研究层内速度的横向变化。
岩性是影响速度的敏感参数。地震波在不同岩性的地层中传播速度不同,在致密的岩性中传播速度更大,如在泥岩中的传播速度要大于砂岩,若地层中含砂岩比例高,则地层的平均速度小。砂岩储层的实际速度是由砂岩骨架的速度、孔隙度、孔隙流体的速度以及颗粒之间的胶结物成分等因素决定的。
1956年由威利(Wyllie)提出较为合适的关于液体速度、颗粒速度与孔隙度之间的关系式,即时间平均方程
| $ \frac{1}{v} = \frac{\varphi }{{{v_{\rm{f}}}}} + \frac{{1 - \varphi }}{{{v_{\rm{r}}}}} $ | (1) |
式中:v,vf,vr分别为地震波在砂岩,孔隙流体和砂岩基质中的速度,m/s;φ为砂岩的孔隙度,%。经统计A油田D层段含不同流体的砂岩平均孔隙度较接近,一般为30% 左右,对当前研究层而言,孔隙度对层内速度的横向变化影响不大,因此,选取30% 作为孔隙度参数。
将式(1)简化为
| $ v = \frac{1}{{\frac{{0.3}}{{{v_{\rm{f}}}}} + \frac{{0.7}}{{{v_{\rm{r}}}}}}} $ | (2) |
因为vr近似常数,由式(2)可知,v与vf呈正相关关系,即v随vf的增大而增大,反之则减小。已知地震波在含气、含油和含水砂岩中的传播速度是依次递增的,地层中砂岩含气或含油也会使得地层平均速度降低。分析认为,地层中岩性和流体的差异是引起研究层内速度横向变化的主要影响因素。
2.2 平均速度理论表达式的导出地震波在地层中的传播速度是十分重要的参数,但又很难精确测定,在研究过程中对复杂的实际情况进行简化,建立各种简化介质模型,并引入各种速度概念是常用的方法之一[12]。本文将地层平均速度作为研究对象,地震波垂直穿过一组水平层状介质中某一界面以上介质,该界面以上层的总厚度与总的传播时间之比,特指研究层内的地层平均速度,研究层的顶面和底面作为地层平均速度计算的垂向范围。
研究层内n层水平层状介质的平均速度可表达为
| $ {v_{{\rm{av}}}} = \frac{H}{T} = \frac{{\sum\limits_{i = 1}^n {{t_i}{v_i}} }}{{\sum\limits_{i = 1}^n {{t_i}} }} $ | (3) |
式中:vav为研究层段的平均速度,m/s;H为研究层段的总厚度,m;T为地震波穿过研究层段的总传播时间,ms;vi为对应研究层段每个地层的速度,m/s。
在沉积稳定地质条件下,通过平均速度表达式分析影响其变化的敏感参数,并研究平均速度与敏感参数之间的关系。
由式(3)可知,影响研究层段平均速度的参数是H和T。在近似等厚地层的条件下,平均速度只跟传播时间T有关。由A油田的地质特点可知,研究层内地层结构简单,主要由砂岩和泥岩组成。假设研究层段内同一岩性的速度是一致的,式(3)可转换为
| $ {v_{{\rm{av}}}} = \frac{H}{{\frac{{{H_{\rm{s}}}}}{{{v_{\rm{s}}}}} + \frac{{{H_{\rm{m}}}}}{{{v_{\rm{m}}}}}}} = \frac{{{v_{\rm{m}}}}}{{1 + (\frac{{{v_{\rm{m}}}}}{{{v_{\rm{s}}}}} - 1){\varphi _{\rm{s}}}}} = \frac{{{v_{\rm{m}}}}}{{1 + (\sigma - 1){\varphi _{\rm{s}}}}} $ | (4) |
式中:Hs,Hm分别为研究层段内的砂岩厚度和泥岩厚度,m;vs,vm分别为地震波在砂岩和泥岩中的传播速度,m /s;φs为砂地比,即
由式(4)可知,只有φs是变量,其他参数均为已知。因此,vav只跟φs有关系,且两者呈负相关关系,即vav随着φs增大而减小。
上述假定同一岩性的速度是相同的,而针对砂岩受孔隙流体的影响,实际资料中含气、含油和含水砂岩速度是不同的(暂不考虑含流体饱和度的影响)。通常情况下,三者存在依次增大的关系,式(4)可表达为
| $ {v_{{\rm{av}}}} = \frac{H}{{\frac{{{H_{\rm{g}}}}}{{{v_{\rm{g}}}}} + \frac{{{H_{\rm{o}}}}}{{{v_{\rm{o}}}}} + \frac{{{H_{\rm{w}}}}}{{{v_{\rm{w}}}}} + \frac{{{H_{\rm{m}}}}}{{{v_{\rm{m}}}}}}} = \frac{{{v_{\rm{m}}}}}{{[({\sigma _{\rm{g}}} - {\sigma _{\rm{w}}}){\varphi _{\rm{g}}} + ({\sigma _{\rm{o}}} - {\sigma _{\rm{w}}}){\varphi _{\rm{o}}} + {\sigma _{\rm{w}}} - 1]{\varphi _{\rm{s}}} + 1}} $ | (5) |
式中:Hg,Ho,Hw分别为研究层段内的含气砂岩,含油砂岩和含水砂岩的厚度,m;vg,vo,vw分别为地震波在含气砂岩、含油砂岩和含水砂岩中的传播速度,m/s;φg,φo,φw分别为含气砂岩、含油砂岩、含水砂岩所占砂岩总厚度的比率,即
由式(5)可知,φg,φo,φs为变量,其他均为已知,可近似为常数,将式(5)进一步简化
| $ {v_{{\rm{av}}}} = v({\varphi _{\rm{g}}}, {\varphi _{\rm{o}}}, {\varphi _{\rm{s}}}) = {({\theta _1}{\varphi _{\rm{g}}}{\varphi _{\rm{s}}} + {\theta _2}{\varphi _{\rm{o}}}{\varphi _{\rm{s}}} + {\theta _3}{\varphi _{\rm{s}}} + {\theta _4})^{ - 1}} $ | (6) |
将式(6)进行转换
| $ {v^{ - 1}}({\varphi _{\rm{g}}}, {\varphi _{\rm{o}}}, {\varphi _{\rm{s}}}) = {\theta _1}{\varphi _{\rm{g}}}{\varphi _{\rm{s}}} + {\theta _2}{\varphi _{\rm{o}}}{\varphi _{\rm{s}}} + {\theta _3}{\varphi _{\rm{s}}} + {\theta _4} $ | (7) |
由上式可知,研究层段的平均速度可表达为与3个变量φg,φo,φs相关的多元线性方程,其中θ1,θ2,θ3,θ4为未知项,可通过求解方程组得到。
由式(6)可知,地层的平均速度主要跟含气比φg、含油比φo和砂地比φs 3个敏感参数相关。这与在敏感影响参数部分的分析结论一致,其中岩性的差异由砂地比表征,而砂岩孔隙中流体的差异则由含气比和含油比2个参数表征,共同影响了地层平均速度的变化趋势。
2.3 最小二乘法多元线性回归建立平均速度关系式由式(7)可知,式中共有4个未知项,已知A油田已钻多口井,可为式(7)中未知项的求解提供多个样本数据。根据已钻井的信息建立多个方程式组成一个方程组,且方程式的个数大于未知项的个数,这种情况下,平均速度方程组为超定方程组,其表达为
| $ v_i^{ - 1} = \sum\limits_{j = 1}^n {{\varphi _{ij}}{\theta _j}} , (i = {\rm{ }}1, 2, 3 \cdots m) $ | (8) |
式中:φij为方程式的变量;θj为方程式的未知项;m为方程的数量,个;n为未知数的数量,个,且m > n。
将式(8)向量化
| $ \mathit{\boldsymbol{v}} = \mathit{\boldsymbol{\varphi \theta}} , \mathit{\boldsymbol{v}} = \left[ {\begin{array}{*{20}{c}} {v_1^{ - 1}}\\ {v_2^{ - 1}}\\ \vdots \\ {v_n^{ - 1}} \end{array}} \right], \mathit{\boldsymbol{\varphi}} = \left[ {\begin{array}{*{20}{c}} {{\varphi _{11}}}&{{\varphi _{12}}}& \cdots &{{\varphi _{1n}}}\\ {{\varphi _{21}}}&{{\varphi _{21}}}& \cdots &{{\varphi _{2n}}}\\ \vdots & \vdots &{}& \vdots \\ {{\varphi _{m1}}}&{{\varphi _{m2}}}& \cdots &{{\varphi _{mn}}} \end{array}} \right], \mathit{\boldsymbol{\theta}} = \left[ {\begin{array}{*{20}{c}} {{\theta _1}}\\ {{\theta _2}}\\ \vdots \\ {{\theta _n}} \end{array}} \right] $ | (9) |
该超定方程组理论上是一个不存在唯一解的矛盾方程,通常是利用最小二乘法来求取其最优解。最小二乘法(又称最小平方法)是一种数学优化技术,通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法引入残差平方和函数S,记作S (θ) =|| φθ - v||2,求取S函数的最小值min||φθ - v||2,使得计算结果更加接近真实值,进而求解出未知数θ,得出平均速度的表达式。
3 数值模拟分析数值模拟是利用已知的钻井与测井等资料建立简化的地质模型,根据地震波在地下介质中的传播原理,通过如射线追踪或波动方程偏移等数学方法模拟地震记录[13-15],统计分析研究层内平均速度与砂地比、含气比和含油比的关系,建立数值模拟的地层平均速度表达式,并分析计算结果与实际结果的对比关系。
建立二维地质模型[图 2(a)],设置研究层段厚度为100 m,分别建立2组地层结构,第一组为不区分流体的5个砂岩模型,砂岩厚度的百分比从10% 增加至50%,第二组为含不同流体的5个砂岩模型,包括含气、含油和含水砂岩,其砂岩所占比例存在变化,但总砂岩厚度的百分比依然从10% 增加至50%。根据实钻井信息设置速度参数,将地震波在含气砂岩、含油砂岩、含水砂岩、砂岩和泥岩中的传播速度分别设置为1 800 m/s,2 000 m/s,2 300 m/s,2 200 m/s,2 800 m/s。以图 2(a)中的蓝线为目标界面,采用35 Hz负极性雷克子波(与实际地震资料一致),目标界面在波形剖面上对应图 2(b)中蓝线所在的波峰位置。
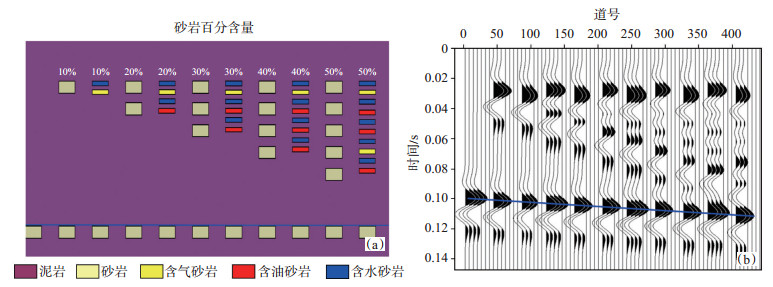
|
下载原图 图 2 数值模拟中建立的地质模型(a)及正演模拟剖面(b) Fig. 2 Geological model (a) and forward simulation section (b) established in numerical simulation |
在数值模拟[图 2(b)]中,不论砂岩内部是否区分流体,随着砂地比的增加,从研究顶面到目标界面的旅行时都是逐渐增加,即平均速度逐渐减小,两者基本呈线性负相关关系,且在砂地比相同的情况下,区分流体的砂岩平均速度小于不区分流体的砂岩。因此,数值模拟证实岩性的差异和砂岩内部孔隙流体的差异是影响平均速度的关键因素。
图 3为平均速度与含气比、含油比和砂地比的关系分析图,单一的含气比或含油比与平均速度并没有明显的线性关系,可采用非线性拟合。
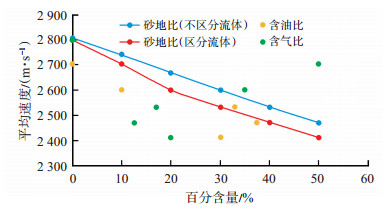
|
下载原图 图 3 平均速度与含气比、含油比和砂地比的关系 Fig. 3 Relationships of average velocity with gas-sand ratio, oil-sand ratio and sand-strata ratio |
根据模型中的样本数据通过最小二乘法可求解出平均速度关系式的未知项,可得
| $ {v_{{\rm{av}}}} = \frac{{{{10}^4}}}{{(3.155 - 4.109{\varphi _{\rm{g}}} - 3.94{\varphi _{\rm{o}}}){\varphi _{\rm{s}}} + 3.582}} $ | (10) |
在砂岩内部区分流体的情况下,平均速度表达式是由砂地比、含气比和含油比3个参数共同组成的多元线性公式,其中,平均速度与砂地比基本呈负相关关系,而与含气比或含油比单因素并无简单的线性关系。通过对比平均速度的计算结果与实际数值(图 4)可知,两者基本一致,绝对误差最大仅为11 m/s,相对误差最大为0.4%,计算结果具有较高的预测精度。式(10)在地层结构简单(砂泥组合)、岩性速度相近的稳定沉积地质条件下具有较好的适用性。
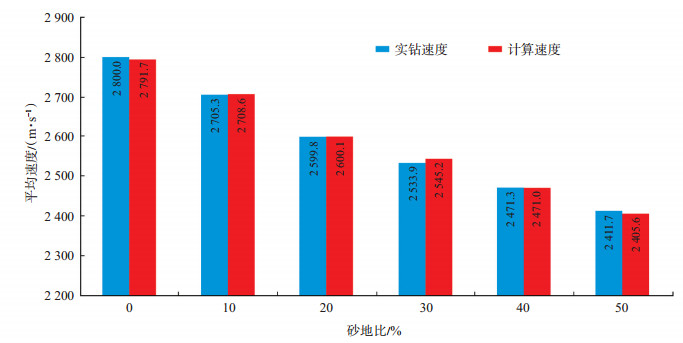
|
下载原图 图 4 A油田D层段实钻结果与计算值对比 Fig. 4 Correlation of actual drilling results and calculated values in layer D of A oilfield |
由A油田D层段内已钻井信息统计(表 1)可知,地震波在砂岩中的传播速度小于泥岩,而在含气、含油和含水砂岩中的传播速度是依次增大的。
|
|
下载CSV 表 1 A油田已钻井D层段不同岩性的介质参数 Table 1 Medium parameters of different lithologies in layer D of A oilfield |
表 2为A油田D层段内的6口井含油气性统计,A5井的砂地比和含油比最高,对应的平均速度最小,A1,A2和A3等3口井研究层段内均不含气,A1井的砂地比最小,对应的平均速度最大,与上述分析和数值模拟的结论一致。
|
|
下载CSV 表 2 A油田6口井D层段的含油气性统计 Table 2 Hydrocarbon-bearing properties of 6 wells in layer D of A oilfield |
根据含气比、含油比和砂地比的统计结果(表 2),综合式(7),可建立由多个方程式构成一个超定方程组,通过最小二乘法可求解出平均速度关系式的未知项,则A油田D层Ⅱ油组的平均速度非线性拟合公式为
| $ {v_{{\rm{av}}}} = \frac{{{{10}^6}}}{{(6.1 + 230.8{\varphi _{\rm{g}}} + 69.5{\varphi _{\rm{o}}}){\varphi _{\rm{s}}} + 405.8}} $ | (11) |
将本文方法、常规线性拟合方法和实际平均速度对比分析(表 3)可知,常规方法计算结果与实际值误差大,特别是A5井和A6井,绝对误差最大为198.8 m/s,相对误差最大为8.6%,而多元线性回归法计算结果与实际值误差小,绝对误差最大为13.2 m/s,相对误差最大0.6%,本文方法的计算结果更接近实际值,具有较高的预测精度。同时,也表明了在与A油田类似的地质条件下,常规的线性拟合方法在预测低速区域时误差较大,无法真实还原构造特征,特别在构造缓的研究区,严重影响了勘探开发方案的部署,而本文的多元线性回归法在低速区域预测结果依然精准,可以很好地弥补常规方法的不足,真实反映地下的构造特征,有利于油田的精细勘探开发。
|
|
下载CSV 表 3 A油田D层被本文方法与常规方法计算的平均速度与实际数值的对比 Table 3 Average velocity correlation of calculated by this method and the conventional method with actual value in layer D of A oilfield |
(1)数值模拟证实:砂岩储层岩性的差异和砂岩内部流体的差异是影响地层平均速度的关键因素,岩性的差异可以由砂地比表征,孔隙中流体的差异则由含气比和含油比2个参数表征,含气比、含油比和砂地比3个参数共同影响了地层平均速度的变化趋势。
(2)对沉积条件稳定的地层,其平均速度可以表示为由含气比、含油比和砂地比3个参数组成的多元线性拟合公式,且平均速度跟砂地比呈负相关关系,随砂地比的增加而减小,而与含气比或含油比单因素并无简单的线性关系。该线性拟合公式求取的平均速度计算值与实际值误差较小,具有较高的预测精度。
| [1] |
李伍志, 王璞珺, 张功成, 等. 珠江口盆地深部基底地层的地震时深转换研究. 地球物理学报, 2011, 54(2): 449-456. LI W Z, WANG P J, ZHANG G C, et al. Researches on timedepth conversion of deep-seated basal strata of Pearl River Mouth Basin. Chinese Journal of Geophysics, 2011, 54(2): 449-456. DOI:10.3969/j.issn.0001-5733.2011.02.023 |
| [2] |
RUSSELL B. A simple seismic imaging exercise. The Leading Edge, 1998, 19(7): 885-889. |
| [3] |
王华忠, 冯波, 李辉, 等. 各种速度分析与反演方法的对比研究. 岩性油气藏, 2012, 24(5): 1-11. WANG H Z, FENG B, LI H, et al. Comparison among velocity analysis and inversion methods. Lithologic Reservoirs, 2012, 24(5): 1-11. DOI:10.3969/j.issn.1673-8926.2012.05.001 |
| [4] |
陈林, 邓勇, 盖永浩, 等. 复杂断块构造时深转换方法探讨: 以涠西南凹陷为例. 地球物理学进展, 2014, 29(3): 1121-1127. CHEN L, DENG Y, GAI Y H, et al. Exploration of time-depth conversion method in complicated fault block: Take Weixinan sag for example. Progress in Geophysics, 2014, 29(3): 1121-1127. |
| [5] |
韩令贺, 胡自多, 冯会元, 等. 井震联合网格层析各向异速度建模研究及应用. 岩性油气藏, 2018, 30(4): 91-97. HAN L H, HU Z D, FENG H Y, et al. Grid tomography based on well-to-seismic integration in anisotropic velocity modeling and its application. Lithologic Reservoirs, 2018, 30(4): 91-97. |
| [6] |
孔庆河, 李铭铭, 张文德. 地震勘探中平均速度的求取方法及应用. 辽宁工程大学学报(自然科学版), 2012, 31(1): 54-56. KONG Q H, LI M M, ZHANG W D. Calculation method of average velocity in seismic exploration and its application. Journal of Liaoning Technical University(Natural Science Edition), 2012, 31(1): 54-56. DOI:10.3969/j.issn.1008-0562.2012.01.013 |
| [7] |
徐立恒, 鲜波, 薛玉英, 等. 高精度地震时深转换方法研究及应用. 吉林大学学报(地球科学版), 2014, 44(5): 1712-1719. XU L H, XIAN B, XUE Y Y, et al. Study and application on seismic time-depth conversion with high-precision. Journal of Jilin University(Earth Science Edition), 2014, 44(5): 1712-1719. |
| [8] |
边立恩, 于茜, 谷志猛, 等. 低速异常带平均速度场建模方法研究. 岩性油气藏, 2015, 27(3): 122-126. BIAN L E, YU Q, GU Z M, et al. Research on mean velocity field modeling method for low velocity anomaly zone: A case study from Q oilfield, Bohai. Lithologic Reservoirs, 2015, 27(3): 122-126. DOI:10.3969/j.issn.1673-8926.2015.03.019 |
| [9] |
梁卫, 李熙盛, 罗东红, 等. 井震时深转换技术在低幅度构造评价中的应用. 中国海上油气, 2014, 26(3): 61-64. LIANG W, LI X S, LUO D H, et al. Applying a technique of borehole seismic time-depth conversion to the evaluation of low relief structures. China Offshore Oil and Gas, 2014, 26(3): 61-64. |
| [10] |
蔡刚, 刘化清, 姚军, 等. 变速成图方法应用: 以歧南斜坡区为例. 地球物理学进展, 2015, 30(2): 947-953. CAI G, LIU H Q, YAO J, et al. Application of variable velocity structure mapping method: A case study of Qinan slope area. Progress in Geophysics, 2015, 30(2): 947-953. |
| [11] |
虞永征, 杨长清. 东海陆架盆地南部区域地震速度分析. 海洋地质前沿, 2018, 34(4): 63-70. YU Y Z, YANG C Q. Analysis of velocity data from the south of East China Sea shelf basin. Marine Geology Frontiers, 2018, 34(4): 63-70. |
| [12] |
陆基孟. 地震勘探原理. 北京: 中国石油大学出版社, 2008: 195-203. LU J M. Principle of seismic exploration. Beijing: China University of Petroleum Press, 2008: 195-203. |
| [13] |
余为维, 冯磊, 杜艳艳. 旬邑地区野外露头岩性组合地震反射特征研究. 特种油气藏, 2018, 25(5): 24-29. YU W W, FENG L, DU Y Y. Seismic reflection characterization of field outcrop lithology association in Xunyi. Special Oil and Gas Reservoirs, 2018, 25(5): 24-29. DOI:10.3969/j.issn.1006-6535.2018.05.005 |
| [14] |
胡修权, 施泽进, 王长城, 等. 涪陵地区飞仙关组储层地球物理响应特征及正演模拟. 地球物理学进展, 2014, 29(3): 1148-1156. HU X Q, SHI Z J, WANG C C, et al. Reservoir geophysical response feature and forward modeling of Feixianguan Formation in Fuling area, southeastern Sichuan Basin. Progress in Geophysics, 2014, 29(3): 1148-1156. |
| [15] |
苑雅轩, 樊太亮, 苑学军, 等. 塔河油田蓬莱坝组异常地震特征及地质成因分析. 岩性油气藏, 2018, 30(6): 98-108. YUAN Y X, FAN T L, YUAN X J, et al. Characteristics and geological genesis of anomalous seismic facies of Penglaiba Formation in Tahe Oilfield. Lithologic Reservoirs, 2018, 30(6): 98-108. |
 2021, Vol. 33
2021, Vol. 33



