多孔介质中的气体扩散问题是能源开采、燃料电池、化学工程等领域研究的重点,但是气体在多孔介质中的扩散包含了很多复杂的传质机理,如何建立多孔介质中气体有效扩散系数模型成为研究热点[1]。
传统的物质扩散定律一般由菲克定律来描述,该定律描述了物质扩散通量与浓度梯度之间的定量关系。Cao等[2]通过建立多孔介质三维模型,证明在稳态情况下,菲克定律能够在多孔介质气体扩散中适用,然而该模型使用的是100×100×100的立方网络模型,对于多孔介质的不规则性和复杂性方面的描述不够准确。气体在多孔介质中复杂的输运机理与多孔介质孔隙大小和结构差异有很大关系,根据多孔介质孔隙大小和结构的不同,多孔介质中的气体流动与扩散常常划分为4个流动区域:连续介质区、滑移区、过渡区和自由分子区[3]。Beskok等[4]通过大量实验给出了一维圆管中气体体积流量的表达式,该表达式引入克努森数kn和渗透率修正因子f(kn),可以适用于所有流动区域。符东宇等[5] 运用格子Boltzmann方法研究了页岩气藏的渗流规律,发现克努森数kn是影响页岩气渗流的主要参数。Roy等[6]使用Ar,N2,O2和Al2O3作为实验材料进行了扩散实验,引入了克努森扩散系数,建立了微纳米孔道中的气体扩散方程,但是该方程只能适用于自由分子区。张烈辉等[7]考虑了多重运移机制,建立了页岩气藏的综合渗流模型。李亚雄等[8] 通过研究页岩气的滑脱和扩散机理,提出了“壁联扩散”的新概念来表征克努森扩散和表面扩散的总效应,但该方法的数学模型与论证过程还有待完善。在一些科学研究和实际情况中,例如川南地区页岩孔隙结构和川西坳陷致密砂岩孔隙结构,它们的孔道直径很小,达到了微纳米级别,此时,孔隙结构显示出分形的特性。陈居凯等[9],朱汉卿等[10]和邓浩阳等[11]均使用分形理论研究了页岩与致密砂岩等致密多孔介质的孔隙结构。目前,也有很多文献将分形理论运用到气体渗透和扩散中[12-14]。Zheng等[15]基于分形理论和毛细管束模型,得到了气体的有效扩散系数模型。该模型能与已有实验数据相吻合,并且能适用于不同的多孔介质。Shi等[16]在考虑了2种运输机制的情况下,运用分形理论建立了H2在燃料电池气体扩散层中的有效扩散系数模型,并且分析了分形理论相关参数(孔隙度、分形维数等)的影响。Zhang[17]考虑了3种多孔介质中的气体流动机理,得到了渗透率和气体有效扩散分形模型,但忽略了气体的滑脱效应。Woignier等[18]研究了分形多孔介质中气体在滑移区的扩散机理并建立了滑移模型。张赛等[19]和牟新竹等[20]在研究多尺度分形多孔介质气体扩散时加入了孔隙连通性参数,得到了新的数学模型。以上研究大多只考虑了1种或2种气体扩散机理,不能完整地描述气体在多孔介质中的扩散问题。
基于Beskok等[4]给出的表达式、迂曲毛细管束模型、分形理论和菲克定律,建立气体在多孔介质中扩散的分形模型;该模型包含面积分形维数、迂曲分形维数、孔隙度、最大最小孔隙直径、气体密度、黏度、摩尔质量等参数,然后分析这些参数与气体有效扩散系数之间的函数关系与变化趋势,以期能够正确地描述气体在多孔介质中的扩散规律,并应用于油气田的开发。
1 多孔介质的分形特征 1.1 孔隙数目与横截面积描述在具有分形特性的多孔介质中,孔隙直径大于等于λ的孔隙数量的总和与孔隙直径大小满足下面的分形标度关系[21]
| $ N(L \geqslant \lambda)=\left(\frac{\lambda_{\max }}{\lambda}\right)^{D_{\mathrm{f}}} $ | (1) |
式中:N为孔隙长度大于孔隙直径的多孔介质的孔隙总数目;L为毛细管长度,m;λmax与λ分别为最大孔隙直径和孔隙直径,m;Df为无因式多孔介质的面积分形维数。
在真实多孔介质中,孔隙数目十分巨大,根据统计理论和方法,可以将式(1)看成是连续和可微的函数,对式(1)进行微分可以得到
| $ -\mathrm{d} N=D_{\mathrm{f}} \lambda_{\max }^{D_{\mathrm{f}}} \lambda^{-\left(D_{\mathrm{f}}+1\right)} \mathrm{d} \lambda $ | (2) |
式(2)得到了在(λ, λ+ d λ)的孔隙数目,表明了孔隙数目随着孔隙直径的增大而减少,-dN > 0。由于截面上的孔隙可以看作是直径不同的圆,因此通过式(2),用微元法可得到分形集中截面上总的孔隙面积AP为
| $ \begin{aligned} A_{\mathrm{P}} &=-\int_{\lambda_{\min }}^{\lambda_{\max }} \frac{1}{4} {\rm{ \mathsf{ π}}} \lambda^{2} \mathrm{~d} N \\ &=\int_{\lambda_{\min }}^{\lambda_{\max }} \frac{1}{4} {\rm{ \mathsf{ π}}} \lambda^{2} D_{\mathrm{f}} \lambda_{\max }^{D_{\mathrm{f}}} \lambda^{-\left(D_{\mathrm{f}}+1\right)} \mathrm{d} \lambda \\ &=\frac{{\rm{ \mathsf{ π}}} D_{\mathrm{f}} \lambda_{\max }^{2}}{4\left(2-D_{\mathrm{f}}\right)}\left[1-\left(\frac{\lambda_{\min }}{\lambda_{\max }}\right)^{2-D_{\mathrm{f}}}\right] \end{aligned} $ | (3) |
式中:AP为截面上的总的孔隙面积,m2;λmin为最小孔隙直径,m。
则总的截面积At可以计算得到
| $ A_{\mathrm{t}}=\frac{A_{\mathrm{P}}}{\varepsilon}=\frac{{\rm{ \mathsf{ π}}} D_{\mathrm{f}} \lambda_{\max }^{2}}{4 \varepsilon\left(2-D_{\mathrm{f}}\right)}\left[1-\left(\frac{\lambda_{\min }}{\lambda_{\max }}\right)^{2-D_{\mathrm{f}}}\right] $ | (4) |
式中:At为总的截面积,m2;ε为面孔隙度。
一般情况下,体孔隙度和面孔隙度不相等,两者之间相差一个迂曲度因子
| $ \bar{\tau}=\frac{\varPhi}{\varepsilon} $ | (5) |
式中:Φ为体孔隙度;τ为迂曲度因子[1]。在计算多孔介质相关参数时通常使用的是体孔隙度,通过式(5)可以实现面孔隙度与体孔隙度的转化。
上述式(1)-(5)描述了多孔介质内部结构和孔隙分布情况,是描述多孔介质内部输运物理现象的重要公式。
1.2 孔隙迂曲特征描述假设多孔介质是由一束横截面积不同的迂曲毛细管道组成,在该模型中,单根迂曲毛细管道的长度L (λ) 与管道直径λ的关系满足分形幂规律,表示为
| $ L(\lambda)=\lambda^{1-D_{\rm{t}}} L_{0}^{D_{\rm{t}}} $ | (6) |
式中:L0为毛细管流动方向的特征长度,m。根据分形理论,L0可以通过L0 =
| $ \tau=\frac{L(\lambda)}{L_{0}}=\left(\frac{L_{0}}{\lambda}\right)^{D_{\rm{t}}-1} $ | (7) |
气体在多孔介质中的扩散问题影响因素众多,其中孔隙结构为主要的影响因素。当孔隙直径不同时,气体扩散的规律也不同。Beskok等[4]通过实验给出了描述气体在一维圆管中气体体积流量的模型,该模型根据Hagen-Poiseuille方程修正得到,其表达式为
| $ q(\lambda)=f(k n) \frac{{\rm{ \mathsf{ π}}} \Delta p}{128 \mu} \frac{\lambda^{4}}{L(\lambda)} $ | (8) |
式中:kn为克努森数,kn= l/λ,定义为气体分子的平均自由程l与孔隙直径λ的比值,l的单位为m;Δp为毛细管中的气体压力差,Pa;μ为气体黏度,Pa∙s。f(kn)为渗透率修正因子,此因子只与kn有关,其表达式为
| $ f(k n)=(1+\alpha\ k n)\left(1+\frac{4 k n}{1+k n}\right) $ | (9) |
| $ \alpha=\frac{128}{15 {\rm{ \mathsf{ π}}}^{2}} \arctan \left(4 k n^{0.4}\right) $ | (10) |
根据kn的不同,气体在致密多孔介质中可以分为连续介质区、滑移区、过渡区和自由分子区等4个流动区域,但是,将式(9)和式(10)代入式(8)后得到的公式具有很强的非线性特征,不易求解,应用价值不大[22]。为了得到广泛适用的渗透率修正因子,使用matlab多项式曲线拟合工具,对式(9)进行分段拟合。
当kn≤0.001和0.001 < kn≤0.100时,气体流动处于连续介质区和滑移区。运用泰勒公式将式(10)化简后再代入式(9),然后忽略渗透率修正因子的二阶和高阶修正,保留一级修正。此时,f(kn) = 1 + 4 kn,据文献[23]报道,该公式正是Klinkengerg于1941年给出的考虑滑脱效应的气测渗透率的数学表达式,这里的4kn即为滑移因子,但是忽略了二阶和高级修正会导致简化模型值小于Beskok模型值,而通过曲线拟合的方式得到的拟合公式f(kn) = 1 + 4.8 kn其简化模型值与Beskok模型值比较吻合。相对误差为0.060%~0.272%,度量拟合优度的统计量r2可达0.999 4。
当0.1 < kn≤ 10.0和kn> 10时,气体处于过渡区和自由分子区。过渡区的拟合公式为f(kn) = 0.8 + 6.2kn,相对误差为1.3%~8.5%,统计量r2为0.992。自由分子区的拟合公式为f(kn) = -4.1 + 6.65kn,相对误差为0.11%~1.93%,统计量r2为0.999。
综上,通过对渗透率修正因子曲线拟合而简化得到的模型如下
| $ f(k n)=\left\{\begin{array}{ll} 1+4.8 k n, & 0<k n \leqslant 0.1 \\ 0.8+6.2 k n, & 0.1<k n \leqslant 10 \\ -4.1+6.65 k n, & 10<k n \end{array}\right. $ | (11) |
通过对式(8)的拟合得到分段函数与原函数的对比(图 1),可以看出简化后的模型与原模型拟合误差较小,精确度较高。通过对渗透率修正因子的简化,不仅为后续理论计算和求解提供了基础,同时也有利于Beskok模型的推广。
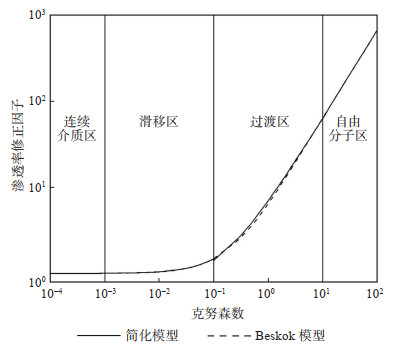
|
下载原图 图 1 Beskok模型与简化模型的对比 Fig. 1 Comparison between Beskok model and simplified model |
所以一维圆管中气体体积流量公式也可以用一个分段函数来描述
| $ q(\lambda)=\left\{\begin{array}{l} q_{\mathrm{p}}=(1+4.8{kn}) \frac{{\rm{ \mathsf{ π}}} \Delta p}{128 \mu} \frac{\lambda^{4}}{L(\lambda)}, \quad k n \leqslant 0.1 \\ q_{\mathrm{pk}}=(0.8+6.2 {kn}) \frac{{\rm{ \mathsf{ π}}} \Delta p}{128 \mu} \frac{\lambda^{4}}{L(\lambda)}, 0.1<k n \leqslant 10 \\ q_{\mathrm{k}}=(-4.1+6.65{kn}) \frac{{\rm{ \mathsf{ π}}} \Delta p}{128 \mu} \frac{\lambda^{4}}{L(\lambda)}, 10<{kn} \end{array}\right. $ | (12) |
由于多孔介质具有不规则性和复杂性,在同一多孔介质中孔隙大小差别很大,这使得多种流动区域在同一多孔介质中同时存在,根据气体流动区域的划分,计算气体通过横截面的流量公式如下[17]
| $ Q=-\int_{\lambda_{\text {min }}}^{\lambda_{\mathrm{k}}} q_{\mathrm{k}}(\lambda) \mathrm{d} N-\int_{\lambda_{\mathrm{k}}}^{\lambda_{\mathrm{p}}} q_{\mathrm{pk}}(\lambda) \mathrm{d} N-\int_{\lambda_{\mathrm{p}}}^{\lambda_{\max }} q_{\mathrm{p}}(\lambda) \mathrm{d} N $ | (13) |
式中:λk = 0.1 l为滑移区和过渡区的临界直径;λp = 10 l为过渡区和自由分子区的临界直径。
联合式(2)、式(5)、式(11)和式(12)可得
| $ \begin{aligned} Q=& \frac{{\rm{ \mathsf{ π}}} D_{\mathrm{f}} \lambda_{\max }^{D_{\mathrm{f}}} \Delta p}{128 \mu L_{0}^{D_{\mathrm{t}}}\left(3+D_{\mathrm{t}}-D_{\mathrm{f}}\right)}\left(\lambda_{\max }^{3+D_{\mathrm{t}}-D_{\mathrm{f}}}-0.2 \lambda_{\mathrm{p}}^{3+D_{\mathrm{t}}-D_{\mathrm{f}}}-4.9 \lambda_{\mathrm{k}}^{3+D_{\mathrm{t}}-D_{\mathrm{f}}}+4.1 \lambda_{\min }^{3+D_{\mathrm{t}}-D_{\mathrm{f}}}\right)+\\ & \frac{{\rm{ \mathsf{ π}}} D_{\mathrm{f}} \lambda_{\max }^{D_{\mathrm{f}}} \Delta p l}{128 \mu L_{0}^{D_{\mathrm{t}}}\left(2+D_{\mathrm{t}}-D_{\mathrm{f}}\right)}\left(4.8 \lambda_{\max }^{2+D_{\mathrm{t}}-D_{\mathrm{f}}}+1.4 \lambda_{\mathrm{p}}^{2+D_{\mathrm{t}}-D_{\mathrm{f}}}+0.45 \lambda_{\mathrm{k}}^{2+D_{\mathrm{t}}-D_{\mathrm{f}}}-6.65 \lambda_{\min }^{2+D_{\mathrm{t}}-D_{\mathrm{f}}}\right) \end{aligned} $ | (14) |
根据菲克定律,气体在多孔介质中扩散的总的摩尔流率为[15]
| $ Q_{\mathrm{F}}=\frac{A_{\mathrm{t}} D_{\mathrm{eff}} \Delta C}{L_{0}} $ | (15) |
式中:QF为气体摩尔流率,mol/s;At为多孔介质总的截面积,m2;Deff为有效扩散系数,m2/s;ΔC为多孔介质孔道两端的浓度差,ΔC = Δp/ (RT),其中,R为气体常数8.314J/ (mol · K);T为温度,K。计算时须要将气体摩尔流率转化为气体体积流量。
联合式(5)、式(6)、式(13)和式(14),可以求出
| $ \begin{array}{l} {D_{{\rm{eff }}}} = \left[ {\begin{array}{*{20}{c}} {\frac{{{\rm{ \mathsf{ π} }}{D_{\rm{f}}}\lambda _{\max }^{{D_{\rm{t}}}}RT\rho }}{{128\mu L_0^{{D_{\rm{t}}} - 1}\left( {3 + {D_{\rm{t}}} - {D_{\rm{f}}}} \right)M}}\left( {\lambda _{\max }^{3 + {D_{\rm{t}}} - {D_{\rm{f}}}} - 0.2\lambda _{\rm{p}}^{3 + {D_{\rm{t}}} - {D_{\rm{f}}}} - 4.9\lambda _{\rm{k}}^{3 + {D_{\rm{t}}} - {D_{\rm{f}}}} + 4.1\lambda _{\min }^{3 + {D_{\rm{t}}} - {D_{\rm{f}}}}} \right) + }\\ {\frac{{{\rm{ \mathsf{ π} }}{D_{\rm{f}}}\lambda _{\max }^{{D_{\rm{f}}}}{\rm{R}}T\rho l}}{{128\mu L_0^{{D_{\rm{t}}} - 1}\left( {2 + {D_{\rm{t}}} - {D_{\rm{f}}}} \right)M}}\left( {4.8\lambda _{\max }^{2 + {D_{\rm{t}}} - {D_{\rm{f}}}} + 1.4\lambda _{\rm{p}}^{2 + {D_{\rm{t}}} - {D_{\rm{f}}}} + 0.45\lambda _{\rm{k}}^{2 + {D_{\rm{t}}} - {D_{\rm{f}}}} - 6.65\lambda _{\min }^{2 + {D_{\rm{t}}} - {D_{\rm{f}}}}} \right)} \end{array}} \right] \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{{\frac{{{\rm{ \mathsf{ π} }}{D_{\rm{f}}}\lambda _{\max }^2}}{{4\varepsilon \left( {2 - {D_{\rm{f}}}} \right)}}\left[ {1 - {{\left( {\frac{{{\lambda _{\min }}}}{{{\lambda _{\max }}}}} \right)}^{2 - {D_f}}}} \right]}} \end{array} $ | (16) |
式(16)是基于渗透率修正因子、迂曲毛细管束模型、分形理论和菲克定律求出来的多孔介质气体扩散模型。此模型的每一个参数都具有物理意义,不包含经验常数。式(16)表明,气体有效扩散系数与多孔介质面积分形维数、迂曲分形维数、孔隙度、温度、最大与最小孔隙直径、气体分子平均自由程、气体摩尔质量、气体密度和黏度等均有关,并且描述了在不同流动区域共同作用下多孔介质中气体扩散的详细机理。
通过式(16)可得知这些参数对气体有效扩散系数的影响,并应用于工程实践中的相关参数分析。
3 分析和讨论本文建立的气体有效扩散系数包含了2类参数。一类是关于多孔介质孔隙数目和结构的参数,如多孔介质面积分形维数、迂曲分形维数、特征长度、孔隙度等。另一类是关于气体的性质参数,如密度、摩尔质量、黏度、气体分子平均自由程等。
多孔介质的结构参数通过分形理论的描述和计算得出,面积分形维数由以下公式来确定
| $ D_{\mathrm{f}}=D_{\mathrm{E}}-\frac{\ln \varepsilon}{\ln \frac{\lambda_{\min }}{\lambda_{\max }}} $ | (17) |
式中:DE为欧几里德维数,在二维空间中,DE = 2;在三维空间中,DE = 3。该文是在二维平面上建立的模型,所以DE = 2。Feng等[24]归纳了孔隙度和面积分形维数的实验数据,结果显示当λmin/λmax ≈ 10-3时,理论模型值与实验结果比较吻合。
对于迂曲分形维数,尹帅等[25]分析了常规及非常规储层岩石的分形特征。运用压汞法和吸附法研究得到了具有分形特性的多孔介质的迂曲分形维数,其中砂岩多孔介质的迂曲分形维数为1.207 ~1.704,页岩多孔介质的迂曲分形维数为1.668~2.187。
然后将已有实验数据与本文提出的有效扩散系数的理论模型进行对比。Currie[26]将H2作为扩散气体,使用了多种不同的多孔介质来进行扩散实验。须要注意的是,实验中一般使用体孔隙度,而理论模型中是用面孔隙度。须要借助关系式Φ= τε,把面孔隙度转化为体孔隙度。其中τ = 1 + 0.63ln(1/Φ),该公式由实验数据拟合得到[1]。
表 1为建立的模型的部分参数:
|
|
下载CSV 表 1 分形模型中的部分参数与数值 Table 1 Some parameters and values in the fractal model |
将以上数据和公式(17)代入式(16)可以得到图 2中的函数关系,图 2显示气体有效扩散系数的预测值随着孔隙度的增加而增加,因为随着孔隙度的增加,气体扩散的区域和路径会增多,有效扩散系数相应增加。当孔隙度超过0.65时,模型预测值会低于实际值,因为该模型中的最大孔隙直径使用的是固定值。通过对比模型预测值与实验数据,可知该模型能够准确地计算气体在分形多孔介质中的有效扩散系数。本次建立的理论模型可以用于多孔介质微纳米级孔隙情况下的单相气体扩散计算,可以为非常规天然气资源开采提供关键参数,也可以为气液两相或者多相渗透与扩散提供参考。
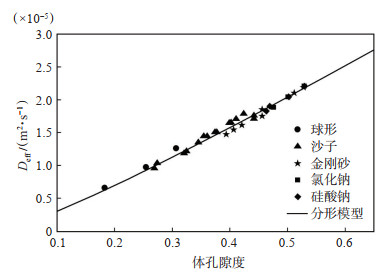
|
下载原图 图 2 分形模型的气体有效扩散系数与文献[26] 实验数据对比 Fig. 2 Comparison of effective gas diffusion coefficient of fractal model with experimental data in reference |
图 3为孔道迂曲分形维数分别取1.5,1.6,1.7时,气体有效扩散系数随着多孔介质面积分形维数的变化趋势。从图 3可以得出,面积分形维数越大,气体有效扩散系数也越大。因为面积分形维数增加时,孔隙数目也会增加,孔隙度也会增大,导致扩散相对更加容易。当面积分形维数一定时,迂曲分形维数增加,气体有效扩散系数会减小。因为迂曲分形维数越大,表明孔道毛细管越弯曲,扩散阻力越大,导致扩散性能减小。
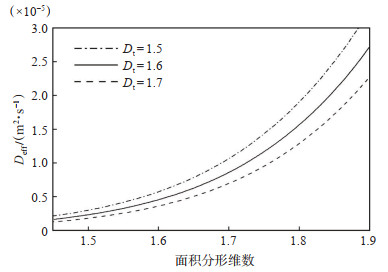
|
下载原图 图 3 面积分形维数和迂曲分形维数对气体有效扩散系数的影响 Fig. 3 Effect of area fractal dimension and tortuous frac‐ tal dimension on effective gas diffusion coefficient |
图 4为考虑滑移因子的模型与不考虑滑移因子模型的对比。据文献[23]报道,Klinkengerg于1941年发现了滑移现象,具体表现为气体的表观渗透率明显大于绝对渗透率。从图 4可以看出当考虑滑移因子时,气体的有效扩散系数大于未考虑滑移因子的气体有效扩散系数,这与Klinkengerg描述的现象一致。由图 4分析可知,在孔隙直径较大的情况下,滑移因子的影响越来越小,当孔隙直径较小时,滑移因子对有效扩散系数的影响较大,这与滑脱效应一般发生在低渗透率和低孔隙度相一致。从图 4还可以看出,考虑了滑移因子的分形模型与不同多孔介质的实验数据更加吻合,这表明考虑了滑移因子的分形模型能够适用于更多种类的多孔介质。
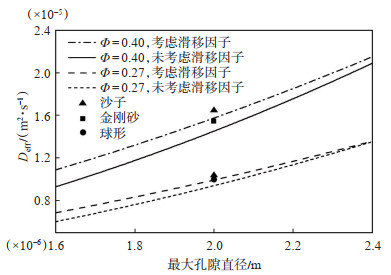
|
下载原图 图 4 滑移因子对气体有效扩散系数的影响 Fig. 4 Effect of slip factor on effective gas diffusion coefficient |
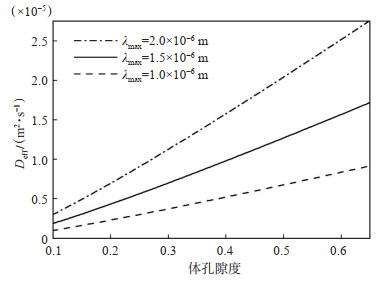
图 5为在不同最大孔隙直径下,有效扩散系数随孔隙度变化的情况。
|
下载原图 图 5 最大孔隙直径对气体有效扩散系数的影响 Fig. 5 Effect of maximum pore diameter on effective gas diffusion coefficient |
从图 5可以得出,当最大孔隙直径减小时,气体有效扩散系数也会减小。因为根据分形理论,分形多孔介质的面积分形维数、迂曲分形维数、最小最大孔径比、扩散截面面积等都与最大孔隙直径有关,所以最大孔隙直径是气体有效扩散系数的主要影响因素。
图 6为使用不同的扩散气体时,有效扩散系数随孔隙度的变化。由图 6可知,不同的气体在多孔介质中的有效扩散系数不同,当扩散的气体的摩尔质量,或者气体密度增加时,有效扩散系数会减小。因为气体质量越大,扩散速率就会越小,有效扩散系数也会越小,这与气体扩散定律描述的现象一致。
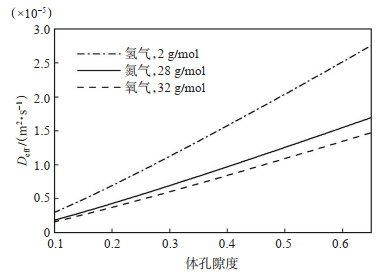
|
下载原图 图 6 不同气体对气体有效扩散系数的影响 Fig. 6 Effect of different kinds of gases on effective gas diffusion coefficient |
(1)基于多孔介质的分形特征、迂曲毛细管束模型、菲克定律、渗透率修正因子建立了多孔介质中气体扩散的分形模型。该模型包含了多孔介质面积分形维数、迂曲分形维数、孔隙度、最大孔隙直径、气体密度和摩尔质量等参数。通过参数分析可以发现:多孔介质孔隙度、面积分形维数、最大孔隙直径、气体的物理性质等对有效扩散系数均有显著影响。
(2)对比分形多孔介质气体扩散模型与Currie关于气体扩散率的数据发现:体孔隙度为0.10~ 0.65时,模型与多种不同的多孔介质实验数据均具有较好的一致性,说明该模型可以用于计算具有分形特性的多孔介质的气体有效扩散系数,对非常规天然气在实际多孔介质中的有效扩散系数的计算具有一定的参考意义。同时也能为后续研究多孔介质气液两相或多相渗透与扩散提供参考。
(3)考虑滑移因子的气体有效扩散系数大于未考虑滑移因子的气体有效扩散系数,在较小的孔隙直径下,两者的差距比较明显,随着孔隙直径的增大,两者的差异逐渐减小,直至相等。考虑了滑移因子的气体有效扩散系数与Currie关于气体扩散率的实验数据更加吻合。
| [1] |
郑仟. 分形多孔介质中气体流动与扩散的输运特性研究. 武汉: 华中科技大学物理系, 2012. ZHENG Q. Study of some transport properties for gas flow and diffusion through fractal porous media. Wuhan: Huazhong University of Science and Technology, 2012. |
| [2] |
CAO L Y, HE R. Gas diffusion in fractal porous media. Combustion Science and Technology, 2010, 182(7): 822-841. DOI:10.1080/00102200903341553 |
| [3] |
王晓琦, 翟增强, 金旭, 等. 页岩气及其吸附与扩散的研究进展. 化工学报, 2015, 66(8): 2838-2845. WANG X Q, ZHAI Z Q, JIN X, et al. Progress in adsorption and diffusion of shale gas. CIESC Journal, 2015, 66(8): 2838-2845. |
| [4] |
BESKOK A, KARNIADAKIS G E. A model for flows in channels, pipes, and ducts at micro and nano scales. Microscale Thermophysical Engineering, 1999, 3(1): 43-77. DOI:10.1080/108939599199864 |
| [5] |
符东宇, 李勇明, 赵金洲, 等. 基于REV尺度格子Boltzmann方法的页岩气藏渗流规律. 岩性油气藏, 2020, 32(5): 151-160. FU D Y, LI Y M, ZHAO J Z, et al. Gas seepage flow law of shale gas reservoirs based on REV-scale lattice Boltzmann method. Lithologic Reservoirs, 2020, 32(5): 151-160. |
| [6] |
ROY S, RAJU R. Modeling gas flow through microchannels and nanopores. Journal of Applied Physics, 2003, 93(8): 4870-4879. DOI:10.1063/1.1559936 |
| [7] |
张烈辉, 单保超, 赵玉龙, 等. 页岩气藏表观渗透率和综合渗流模型建立. 岩性油气藏, 2017, 29(6): 108-118. ZHANG L H, SHAN B C, ZHAO Y L, et al. Establishment of apparent permeability model and seepage flow model for shale reservoir. Lithologic Reservoirs, 2017, 29(6): 108-118. DOI:10.3969/j.issn.1673-8926.2017.06.014 |
| [8] |
李亚雄, 刘先贵, 胡志明, 等. 页岩气滑脱、扩散传输机理耦合新方法. 物理学报, 2017, 66(11): 230-240. LI Y X, LIU X G, HU Z M, et al. A new method for the transport mechanism coupling of shale gas slippage and diffusion. Acta Physica Sinica, 2017, 66(11): 230-240. |
| [9] |
陈居凯, 朱炎铭, 崔兆帮, 等. 川南龙马溪组页岩孔隙结构综合表征及其分形特征. 岩性油气藏, 2018, 30(1): 55-62. CHEN J K, ZHU Y M, CUI Z B, et al. Pore structure and fractal characteristics of Longmaxi shale in southern Sichuan Basin. Lithologic Reservoirs, 2018, 30(1): 55-62. DOI:10.3969/j.issn.1673-8926.2018.01.006 |
| [10] |
朱汉卿, 贾爱林, 位云生, 等. 基于氩气吸附的页岩纳米级孔隙结构特征. 岩性油气藏, 2018, 30(2): 77-84. ZHU H Q, JIA A L, WEI Y S, et al. Nanopore structure characteristics of shale based on Ar adsorption. Lithologic Reservoirs, 2018, 30(2): 77-84. |
| [11] |
邓浩阳, 司马立强, 吴玟, 等. 致密砂岩储层孔隙结构分形研究与渗透率计算: 以川西坳陷蓬莱镇组、沙溪庙组储层为例. 岩性油气藏, 2018, 30(6): 76-82. DENG H Y, SIMA L Q, WU W, et al. Fractal characteristics of pore structure and permeability calculation for tight sandstone reservoirs: A case of Penglaizhen Formation and Shaximiao Formation in western Sichuan Depression. Lithologic Reservoirs, 2018, 30(6): 76-82. |
| [12] |
姜瑞忠, 张春光, 郜益华, 等. 缝洞型碳酸盐岩油藏水平井分形非线性渗流. 岩性油气藏, 2019, 31(6): 118-126. JIANG R Z, ZHANG C G, GAO Y H, et al. Fractal nonlinear seepage model of horizontal wells in fractured-vuggy carbonate reservoirs. Lithologic Reservoirs, 2019, 31(6): 118-126. |
| [13] |
李玉丹, 董平川, 张荷, 等. 基于分形理论的页岩基质表观渗透率研究. 油气地质与采收率, 2017, 24(1): 92-99. LI Y D, DONG P C, ZHANG H, et al. Analysis on apparent permeability of shale matrix based on fractal theory. Petroleum Geology and Recovery Efficiency, 2017, 24(1): 92-99. |
| [14] |
王世芳, 吴涛, 曹秀英. 分形多孔材料的一种改进化气体扩散分形模型. 化学工程, 2018, 46(2): 14-17. WANG S F, WU T, CAO X Y. An improved gas diffusivity fractal model for fractal porous materials. Chemical Engineering(China), 2018, 46(2): 14-17. |
| [15] |
ZHENG Q, YU B M, WANG S F, et al. A diffusivity model for gas diffusion through fractal porous media. Chemical Engineering Science, 2012, 68(1): 650-655. |
| [16] |
SHI Y, XIAO J S, QUAN S H, et al. Fractal model for prediction of effective hydrogen diffusivity of gas diffusion layer in proton exchange membrane fuel cell. International Journal of Hydrogen Energy, 2009, 35(7): 2863-2867. |
| [17] |
ZHANG L Z. A fractal model for gas permeation through porous membranes. International Journal of Heat and Mass Transfer, 2008, 51(21): 5288-5295. |
| [18] |
WOIGNIER T, ANEZ L, CALAS-ETIENNE S, et al. Gas slippage in fractal porous material. Journal of Natural Gas Science and Engineering, 2018, 57: 11-20. |
| [19] |
张赛, 陈君若, 刘显茜. 气体有效扩散系数的分形模型. 化学工程, 2013, 41(5): 39-43. ZHANG S, CHEN J R, LIU X X. Fractal model of gas effective diffusivity. Chemical Engineering(China), 2013, 41(5): 39-43. |
| [20] |
牟新竹, 陈振乾. 多尺度分形多孔介质气体有效扩散系数的数学模型. 东南大学学报(自然科学版), 2019, 49(3): 520-526. MOU X Z, CHEN Z Q. Mathematical model for effective gas diffusion coefficient in multi-scale fractal porous media. Journal of Southeast University(Natural Science Edition), 2019, 49(3): 520-526. |
| [21] |
郁伯铭, 徐鹏, 邹明清, 等. 分形多孔介质输运物理. 北京: 科学出版社, 2014, 5-33. YU B M, XU P, ZOU M Q, et al. Transport physics in fractal porous media. Beijing: Science Press, 2014, 5-33. |
| [22] |
朱维耀, 马千, 邓佳, 等. 纳微米级孔隙气体流动数学模型及应用. 北京科技大学学报, 2014, 36(6): 709-715. ZHU W Y, MA Q, DENG J, et al. Mathematical model and application of gas flow in nano-micron pores. Journal of University of Science and Technology Beijing, 2014, 36(6): 709-715. |
| [23] |
刘圣鑫, 钟建华, 刘晓光, 等. 致密多孔介质气体运移机理. 天然气地球科学, 2014, 25(10): 1520-1528. LIU S X, ZHONG J H, LIU X G, et al. Gas transport mechanism in tight porous media. Natural Gas Geoscience, 2014, 25(10): 1520-1528. |
| [24] |
FENG Y J, YU B M, ZOU M Q, et al. A generalized model for the effective thermal conductivity of porous media based on selfsimilarity. Journal of Physics D: Applied Physics, 2004, 37: 3030-3040. |
| [25] |
尹帅, 谢润成, 丁文龙, 等. 常规及非常规储层岩石分形特征对渗透率的影响. 岩性油气藏, 2017, 29(4): 81-90. YIN S, XIE R C, DING W L, et al. Influences of fractal characteristics of reservoir rocks on permeability. Lithologic Reservoirs, 2017, 29(4): 81-90. |
| [26] |
CURRIE J A. Gaseous diffusion in porous media. Part 2:Dry granular materials. British Journal of Applied Physics, 1960, 11(8): 318-324. |
 2021, Vol. 33
2021, Vol. 33




