压裂液返排效率低是页岩气藏水力压裂的一大特点[1-3],滞留在页岩储层中的大量压裂液会提高裂缝面附近的含水饱和度,造成气流堵塞,气井产能下降。当含水饱和度在40%~50% 时,气井产能将会受到严重损害。大量研究表明[4-6],自发渗吸作用是造成压裂液在页岩储层中滞留的主要因素之一,而基质孔隙内的毛管压力作用则是主要驱动力,但在实验研究中发现化学渗透压也是影响自发渗吸效果的重要因素[7-8]。通常滑溜水压裂液的矿化度约为(1 000~5 000)×10-6,而页岩储层中原始地层水的矿化度可以高于210 000×10-6[9],两者之间矿化度的差异会导致大量压裂液在化学渗透压作用下自发渗吸进入页岩基质中,对压裂液返排效果产生巨大影响。Fakcharoenphol等[10]通过实验证实当页岩放置于低矿化度溶液中时,页岩会表现出半透膜的特性,在渗透压的作用下驱动低矿化度的水分子进入页岩孔隙中。Zhang等[11]则认为渗透压驱动的流动除与化学势有关外,还受半透膜两端分子浓度不平衡产生的扩散现象影响。Ge等[12]通过实验发现页岩在蒸馏水中的吸水总量高于在质量分数为10% 的KCl溶液中的吸水总量,间接证明了页岩内化学势的存在。
由于受到实验仪器和技术的限制,目前针对页岩渗吸的实验研究主要是通过测定页岩渗吸量与渗吸时间的关系,在此基础上来判别裂缝、黏土矿物和表面活性剂对渗吸效果的影响[13-15]。此外,实验结果与数值模拟也没能形成有效结合,在数值模拟中没有考虑化学渗透压对产量的影响,导致模拟结果缺乏准确性。因此,本文基于核磁共振测试原理,以鄂尔多斯盆地本溪组页岩为研究对象开展页岩自发渗吸实验,结合化学渗透压作用下的渗吸动力模型,分析黏土矿物、矿化度和表面活性剂对含水饱和度分布曲线的影响,并将拟合后的毛管压力曲线应用于页岩气井产量模型预测,以期提高模型的计算精度。
1 化学渗透压作用下渗吸动力模型多组分溶液体系中某一组分A的化学势微分方程可以表示为
| $ \mathrm{d} \mu_{\mathrm{A}}=-S_{\mathrm{Am}} \mathrm{d} T+V_{\mathrm{Am}} \mathrm{d} p $ | (1) |
式中:μA为A组分的化学势,kJ/mol;SAm为A组分的偏摩尔熵,kJ(/ mol·K);VAm为A组分的偏摩尔体积,m3/kmol;T为体系温度,K;p为体系压力,10-1 MPa。
在等温条件下,组分A的化学势可由式(1)积分得出
| $ \int_{P_{0}}^{p} \mathrm{~d} \mu_{\mathrm{A}}=\int_{P_{0}}^{p} V_{\mathrm{Am}} \mathrm{d} p $ | (2) |
即
| $ \mu_{\mathrm{A}}(T, p)=\mu_{\mathrm{A}}\left(T, p_{0}\right)+\int_{P_{0}}^{p} V_{\mathrm{Am}} \mathrm{~d} p $ | (3) |
式中:μA(T, p) 为溶液中A组分的化学势,kJ/mol;p0为标准大气压力,10-1 MPa;μA(T, p0) 为溶液中A组分的标准化学势,kJ/mol。
当溶液A为理想溶液时,组分A的化学势可以表示为
| $ \mu_{\mathrm{A}}(T, p)=\mu_{\mathrm{A}}^{*}(T, p)+R T \ln x_{\mathrm{A}} $ | (4) |
式中:μA* (T, p) 为纯溶液的化学势,kJ/mol;R为理想气体常数,0.008 314,kJ(/ mol·K);xA为溶液中A组分的摩尔分数。
在不同压力p1和p2下,2个含有不同浓度A组分(x1和x2)的溶液之间化学电位差为
| $ \mu_{\mathrm{A}}\left(T, p_{1}, x_{1}\right)-\mu_{\mathrm{A}}\left(T, p_{2}, x_{2}\right)=\mu_{\mathrm{A}}\left(T, p_{1}\right)+R T \ln x_{1}-\left[\mu_{\mathrm{A}}\left(T, p_{2}\right)+R T \ln x_{2}\right] $ | (5) |
将式(3),(5)合并可得
| $ \mu_{\mathrm{A}}\left(T, p_{1}, x_{1}\right)-\mu_{\mathrm{A}}\left(T, p_{2}, x_{2}\right)=\left[\mu_{\mathrm{A}}\left(T, p_{0}\right)+\int_{p_{0}}^{p_{1}} V_{\mathrm{B}} \mathrm{d} p\right]-\left[\mu_{\mathrm{A}}\left(T, p_{0}\right)+\int_{p_{0}}^{p_{2}} V_{\mathrm{B}} \mathrm{d} p\right]+R T \ln \frac{x_{1}}{x_{2}} $ | (6) |
上式整理后为
| $ \mu_{{\mathrm{A}}}\left(T, p_{1}, x_{1}\right)-\mu_{{\mathrm{A}}}\left(T, p_{2}, x_{2}\right)=\int_{p_{2}}^{p_{1}} V_{{\mathrm{A}}} \mathrm{~d} p+R T \ln \frac{x_{1}}{x_{2}} $ | (7) |
当偏摩尔分数不随压力变化时,不同浓度的2种溶液之间的化学电位差可写为
| $ \mu_{\mathrm{A}}\left(T, p_{1}, x_{1}\right)-\mu_{\mathrm{A}}\left(T, p_{2}, x_{2}\right)=V_{\mathrm{A}}\left(p_{1}-p_{2}\right)+R T \ln \frac{x_{1}}{x_{2}} $ | (8) |
当压裂液通过水力裂缝进入含有原始地层水的页岩基质时,原始地层水与压裂液的化学电位差可表示为
| $ \mu_{\mathrm{w}}^{\mathrm{f}}-\mu_{\mathrm{w}}^{\mathrm{m}}=V_{\mathrm{w}}\left(p_{\mathrm{w}}^{\mathrm{f}}-p_{\mathrm{w}}^{\mathrm{m}}\right)+R T \ln \frac{x_{\mathrm{f}}}{x_{\mathrm{m}}} $ | (9) |
式中:μwf和μwm分别为压裂液的化学势和基质中原始地层水的化学势,kJ/mol;Vw为水相的偏摩尔体积,m3/kmol;pwf和pwm分别为裂缝和基质中的孔隙压力,10-1 MPa;xf和xm分别为压裂液和原始地层水中水分子的摩尔分数,可以通过分析含盐溶液中矿物浓度计算得到。
式(9)又可以写成
| $ \frac{\mu_{\mathrm{w}}^{\mathrm{f}}-\mu_{\mathrm{w}}^{\mathrm{m}}}{V_{\mathrm{w}}}=p_{\mathrm{w}}^{\mathrm{f}}-p_{\mathrm{w}}^{\mathrm{m}}+\frac{R T}{V_{\mathrm{w}}} \ln \frac{x_{\mathrm{f}}}{x_{\mathrm{m}}} $ | (10) |
当忽略压裂液与原始地层水之间矿化度的差异时,驱动力μwf - μwm /Vw即等于水力压差pwf - pwm,式(10)变为常规黏性力方程。而页岩自发渗吸过程中,pwf - pwm为毛管压力。当考虑压裂液与基质中原始地层水之间矿化度的差异时,
| $ \frac{\mu_{\mathrm{w}}^{\mathrm{f}}-\mu_{\mathrm{w}}^{\mathrm{m}}}{V_{\mathrm{w}}}=p_{\mathrm{w}}^{\mathrm{f}}-p_{\mathrm{w}}^{\mathrm{m}}+\lambda \frac{R T}{V_{\mathrm{w}}} \ln \frac{x_{\mathrm{f}}}{x_{\mathrm{m}}} $ | (11) |
式中:λ为膜透过率,一般小于5%。
2 实验部分 2.1 核磁共振测试原理低场核磁共振技术是以流体中的氢原子核在磁场中的响应为基础,通过测量1H的横向弛豫时间T2来分析含氢流体在岩石孔隙结构中弛豫行为的技术[16-18]。在页岩和致密砂岩中,孔隙直径主要为微米和纳米级别,孔隙中流体的横向弛豫时间主要受岩石表面横向弛豫时间的控制,而受流体固有弛豫时间和扩散引起的弛豫时间影响较小。因此,在自发渗吸实验中,通过对渗吸后的岩心进行纵向切片式扫描后,可以获得此状态下岩心不同切片的信号强度值,该值与岩心完全饱和渗吸液后的基准信号强度值之比即为岩心不同切片的含水饱和度值,进而可以对岩心内部的含水饱和度分布进行研究。
2.2 实验材料实验中所用岩心来自鄂尔多斯盆地本溪组页岩取样井。通过X射线衍射实验和低压氮气吸附解吸实验获取实验岩心的基本物性参数(表 1-2),其中1#,3# 和4# 岩心来自于同一口井同一深度的岩样,2# 岩心来自邻近页岩气井的取样。实验岩心的平均渗透率为0.002 mD,平均有机碳质量分数为3.85%,矿物组成中以石英和黏土为主,其中2# 页岩的黏土质量分数达到45.7%,远高于其他页岩。
|
|
下载CSV 表 1 实验岩心基本参数 Table 1 Basic parameters of experimental cores |
|
|
下载CSV 表 2 实验岩心X射线衍射黏土矿物分析 Table 2 Clay minerals analysis by X-ray diffraction of experimental cores |
实验中所用渗吸液分别为去离子水、质量分数为15% 的KCl溶液和2.2% 的HYS-2非离子表面活性剂。其中去离子水的黏度为1.0 mPa·s,表面张力为72.1 mN/m;KCl溶液的黏度为0.8 mPa·s,表面张力为70.4 mN/m;HYS-2表面活性剂的黏度为1.2 mPa·s,表面张力为26.7 mN/m。
2.3 实验步骤① 将实验页岩岩心放置于120 ℃的恒温箱中烘干,直至岩心重量不再减小;②当岩心降至室温后,将对应编号的岩心放置于装有足够对应类型渗吸液的渗吸池中,采用挂绳将岩心竖直悬挂在渗吸池中央,并确保渗吸液刚好淹没岩心下端面(图 1);③每隔30 min对岩心进行一次核磁共振扫描(岩心水平放置,垂向切片式扫描,每次扫描用时3 min),以获取岩心在不同自发渗吸时间下的含水饱和度分布,扫描完成后立即将岩心放回原位,继续实验;④当连续3次扫描岩心含水饱和度信号强度不变时,自发渗吸实验结束。⑤采用高速离心机依次在5个离心压力(100 psi,200 psi,300 psi,400 psi和500 psi)下对岩心饱和渗吸液,随着离心力的增加,岩心中含水饱和度不再增大或增大幅度很小时,认为岩心完全饱和渗吸液,得到最佳饱和离心力为400 psi。当饱和完成后再次进行核磁共振扫描,直至3次扫描结果无变化。
|
下载原图 图 1 页岩自发渗吸实验示意图 Fig. 1 Schematic diagram of shale spontaneous imbibition experiment |
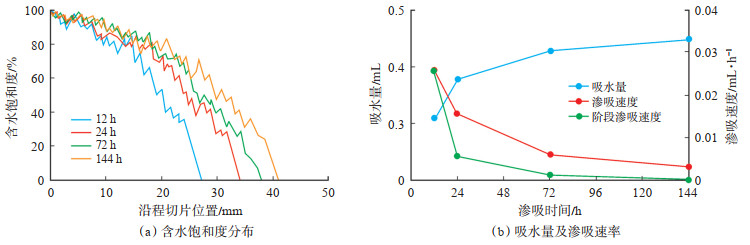
图 2(a)为1# 岩心在不同渗吸时间下沿程切片内含水饱和度分布的变化。从含水饱和度上下波动的递进式型态可以看出页岩内复杂的孔隙结构分布,由于受到不同毛管压力和盐离子浓度的影响,导致吸水剖面不连续也不均匀。渗吸前缘与渗吸面的距离随渗吸时间的增加而增大,但随着渗吸时间的增加,渗吸前缘距离增大的幅度在减小。当渗吸时间为12 h时,1# 岩心的渗吸前缘距离为27.1 mm;当渗吸时间达到144 h时,渗吸前缘距离为41.1 mm。
|
下载原图 图 2 1# 岩心含水饱和度分布和吸水量及渗吸速率 Fig. 2 Variation of water saturation distribution and imbibition velocity with imbibition time of shale 1# |
此外,根据不同时间下岩心沿程切片含水饱和度分布及渗吸距离可以计算出岩心在渗吸过程中的总吸水量、渗吸速率和阶段渗吸速率(2次扫描时间间隔内的渗吸速率)。由图 2(b)可知,在渗吸初期(渗吸时间为12 h),1# 岩心吸水量快速增加,达到0.31 mL,此时渗吸速率和阶段渗吸速率达到最大。随着渗吸时间的增加,虽然吸水量继续增加,但渗吸速率开始降低,阶段渗吸速率则由12 h测定的0.026 mL/h下降至24 h测定的0.005 mL/h,降低幅度达78.2%。当渗吸时间达到144 h时,阶段渗吸速率降至0.28×10-3 mL/h。由此可知,页岩的自发渗吸作用主要发生在与渗吸液接触后的初期,该时期内渗吸液在毛管压力和润湿性(相对气相、页岩亲水)的双重作用下,以孔壁表面水膜变厚的形式“快速”进入孔隙。随着渗吸液进入页岩内部深度的增加,渗吸速率快速下降。
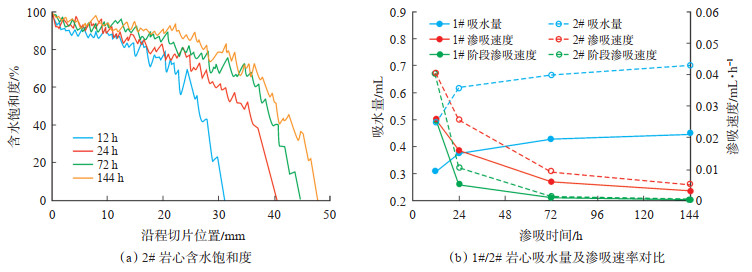
2.4.2 黏土矿物的影响在自发渗吸过程中,黏土矿物含量的高低会对渗吸效果产生较大影响。而页岩储层中黏土矿物含量一般远高于常规砂岩储层,导致其渗吸效果受黏土矿物含量的影响更大。图 3为高含黏土矿物页岩渗吸过程中含水饱和度分布、吸水量和渗吸速率的变化特征。从图 3(a)可以看出,相比于1# 岩心,2# 岩心在同等渗吸时间下的渗吸前缘距离更大,当渗吸时间达到144 h时,2#岩心的渗吸前缘距离达到47.5 mm,且渗吸剖面相对平缓。由图 3(b)可知,2# 岩心渗吸速率和阶段渗吸速率均随渗吸时间的增加而减小,变化趋势与1# 岩心相似,但2# 岩心的吸水量0.699 mL高于1# 岩心的0.448 mL。根据X射线衍射实验结果(参见表 2)可知,2# 岩心的黏土矿物质量分数为45.7%,远高于1# 岩心黏土矿物质量分数33.8%。其中,2# 岩心中伊/蒙混层占比达到了51.3%,当伊/蒙混层矿物与水作用后,会迅速膨胀变大,其体积可以膨胀至原体积的6~8倍,导致岩心中大量微裂缝的产生,增大岩心渗透率的同时提高了渗吸速率。此外,结合式(11)可知,岩心中具有较高的黏土矿物含量会造成页岩颗粒的比表面积大幅增加,一方面会导致毛管压力的增加,另一方面会使膜效率λ更大,共同导致驱动力项的增大,进而提高渗吸前缘距离和吸水量。
|
下载原图 图 3 高含黏土矿物页岩含水饱和度分布和吸水量及渗吸速率对比 Fig. 3 Variation of water saturation distribution and imbibition velocity with imbibition time of shale 2# |
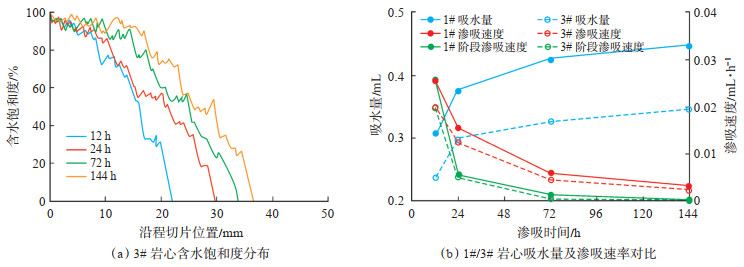
通常,页岩储层中的原始地层水具有较高的矿化度,当与低矿化度的压裂液相接触时,会因为化学势差产生自发渗吸作用。图 4为高矿化度(质量浓度为15% 的KCl)渗吸液作用下3# 岩心渗吸过程中含水饱和度、吸水量和渗吸速率的变化特征。由图 4(a)可知,在相同渗吸时间下,3# 岩心的渗吸前缘距离小于1# 岩心,且其渗吸剖面的变化也更陡。当渗吸时间达到144 h时,3# 岩心的渗吸前缘距离仅为36.5 mm,远小于1# 岩心的渗吸前缘距离41.1 mm。从阶段渗吸速率[图 4(b)]可以看出,在渗吸初期(24 h内),1# 和3# 岩心的阶段渗吸速率存在较大差异,1# 岩心的阶段渗吸速率较大,但随着渗吸时间的增加,两者之差快速变小,这主要是因为1#岩心所用的渗吸液为去离子水,而3# 岩心所用渗吸液为KCl溶液,导致1# 岩心基质内的原始矿化度与渗吸液之间形成的化学势差大于3#岩心的化学势差。在1# 和3# 岩心储层物性和矿物含量基本相同(参见表 1-2)的情况下,化学势差越大表明渗吸动力越强,渗吸速率也越大,但随着渗吸时间的增加,1# 岩心的化学势差也在迅速降低,导致其渗吸速率与3# 岩心逐渐一致。
|
下载原图 图 4 高矿化度渗吸液作用下含水饱和度分布和吸水量及渗吸速率对比 Fig. 4 Variation of water saturation distribution and imbibition velocity with imbibition time of shale 3# |
图 5为质量分数为2.2% 的HYS-2非离子表面活性剂作用下4#页岩渗吸过程中含水饱和度、吸水量和渗吸速率的变化特征。由图 5(a)可以看出,在HYS-2表面活性剂作用下,4# 页岩的渗吸前缘距离仅有36.4 mm,最大渗吸水量为0.372 mL,均低于1# 页岩。这主要是因为在压裂液中添加HYS-2表面活性剂后,压裂液的表面张力明显下降,由原来的72.1 mN/m降至26.7 mN/m,与页岩颗粒表面的接触角由原来的35.5°增加至92°,导致毛管压力大幅降低。结合式(11)可知,毛管压力的降低引起驱动力的下降,导致渗吸前缘距离减小,渗吸效果大幅减弱。此外,从1# 和4# 页岩阶段渗吸速率的变化趋势[图 5(b)]可以看出,在渗吸初期(12 h内),阶段渗吸速率1# 页岩的(0.026 mL/h)大于4# 页岩(0.021 mL/h),但随着渗吸时间的增加,4# 页岩与1# 页岩的渗吸速率逐渐趋于一致,说明压裂液中添加表面活性剂的作用随着渗吸时间的增加而减弱,这主要是页岩中基质与裂缝间矿化度差异的存在,导致矿化度差异引发的化学势差对渗吸的影响大于表面活性剂作用下对渗吸的影响,使得2块页岩的渗吸速率逐渐趋于一致。
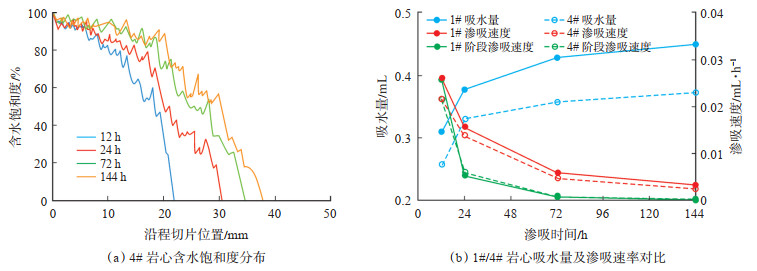
|
下载原图 图 5 表面活性剂作用下含水饱和度分布和渗吸速率随渗吸时间的变化 Fig. 5 Variation of water saturation distribution and imbibition velocity with imbibition time of shale 4# |
目前市面上的商业数值模拟软件均未考虑化学渗透压对页岩自发渗吸的影响,导致模拟的结果与实际情况存在较大差异[19-20]。基于以上实验结果,可以将测得的含水饱和度分布曲线用来拟合页岩储层的毛管压力曲线,使得拟合后的毛管压力同时具有毛管压力和化学渗透压的双重作用。
采用CMG模拟器的IMEX模块,以水平长度为600 m的某页岩气储层水平井为模拟对象。采用三级水力压裂工艺对该井实行分段多簇水力压裂,在每个单级中,沿水平井眼形成3个横向裂缝,每段内裂缝间距30 m,每个裂缝的裂缝半长为180 m。页岩储层的厚度、长度和宽度分别为45 m,1 400 m和600 m。储层、流体和裂缝的基本性质如表 3所列。
|
|
下载CSV 表 3 数值模拟中储层、流体和裂缝的基本参数 Table 3 Basic parameters of reservoir, fluid and fracture in numerical simulation |
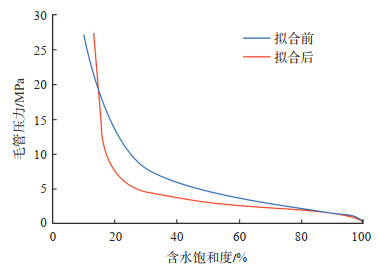
在开展数值模拟前,首先通过高压压汞测试获取目标储层的毛管压力曲线,然后根据式(12)将汞饱和度下的毛管压力曲线转换为气水两相下的毛管压力曲线(图 6中蓝线)
| $ P_{\mathrm{wg}}=\frac{\sigma_{\mathrm{wg}} \cos \theta_{\mathrm{wg}}}{\sigma_{\mathrm{Hg}} \cos \theta_{\mathrm{Hg}}} P_{\mathrm{Hg}} $ | (12) |
|
下载原图 图 6 拟合前后毛管压力曲线对比 Fig. 6 Comparison of capillary pressure curves before and after fitting |
式中:PHg为汞饱和度下的毛管压力,MPa;Pwg为水饱和度下的毛管压力,MPa;σwg为气水界面张力,mN/m;σHg为汞界面张力,mN/m;θwg为气水接触角,(°);θHg为汞接触角,(°)。
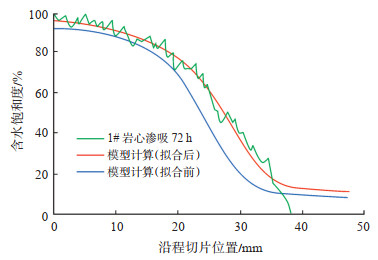
根据实验岩心的基本物性参数建立岩心尺度的数值模型,通过将模拟计算的结果与实验测定的含水饱和度分布曲线进行拟合(图 7),可以获取一条兼具毛管压力和化学渗透压双重作用的毛管压力曲线(图 6中红线)。将拟合后的毛管压力曲线带入页岩储层尺度的数值模型中进行计算,可以提高模型精度。
|
下载原图 图 7 (未)拟合毛管压力曲线模型计算出的含水饱和度分布与1#岩心渗吸实验拟合结果对比 Fig. 7 Fitting result of water saturation distribution by model calculation and imbibition experiment of shale 1# |
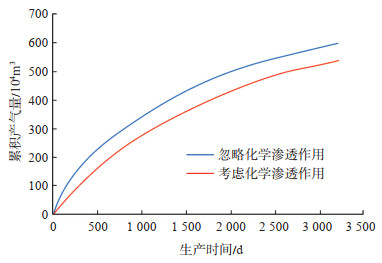
图 8为采用拟合后的毛管压力曲线(考虑化学渗透压)与未拟合毛管压力曲线计算出的累积产气量的对比。由图可以看出,2条累积产气量曲线随时间的变化趋势基本一致,但在同一生产时间下,考虑化学渗透压计算出来的累积产气量小于未考虑化学渗透压下的计算值,且两者之差最大可达10.7%。这主要是在化学渗透压作用下会有更多压裂液滞留在储层中,造成裂缝面附近含水饱和度上升,堵塞气流通道,导致压裂后产能降低。由此可以看出,如果采用未修正的毛管压力曲线进行产量预测,得到的结果势必与实际生产情况有较大差异。因此,在矿场实际应用中应采用考虑化学渗透压作用下的毛管压力曲线,以获取更高的模拟精度。
|
下载原图 图 8 考虑化学渗透压与忽略化学渗透压下累积产气量对比 Fig. 8 Comparison of cumulative gas production with and without chemical osmotic pressure |
(1)在压裂过程中,当忽略压裂液与原始地层水之间矿化度的差异时,压裂液进入基质的动力仅为水力压差,而页岩自发渗吸过程中,考虑压裂液与原始地层水之间矿化度的差异时,驱动力为水力压差与渗透压之和。
(2)页岩在自发渗吸过程中,吸水量与渗吸时间呈现出先快速增加后逐渐变缓的趋势,而渗吸速率则随着时间的增加而快速下降。黏土矿物含量越高、基质内外化学势差越大,渗吸驱动力越强,渗吸前缘距离和吸水量越大;表面活性剂的存在会降低毛管压力,引起驱动力下降,导致渗吸效果大幅减弱。
(3)考虑化学渗透压作用下的累积产气量小于忽略化学渗透压作用下的计算值,两者之差最大可达10.7%,在矿场实际应用中应采用考虑化学渗透压作用下的毛管压力曲线,以获取更高的模拟精度。
| [1] |
罗群, 吴安彬, 王井伶, 等. 中国北方页岩气成因类型、成气模式与勘探方向. 岩性油气藏, 2019, 31(1): 1-11. LUO Q, WU A B, WANG J L, et al. Genetic types, generation models, and exploration direction of shale gas in northern China. Lithologic Reservoirs, 2019, 31(1): 1-11. |
| [2] |
邹才能, 董大忠, 王玉满, 等. 中国页岩气特征、挑战及前景(二). 石油勘探与开发, 2016, 43(2): 166-178. ZOU C N, DONG D Z, WANG Y M, et al. Shale gas in China: Characteristics, challenges and prospects(Ⅱ). Petroleum Exploration and Development, 2016, 43(2): 166-178. |
| [3] |
杜洋, 雷炜, 李莉, 等. 页岩气井压裂后焖排模式. 岩性油气藏, 2019, 31(3): 145-151. DU Y, LEI W, LI L, et al. Shut-in and flow-back pattern of fractured shale gas wells. Lithologic Reservoirs, 2019, 31(3): 145-151. |
| [4] |
任岚, 邸云婷, 赵金洲, 等. 页岩气藏压裂液返排理论与技术研究进展. 大庆石油地质与开发, 2019, 38(2): 144-152. REN L, DI Y T, ZHAO J Z, et al. Advances in the theory and technique of the fracturing fluid flowback in shale gas reservoirs. Petroleum Geology and Oilfield Development in Daqing, 2019, 38(2): 144-152. |
| [5] |
LIN H, ZHANG S C, WANG F, et al. Experimental investigation on imbibition-front progression in shale based on nuclear magnetic resonance. Energy & Fuels, 2016, 30(11): 9097-9105. |
| [6] |
LUTZ B D, LEWIS A N, DOYLE M W. Generation, transport, and disposal of water associated with Marcellus shale gas development. Water Resources Research, 2013, 49(2): 647-656. DOI:10.1002/wrcr.20096 |
| [7] |
陈守雨, 修书志, 宋博, 等. 页岩气井压后返排动态模拟研究. 中外能源, 2016, 21(7): 43-50. CHEN S Y, XIU S Z, SONG B, et al. Research on dynamic simulation of fracturing fluid flowback in shale gas wells. Sino-Global Energy, 2016, 21(7): 43-50. |
| [8] |
DEHGHANPOUR H, ZUBAIR H A, CHHABRAA, et al. Liquid intake of organic shales. Energy & Fuels, 2012, 26(9): 5750-5758. |
| [9] |
KURTOGLU B. Integrated reservoir characterization and modeling in support of enhanced oil recovery for Bakken. Dissertations & Theses-Gradworks, 2013, 8: 1505-1508. |
| [10] |
FAKCHAROENPHOL P, KAZEMI H, CHAROENWONGSA S, et al. The effect of osmotic pressure on improve oil recovery from fractured shale formations. SPE Unconventional resource conference, 2014. |
| [11] |
ZHANG J, CHENEVERT M E, AL-BAZALI T, et al. A new gravimetric-swelling test for evaluating water and ion uptake in shales. SPE 89831, 2004.
|
| [12] |
GE H, YANG L, SHEN Y, et al. Experimental investigation of shale imbibition capacity and the factors influencing loss of hydraulic fracturing fluids. Petroleum Science, 2015, 12(4): 636-650. |
| [13] |
杨柳, 冷润熙, 常天全, 等. 页岩气储层渗吸与盐离子扩散相关关系. 中国海上油气, 2020, 32(2): 112-119. YANG L, LENG R X, CHANG T Q, et al. Correlation between the imbibition and salt ion diffusion of shale gas reservoirs. China Offshore Oil and Gas, 2020, 32(2): 112-119. |
| [14] |
林魂. 页岩气储层压后返排评估研究. 北京: 中国石油大学(北京), 2017. LIN H. Research on post-frac flowback of shale gas reservoir. Beijing: China University of Petroleum(Beijing), 2017. |
| [15] |
刘秀婵, 陈西泮, 刘伟, 等. 致密砂岩油藏东阳台渗吸驱油效果影响因素及应用. 岩性油气藏, 2019, 31(5): 114-120. LIU X C, CHEN X P, LIU W, et al. Influencing factors of dynamic imbibition displacement effect in tight sandstone reservoir and application. Lithologic Reservoirs, 2019, 31(5): 114-120. |
| [16] |
黄睿哲, 姜振学, 高之业, 等. 页岩储层组构特征对自发渗吸的影响. 油气地质与采收率, 2017, 24(01): 111-115. HUANG R Z, JIANG Z X, GAO Z Y, et al. Effect of composition and structural characteristics on spontaneous imbibition of shale reservoir. Petroleum Geology and Recovery Efficiency, 2017, 24(1): 111-115. |
| [17] |
王飞, 潘子晴. 化学势差驱动下的页岩储集层压裂液返排数值模拟. 石油勘探与开发, 2016, 43(6): 971-977. WANG F, PAN Z Q. Numerical simulation of chemical potential dominated fracturing fluid flowback in hydraulically fractured shale gas reservoirs. Petroleum Exploration and Development, 2016, 43(6): 971-977. |
| [18] |
ENGELDER T, CATHLES L M, BRYNDZIA L T. The fate of residual treatment water in gas shale. Journal of Unconventional Oil & Gas Resources, 2014, 7(3): 33-48. |
| [19] |
雷征东, 覃斌, 刘双双, 等. 页岩气藏水力压裂渗吸机理数值模拟研究. 西南石油大学学报(自然科学版), 2017, 39(2): 118-124. LEI Z D, QIN B, LIU S S, et al. Imbibition mechanism of hydraulic fracturing in shale gas reservoir. Journal of Southwest Petroleum University(Science & Technology Edition), 2017, 39(2): 118-124. |
| [20] |
张涛, 李相方, 王永辉, 等. 页岩储层特殊性质对压裂液返排率和产能的影响. 天然气地球科学, 2017, 28(6): 828-838. ZHANG T, LI X F, WANG Y H, et al. Study on the effect of gas shale reservoir special properties on the fracturing fluid recovery efficiency and production performance. Natural Gas Geoscience, 2017, 28(6): 828-838. |
 2021, Vol. 33
2021, Vol. 33



