2. 中国石化西北油田分公司完井测试管理中心, 新疆 轮台 841600;
3. 中国石油勘探开发研究院 西北分院, 兰州 730020
2. Completion and Well Test Management Center, Sinopec Northwest Oilfield Company, Luntai 841600, Xinjiang, China;
3. PetroChina Research Institute of Petroleum Exploration & Development-Northwest, Lanzhou 730020, China
多数油气藏储层岩石已完成压实和胶结,开采过程中,孔隙压力下降,岩石被压缩,以弹性变形为主,目前的研究认为孔隙度随应力变化的程度较小[1-4]。储层孔隙度是储量评价的重要参数[5-9],为了研究油藏孔隙度随应力的变化程度,大量实验表明在10~30 MPa的围压条件下,油藏岩石的孔隙度变化幅度在5%~40%[10-12]。储量评价研究中,也通常采用加载围压的实验测试方法对孔隙度进行校正[13]。
岩石本体变形的假设条件认为骨架颗粒压缩过程中保持形状不变,骨架与孔隙等比例变形。因此,岩石压缩过程中,骨架颗粒的排列形式和粒径分布均没有改变,变形过程中遵循孔隙度不变的原则[14-15],然而,真实条件下岩石骨架颗粒之间相互接触,颗粒的变形受到邻近颗粒的约束,压缩过程中骨架颗粒的形状会发生改变,并不严格遵守等比例变形的假设。为探索这一假设条件的合理性,本文通过有限元数值模拟方法,分析岩石本体变形中骨架颗粒的变形方式及其对孔隙度变化的影响机制,以期更好地指导油藏开发。
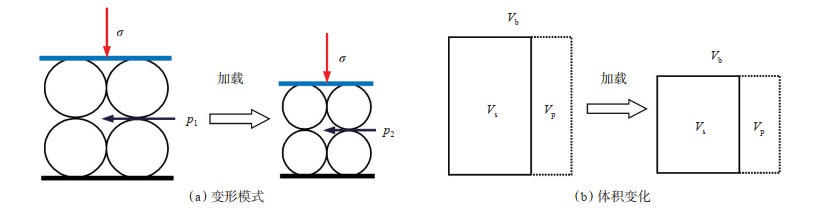
1 本体变形油藏岩石通常受上覆压力(外应力,σ)和孔隙压力(内应力,p)的共同作用(图 1)。油藏开采过程中,孔隙压力降低,岩石的骨架颗粒发生变形,导致岩石被压缩[16-17]。岩石存在本体变形和结构变形2种基本的变形机制[18]。本体变形中,骨架颗粒的形状和排列方式均不发生变化,变化的是骨架颗粒自身的体积[图 1(a)]。岩石的结构变形通常伴随本体变形,而在砂岩油藏(非裂缝性多孔介质)生产过程中,流体压力下降通常仅能引起岩石的本体变形。
|
下载原图 图 1 岩石的本体变形 Fig. 1 Primary deformation of reservoir rock |
岩石的孔隙度与骨架颗粒的大小无关,与骨架颗粒的排列方式与粒径分布有关[19]。孔隙是多孔介质的存在形式,而不是一种物质,孔隙的变化是骨架变化的结果。应力状态的变化,不能直接作用于岩石的孔隙,而是通过岩石骨架颗粒的变形引发孔隙的变形。本体变形中,仅有骨架颗粒的体积发生了变化,颗粒的形状和排列方式均未发生变化。因此,岩石的孔隙度并不发生变化[图 1(b)][20-21]。
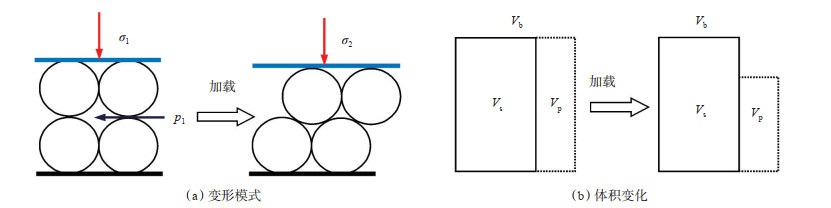
岩石的结构变形中,骨架颗粒自身的体积不发生变化,但颗粒的排列方式发生了变化(图 2),因此孔隙度会发生较大变化[图 2(b)]。结构变形实际上就是岩石的压实或微观破坏,通常发生在疏松多孔介质中(未胶结岩石)。致密介质则以本体变形为主,疏松介质以结构变形为主。
|
下载原图 图 2 岩石的结构变形 Fig. 2 Structural deformation of reservoir rock |
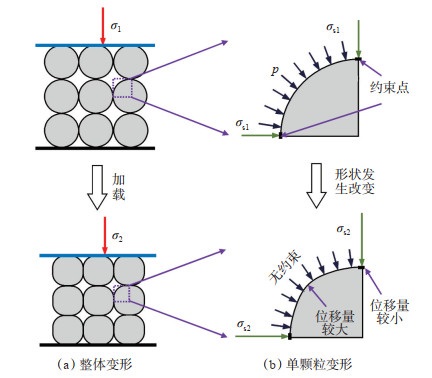
岩石本体变形推导过程中要求孔隙度保持不变,其中一个隐藏的假设条件是骨架颗粒的形状保持不变,即每个骨架颗粒独立发生压缩[参见图 1(a)],然而,真实情况下,多孔介质中的骨架颗粒之间相互接触,应力变化通过骨架颗粒的接触传递,这种接触对骨架颗粒的变形存在一定的约束。因此,多孔介质中骨架颗粒的变形,实质上是一种有约束的变形(图 3)。由于岩石已经胶结,骨架颗粒的排列方式一般难以发生变化,但压缩过程中,颗粒的形状发生一定的变化。
|
下载原图 图 3 骨架颗粒形状变化示意图 Fig. 3 Sketch diagram of skeleton particle deformation |
骨架颗粒在接触位置受到邻近颗粒的约束,而孔隙位置均匀地受到流体压力的约束[图 3(b)]。加载过程中,骨架应力σs增大,而孔隙压力不变或变化量较小。由于骨架颗粒受流体压力的作用是均匀的,因此孔隙位置可以认为不存在变形的约束条件。变形过程中,在约束位置(接触位置),骨架颗粒的弹性变形量会减小,而在无约束的位置(孔隙),弹性变形量会增加[图 3(b)]。因此,有约束的弹性变形从一定程度上也改变了骨架颗粒的形状,从而破坏了等比例变形的假设条件。约束变形条件下,骨架颗粒的变形量取决于骨架颗粒的弹性模型Es和泊松比μ。弹性模量决定颗粒弹性变形的程度,而泊松比决定骨架颗粒向“孔隙”方向的变形程度。这种有约束的变形一定程度上改变了骨架颗粒的形状,对孔隙度有一定的影响。
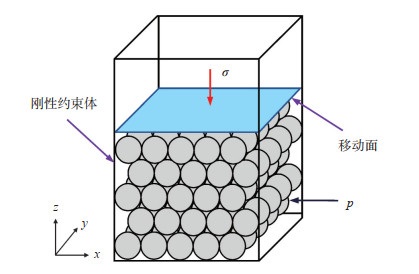
2.2 机理模型为研究约束变形对孔隙度的影响程度,探索本体变形假设条件的合理性,本文建立了颗粒数量n = 1×1×1,10×10×10和30×30×30的3种排列方式的骨架颗粒变形模型(图 4)。图 4中,骨架颗粒位于刚性约束体内,呈紧密排列;蓝色平面为移动面,通过蓝色平面的向下移动向骨架颗粒加载外应力(上覆压力)。
|
下载原图 图 4 骨架颗粒变形模型 Fig. 4 Deformation model of rock skeleton particles |
模型中,力学本构方程为弹性应力应变模型[22]。边界条件为蓝色平面会发生位移,但不出现变形,为刚性接触面,位移表现在颗粒压缩过程中会整体向下移动,而刚性约束体则既不发生位移,也不发生变形。
多孔介质和刚性约束体之间的接触面共同组成了数值实验中的表皮。数值实验的结果是多孔介质本身和表皮特性的共同表现,表皮对多孔介质本身性质的测试结果具有一定的影响(表皮效应)。在多孔介质内部,1个骨架颗粒与附近12个颗粒相邻,存在12个约束位置,而表皮上的骨架颗粒,约束位置数量明显减小(最少为6个)。因此,表皮上的骨架颗粒与多孔介质内部的约束不同。由于约束壁面不发生变形和位移,数值实验中的表皮为刚性表皮,仅有颗粒的变形方式发生变化。
通过单个颗粒的模拟研究不同材料的变形能力以及不同约束条件下的变形程度;通过单个颗粒和多个颗粒模型的对比研究颗粒接触约束面的数量对孔隙度降低的影响;通过10×10×10和30×30×30的模拟研究连续多孔介质的孔隙度变化特征以及表皮效应的作用。
由于解析方法难以直接计算颗粒的约束变形,本文基于有限元方法,通过ABAQUS软件进行模拟计算,颗粒的粒径设置为1 mm。模拟过程中,考虑到收敛速度,颗粒间的孔隙压力为2 MPa且保持不变,上覆压力σ的初始值为5 MPa,逐渐加载为10 MPa,20 MPa,40 MPa和60 MPa。为了反映骨架颗粒的变形特点,模拟了表 1中3种材料的单个骨架颗粒变形行为。在10×10×10和30×30×30共2种排列的模型中,模拟了软矿物(黏土)和硬矿物(石英)的变形特征。
|
|
下载CSV 表 1 3种材料的力学参数 Table 1 Mechanical parameters of three kinds of materials |
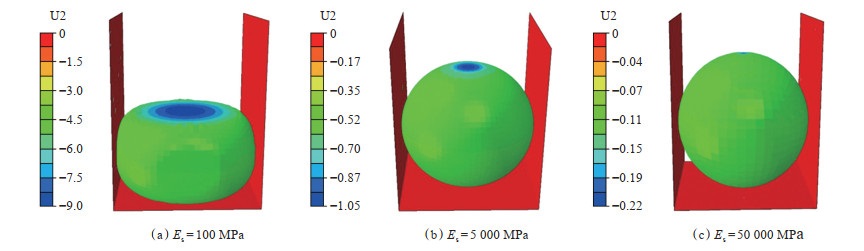
图 5为1个骨架颗粒在上覆压力60 MPa条件下的变形情况。其中,U代表每个网格单元的位移,而U2代表网格的中心在z轴方向(垂向)的位移(变形量,单位mm,球体半径为10 mm),正值代表向z轴正方向发生位移,负值代表向负方向发生位移。对于橡胶材料(Es=100 MPa),骨架颗粒的横向变形较为明显,此时骨架颗粒仅有6个接触约束位置[图 5(a)]。此时应力并没有达到骨架颗粒的屈服强度,骨架颗粒依旧处于弹性变化阶段,但是骨架颗粒的形状已经改变,不服从等比例变形的假设[图 5(a)],但是,对于黏土和石英矿物构成的骨架颗粒,骨架颗粒几乎没有发生变形。在60 MPa的上覆压力加载条件下,骨架颗粒依然保持了原来的形状,可以认为服从等比例变形的假设[图 5(a)]。
|
下载原图 图 5 上覆压力60 MPa条件下3种材料的有约束变形 Fig. 5 Deformation of three kinds of materials with constraint when σ = 60 MPa |
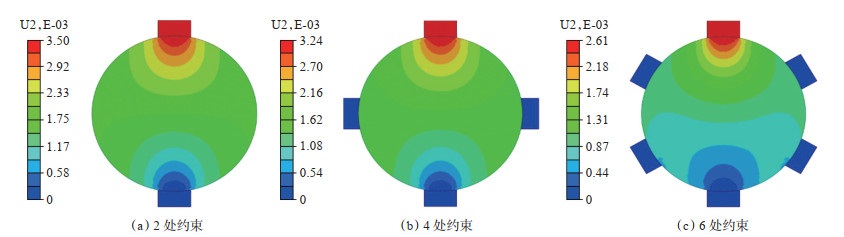
图 6显示了二维条件下石英颗粒(Es= 5 000 MPa)在60 MPa外应力条件下的约束变形情况,约束位置为面接触,接触圆半径为球体半径的10%。由于杨氏模量较大,石英颗粒在60 MPa外应力条件下的变形极为有限。当约束位置增多时,颗粒的变形受到明显的限制,变形量减小(图 6)。约束位置越多,颗粒的变形量越小颗粒的形状也几乎保持不变。当约束位置为6时,颗粒的变形更加类似于无约束条件下的变形特征,基本保持球体特性不变,而紧密排列的多孔介质内部,每个骨架颗粒的接触位置(约束位置)为12,因此颗粒变形方式更加接近本体变形的假设条件。
|
下载原图 图 6 不同约束条件下骨架颗粒的变形 Fig. 6 Deformation of skeleton particles under different constraint conditions |
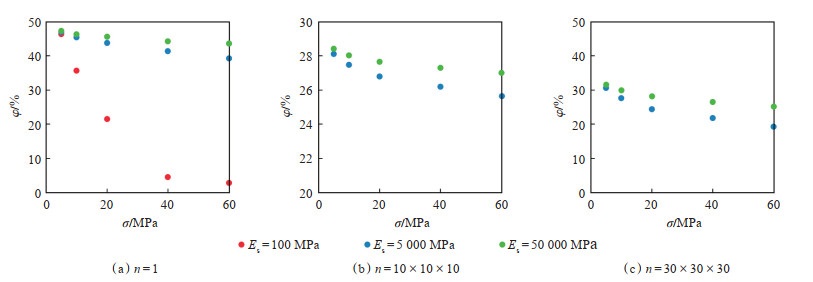
根据[图 7(a)],对于橡胶材料,由于变形能力较强,当上覆压力由5 MPa加载到60 MPa时,孔隙度从46.42% 变化为2.749%,软矿物颗粒(黏土)的孔隙度从46.86%变化为43.89%[图 7(a)],而硬矿物颗粒(石英)的孔隙度仅从47.23% 变化为46.64% [图 7(a)]。球体紧密排列条件下,多孔介质孔隙度的理论值为25.95%,但是数值实验中,多孔介质在刚性壁面上每1行都存在空缺,即表皮效应(参见图 3),孔隙度的初始值均大于理论值[图 7(b)]和[图 7(c)]。当n = 10×10×10时[图 6(b)],上覆压力由5 MPa增加至60 MPa,软矿物颗粒(黏土)的孔隙度从28.12% 减小到25.65%,而硬矿物颗粒的(石英)孔隙度从28.42%减小到27.00%[图 6(b)],硬矿物颗粒的孔隙度降低幅明显小于软矿物颗粒。
|
下载原图 图 7 上覆压力加载过程中的孔隙度变化 Fig. 7 Porosity change during overburden stress loading |
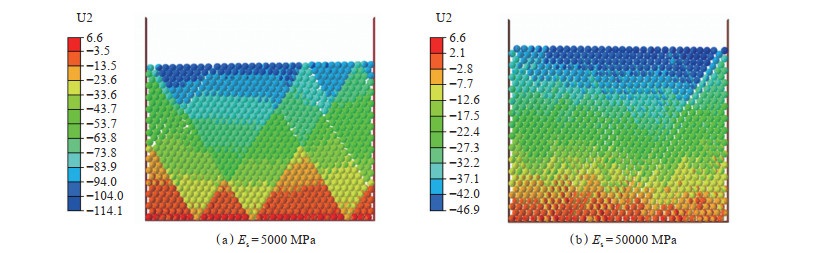
对于n = 30×30×30的骨架颗粒模型,孔隙度的变化趋势和特征与n=10×10×10的骨架颗粒加载模型一致[图 7(c)],但是,n = 30×30×30的骨架颗粒模型初始孔隙小于n=10×10×10的骨架颗粒模型,更加接近25.95% 的理论值。这是由于颗粒数量的增加削弱了接触面的表皮效应。根据n = 30×30×30的骨架颗粒模型的位移(图 8)可知,60 MPa的上覆压力条件下,由于软矿物的弹性模量较小,因此骨架颗粒的变形量明显大于硬矿物颗粒。2种材料的杨氏模型相差10倍,但是压缩过程中的位移量仅不到2倍的差距。根据[图 7(c)],对于黏土颗粒,当上覆压力由5 MPa增加至60 MPa时,孔隙度从26.12% 减小到23.86%;对于石英颗粒,孔隙度从26.32%减小到25.04%,2种材料的孔隙度减小量相差不大。
|
下载原图 图 8 上覆压力60 MPa条件下的颗粒位移 Fig. 8 Displacement of particles under overburden stress=60 MPa |
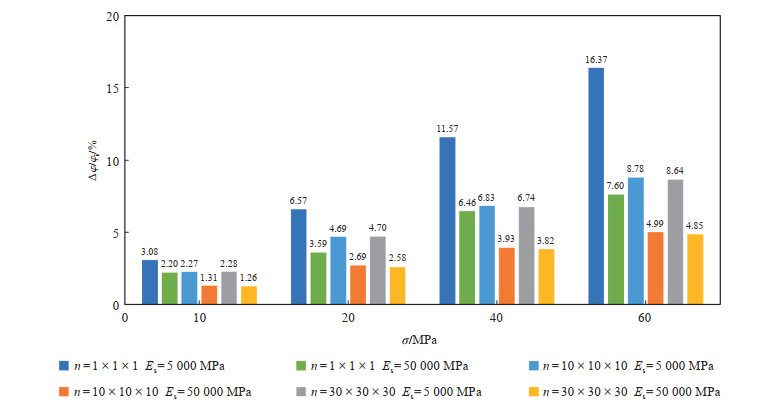
为表征孔隙度在加载过程中的下降程度,定义孔隙度损失率为孔隙度减小量与初始孔隙度的比值。根据孔隙度变化曲线(参见图 7),可以计算孔隙度损失率(图 9)。由图 9可知,当上覆压力增大时,孔隙度损失率不断变大。对于单个骨架颗粒的模型,孔隙度损失率较高。这是由于单个颗粒只有6个接触约束位置,而连续多孔介质中的多数骨架颗粒由12个约束接触位置,更多的约束位置限制了骨架颗粒的“横向变形”,从而减小了孔隙度的变化程度。对于n = 10×10×10和n = 30×30×30的多孔介质模型,骨架颗粒力学性质相近,则孔隙度损失率基本相同(图 9),硬矿物(石英)的孔隙度损失率明显小于软矿物(黏土)。当上覆压力由10 MPa加载到60 MPa时,硬矿物和软矿物(n = 30×30×30)的孔隙度损失率分别由1.26% 和2.28%,增加到4.85% 和8.64%。
|
下载原图 图 9 数值实验中的孔隙度损失率 Fig. 9 Porosity reduction ratio in numerical simulation |
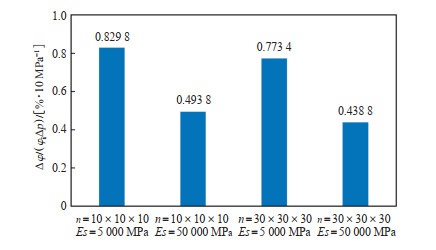
油藏开发过程中,上覆压力通常不变,而孔隙压力不断降低,由多孔介质有效应力原理可知,外应力(上覆压力)对骨架变形的作用效果远远高于孔隙压力的作用效果。油藏工程计算过程中,通常取10 MPa的孔隙压力变化量作为标准,为表征孔隙压力下降对孔隙度的影响程度,定义孔隙度的应力敏感指数为10 MPa内压变化条件下的孔隙度损失率。通过双重有效应力中的本体有效应力公式[14],可以将外应力的变化转换为孔隙压力的变化。选择σ=5 MPa到σ=20 MPa之间的加载过程,等效计算孔隙压力变化量,可以得到孔隙度应力敏感指数(图 10)。
|
下载原图 图 10 数值实验中的孔隙度应力敏感指数 Fig. 10 Stress sensitivity index of porosity in numerical simulation |
根据图 10可知,孔隙度应力敏感指数在10-3的数量级,这意味着孔隙压力下降10 MPa对孔隙度的影响较小。对于软矿物(n=30×30×30)而言,孔隙度应力敏感指数为0.7733%。如果初始孔隙度为15%,孔隙压力下降10 MPa,那么孔隙度由15.00% 降低为14.88%,降低值为0.12%;对于硬矿物(石英),10 MPa孔隙压降的孔隙度变化率仅为0.4388%;如果初始孔隙度为15%,孔隙度由15%降低为14.93%,降低值为0.07%。这种降低幅度已经远远超过了目前测量设备的最小精度。理论上,常规的孔隙度测试仪器难以准确获得10 MPa孔隙压力变化导致的孔隙度变化量。
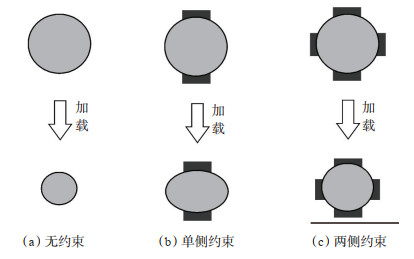
根据单个颗粒在约束条件下的变形模拟(参见图 6),图 11表现了颗粒受不同限制条件下的变形方式。[图 11(a)—(c)]分布表示颗粒的无约束变形、单侧约束和两侧应变约束条件下的变形示意图。根据图 11可知颗粒在受到限制的方向上没有产生变形,而在没有受到限制的方向上产生了较大的变形。当颗粒受限位置增多时,颗粒的变形反而更加类似于无约束条件下的变形特征,变形对孔隙度的影响也进一步降低。
|
下载原图 图 11 不同约束条件下的变形示意图 Fig. 11 Sketch map of deformation under different constraint conditions |
本文机理模型中的单个颗粒具有6个接触约束面,连续多孔介质的中间颗粒具有12个接触约束面。对于真实岩石骨架颗粒,粒径分布更为复杂,单个骨架颗粒的接触约束数量远大于12,因此对颗粒的变形限制也更加苛刻,骨架颗粒变形对孔隙度的影响程度进一步降低。
同时,数值实验中的球体接触面是微小的面接触,可以近似为点接触方式。这种接触方式带来的应力集中,也会放大接触位置的变形,从而放大孔隙度的减小量,而实际岩石的骨架颗粒由于存在胶结,接触方式均为面接触,孔隙度的变化量应更小。由此可见,岩石本体变形中,骨架颗粒的形状基本保持不变。开发过程中,油藏岩石依旧遵循孔隙度不变的原则。
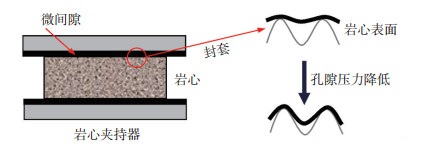
3.3 实验中孔隙度变化原因分析数值实验中的表皮为刚性表皮,约束壁面不发生位移和变形,仅仅发生了骨架颗粒的变形。数值实验表明,这种刚性表皮已经可以造成一定程度孔隙度的变化,然而,孔隙度测试实验中的表皮,是岩心夹持器封套和骨架颗粒组成的柔性表皮,约束面(封套)既可发生位移,又可以发生较大变形,而且变形能力和图 4(a)中模拟的变形比例一致(杨氏模量相同),具有较强的变形能力。实验过程中孔隙度变化幅度较大,这是封套与岩心界面上的接触表皮中的微间隙导致的。由于岩心表面不够光滑,接触表皮由岩心与封套之间的微间隙组成[23-25](图 12),当外应力增大或是内应力降低时,微间隙也会受到压缩,从而增大了岩石的孔隙度降低幅度。
|
下载原图 图 12 孔隙度测量过程中的微间隙 Fig. 12 Micro interstice during porosity measurement |
微间隙的变形源于夹持器封套变形,而封套材料的变形能力较强,其变形导致了岩心孔隙体积的大幅度降低。当采用压汞法或是其他方法测试孔隙度随应力变化时[26-28],孔隙度的下降幅度较小,这与本文得到的结果基本一致。
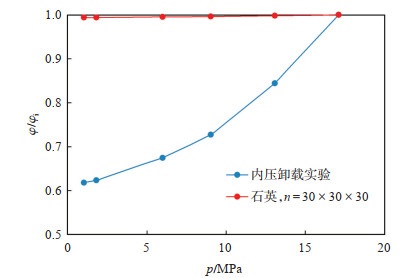
3.4 实例计算通过无因次孔隙度的计算,可以比较文献[10-12]中的孔隙度变化以及本文获得的孔隙度变化特征(图 13)。目前变外应力实验结果表明孔隙度的降低幅度大致为5%~40%[10-12],明显高于机理模型的计算值(10 MPa孔隙压力导致孔隙度减小0.12%)。
|
下载原图 图 13 无因次孔隙度变化比较 Fig. 13 Comparison of porosity change |
孔隙度的大幅度下降会给油藏充足的弹性能量,地层压力会因孔隙度的减小而升高,从而维持了地层能量和产能。以常规油藏为例,孔隙体积的变化量与孔隙压力的升高值之间存在下面的关系
| $ \Delta {{V}_{\text{p}}}={{V}_{\text{o}}}{{c}_{\text{o}}}\Delta p $ | (1) |
式中:Vp为孔隙体积变化量,m3;Vo为原油体积,m3;co为原油压缩系数,MPa-1;Δp为地层压力升高值,MPa。
若地层原油的压缩系数为10×10-4 MPa-1,油藏开采中,孔隙压力降低了10 MPa,则由式(1)可以计算出,若孔隙体积减小1%,地层压力则升高10 MPa,那么油藏压力不可能衰竭。
油气藏储量计算时,通常认为岩石的地面测量孔隙度和地下原地孔隙度是不相等的,因此在计算中把地面孔隙度测量值加载围压校正到地下状态,校正的相对值一般为地面孔隙度的5~10% 左右,即地下孔隙度比地面孔隙度低5~10%。根据本文的研究,这种校正没有必要,会低估油气储量。
4 结论(1)有约束条件的弹性变形中,骨架颗粒的形状发生变化,对多孔介质的孔隙度影响较小,且随着约束位置增加,骨架颗粒的变形特征越接近与无约束条件下的变形。
(2)油藏条件下,致密多孔介质(成岩后的岩石)孔隙度对应力的变化并不敏感,孔隙压力变化10 MPa可以导致10-3数量级的孔隙度变化,小于实验可测试的范围。
(3)岩心夹持器中的封套与岩心表面形成的微间隙导致了实验中较大的孔隙度变化,实验的误差源于柔性表皮对孔隙体积测试的影响。
(4)油藏孔隙压力下降导致的储层岩石压缩过程中,本体变形的各骨架颗粒形状不变的假设条件是合理的,开采油藏过程中,储层的孔隙度仍然遵循“本体变形过程中的孔隙度不变性原则”。
| [1] |
ISCAN A G, KOK M V, BAGC A S. Estimation of permeability and rock mechanical properties of limestone reservoir rocks under stress conditions by strain gauge. Journal of Petroleum Science and Engineering, 2006, 53(1/2): 13-24. |
| [2] |
薛丹, 张遂安, 吴新民, 等. 下寺湾油田长7油层组页岩气储层敏感性实验. 岩性油气藏, 2019, 31(3): 135-144. XUE D, ZHANG S A, WU X M, et al. Sensitivity experiment of shale gas reservoir of Chang 7 reservoir in Xiasiwan oilfield. Lithologic Reservoirs, 2019, 31(3): 135-144. |
| [3] |
毛小龙, 刘月田, 冯月丽, 等. 双重有效应力再认识及其综合作用. 石油科学通报, 2018, 3(4): 390-398. MAO X L, LIU Y T, FENG Y L, et al. Re-recognition of dual effective stresses and the comprehensive effect. Petroleum Science Bulletin, 2018, 3(4): 390-398. |
| [4] |
李传亮. 关于双重有效应力: 回应洪亮博士. 新疆石油地质, 2015, 36(2): 238-243. LI C L. Discussion on the dual effective stresses of porous media: Reply to Dr Hong Liang. Xinjiang Petroleum Geology, 2015, 36(2): 238-243. |
| [5] |
王继伟, 朱玉双, 饶欣久, 等. 鄂尔多斯盆地胡尖山地区长61致密砂岩储层成岩特征与孔隙度定量恢复. 岩性油气藏, 2020, 32(3): 34-43. WANG J W, ZHU Y S, RAO X J, et al. Diagenetic characteristics and quantitative porosity restoration of Chang 61 tight sandstone reservoir in Hujianshan area, Ordos Basin. Lithologic Reservoirs, 2020, 32(3): 34-43. |
| [6] |
郭艳琴, 何子琼, 郭彬程, 等. 苏里格气田东南部盒8段致密砂岩储层特征及评价. 岩性油气藏, 2019, 31(5): 1-11. GUO Y Q, HE Z Q, GUO B C, et al. Reservoir characteristics and evaluation of tight sandstone of He 8 member in southeastern Sulige Gas Field. Lithologic Reservoirs, 2019, 31(5): 1-11. |
| [7] |
邓浩阳, 司马立强, 吴玟, 等. 致密砂岩储层孔隙结构分形研究与渗透率计算: 以川西坳陷蓬莱镇组、沙溪庙组储层为例. 岩性油气藏, 2018, 30(6): 76-82. DENG H Y, SIMA L Q, WU W, et al. Fractal characteristics of pore structure and permeability calculation for tight sandstone reservoirs: a case of Penglaizhen Formation and Shaximiao Formation in western Sichuan Depression. Lithologic Reservoirs, 2018, 30(6): 76-82. |
| [8] |
王维斌, 朱静, 马文忠, 等. 鄂尔多斯盆地周家湾地区长8致密砂岩储层特征及影响因素. 岩性油气藏, 2017, 29(1): 51-58. WANG W B, ZHU J, MA W Z, et al. Characteristics and influencing factors of Chang 8 tight sandstone reservoir of Triassic Yanchang Formation in Zhoujiawan area, Ordos Basin. Lithologic Reservoirs, 2017, 29(1): 51-58. DOI:10.3969/j.issn.1673-8926.2017.01.007 |
| [9] |
王猛, 曾明, 陈鸿傲, 等. 储层致密化影响因素分析与有利成岩相带预测: 以马岭油田长8油层组砂岩储层为例. 岩性油气藏, 2017, 29(1): 59-70. WANG M, ZENG M, CHEN H A, et al. Influencing factors of tight reservoirs and favorable diagenetic facies: a case study of Chang 8 reservoir of the Upper Triassic Yanchang Formation in Maling Oilfield, Ordos Basin. Lithologic Reservoirs, 2017, 29(1): 59-70. |
| [10] |
丁景辰, 杨胜来, 胡伟, 等. 致密气藏应力敏感性实验. 大庆石油地质与开发, 2014, 33(3): 170-174. DING J C, YANG S L, HU W, et al. Indoor experiment in the stress sensitivity for tight gas reservoir. Petroleum Geology and Oilfield Development in Daqing, 2014, 33(3): 170-174. |
| [11] |
丁景辰, 杨胜来, 聂向荣, 等. 致密气藏的应力敏感性及其对气井单井产能的影响. 西安石油大学学报(自然科学版), 2014, 29(3): 63-67. DING J C, YANG S L, NIE X R, et al. Stress sensitivity of tight gas reservoir and its influence on productivity of gas well. Journal of Xi'an Shiyou University(Natural Science Edition), 2014, 29(3): 63-67. |
| [12] |
高树生, 熊伟. 有效应力对低渗低孔介质孔渗参数的影响. 辽宁工程技术大学学报(自然科学版), 2001, 20(4): 538-540. GAO S S, XIONG W. The effect of effective stress on the parameter of the low permeability. Journal of Liaoning Technical University(Natural Science), 2001, 20(4): 538-540. |
| [13] |
杨通佑, 范尚炯, 陈元千, 等. 石油及天然气储量计算方法. 北京: 石油工业出版社, 1990. YANG T Y, FAN S J, CHEN Y Q, et al. The computation method of oil and gas reserve. Beijing: Petroleum Industry press, 1990. |
| [14] |
李传亮, 孔祥言, 徐献芝, 等. 多孔介质的双重有效应力. 自然杂志, 1999, 21(5): 288-292. LI C L, KONG X Y, XU X Z, et al. Dual effective stress of porous media. Chinese Journal of Nature, 1999, 21(5): 288-292. |
| [15] |
李传亮, 朱苏阳. 关于应力敏感测试方法的认识误区. 岩性油气藏, 2015, 27(6): 1-4. LI C L, ZHU S Y. Misunderstanding of measuring methods of stress sensibility. Lithologic Reservoirs, 2015, 27(6): 1-4. |
| [16] |
李传亮. 有效应力概念的误用. 天然气工业, 2008, 28(10): 130-132. LI C L. Misusage of the concept of effective stress. Natural Gas Industry, 2008, 28(10): 130-132. |
| [17] |
李传亮. 储层岩石的压缩问题. 石油钻采工艺, 2010, 32(5): 120-124. LI C L. Discussion on the compression of reservoir rock. Oil Drilling & Production Technology, 2010, 32(5): 120-124. |
| [18] |
李传亮, 涂兴万. 储层岩石的2种应力敏感机制: 应力敏感有利于驱油. 岩性油气藏, 2008, 20(1): 111-113. LI C L, TU X W. Two types of stress sensitivity mechanisms for reservoir rocks: Being favorable for oil recovery. Lithologic Reservoirs, 2008, 20(1): 111-113. |
| [19] |
李传亮. 油藏工程原理. 北京: 石油工业出版社, 2011. LI C L. Fundamental of reservoir engineering. Beijing: Petroleum Industry Press, 2011. |
| [20] |
李传亮. 岩石本体变形过程中的孔隙度不变性原则: 同任勇和孙艾茵二位作者商榷. 新疆石油地质, 2005, 26(6): 130-132. LI C L. The principle of rock porosity invariability in primary deformation. Xinjiang Petroleum Geology, 2005, 26(6): 130-132. |
| [21] |
李传亮. 孔隙度校正缺乏理论依据. 新疆石油地质, 2003, 24(3): 254-256. LI C L. The porosity correction is lack of theoretical basis. Xinjiang Petroleum Geology, 2003, 24(3): 254-256. |
| [22] |
JAEGER J C, COOK N G W, ZIMMERMAN R W. Fundamentals of rock mechanics. 4th ed. Blackwell Publishing, 2007.
|
| [23] |
ZHU S Y. Experiment research of tight sandstone gas reservoir stress sensitivity based on the capillary bundle mode. SPE 167638, 2013.
|
| [24] |
李传亮. 岩石压缩系数测量新方法. 大庆石油地质与开发, 2008, 27(3): 53-54. LI C L. A new measurement method of rock compressibility. Petroleum Geology and Oilfield Development in Daqing, 2008, 27(3): 53-54. |
| [25] |
ZHU S Y, DU Z M, LI C L, et al. A semi-analytical model for pressure-dependent permeability of tight sandstone reservoirs. Transport in Porous Media, 2018, 122(2): 1-18. |
| [26] |
MBIA E N, FABRICIUS I L, KROGSBØLL A, et al. Permeability, compressibility and porosity of Jurassic shale from the Norwegian-Danish Basin. Petroleum Geoscience, 2014, 20(3): 257-281. |
| [27] |
WU H B, DONG S H, LI D H, et al. Experimental study on dynamic elastic parameters of coal samples. International Journal of Mining Science and Technology, 2015, 25(3): 447-452. |
| [28] |
GUO X, YAO Y, LIU D. Characteristics of coal matrix compressibility: an investigation by mercury intrusion porosimetry. Energy & Fuels, 2014, 28(6): 3673-3678. |
 2021, Vol. 33
2021, Vol. 33




