物质平衡法是油藏工程重要的研究方法,可以用来计算油气藏的地质储量、判断油气藏的驱动类型、估算油气藏天然水侵量、预测油气藏动态等。在应用物质平衡方程求解油藏实际问题时,一般都要对其进行线性化处理[1-4]。油藏累积采油量的地下体积与油藏压降之间的关系曲线被称为油藏生产指示曲线,封闭未饱和弹性驱动油藏的生产指示曲线被认为是一条直线,因此油藏生产指示曲线可以用来进行驱动类型的判断[3, 5]。把弹性驱动油藏的生产指示曲线看作一条直线的前提是油藏的有效压缩系数为常数,然而原油压缩系数并非常数,而是一个随着地层压力增大而减小的变量,只是在一定的压力范围之内,通常将其视为常数而已[3, 6]。因此,弹性驱动油藏的生产指示曲线并非一条直线,而是一条曲线,并且油藏压降越大,曲线偏离直线越明显。缝洞型碳酸盐岩油藏埋藏较深,如塔河油田奥陶系缝洞型油藏埋深5 300~7 000 m,地层压力较高,一般属于未饱和油藏,地层压力与饱和压力差值较大,可达50 MPa以上,原始地层压力与饱和压力下的原油压缩系数差别很大,可相差几倍,甚至十几倍[7-9]。因此,缝洞型油藏根据该油藏生产指示曲线进行油藏驱动类型判断、地质储量计算与油藏动态预测等研究将会存在明显的误差。
针对缝洞型碳酸盐岩油藏,通过建立原油体积系数、原油压缩系数与地层压力的函数关系式,简化弹性驱动物质平衡方程,建立新型的油藏生产指示曲线,以期能够更加准确地进行油藏研究。
1 油藏生产指示曲线存在问题弹性驱动是指开采原油的驱动能量全部来自油藏自身的弹性膨胀能,油藏为未饱和油藏,不存在气顶,油藏既不注水,也没有其他外来能量的参与。封闭未饱和孔隙型砂岩油藏弹性驱动的物质平衡方程可表示为[3]
| $ N_{\mathrm{p}} B_{\mathrm{o}}=N B_{\mathrm{oi}} C_{\mathrm{eff}} \Delta p $ | (1) |
| $ C_{\mathrm{eff}}=C_{\mathrm{o}}+\frac{S_{\mathrm{wi}} C_{\mathrm{w}}+C_{\mathrm{p}}}{S_{\mathrm{oi}}} $ | (2) |
式中:Np为地面条件下的累积产油量,万m3;N为地面条件下的原油地质储量,万m3;Bo为当前地层压力下原油的体积系数,m3/m3;Ceff为油藏的有效压缩系数,MPa-1;Boi为原始地层压力下原油的体积系数,m3/m3;Δp为油藏压降,MPa;Co,Cw,Cp分别为地层原油、地层水、岩石压缩系数,MPa-1;Swi为束缚水饱和度,小数;Soi为原始含油饱和度,小数。
缝洞型碳酸盐岩油藏的储集空间以大型溶洞为主,溶洞是主要的储集空间与产量的主要贡献者,灰岩基质不能作为有效储集层,而是以一种渗流屏障的形式存在[10-15]。为简化研究,忽略束缚水与岩石的压缩系数,仅考虑地层原油的压缩系数,因此缝洞型油藏的有效压缩系数可简化为
| $ {C_{{\rm{eff}}}} = {C_{\rm{o}}} $ | (3) |
由式(1)、式(2)、与式(3),得到封闭定容未饱和缝洞型油藏弹性驱动的物质平衡方程
| $ {N_{\rm{p}}}{B_{\rm{o}}} = N{B_{{\rm{oi}}}}{C_{\rm{o}}}\Delta p $ | (4) |
由式(4)可知,缝洞型油藏弹性驱动的油藏生产指示曲线,即累积采油量的地下体积NpBo与油藏压降Δp的关系曲线,其斜率为NBoiCo,由于油藏的原油地质储量N以及原始地层压力下的原油体积系数Boi为定值,因此油藏生产指示曲线的斜率取决于原油压缩系数Co的变化。
原油压缩系数是一个随着压力增大而减小的变量[3, 6, 8]。1980年,Vasquez等[16]在对4 036个实验数据点进行线性回归分析后,提出了饱和压力之上地层原油等温压缩系数的相关经验公式
| $ {C_{\rm{o}}} = \frac{{28.075{\kern 1pt} {R_{{\rm{sb}}}} + 30.96{\kern 1pt} T - 1{\kern 1pt} {\kern 1pt} 180{\kern 1pt} {\kern 1pt} {\gamma _{{\rm{gs}}}} + \frac{{1{\kern 1pt} {\kern 1pt} 784.315}}{{{\gamma _{\rm{o}}}}} - 2{\kern 1pt} {\kern 1pt} 540.815}}{{{{10}^5}{\kern 1pt} p}} $ | (5) |
| $ {\gamma _{{\rm{gs}}}} = {\gamma _{\rm{g}}}\left[ {1 + 0.248{\kern 1pt} {\kern 1pt} 8\left( {\frac{{1.076}}{{{\gamma _{\rm{o}}}}} - 1} \right)\left( {0.056{\kern 1pt} {\kern 1pt} 25{\kern 1pt} {T_{{\rm{sep}}}} + 1} \right)\left( {\log {p_{{\rm{sep}}}} + 0.101{\kern 1pt} {\kern 1pt} 9} \right)} \right] $ | (6) |
式中:Rsb为饱和压力下的溶解气油比,m3/m3;T为油藏温度,℃;p为地层压力,MPa;Tsep为分离器温度,℃;γgs为参考分离器压力0.689 MPa(100 psi)下分离气体的相对密度,小数;γo为油罐油相对密度,小数;γg为分离器压力与分离器温度下分离气体的相对密度,小数;psep为分离器压力,MPa。
| $ B = \frac{{28.075{\kern 1pt} {\kern 1pt} {R_{{\rm{sb}}}} + 30.96{\kern 1pt} {\kern 1pt} T - 1{\kern 1pt} {\kern 1pt} 180{\kern 1pt} {\kern 1pt} {\gamma _{{\rm{gs}}}} + \frac{{1{\kern 1pt} {\kern 1pt} 784.315}}{{{\gamma _{\rm{o}}}}} - 2{\kern 1pt} {\kern 1pt} 540.815}}{{{{10}^5}}} $ | (7) |
则原油压缩系数的Vasquez-Beggs经验公式,即式(6)可简化为
| $ {C_{\rm{o}}} = \frac{B}{p} $ | (8) |
由式(7)可知,当原油相对密度γo、天然气相对密度γg、油藏温度T与饱和压力下的溶解气油比Rsb一定时,系数B为常数,此时原油压缩系数Co只与地层压力p有关。由式(8)可知,地层原油的等温压缩系数Co与地层压力p成反比,地层压力p越大,原油压缩系数Co越小[8, 17-18]。
因此,缝洞型油藏弹性驱动的油藏生产指示曲线的斜率NBoiCo不是常数,而是随着地层压力增大而减小的变量,即弹性驱动的油藏生产指示曲线本身就是一条曲线,而非一条直线。如图 1所示,假设地层原油压缩系数为常数得到的油藏生产指示曲线直线形式,与实际的油藏生产指示曲线存在明显偏差,而且油藏压降越大,偏离直线越明显。因此,对于超深的缝洞型油藏来讲,利用该油藏生产指示曲线进行油藏驱动类型判断、地质储量计算以及水侵量的计算等将会产生很大的误差,需要进行改进。
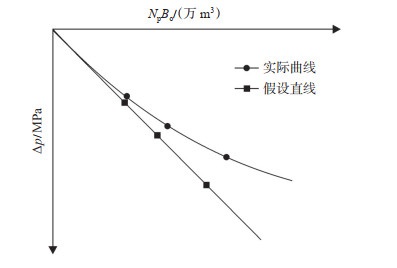
|
下载原图 图 1 封闭未饱和弹性驱动油藏的生产指示曲线 Fig. 1 Production index curve of closed unsaturated elastic drive reservoir |
油藏物质平衡方程中涉及的原油高压物性参数包括原油体积系数Bo与原油压缩系数Co,饱和压力之上两者均随着地层压力增大而减小。因此,通过建立原油体积系数、原油压缩系数与地层压力的函数关系式,简化物质平衡方程,从而建立新的油藏生产指示曲线。
地层原油的等温压缩系数是指单位压力变化下原油的体积变化率,可由原油体积系数表示[3]
| $ {C_{\rm{o}}} = - \frac{1}{{{B_{\rm{o}}}}}\frac{{{\rm{d}}{B_{\rm{o}}}}}{{{\rm{d}}p}} $ | (9) |
由式(9)可知,只要得到原油体积系数与地层压力的函数关系式,就可以得到原油压缩系数与地层压力的函数关系式。
2.1 原油体积系数与地层压力不符合线性关系目前一般是把饱和压力之上的原油体积系数与地层压力作为线性函数处理[19](图 2中的直线部分)。
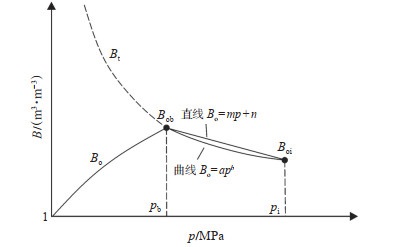
|
下载原图 图 2 原油体积系数与地层压力关系曲线 Fig. 2 Relationship curve that oil volume factor varies with formation pressure |
假设饱和压力之上原油体积系数与地层压力的线性函数关系式为
| $ {B_{\rm{o}}} = mp + n $ | (10) |
式中:m,n分别为函数关系式的斜率和截距,取常数。
由式(10)得到原油体积系数对地层压力的导数
| $ \frac{{{\rm{d}}{B_{\rm{o}}}}}{{{\rm{d}}p}} = m $ | (11) |
将式(11)代入式(9),得到饱和压力之上地层压力p对应的原油压缩系数Co为
| $ {C_{\rm{o}}} = - \frac{m}{{{B_{\rm{o}}}}} $ | (12) |
由式(12)可知,如果饱和压力之上的原油体积系数与地层压力为线性函数关系,那么原油压缩系数与原油体积系数成反比,即随着地层压力的增大,原油体积系数减小,而原油压缩系数增大,这与实际情况相矛盾。因此,饱和压力之上原油的体积系数与地层压力不符合线性关系。
2.2 原油体积系数与地层压力符合幂函数关系当地层压力高于饱和压力时,原油体积系数与地层压力的关系是非线性的[6, 8]。由于原油压缩系数与原油体积系数均随着地层压力的增大而减小,根据原油压缩系数的定义以及Vasquez-Beggs经验公式,假设饱和压力之上的原油体积系数与地层压力符合幂函数关系(图 2中的曲线部分),其关系式可表示为
| $ {B_{\rm{o}}} = a{p^b} $ | (13) |
式中:a,b分别为幂函数关系式的系数和指数,取常数。
利用原油高压物性资料中原始地层压力pi、饱和压力pb以及相对应的原油体积系数Boi与Bob,由式(13)联立方程求解得到系数a,b
| $ a=\frac{B_{\mathrm{oi}}}{p_{\mathrm{i}}{ }^{b}}=\frac{B_{\mathrm{ob}}}{p_{\mathrm{b}}{ }^{b}} $ | (14) |
| $ b=\frac{\ln \frac{B_{\mathrm{oi}}}{B_{\mathrm{ob}}}}{\ln \frac{p_{\mathrm{i}}}{p_{\mathrm{b}}}} $ | (15) |
式中:Bob为饱和压力之下原油的体积系数,m3/m3。
确定a,b的值后,就可以得到饱和压力之上任意地层压力p对应的原油体积系数Bo,Bo与饱和压力、原始地层压力下的原油体积系数Bob及Boi的关系式为
| $ B_{\mathrm{o}}=B_{\mathrm{ob}}\left(\frac{p}{p_{\mathrm{b}}}\right)^{b}=B_{\mathrm{oi}}\left(\frac{p}{p_{\mathrm{i}}}\right)^{b} $ | (16) |
由式(13)得到原油体积系数Bo对地层压力p的导数
| $ \frac{{{\rm{d}}{B_{\rm{o}}}}}{{{\rm{d}}p}} = ab{p^{b - 1}} $ | (17) |
将式(17)、式(13)代入式(9),得到饱和压力之上原油压缩系数Co与地层压力p的幂函数关系式为
| $ {C_{\rm{o}}} = - \frac{b}{p} $ | (18) |
对比式(18)与式(8)可以看出,假设饱和压力之上原油体积系数与地层压力满足幂函数关系得到的原油压缩系数与地层压力的幂函数关系式,与Vasquez-Beggs经验公式的形式完全一致。
因此,假设饱和压力之上的原油体积系数与地层压力满足幂函数关系是合理的。
2.3 原油压缩系数的使用从原油等温压缩系数的定义[式(9)]可以看出,原油压缩系数的使用存在2种情况:
一是饱和压力之上某一地层压力p对应的原油压缩系数,可记为Cop,表示为
| $ {C_{{\rm{op}}}} = - \frac{b}{p} $ | (19) |
二是饱和压力之上地层压力从p1下降到p2产生压降Δp,压力区间(p1,p2)所对应的平均原油压缩系数可记为CoΔp,如高压物性实验中测定不同压力区间的原油压缩系数[3, 20]。
对式(9)两边积分,得到压力区间(p1,p2)所对应的平均原油压缩系数CoΔp
| $ {C_{{\rm{o}}\Delta {\rm{p}}}} = - \frac{{\int_{{p_1}}^{{p_2}} {\frac{1}{{{B_0}}}} {\rm{d}}{B_{\rm{o}}}}}{{{p_2} - {p_1}}} = \frac{{\ln \frac{{{B_{{\rm{o}}2}}}}{{{B_{{\rm{ol}}}}}}}}{{\Delta p}} = \frac{{\ln {{\left( {\frac{{{p_2}}}{{{p_1}}}} \right)}^b}}}{{\Delta p}} $ | (20) |
对于一个具体的油藏来讲,投入开发后原始地层压力pi下降到某一地层压力p时,油藏压降Δp对应的平均原油压缩系数可记为CoΔpi,例如物质平衡方程式(4)中的原油压缩系数。
由式(20)可知,油藏压降Δp对应的平均原油压缩系数CoΔpi为
| $ {C_{{\rm{o}}\Delta {\rm{pi}}}} = \frac{{\ln \frac{{{B_{\rm{o}}}}}{{{B_{{\rm{oi}}}}}}}}{{\Delta p}} = \frac{{\ln {{\left( {\frac{p}{{{p_{\rm{i}}}}}} \right)}^b}}}{{\Delta p}} $ | (21) |
在油藏物质平衡方程中,不应使用地层压力p对应的原油压缩系数Cop,而应使用油藏压降Δp对应的平均原油压缩系数CoΔpi。
因此,封闭定容弹性驱动缝洞型油藏的物质平衡方程式应表示为
| $ {N_{\rm{p}}}{B_{\rm{o}}} = N{B_{{\rm{oi}}}}{C_{{\rm{o}}\Delta {\rm{pi}}}}\Delta p $ | (22) |
将油藏压降Δp对应的平均原油压缩系数CoΔpi [式(21)]代入式(22),缝洞型油藏弹性驱动的物质平衡方程式可变为
| $ {N_{\rm{p}}}{B_{\rm{o}}} = N{B_{{\rm{oi}}}}\ln \frac{{{B_{\rm{o}}}}}{{{B_{{\rm{oi}}}}}} = N{B_{{\rm{oi}}}}\ln {\left( {\frac{p}{{{p_{\rm{i}}}}}} \right)^b} $ | (23) |
式中:p/pi表示油藏地层压力保持水平;(p/pi)b为饱和压力之上地层压力p对应的原油体积系数Bo与原始地层压力pi对应的原油体积系数Boi的比值,表示油藏原油地质储量地下体积的弹性膨胀倍数;ln(p/pi)b表示油藏原油地质储量地下体积的弹性膨胀幅度。
由式(23)可知,油藏累积采油量的地下体积NpBo不是与油藏压降Δp成直线关系,而是与油藏弹性膨胀幅度ln(p/pi)b成直线关系。
将饱和压力之上地层压力p对应的原油体积系数Bo[式(13)]代入式(23),就可以得到形式更加简单的缝洞型油藏弹性驱动的物质平衡方程式
| $ {N_{\rm{p}}} = N\frac{{\ln {{\left( {\frac{p}{{{p_{\rm{i}}}}}} \right)}^b}}}{{{{\left( {\frac{p}{{{p_{\rm{i}}}}}} \right)}^b}}} $ | (24) |
利用生产数据来绘制出累积产油量Np与ln(p/pi)b/(p/pi)b的关系曲线,即可得到缝洞型油藏弹性驱动的新型油藏生产指示曲线(图 3)。
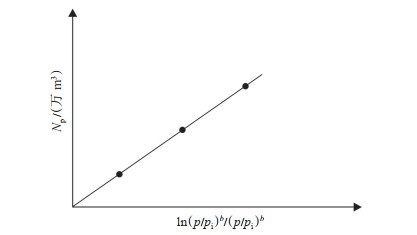
|
下载原图 图 3 缝洞型油藏弹性驱动的新型油藏生产指示曲线 Fig. 3 New production index curve of elastic drive reservoir for fractured-vuggy carbonate reservoirs |
如图 3所示,缝洞型油藏弹性驱动的新型油藏生产指数曲线始终为一条直线,且直线的斜率即为油藏的原油地质储量N。
弹性驱动的新型油藏生产指数曲线的横坐标ln(p/pi)b/(p/pi)b即为油藏弹性驱动的采出程度
| $ {R_{\rm{o}}} = \frac{{{N_{\rm{p}}}}}{N} = \frac{{\ln {{\left( {\frac{p}{{{p_{\rm{i}}}}}} \right)}^b}}}{{{{\left( {\frac{p}{{{p_{\rm{i}}}}}} \right)}^b}}} $ | (25) |
若油藏发生水侵,物质平衡方程可表示为
| $ N_{\mathrm{p}} B_{\mathrm{o}}+W_{\mathrm{p}} B_{\mathrm{w}}=N B_{\mathrm{oi}} C_{\mathrm{o} \Delta \mathrm{pi}} \Delta p+W_{\mathrm{e}} $ | (26) |
式中:Wp为地面条件下的累积产水量,m3;We为油藏水侵量的地下体积,m3;Bw为当前地层压力下地层水的体积系数,m3/m3。
将式(13)与式(21)代入式(26),得到
| $ N_{\mathrm{p}}=N \frac{\ln \left(\frac{p}{p_{\mathrm{i}}}\right)^{b}}{\left(\frac{p}{p_{\mathrm{i}}}\right)^{b}}+\frac{W_{\mathrm{e}}-W_{\mathrm{p}} B_{\mathrm{w}}}{B_{\mathrm{o}}} $ | (27) |
从式(27)可以看出,若油藏发生明显水侵,新型油藏生产指示曲线将偏离直线。因此,新型油藏生产指示曲线可以更加准确地判断驱动类型。
4 实例计算某缝洞型油藏A油井,生产井段为6 458~ 6 550 m,油藏温度T为141.7 ℃,原始地层压力pi为72.27 MPa,饱和压力pb为24.19 MPa,原油体积系数Boi,Bob分别为1.508 3 m3/m3,1.678 5 m3/m3,饱和压力下的溶解气油比Rsb为177 m3/m3,分离器温度Tsep为34.9 ℃,分离器压力psep为1.04 MPa,油罐油相对密度γo = 0.817 9,分离气相对密度γg = 0.684 0,参考分离器压力下分离气体的相对密度γgs= 0.705 0。
4.1 原油体积系数计算结果利用式(14)、式(15)计算得到A井原油体积系数Bo与地层压力p的幂函数关系式的斜率a = 2.291 3,截距b = -0.098。因此,A井饱和压力之上原油体积系数Bo与地层压力p的幂函数关系式为
| $ {B_{\rm{o}}} = 2.291{\kern 1pt} {\kern 1pt} 3{p^{ - 0.098}} $ | (28) |
如表 1所列,原油体积系数幂函数关系式的计算值与实验值的平均相对误差仅为0.02%,计算精度远大于线性函数关系式的计算值(平均相对误差2%)。
|
|
下载CSV 表 1 A井饱和压力之上原油体积系数Bo计算结果对比 Table 1 Comparison of calculation results of oil volume factor Bo above oil saturation pressure of well A |
如图 4所示,线性函数关系式明显不符合原油体积系数的变化规律,而原油体积系数与地层压力幂函数关系式的计算值与实验值几乎重合,不仅符合实际变化规律,而且计算精度高。
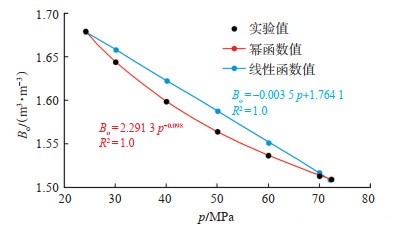
|
下载原图 图 4 A井饱和压力之上原油体积系数Bo计算结果对比 Fig. 4 Comparison of calculation results of oil volume factor Bo above oil saturation pressure of well A |
在得到了A井的原油体积系数Bo与地层压力p的幂函数关系式后,利用式(18)就可以得到饱和压力之上原油压缩系数Cop与地层压力p的幂函数关系式
| $ {C_{{\rm{op}}}} = \frac{{0.098}}{p} $ | (29) |
由A井的相关参数可以计算得到原油压缩系数Vasquez-Beggs经验公式中的系数B = 0.082,因此A井饱和压力之上地层压力p对应的原油压缩系数的Vasquez-Beggs经验公式为
| $ {C_{{\rm{op}}}} = \frac{{0.082}}{p} $ | (30) |
计算结果表明:假设饱和压力之上原油体积系数与地层压力为线性关系,得到的原油压缩系数随着地层压力的增大而增大,不符合实际变化规律,而假设原油体积系数与地层压力为幂函数关系,则与Vasquez-Beggs经验公式变化趋势一致,符合实际变化规律,原油压缩系数均随着地层压力的增大而减小,只是两者之间存在一定的误差,如图 5所示。
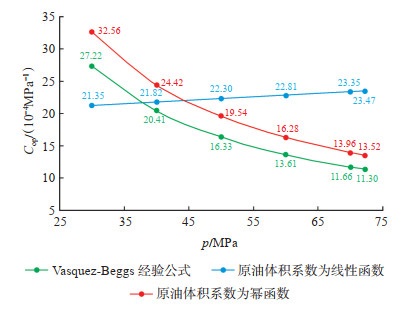
|
下载原图 图 5 A井饱和压力之上地层压力p对应的原油压缩系数Cop的计算结果对比 Fig. 5 Comparison of calculation results of oil compressibility Cop at a certain formation pressure p above oil saturation pressure of well A |
原油高压物性实验中测定原油压缩系数一般分多个压力区间分别进行测试。由式(20)得到A井饱和压力之上不同压力区间的平均原油压缩系数CoΔp为
| $ {C_{{\rm{o}}\Delta {\rm{p}}}} = \frac{{ - 0.098}}{{\Delta p}}\ln \frac{{{p_2}}}{{{p_1}}} $ | (23) |
如表 2所列,不同压力区间的平均原油压缩系数值与实验值的相对误差约为2.8%,而VasquezBeggs经验公式的计算值与实验值的相对误差约为18.5%,前者精度更高。
|
|
下载CSV 表 2 A井饱和压力之上不同压力区间的平均原油压缩系数Co∆p计算结果对比 Table 2 Comparison of calculation results of average oil compressibility Co∆p in different pressure ranges above oil saturation pressure of well A |
如图 6所示,饱和压力之上原油体积系数、原油压缩系数与地层压力的幂函数关系式不仅符合实际变化规律,而且具有较高的计算精度。
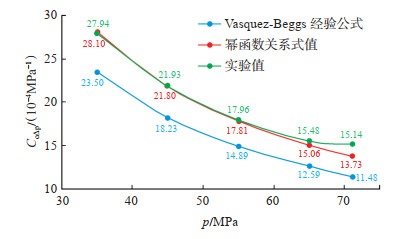
|
下载原图 图 6 A井饱和压之上不同压力区间的平均原油压缩系数Co∆p计算结果对比 Fig. 6 Comparison of calculation results of average oil compressibility Co∆p in different pressure ranges above oil saturation pressure of well A |
如图 7(b)所示,A井弹性驱动中NpBo与ln(p/pi)b始终保持直线关系,直线的斜率NBoi为19.882,再除以原始地层压力pi对应的原油体积系数Boi(1.508 3 m3/m3),就可以得到A井的原油地质储量N为13.182万m3。
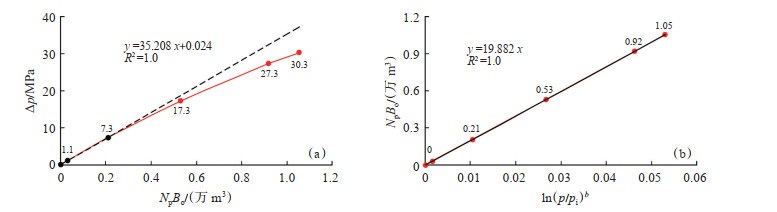
|
下载原图 图 7 A井弹性驱动NpBo与∆p(a),ln(p/pi)b(b)的关系曲线 Fig. 7 Relationships of elastic drive NpBo with ∆p (a) and ln(p/pi)b (b) of well A |
A井弹性驱动的新型油藏生产指示曲线始终为一条直线(图 8),直线的斜率即为原油地质储量N(13.182万m3)。因此,新型油藏生产指示曲线不存在原油藏生产指示曲线由于拟合直线数据点选取的不同造成原油地质储量计算结果存在多解性的问题。
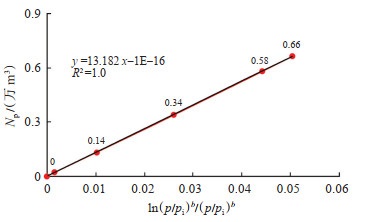
|
下载原图 图 8 A井弹性驱动新型油藏生产指示曲线 Fig. 8 New production index curve of elastic drive reservoir of well A |
A井生产数据表明:累积采油量的地下体积NpBo与油藏压降Δp不是线性关系而是曲线关系[图 7(a)],与油藏弹性膨胀幅度ln(p/pi)b成线性关系[图 7(b)]。
如图 7(a)所示,A井原油藏生产指示曲线为一条曲线,随着油藏压降的增大,地层压力越来越小,原油压缩系数越来越大,导致原油藏生产指示曲线偏离直线越来越明显。因此,原油藏生产指示曲线拟合直线数据点选取的不同将会使得原油地质储量的计算结果存在多解性。图 7(a)中3个数据点的拟合直线计算得到的地质储量为12.438万m3,而2个数据点与4个数据点的拟合直线计算得到的地质储量分别为11.862万m3、13.480万m3。
5 结论(1)封闭未饱和弹性驱动油藏的生产指示曲线被认为是一条直线,但由于原油的压缩系数是一个随着地层压力增大而减小的变量,因此弹性驱动油藏的生产指示曲线并非一条直线,而是一条曲线,并且油藏压降越大,曲线偏离直线越明显。
(2)饱和压力之上原油体积系数与地层压力不符合线性关系,而是符合幂函数关系。在油藏物质平衡分析中,应使用原始地层压力下降到某一地层压力产生的油藏压降所对应的平均原油压缩系数。
(3)对于封闭定容未饱和弹性驱动缝洞型油藏,通过建立原油体积系数、原油压缩系数与地层压力的函数关系式,简化物质平衡方程,建立的新型油藏生产指示曲线为一条直线,其斜率为原油地质储量。
(4)饱和压力之上原油体积系数、原油压缩系数与地层压力的幂函数关系式不仅符合实际变化规律,而且具有很高的计算精度。在此基础上建立的新型油藏生产指示曲线可以更加准确地进行油藏驱动类型判断、储量计算等油藏研究。
| [1] |
陈元千, 李璗. 现代油藏工程. 北京: 石油工业出版社, 2001: 88-111. CHEN Y Q, LI D. Modern petroleum reservoir engineering. Beijing: Petroleum Industry Press, 2001: 88-111. |
| [2] |
姜汉桥, 姚军, 姜瑞忠. 油藏工程原理与方法. 东营: 中国石油大学出版社, 2006: 200-234. JIANG H Q, YAO J, JIANG R Z. Reservoir engineering principles and methods. Dongying: China University of Petroleum Press, 2006: 200-234. |
| [3] |
李传亮. 油藏工程原理. 北京: 石油工业出版社, 2011: 144-185. LI C L. Fundamentals of reservoir engineering. Beijing: Petroleum Industry Press, 2011: 144-185. |
| [4] |
AHMED T. Reservoir engineering handbook(5th Edition). Oxford: Gulf Professional Publishing, 2018, 767-791. |
| [5] |
李传亮. 油藏生产指示曲线. 新疆石油地质, 2001, 22(4): 333-334. LI C L. Production index curves of reservoirs. Xinjiang Petroleum Geology, 2001, 22(4): 333-334. DOI:10.3969/j.issn.1001-3873.2001.04.020 |
| [6] |
何更生, 唐海. 油层物理. 北京: 石油工业出版社, 2011: 169-170. HE G S, TANG H. Petrophysics. Beijing: Petroleum Industry Press, 2011: 169-170. |
| [7] |
窦之林. 塔河油田碳酸盐岩缝洞型油藏开发技术. 北京: 石油工业出版社, 2012: 1-2. DOU Z L. The development technology of carbonate fracturedcavity reservoirs in Tahe oilfield. Beijing: Petroleum Industry Press, 2012: 1-2. |
| [8] |
凌建军, 黄鹂, 王尤富. 计算超深油藏地层原油体积系数的精确公式. 新疆石油地质, 1997, 18(4): 377-379. LING J J, HUANG L, WANG Y F. An accuracy formula for calculating formation oil volume factor for ultradeep reservoir. Xinjiang Petroleum Geology, 1997, 18(4): 377-379. |
| [9] |
李阳, 康志江, 薛兆杰, 等. 中国碳酸盐岩油气藏开发理论与实践. 石油勘探与开发, 2018, 45(4): 669-678. LI Y, KANG Z J, XUE Z J, et al. Theories and practices of carbonate reservoirs development in China. Petroleum Exploration and Development, 2018, 45(4): 669-678. |
| [10] |
程飞. 缝洞型碳酸盐岩油藏储层类型动静态识别方法: 以塔里木盆地奥陶系为例. 岩性油气藏, 2017, 29(3): 76-82. CHENG F. Integrated dynamic and static identification method of fractured-vuggy carbonate reservoirs: a case from the Ordovician in Tarim Basin. Lithologic Reservoirs, 2017, 29(3): 76-82. |
| [11] |
李阳, 侯加根, 李永强. 碳酸盐岩缝洞型储集体特征及分类分级地质建模. 石油勘探与开发, 2016, 43(4): 600-606. LI Y, HOU J G, LI Y Q. Features and hierarchical modeling of carbonate fracture-cavity reservoirs. Petroleum Exploration and Development, 2016, 43(4): 600-606. |
| [12] |
杨鹏飞, 张丽娟, 郑多明, 等. 塔里木盆地奥陶系碳酸盐岩大型缝洞集合体定量描述. 岩性油气藏, 2013, 25(6): 89-94. YANG P F, ZHANG L J, ZHENG D M, et al. Quantitative characterization of Ordovician carbonate fracture-cavity aggregate in Tarim Basin. Lithologic Reservoirs, 2013, 25(6): 89-94. DOI:10.3969/j.issn.1673-8926.2013.06.016 |
| [13] |
LIGAARDEN I S, KROTKIEWSKI M, KNUT-ANDREAS L, et al. On the Stokes-Brinkman equations for modeling flow in carbonate reservoirs. Ecmor Xii-european Conference on the Mathematics of Oil Recovery, Oxford, 2010.
|
| [14] |
刘鹏飞, 姜汉桥, 徐晖, 等. 缝洞型油藏开发室内模拟研究. 石油钻采工艺, 2009, 31(5): 72-76. LIU P F, JIANG H Q, XU H, et al. Laboratory simulation study on exploitation of fractured and cavernous reservoirs. Oil Drilling & Production Technology, 2009, 31(5): 72-76. |
| [15] |
王蓓, 刘向君, 司马立强, 等. 磨溪龙王庙组碳酸盐岩储层多尺度离散裂缝建模技术及其应用. 岩性油气藏, 2019, 31(2): 124-133. WANG B, LIU X J, SIMA L Q, et al. Multi-scale discrete fracture modeling technology for carbonate reservoir of Longwangmiao Formation in Moxi area and its application. Lithologic Reservoirs, 2019, 31(2): 124-133. |
| [16] |
VAZQUEZ M E, BEGGS H D. Correlations for fluid physical property prediction. Journal of Petroleum Technology, 1980, 32(6): 968-970. DOI:10.2118/6719-PA |
| [17] |
周庆军, 张甲清, 马华丽. 原油高压物性参数计算方法及对比. 油气井测试, 2003, 12(2): 31-34. ZHOU Q J, ZHANG J Q, MA H L. Algorithm and its contrast aimed at oil PVT parameters. Well Testing, 2003, 12(2): 31-34. |
| [18] |
谢龙, 郭绪强, 陈光进, 等. 计算原油体积系数的状态方程法. 中国石油大学学报(自然科学版), 2007, 31(3): 137-147. XIE L, GUO X Q, CHEN G J, et al. A new method predicting volume factor of formation crude oil. Journal of China University of Petroleum(Edition of Natural Science), 2007, 31(3): 137-147. |
| [19] |
蔡勇胜, 信德发, 陈国强. 封闭型弹性驱动油藏地层压力预测方法探讨. 内蒙古石油化工, 2010, 36(22): 56-57. CAI Y S, XIN D F, CHEN G Q. Discussion on prediction methods of formation pressure for closed elastic drive reservoirs. Inner Mongolia Petrochemical Industry, 2010, 36(22): 56-57. |
| [20] |
DANESH, ALI. PVT and phase behaviour of petroleum reservoir fluids. Developments in Petroleum Science, 1998, 11(1): 1-3. |
 2021, Vol. 33
2021, Vol. 33




