2. 中国石化华东油气分公司 临汾煤层气分公司, 山西 临汾 041000
2. Linfen Coalbed Methane Company, Sinopec East China Oil & Gas Company, Linfen 041000, Shanxi, China
我国致密油资源十分丰富,有着极其广阔的勘探开发前景[1-2]。但由于致密储层低孔、低渗、储层非均质性强等特点,使得致密油藏开发难度大,采收率低[3-4]。自发渗吸是亲水性致密储藏中一种重要的开发机理,充分发挥自发渗吸驱油作用对提高致密油藏采收率具有重要意义[5]。学者们开展大量的室内实验并构建了相应的数学模型[6-9],研究发现影响渗吸的因素主要包括岩心物性参数[10-12]、流体性质[13-14]及外界条件[15-16]。
由于致密储层中存在大量微纳米孔隙,使得致密储层孔隙结构极其复杂,储层内部流体流动困难,但微纳米孔隙的存在也使得致密储层中毛管力增大,渗吸驱动力增强[17]。因而确定岩心内部孔隙大小及分布对致密砂岩渗吸研究有着重要意义[18]。近年来,高压压汞、核磁共振[19-20]、CT扫描等技术被用于获取岩心孔隙结构,并与室内岩心渗吸实验相结合研究岩心渗吸过程。2016年韦青等[21]结合核磁共振技术对鄂尔多斯盆地吴起地区长8储层致密砂岩进行渗吸实验研究,结果表明孔隙结构好且孔喉连通程度高的亲水性致密砂岩储层渗吸作用明显。2019年顾雅頔等[22]利用铸体薄片等技术对致密岩心自发渗吸特征及影响因素进行研究,发现中大孔型的岩心自发渗吸驱油效果好于微小孔型岩心。2019年,杨柳等[23]利用渗吸指数与扩散指数将致密储层渗吸特征与孔径分布相结合研究发现,渗吸指数越大,宏孔越发育。扩散指数越大,中孔越发育。
致密储层孔喉结构十分复杂,其对致密油藏的渗吸有着极大的影响。国内外学者对致密砂岩孔喉结构及渗吸影响规律进行了大量的实验研究,但对致密砂岩孔喉结构对渗吸影响规律研究较少。本次研究利用合适函数对致密砂岩孔喉分布准确拟合,并利用渗吸模型预测致密砂岩渗吸驱油速率及渗吸采出程度,明确致密砂岩孔喉分布对致密砂岩渗吸影响规律,以期为致密油藏开采制度的确定提供一定的理论依据。
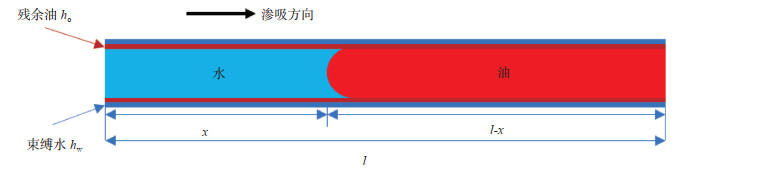
1 自发渗吸驱油数学模型假设致密砂岩基质孔隙由大量毛管束组成,在渗吸过程中,忽略重力影响,在毛管力的作用下,水自发驱替原油。假设毛管的长度为l,半径为r,t时刻油水界面的位移距离为x,束缚水与残余油分别以水膜、油膜形式存在,厚度分别为hw、ho(图 1),不同毛管半径中水膜、油膜厚度占比相同,则毛管渗流有效半径计算公式为[24]
| $ {r_{\rm{e}}} = r - {h_{\rm{o}}} - {h_{\rm{w}}} = r\sqrt {1 - {S_{{\rm{or}}}} - {S_{{\rm{wi}}}}} $ | (1) |
|
下载原图 图 1 含边界层毛细管自发渗吸驱油示意图[24] Fig. 1 Schematic diagram of oil displacement by spontaneous imbibition in a single capillary with boundary layers |
式中:re为有效半径,m;hw为水膜厚度,m;ho为油膜厚度,m;Sor为残余油饱和度;Swi为束缚水饱和度。
根据泊肃叶定律,在t时刻,毛管中油水两相渗流速度[25]可以表示为
| $ v_{w}=\frac{\mathrm{d} x}{\mathrm{~d} t}=\frac{r_{\mathrm{e}}^{2} p_{\mathrm{c}}}{8 \mu_{\mathrm{w}} x} $ | (2) |
| $ v_{\mathrm{o}}=\frac{\mathrm{d} x}{\mathrm{~d} t}=\frac{r_{\mathrm{e}}^{2} p_{\mathrm{c}}}{8 \mu_{\mathrm{o}}(l-x)} $ | (3) |
式中:vw为水相流速,m/s;vo为油相流速,m/s;μw为水相黏度,Pa·s;μo为油相黏度,Pa·s;pc为毛管力,Pa;l为毛管长度,m;x为油水界面位移距离,m。
由于液体是连续流动,且两相界面处速度相等,即vw = vo,由式(2)和式(3)可得
| $ \frac{\mathrm{d} x}{\mathrm{~d} t}=\frac{r_{\mathrm{e}}^{2} p_{\mathrm{c}}}{8\left[\mu_{\mathrm{w}} x+\mu_{\mathrm{o}}(l-x)\right]} $ | (4) |
分离变量并积分可得油水界面位移公式为
| $ x = \frac{{{\mu _{\rm{o}}}l - \sqrt {{{\left( {{\mu _{\rm{o}}}l} \right)}^2} - \left( {{\mu _{\rm{o}}} - {\mu _{\rm{w}}}} \right)\frac{{\sigma \ {r_{\rm{e}}}\cos \theta }}{2}t} }}{{{\mu _{\rm{o}}} - {\mu _{\rm{w}}}}} $ | (5) |
式中:σ为界面张力,N/m;θ为润湿角,(°)。
由
| $ v = \frac{{{\rm{d}}x}}{{{\rm{d}}t}} = \frac{{\sigma \ r\cos \theta }}{{4\sqrt {{{\left( {{\mu _{\rm{o}}}l} \right)}^2} - \left( {{\mu _{\rm{o}}} - {\mu _{\rm{w}}}} \right)\frac{{\sigma \ {r_{\rm{e}}}\cos \theta }}{2}t} }} $ | (6) |
当岩心存在迂曲度τ,毛细管实际长度为L = τl,则单根毛管t时刻流量为
| $ q(t) = v{\rm{ \mathsf{ π} }}r_e^2 = \frac{{{\rm{ \mathsf{ π} }}\sigma r_{\rm{e}}^3\cos \theta }}{{4\sqrt {{{\left( {{\mu _{\rm{o}}}L} \right)}^2} - \left( {{\mu _{\rm{o}}} - {\mu _{\rm{w}}}} \right)\frac{{\sigma {r_{\rm{e}}}\cos \theta }}{2}t} }} $ | (7) |
式中:q(t)为t时刻流量,m3/s,L为毛管实际长度,m。
由于岩心孔喉分布频率dSHg/d(lg r)与岩心半径lg r满足函数f(r),则半径介于r至r + d r的毛管数目为
| $ {\rm{d}}N(r) = \frac{{{V_{\rm{p}}}f(\lg r)}}{{{\rm{ \mathsf{ π} }}{r^2}L}}{\rm{d}}(\lg r) = \frac{{\varphi {d^2}}}{{4\ln 10\tau {r^3}}}f(\lg r){\rm{d}}r $ | (8) |
式中:Vp为孔隙体积,m3;d为岩心直径,m。
式(8)从rmin至rmax进行积分可得t时刻渗吸驱油总流量为
| $ \begin{array}{l} Q(t) = \int_{{r_{\min }}}^{{r_{\max }}} q \left( {{r_{\rm{e}}}} \right){\rm{d}}N(r) = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_{{r_{\min }}}^{{r_{\max }}} q \left( {{r_{\rm{e}}}} \right)\frac{{\varphi {d^2}}}{{4\ln 10\tau {r^3}}}f(\lg r){\rm{d}}r \end{array} $ | (9) |
式(9)进行积分可得t时刻岩心渗吸采出油体积为
| $ V(t) = \int_0^t {\int_{{r_{{\rm{min}}}}}^{{r_{\max }}} q } \left( {{r_{\rm{e}}}} \right)\frac{{\varphi {d^2}}}{{4\ln 10\tau {r^3}}}f(\lg r){\rm{d}}r{\rm{d}}t $ | (10) |
t时刻岩心渗吸采出程度为
| $ R(t) = \frac{{V(t)}}{{{V_{\rm{p}}}\left( {1 - {S_{{\rm{wi}}}}} \right)}} $ | (11) |
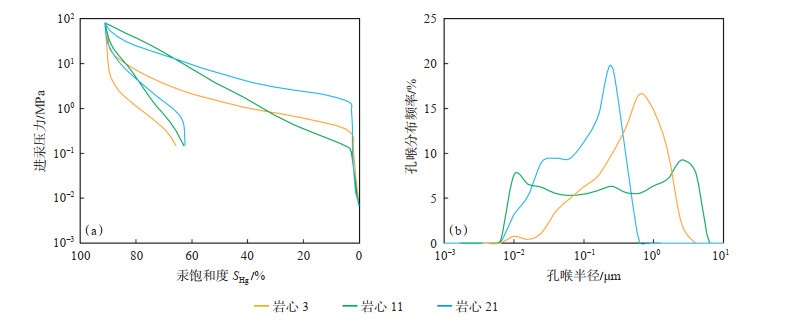
高压压汞法是测量岩心孔隙结构最常见的方法。Wang等[26]利用高压压汞测试对鄂尔多斯盆地延长组致密砂岩孔隙分布及分形特征进行研究,选取了其中3块致密砂岩进行渗吸模拟实验,其岩心毛管力曲线、孔喉分布频率如图 2所示,高压压汞部分岩心参数如表 1所列。岩心11气测渗透率最高,为2.290 mD,孔喉分布范围广泛,岩心最大孔喉半径、平均孔喉半径及孔喉半径中值均偏大;岩心21渗透率最小,为0.104 mD,孔喉半径集中分布于0.1 μm左右,且岩心分选系数最小;岩心3渗透率介于两者之间,孔喉半径集中分布在1.0 μm左右,且大孔喉所占比例较大。结果表明:随岩心渗透率增加,最大孔喉半径增大,孔喉分布曲线向右移动。
|
下载原图 图 2 3块致密砂岩岩心毛管力曲线及孔喉分布[26] Fig. 2 Capillary pressure curves and pore throat size distribution of three tight sandstone core samples |
|
|
下载CSV 表 1 3块致密砂岩孔喉参数 Table 1 Pore throat parameters of three tight sandstone core samples |
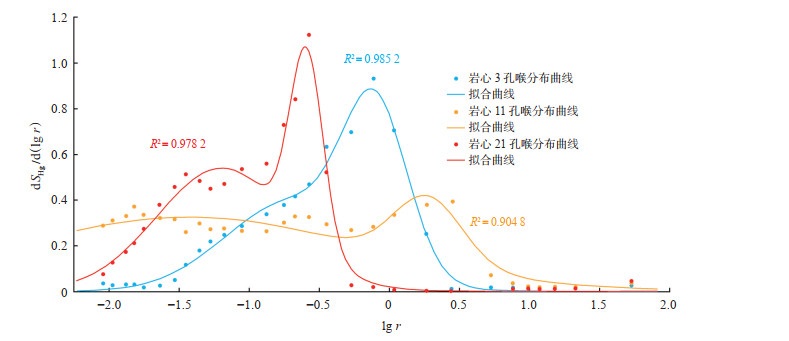
对岩心孔喉分布与岩心半径对数进行拟合,发现岩心孔喉分布频率dSHg/d(lg r)与孔喉半径对数lg r在半对数图上呈二维高斯分布(图 3)。二维高斯分布函数可表示为
| $ f(x) = {\text{a}_1}{\kern 1pt} {{\rm{e}}^{ - \left[ {{{\left( {\frac{{x - {\text{b}_1}}}{{{\text{c}_1}}}} \right)}^2}} \right]}} + {\text{a}_2}{\kern 1pt} {{\rm{e}}^{ - \left[ {{{\left( {\frac{{x - {\text{b}_1}}}{{{\text{c}_2}}}} \right)}^2}} \right]}} $ | (12) |
|
下载原图 图 3 基于二阶高斯分布的致密岩心孔喉分布曲线拟合 Fig. 3 Fitting of pore throat distribution curves based on second-order Gaussian distribution |
式中:a1,b1,c1,a2,b2,c2均为常数项。
为验证利用二维高斯分布函数拟合孔喉分布的准确性,基于毛管束模型,利用拟合函数对岩心渗透率进行计算。
根据泊肃叶定律可得单根毛管流量为
| $ q = \frac{{{\rm{ \mathsf{ π} }}{\kern 1pt} {r^4}\Delta p}}{{8\mu {\kern 1pt} L}} $ | (13) |
联立式(7)、式(8)与式(13),并对其从最小孔喉半径至最大孔喉半径进行积分可得总流量为
| $ Q = \int_{{r_{{\rm{min }}}}}^{{r_{\max }}} q {\rm{d}}N = \frac{{{\rm{ \mathsf{ π} }}{\kern 1pt} \Delta {\kern 1pt} p{\kern 1pt} \varphi {\kern 1pt} {d^2}}}{{32\ln 10\tau {\kern 1pt} \mu {\kern 1pt} L}}\int_{{r_{{\rm{min }}}}}^{{r_{\max }}} r f(\lg r){\rm{d}}{\kern 1pt} r $ | (14) |
根据达西公式可得岩心渗透率表达式为
| $ K = \frac{\varphi }{{8\ln 10{\tau ^2}}}\int_{{r_{\min }}}^{{r_{\max }}} r f(\lg r){\rm{d}}{\kern 1pt} r $ | (15) |
将拟合得到的孔喉频率分布函数、迂曲度等参数代入式(15)可计算岩心渗透率。根据上述3块致密砂岩岩心参数,计算出各岩心渗透率(表 2)。模型计算得到的渗透率与岩心实验气测渗透率均处于同一数量级,表明利用二维高斯分布拟合得到的致密砂岩孔喉分布有着较强的适用性。岩心11模型计算渗透率值比实验气测渗透率值偏大,其原因为岩心渗透率主要取决于大孔的分布,而大孔孔喉分布的拟合函数比实际孔喉分布偏大(图 3)。因此,可以通过进一步调整大孔孔喉分布拟合精度来降低模型计算误差。
|
|
下载CSV 表 2 3块岩心模型计算渗透率与实测渗透率对比 Table 2 Comparison of calculated permeability with measured permeability of three core samples |
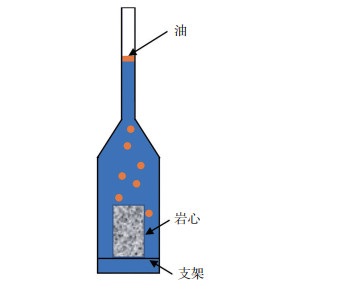
为验证构建的渗吸数学模型的准确性,选取鄂尔多斯盆地延长组1块典型致密砂岩岩心(表 3),对其开展室内渗吸实验(图 4)。实验步骤:①在105 ℃下对岩心进行烘干,待岩心重量不再变化时,对岩心进行抽真空,随后加压25 MPa进行岩心饱和。②饱和完成后,除去岩心表面的浮油,然后将岩心竖直放入渗吸瓶中;加入渗吸液淹没岩心并且进入渗吸瓶上部刻度管中适当位置,将渗吸瓶密封好,放入35 ℃恒温箱中开始渗吸。③溶液接触岩心底部的时间作为渗吸时间的起点,记录不同时刻岩心的渗吸情况。
|
|
下载CSV 表 3 实验岩心及流体参数 Table 3 Parameters of core samples and fluids |
|
下载原图 图 4 渗吸实验示意图 Fig. 4 Schematic diagram of spontaneous imbibition experiment |
同时,从鄂尔多斯盆地延长组选取1块同实验岩心孔隙度、渗透率等物性相近(岩心孔隙度为13.51%,渗透率为0.189 mD)的致密砂岩岩心进行高压压汞测试,利用二维高斯分布对孔喉分布进行拟合,并将拟合得到的孔喉分布函数代入渗吸模型,分别计算不同时刻岩心的渗吸采出程度及渗吸驱油速率。高压压汞得到孔喉分布及二维高斯分布拟合函数如图 5所示。
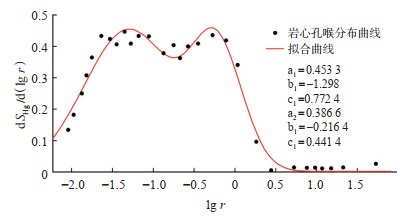
|
下载原图 图 5 高压压汞得到的致密岩心孔喉分布与二维高斯函数拟合结果 Fig. 5 Pore throat size distribution obtained by highpressure mercury intrusion and the fitted results by two-dimensional Gaussian function |
渗吸实验测得的渗吸采出程度与数学模型模拟得到的渗吸采出程度随时间变化曲线见图 6。二者能够很好地拟合,有着较强的相关性。这表明基于岩心孔喉分布所构建的渗吸模型能够用于致密砂岩渗吸驱油模拟。
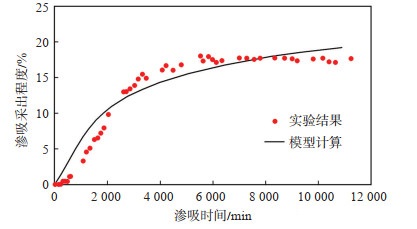
|
下载原图 图 6 模型计算得到的渗吸采出程度与实验测得渗吸采出程度对比 Fig. 6 Comparison of oil recovery degree by spontaneous imbibition derived from mathematical model and experiment |
分别对鄂尔多斯盆地延长组岩心3、岩心11、岩心21(参见表 1)进行渗吸模拟计算,得到渗吸采出程度与渗吸驱油速率随时间的变化曲线(图 7)。由于各岩心孔喉分布不同,渗吸采出程度及渗吸驱油速率也不同。岩心11大孔喉比例大,渗透率高,因此,初始渗吸驱油速率及渗吸采出程度最高。随着渗吸时间增加,渗吸驱油速率开始降低,并在渗吸约3 000 s后,岩心11渗吸采出程度小于岩心3。分析认为岩心3孔喉分布较为集中,其渗吸驱油速率在较长时间内比较稳定。岩心21始终保持较低的渗吸驱油速率,是由于其孔喉半径较小。同时,渗吸足够长时间后,岩心21的渗吸采出程度大于岩心11,从其孔喉分布图(参见图 2)中可以发现,岩心11小孔喉半径所占的比例大于岩心21。因此,可以推断岩心孔喉半径分布对岩心的渗吸驱油速率及渗吸采出程度有着一定的影响。对比各岩心孔隙分布与其渗吸驱油速率发现,在渗吸前期,半径较大的孔喉对岩心渗吸影响较大,随着岩心内孔喉半径及其占比的增大,岩心渗吸驱油速率及渗吸采出程度随之增大;在渗吸后期,半径较小的孔隙对岩心的渗吸影响较大,岩心渗吸驱油速率随岩心内小孔喉占比增大而减小。此外,岩心11渗吸驱油速率达到最大值后,渗吸驱油速率下降曲线并不光滑,渗吸驱油速率迅速下降后逐渐趋于平缓,但随后再次急剧下降(图 7)。分析认为岩心11孔喉分布范围广且不均匀,微纳米孔喉在各半径处均有着一定分布,因而渗吸驱油速率随孔喉分布变化而变化。
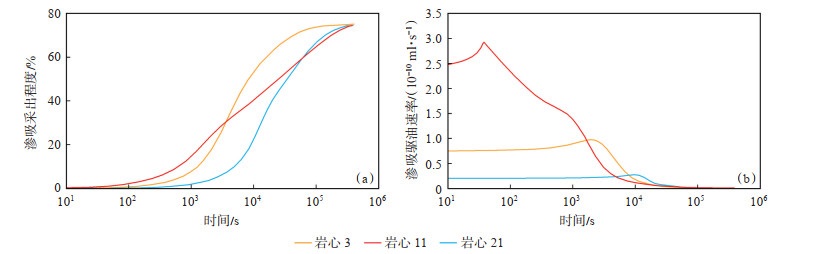
|
下载原图 图 7 不同孔喉结构类型致密岩心渗吸采出程度及渗吸驱油速率 Fig. 7 Oil recovery degree and imbibition rate in tight sandstone core samples with different pore throat size |
在相同时间内,随接触角增大,岩心的渗吸驱油速率明显降低,岩心的渗吸采出程度降低(图 8)。这是由于岩心接触角越小,岩心的亲水性越强,岩心毛管力越大,从而使得其在一定时间内有着较大的渗吸采出程度及渗吸驱油速率。当接触角接近90°时,岩心为中性润湿,毛管力几乎为0,因此其渗吸驱油速率几乎为0,并在渗吸较长时间后才开始产油。由此可知,增强岩心亲水性,可提高岩心渗吸驱油速率,使得岩心在短时间内保持着较高的渗吸驱油速率及渗吸采出程度。但当岩心为强水湿(θ < 30°)时,继续增强岩心亲水性,渗吸采出程度及渗吸驱油速率变化很小。
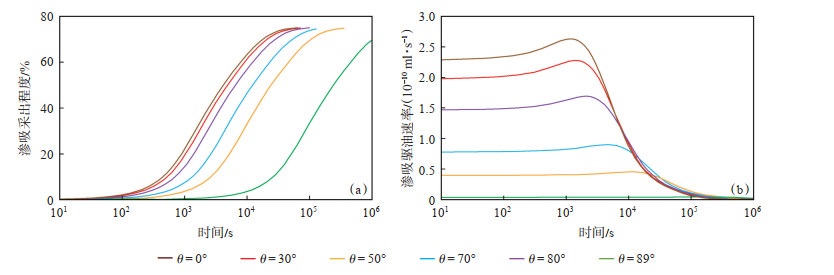
|
下载原图 图 8 不同润湿角下致密岩心渗吸采出程度及渗吸驱油速率 Fig. 8 Oil recovery degree and imbibition rate in tight sandstone core samples with different wetting angle |
随油水界面张力增大,在相同时间内,渗吸采出程度及渗吸驱油速率均增大,且油水界面张力越大,开始产油时间越早,渗吸驱油速率到达最大值所需时间越短(图 9)。由于表面活性剂能够改变岩石表面润湿性,因此其常被用于提高致密油藏渗吸驱油效果。表面活性剂在改变岩石润湿性的同时,会降低油水界面张力。油水界面张力降低会提高原油流动性,有助于启动残余油。但当油水界面张力过低时,渗吸的动力毛管力也会大幅度降低,不利于渗吸驱油的进行。因此,在筛选渗吸用表面活性剂时,所选表面活性剂在改变岩石润湿性的同时,需保持一定的的油水界面张力,超低界面张力不利于渗吸驱油的进行。
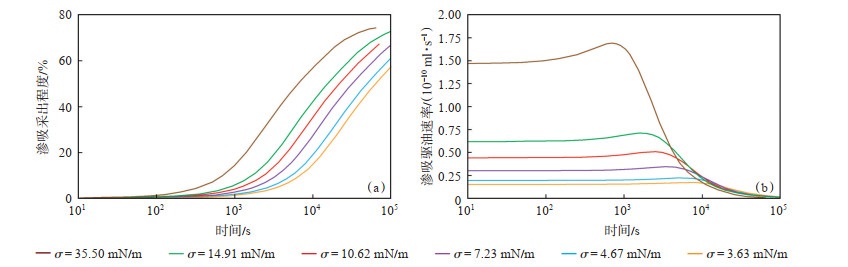
|
下载原图 图 9 不同界面张力下致密岩心渗吸采出程度及渗吸驱油速率 Fig. 9 Oil recovery degree and imbibition rate in tight sandstone core samples with different interfacial tensions |
保持水黏度不变,随着原油黏度从1 mPa·s增加至8 mPa·s,在相同时间内,渗吸采出程度[图 10(a)]及渗吸驱油速率[图 10(b)]均有着不同程度的下降。这是由于随着原油黏度的增加,黏滞阻力增大,从而使得原油渗吸驱油速率降低,渗吸采出程度下降。
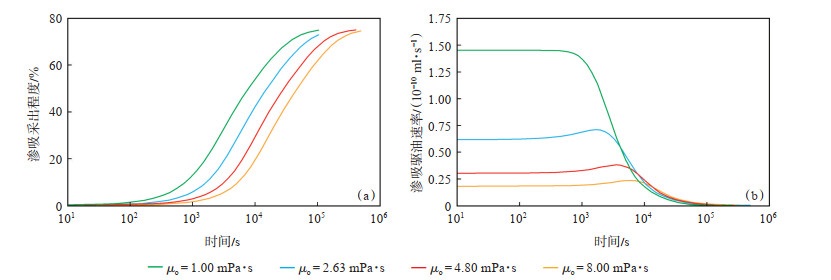
|
下载原图 图 10 不同原油黏度致密岩心渗吸采出程度及渗吸驱油速率 Fig. 10 Oil recovery degree and imbibition rate in tight sandstone core samples with different oil viscosities |
(1)在岩心孔喉分布频率dSHg/d(lg r)与孔喉半径对数lg r的半对数图上,致密砂岩孔喉分布具有二维高斯分布特征。基于二维高斯函数拟合得到孔喉分布可以准确地预测致密砂岩渗透率,可用于模拟计算致密砂岩渗吸驱油速率。
(2)在渗吸前期,渗吸驱油速率主要取决于最大孔喉半径与大孔喉分布占比,孔喉半径越大,渗吸驱油速率越快;在渗吸后期,渗吸驱油速率主要取决于中小孔喉。确定致密岩心孔喉分布特征能够有效预测岩心渗吸驱油速率,明确岩心渗吸规律,从而指导致密油藏的合理生产制度。
(3)岩心渗吸驱油速率受岩心润湿性、油水界面张力、原油黏度等因素影响。在致密油藏注水开发过程中,增强储层岩石的亲水性,保持一定的界面张力可以有效发挥渗吸驱油潜力,提高致密油藏开发效果。
| [1] |
徐立研, 王胡振, 张立韧, 等. 中国致密油研究现状及发展趋势. 当代化工, 2017, 46(1): 86-88. XU L Y, WANG H Z, ZHANG L R, et al. Research status and development trend of tight oil in China. Contemporary Chemical Industry, 2017, 46(1): 86-88. DOI:10.3969/j.issn.1671-0460.2017.01.026 |
| [2] |
慎迪. 中美致密油勘探开发对比与启示. 云南化工, 2018, 45(3): 87. SHEN D. Comparison and enlightenment of tight oil exploration and development between China and America. Yunnan Chemical Technology, 2018, 45(3): 87. |
| [3] |
刘淑波. 致密砂岩岩心纳米级孔喉结构分布特征研究. 中国石油大学胜利学院学报, 2018, 32(2): 21-23. LIU S B. Research on the distribution characteristics of nanometer pore throat structure in tight sandstone core. Journal of Shengli College China University of Petroleum, 2018, 32(2): 21-23. |
| [4] |
杜金虎, 何海清, 杨涛, 等. 中国致密油勘探进展及面临的挑战. 中国石油勘探, 2014, 19(1): 1-9. DU J H, HE H Q, YANG T, et al. Progress in China's tight oil exploration and challenges. China Petroleum Exploration, 2014, 19(1): 1-9. DOI:10.3969/j.issn.1672-7703.2014.01.001 |
| [5] |
师煜涵. 基于核磁共振研究压裂液在长7储层中的渗吸作用. 西安: 西安石油大学, 2018. SHI Y H. Study on fracturing fluid's imbibition of chang-7 source based on nuclear magnetic resonance. Xi'an: Xi'an Shiyou University, 2018. |
| [6] |
MIRZAEI-PAIAMAN A, MASIHI M, STANDNES D C. An analytic solution for the frontal flow period in 1d counter-current spontaneous imbibition into fractured porous media including gravity and wettability effects. Transport in Porous Media, 2011, 89(1): 49-62. DOI:10.1007/s11242-011-9751-8 |
| [7] |
CAI J, YU B, ZOU M, et al. Fractal characterization of spontaneous co-current imbibition in porous media. Energy & Fuels, 2010, 24(3): 1860-1867. |
| [8] |
WANG X, SHENG J J. Spontaneous imbibition analysis in shale reservoirs based on pore network modeling. Journal of Petroleum Science and Engineering, 2018, 169: 663-672. DOI:10.1016/j.petrol.2018.06.028 |
| [9] |
刘秀婵, 陈西泮, 刘伟, 等. 致密砂岩油藏动态渗吸驱油效果影响因素及应用. 岩性油气藏, 2019, 31(5): 114-120. LIU X C, CHEN X P, LIU W, et al. Influencing factors of dynamic imbibition displacement effect in tight sandstone reservoir and application. Lithologic Reservoirs, 2019, 31(5): 114-120. |
| [10] |
李斌会, 付兰清, 董大鹏, 等. 松辽盆地北部致密砂岩高温高压吞吐渗吸实验. 特种油气藏, 2018, 25(1): 1-7. LI B H, FU L Q, DONG D P, et al. High temperature-pressure huff-puff imbibition experiment in the tight sandstone reservoir of northern Songliao Basin. Special Oil and Gas Reservoirs, 2018, 25(1): 1-7. |
| [11] |
李洪, 李治平, 王香增, 等. 基于喉道分布特征的致密砂岩渗吸模型. 科学技术与工程, 2018, 18(13): 50-54. LI H, LI Z P, WANG X Z, et al. Imbibition model of tight sandstone based on distribution characteristics of roar. Science Technology and Engineering, 2018, 18(13): 50-54. |
| [12] |
谷潇雨, 王朝明, 蒲春生, 等. 裂缝性致密油藏水驱动态渗吸特征实验研究: 鄂尔多斯盆地富县地区长8储层为例. 西安石油大学学报(自然科学版), 2018, 33(3): 37-44. GU X Y, WANG C M, PU C S, et al. Experimental study on dynamic imbibition characteristics of fractured tight sandstone reservoir during water flooding: an example from Chang 8 reservoir of Fuxian area in Ordos Basin. Journal of Xi'an Shiyou University(Natural Science Edition), 2018, 33(3): 37-44. |
| [13] |
李爱芬, 何冰清, 雷启鸿, 等. 界面张力对低渗亲水储层自发渗吸的影响. 中国石油大学学报(自然科学版), 2018, 42(4): 67-74. LI A F, HE Q B, LEI Q H, et al. Influence of interfacial tension on spontaneous imbibition in low-permeability water-wet reservoirs. Journal of China University of Petroleum(Edition of Natural Science), 2018, 42(4): 67-74. |
| [14] |
XU D, BAI B, WU H, et al. Mechanisms of imbibition enhanced oil recovery in low permeability reservoirs: Effect of IFT reduction and wettability alteration. Fuel, 2019, 244: 110-119. |
| [15] |
MENG Q, LIU H, WANG J. A critical review on fundamental mechanisms of spontaneous imbibition and the impact of boundary condition, fluid viscosity and wettability. Advances in GeoEnergy Research, 2017, 1(1): 1-17. |
| [16] |
濮御, 王秀宇, 濮玲. 静态渗吸对致密油开采效果的影响及其应用. 石油化工高等学校学报, 2016, 29(3): 23-27. PU Y, WANG X Y, PU L. Effect of spontaneous imbibition on tight reservoirs. Journal of Petrochemical University, 2016, 29(3): 23-27. |
| [17] |
于馥玮, 苏航. 中国致密油特征与开发思路探索. 当代化工, 2015, 44(7): 1550-1552. YU F W, SU H. Characteristics and development technique research of tight oil in China. Contemporary Chemical Industry, 2015, 44(7): 1550-1552. |
| [18] |
印森林, 陈恭洋, 陈玉琨, 等. 砂砾岩储层孔隙结构模态控制下的剩余油分布-以克拉玛依油田七东1区克下组为例. 岩性油气藏, 2018, 30(5): 91-102. YIN S L, CHEN G Y, CHEN Y K, et al. Control effect of pore structure modality on remaining oil in glutenite reservoir: a case from lower Karamay Formation in block Qidong 1 of Karamay Oilfield. Lithologic Reservoirs, 2018, 30(5): 91-102. |
| [19] |
张新旺, 郭和坤, 李海波. 基于核磁共振致密油储层渗吸驱油实验研究. 科技通报, 2018, 34(8): 35-40. ZHANG X W, GUO H K, LI H B. Experimental study on imbibition oil displacement of tight oil reservoir using NMR technology. Bulletin of Science and Technology, 2018, 34(8): 35-40. |
| [20] |
濮御, 王秀宇, 杨胜来. 利用NMRI技术研究致密储层静态渗吸机理. 石油化工高等学校学报, 2017, 30(1): 45-48. PU Y, WANG X Y, YANG S L. Research on spontaneous imbibition mechanism of tight oil reservoirs using NMR method. Journal of Petrochemical University, 2017, 30(1): 45-48. |
| [21] |
韦青, 李治平, 王增香, 等. 裂缝性致密砂岩储层渗吸机理及影响: 鄂尔多斯盆地吴起地区长8储层为例. 油气地质与采收率, 2016, 4(23): 102-107. WEI Q, LI Z P, WANG X Z, et al. Mechanism and influence factors of imbibition in fractured tight sandstone reservoir: an example from Chang 8 reservoir of Wuqi area in Ordos Basin. Petroleum Geology and Recovery Efficiency, 2016, 4(23): 102-107. |
| [22] |
顾雅頔, 喻高明, 李桂姗. 低渗致密砂岩储层孔隙结构特征及自发渗吸实验. 科学技术与工程, 2019, 19(32): 139-145. GU Y D, YU G M, LI G S. Experimental of pore structure and spontaneous imbibition of low permeability tight sandstone reservoirs. Science Technology and Engineering, 2019, 19(32): 139-145. |
| [23] |
杨柳, 鲁晓兵, 葛洪魁, 等. 致密储层渗吸特征与孔径分布的关系. 科学技术与工程, 2019, 19(16): 106-111. YANG L, LU X B, GE H K, et al. The relationship between imbibition characteristics and pore size distribution. Science Technology and Engineering, 2019, 19(16): 106-111. |
| [24] |
WANG F, ZHAO J. A mathematical model for co-current spontaneous water imbibition into oil-saturated tight sandstone: Upscaling from pore-scale to core-scale with fractal approach. Journal of Petroleum Science and Engineering, 2019, 178: 376-388. |
| [25] |
杨胜来. 油层物理学. 北京: 石油工业出版社, 2004. YANG S L. Reservoir physics. Beijing: Petroleum Industry Press, 2004. |
| [26] |
WANG F, YANG K, YOU J, et al. Analysis of pore size distribution and fractal dimension in tight sandstone with mercury intrusion porosimetry. Results in Physics, 2019, 13: 102283. |
 2021, Vol. 33
2021, Vol. 33




