近年来,随着常规油气资源储量的减少以及油气勘探开发技术的提高,我国正持续加大以页岩气、致密气为代表的非常规油气资源的勘探开发力度[1-3]。不同于常规油气藏,页岩气藏富含微纳米级孔隙,孔渗条件差,基质孔隙度通常 < 12%,渗透率通常 < 1 mD[4]。目前,页岩气藏的商业开发主要依赖于通过大型水力压裂来尽可能沟通储层中发育的天然微裂缝。所以,开展气体在页岩储层中的渗流机理研究,对于页岩气藏的渗流理论研究及工程实践都具有重要意义。
由于页岩气藏独特的储层物性,页岩气的运移过程呈现出从分子尺度到宏观尺度的多尺度的特性。页岩气的流动机理包括了自由气在人工裂缝中的达西流动和在基质微孔隙中的连续流、滑脱流以及过渡流,吸附气在微孔隙表面吸附/解吸以及扩散[5]。通常对非常规裂缝性气藏渗流规律的研究手段主要有室内实验以及数值模拟方法[6-7]。由于非常规气藏超低孔、低渗的储层特性,对实验设备要求较高,流体的渗流过程也难以进行直观地观测,所以,通过数值方法模拟流体在多孔介质中的渗流方式得到广泛的应用。目前已有大量的用于表征气体在纳米级孔隙中运移的模型。此类模型主要分为2类:一类是基于Hagen-Poiseuille模型对其边界条件进行修正,从而表征页岩气的多种运移机制[8-10];另一类是按一定的权重系数对多种运移机制进行耦合并考虑气体分子间的相互作用建立的真实气体传输模型[11]。此类模型仅能用于描述页岩气在单一纳米孔隙中的运移规律,尚不能直接用于研究页岩气在天然微裂缝发育的复杂多孔介质中的运移特征。
格子Boltzmann方法(LBM)以其易于处理复杂几何边界问题、编程较简单等优势在近年来被大量用于非常规气藏微观渗流模拟研究[12-14]。LBM模拟分为孔隙尺度以及表征单元(REV)尺度,其中孔隙尺度主要用于模拟流体在微纳米尺度孔隙中的流动,而不能直接用于模拟流体在天然裂缝发育的多孔介质中的流动过程[15]。Guo等[16]通过在广义格子Boltzmann方程中添加修正项来实现孔隙尺度向REV尺度的升级。此后,该方法被大量运用于非常规油气藏渗流模拟。Zhao等[17]运用REV尺度的格子Boltzmann方法,模拟了气相在重构多孔介质中的渗流过程,并对多孔介质渗透率进行了计算。Zhao等[15]应用格子Boltzmann方法对页岩气在基质中的渗流过程进行了REV尺度的模拟,并对页岩气渗流规律的影响因素进行了分析。张烈辉等[18]基于页岩扫描电镜图像运用REV尺度的格子Boltzmann方法模拟了页岩气在单一天然微裂缝中的渗流。Zhang等[19]基于页岩扫描电镜建立的二值图像模拟了水相在富含有机质页岩多孔介质中的渗流过程,并通过在二值图像上规则排布天然裂缝的方式分析了天然裂缝的存在对页岩气藏渗流规律的影响。
本文首先重构天然微裂缝发育的页岩储层多孔介质模型,然后对Zhao等[15]以及Liu等[20]提出的格子Boltzmann模型围绕页岩气藏特性对演化方程以及边界条件进行针对性修正,并将其升级到REV尺度,使其能够表征页岩气在裂缝性多孔介质中滑脱、吸附/解吸以及气体扩散等运移机制;应用修正模型模拟气体在天然微裂缝发育的多孔介质中的流动过程;最后基于模拟结果对气体渗流特性以及渗透率影响因素进行分析,以期为页岩气藏的渗流规律研究提供新思路。
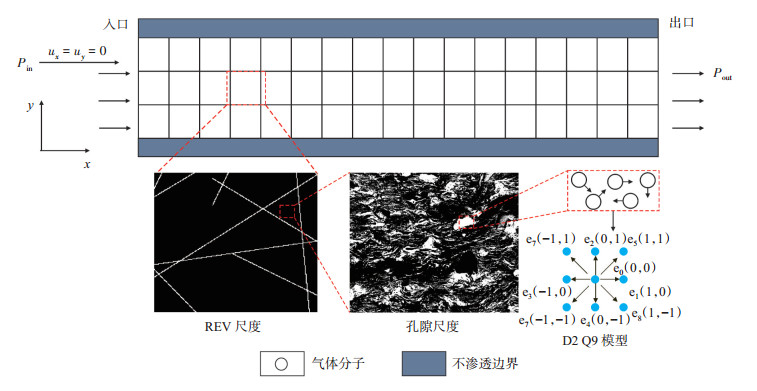
1 页岩气藏表征单元体尺度微观渗流模型 1.1 物理模型本文建立的页岩气藏渗流模拟流动域如图 1所示。整个渗流过程考虑二维流动,流场上、下均为不渗透边界;整个渗流过程为从入口处通过压力驱动从左至右的流动;气体渗流过程的速度分布用格子Boltzmann方法中的二维九速模型(D2 Q9)进行表征。由于模型的求解过程复杂,为了提高求解效率,对模型作出了如下假设:①流场中仅考虑甲烷气体的单相流动;②渗流过程为等温渗流过程;③对于天然微裂缝的物性参数仅考虑裂缝长度、裂缝宽度以及裂缝密度。
|
下载原图 图 1 低渗致密裂缝性气藏渗流场物理模型及气体分子D2 Q9模型速度分布 Fig. 1 Schematic of 2D physic model for simulating gas transport in naturally micro-fractured gas reservoir and the velocity directions of gas transport in D2 Q9 model |
本文使用LBM来表征气体在上述物理模型中的渗流过程。该方法是将Boltzmann方程进行离散,把流体分子运动分为迁移和碰撞等2个过程[21]。广义格子Boltzmann演化方程为
| $ {f_i}(x + {e_i}\Delta t,t + \Delta t) - {f_i}(x,t) = - \frac{1}{\tau }[{f_i}(x,t) - f_i^{eq}(x,t)] + \Delta t{F_i}(x,t),\quad i = 0,1, \cdots ,N $ | (1) |
式中:x为格子空间格点位置;t为格子空间的某一时刻;fi(x,t)为t时刻格子空间中x格点沿i方向的气体密度分布函数;Δt为格子空间的时间步长;τ为驰豫时间;Fi(x,t)为格子空间x格点沿i方向的外力项函数;ei为格子空间的离散速度。
ei在D2 Q9模型中气体分子的运动方向分为以下9个方向。
| $ {e_i} = \left\{ {\begin{array}{*{20}{l}} {(0,0),}&{i = 1}\\ {\left[ {{\rm{cos}}\frac{{(i - 1)\pi }}{2},{\rm{sin}}\frac{{(i - 1)\pi }}{2}} \right],}&{i = 2 \backsim 5}\\ {\left[ {{\rm{cos}}\frac{{(2i - 9)\pi }}{4},{\rm{sin}}\frac{{(2i - 9)\pi }}{4}} \right],}&{i = 6 \backsim 9} \end{array}} \right. $ | (2) |
式中:i为方向编号。
在式(1)中,fieq为平衡态分布函数,本文模型考虑多孔介质的非均质性,其表达式如下[22]:
| $ f_i^{eq}(x,t) = {\omega _i}\rho \left[ {1 + \frac{{u{e_i}}}{{c_{\rm{s}}^2}} + \frac{{{u^2}\left( {e_i^2 - c_{\rm{s}}^2I} \right)}}{{2\varphi c_{\rm{s}}^4}}} \right] $ | (3) |
式中:ωi为加权系数,取值为ω0 = 4/9,ω1 - 4 = 1/9,ω5 - 8 = 1/36;cs为格子空间声速,
驰豫时间对于LBM模型至关重要,由于在页岩气藏中,气体的流动特性由努森数(Kn)控制,所以对于驰豫时间必须进行相应的修正,其表达式[13]为
| $ {\tau _{\rm{e}}} = \frac{1}{2} + \sqrt {\frac{6}{\pi }} \frac{L}{{\Delta {\kern 1pt} x}}\frac{{Kn{\kern 1pt} \varphi (Kn){{(1 + 0.5b{\kern 1pt} \rho {\kern 1pt} \chi )}^2}}}{\chi } $ | (4) |
式中:L为流场特征长度,m;Δx格子尺寸,m;φ(Kn)为考虑努森层的修正函数,φ(Kn) =
χ的计算式为
| $ \begin{array}{l} \chi = 1 + \frac{5}{8}b\rho + 0.286{\kern 1pt} {\kern 1pt} {\kern 1pt} 9{(b\rho )^2} + 0.110{\kern 1pt} {\kern 1pt} {\kern 1pt} 3{(b\rho )^3} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.038{\kern 1pt} {\kern 1pt} {\kern 1pt} 6{(b{\kern 1pt} \rho )^4} \end{array} $ | (5) |
式中:b = 2 π d3/(3 m)。其中,d为甲烷分子直径,m;m为甲烷分子质量,kg。
气体的动力黏度也是影响渗流过程的重要参数,其在格子空间的计算式为
| $ \nu = c_{\rm{s}}^2\left( {{\tau _{\rm{e}}} - \frac{1}{2}} \right)\Delta {\kern 1pt} t $ | (6) |
式(1)中的格子空间外力项Fi考虑孔隙表面对于气体分子的作用,其离散形式为
| $ \begin{array}{*{20}{l}} {{F_i} = {\omega _i}{\kern 1pt} \rho \left( {1 - \frac{1}{{2{\tau _{\rm{e}}}}}} \right)\left[ {\frac{{{e_i}{\kern 1pt} F}}{{c_{\rm{s}}^2}} + \frac{{u{\kern 1pt} F(e_i^2 - c_{\rm{s}}^2)}}{{\varphi {\kern 1pt} c_{\rm{s}}^4}}} \right] + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} G{\kern 1pt} \varPhi (x,t)\sum\limits_i {{\omega _i}} (x + {e_i}\Delta t,t){e_i}} \end{array} $ | (7) |
式中:Φ(x, t)为势函数;F为格子空间气体分子所受总外力项。
F的计算式为
| $ F = - \frac{{\varphi {\kern 1pt} \nu }}{K}u - \frac{{\varphi {\kern 1pt} {F_\varepsilon }}}{{\sqrt K }}|u|u + \varphi {\kern 1pt} G $ | (8) |
式中:G为格子空间气体分子所受外部力,主要为基质及裂缝表面对气体分子的吸附力;Fε为几何形状因子;K为固有渗透率,m2。
Fε与K的计算式[23]为
| $ {F_\varepsilon } = \frac{{1.75}}{{\sqrt {150{\kern 1pt} {\varphi ^3}} }},K = \frac{{{\varphi ^3}d_{\rm{p}}^2}}{{150{{(1 - \varphi )}^2}}} $ | (9) |
式中:dp为平均孔隙直径,m。
气体的宏观密度以及速度可以通过下式进行计算
| $ {\rho = \sum\limits_{i = 0}^8 {{f_i}} (x,t)} $ | (10) |
| $ {\rho {\kern 1pt} u = \sum\limits_{i = 0}^8 {{e_i}} {f_i}(x,t) + \frac{{\Delta {\kern 1pt} t}}{2}\rho {\kern 1pt} F} $ | (11) |
由于式(8)中也包含流体流速u,所以要对式(8)进行求解,必须联立式(8)及式(11)
| $ u = \frac{V}{{{d_0} + \sqrt {d_0^2 + {d_1}|V|} }} $ | (12) |
V为临时变量,其计算式为
| $ V = \frac{{\sum\limits_{i = 0}^8 {{e_i}} {f_i}(x,t)}}{\rho } + \frac{{\Delta {\kern 1pt} t}}{2}\varphi {\kern 1pt} G $ | (13) |
联立式(12)及式(13)则可以得到气体宏观速度u的计算式为
| $ u = \frac{{\frac{{\sum\limits_{i = 0}^8 {{e_i}} {f_i}(x,t)}}{\rho } + \frac{{\Delta {\kern 1pt} t}}{2}\varphi G}}{{{d_0} + \sqrt {d_0^2 + {d_1}\left| {\frac{{\sum\limits_{i = 0}^8 {{e_i}} {f_i}(x,t)}}{\rho } + \frac{{\Delta {\kern 1pt} t}}{2}\varphi {\kern 1pt} G} \right|} }} $ | (14) |
d0及d1的完整表达式为
| $ {d_0} = \frac{1}{2}\left( {1 + \frac{{\Delta {\kern 1pt} t}}{2}\frac{{\varphi {\kern 1pt} v}}{K}} \right),{d_1} = \frac{{\Delta {\kern 1pt} t}}{2}\frac{{\varphi {\kern 1pt} {F_\varepsilon }}}{{\sqrt K }} $ | (15) |
本文模型考虑了页岩气藏中气体吸附/解吸及扩散效应,所以必须对传统的格子Boltzmann方法的边界条件进行修正。岩石表面的气体滑移流动速度的表达式[24]为
| $ {u_{\rm{s}}} = (1 - \alpha ){u_{\rm{g}}} + \alpha {\kern 1pt} {u_{\rm{w}}} $ | (16) |
式中:ug为离边界层最近的气流速度,m/s;uw为假定的固体表面速度,m/s;α为比例系数。
表征的气体在孔隙及裂缝表面的吸附情况,可由下式进行计算
| $ \alpha = \frac{{{C_{\rm{ \mathsf{ μ} }}}}}{{{C_{{\rm{ \mathsf{ μ} }}{\kern 1pt} {\rm{max}}}}}} = \frac{{\frac{P}{{{P_{\rm{L}}}}}}}{{1 + \frac{P}{{{P_{\rm{L}}}}}}} $ | (17) |
式中:Cμ及Cμmax分别为吸附气浓度及最大吸附浓度,g/m3;PL为兰格缪尔压力,MPa。
式(16)中的uw为假定的边界滑移速度,在页岩气藏须要考虑气体的吸附以及表面扩散作用,其表达式为
| $ {u_{\rm{w}}} = \frac{{{D_{\rm{S}}}}}{{{D_{\rm{K}}}{\rho _{\rm{a}}}}}\left[ {{\rho _{\rm{g}}}{u_{\rm{g}}}\frac{{k{\rho _{{\rm{ \mathsf{ μ} }}{\kern 1pt} {\rm{max}}}}}}{{{{(1 + k\rho )}^2}}}} \right] $ | (18) |
式中:DK为气体分子扩散系数,m2/s;DS为气体表面扩散系数,m2/s。
在格子空间s可由下式进行计算[25]:
| $ {D_{\rm{S}}} = C_{\rm{S}}^2({\tau _{\rm{e}}} - 0.5)\Delta {\kern 1pt} t $ | (19) |
Guo等[23]提出了对REV尺度的格子Boltzmann模型的验证方法,后来该方法被大量应用于REV尺度格子Boltzmann模型准确性的验证[15, 19-20]。本文也选取该方法对所建模型的准确性进行验证。
首先设置模型上、下不渗透平板间的多孔介质孔隙度为20%,流体在模型入口处受到恒定的压力驱动,其流动过程满足Brinkman达西方程
| $ \frac{{{\nu _{\rm{e}}}}}{\varphi }\frac{{{\partial ^2}u}}{{\partial {\kern 1pt} {y^2}}} - \frac{\nu }{K}u + G = 0 $ | (20) |
其解析解为
| $ u = \frac{{G{\kern 1pt} K}}{\nu }\left\{ {1 - \frac{{{\rm{cosh}}\left[ {\frac{{a(y - H)}}{2}} \right]}}{{{\rm{cosh}}\left( {\frac{{a{\kern 1pt} H}}{2}} \right)}}} \right\} $ | (21) |
式中:
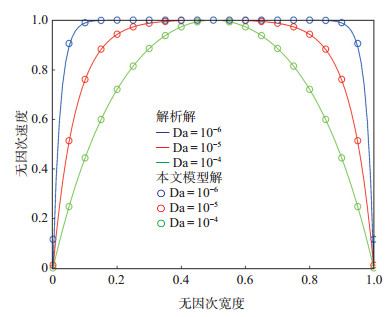
格子空间中的一些必要参数取值为:网格数Lx × Ly = 100 × 100,流体密度ρ = 1,黏度ν = 1/6,驱动压差ΔP = 1。图 2为不同达西数下的解析解与本文所建立模型的数值解的对比。从图 2可看出,本文模型的计算结果与经典解析解吻合,证明了本文所建立的REV尺度格子Boltzmann模型(LB模型)具有较高的准确性。
|
下载原图 图 2 不同达西数下不渗透平板间的无因次速度剖面 Fig. 2 Velocity profiles of fluid flow between two plates under different Darcy number |
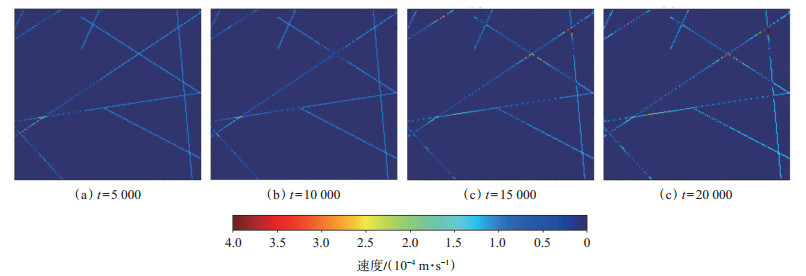
本文模型模拟所用的基本参数及其格子空间尺度向真实物理空间尺度的转换关系如表 1所列。在LBM中主要通过保持格子空间和物理空间流动特征数不变的准则来实现尺度的转换。将表 1中的参数带入本文所建立的LB模型中,然后通过编程求解可以得到气体在重构页岩基质多孔介质中的渗流动态。图 3展示了在不同时间步长下的气体流速分布情况。从图 3可以看出,当天然裂缝较发育时,大量气体沿天然裂缝窜进,天然裂缝沟通程度越显著时气流速度越大。以上结论证实了天然裂缝发育及储层中天然裂缝的沟通作用对于页岩气藏开发十分重要。
|
|
下载CSV 表 1 模型基本参数 Table 1 Parameters used for simulation |
|
下载原图 图 3 不同时间步长下的气流速度分布情况 Fig. 3 Gas velocity distribution under different time steps |
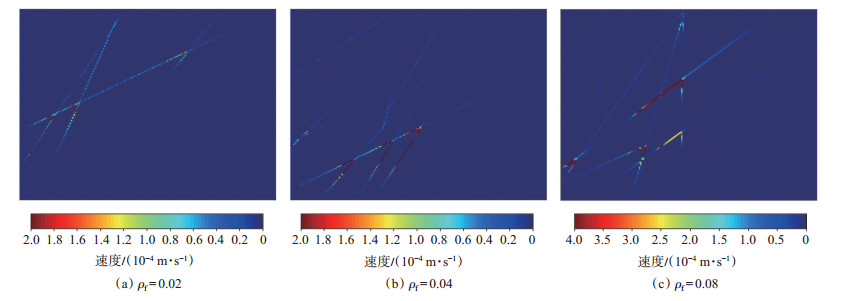
为了进一步明确天然微裂缝对于页岩气藏气体渗流特性的影响,图 4展示了不同裂缝密度下(ρf= 0.02,0.04,0.08)的气体流速分布情况。在3种模拟条件下,仅改变裂缝的线密度、裂缝宽度Wf =(2~ 4)×10-6 m,裂缝长度lf =(1~4)×10-4 m、裂缝倾角θ = 0°~60°,其余流体参数保持表 1中的数值不变。从图 4可以看出,当裂缝密度增大时,气体流动通道增加,渗流能力显著增强。
|
下载原图 图 4 不同裂缝密度下气体流速分布云图 Fig. 4 Distributions of gas velocity under different fracture density |
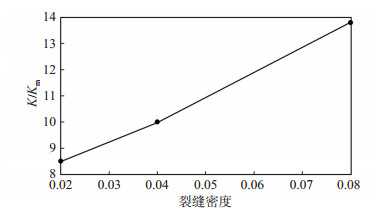
图 5为不同天然裂缝密度条件下,所建立裂缝性多孔介质的表观渗透率与基质固有渗透率比值的变化情况。从图 5可以看出,随着天然裂缝密度的增加,表观渗透率将显著增大。
|
下载原图 图 5 不同裂缝密度下的表观渗透率增大倍数 Fig. 5 Apparent permeability increase multiple under different fracture density |
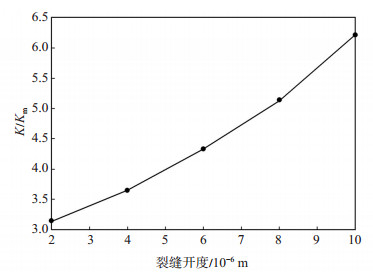
同样仅改变裂缝开度,保持天然裂缝ρf = 0.04及lf=(1~4)×10-4 m不变,将裂缝参数以及流体参数带入LB模型,计算所得表观渗透率的增大情况如图 6所示。从图 6可以看出,随着裂缝开度的增加,表观渗透率增量会随之增大。这是由于天然裂缝开度增加后,气体在天然裂缝的流动通道增大,从而引起气体表观渗透率增大。
|
下载原图 图 6 不同裂缝开度下的表观渗透率增大倍数 Fig. 6 Apparent permeability increase multiple under different fracture aperture |
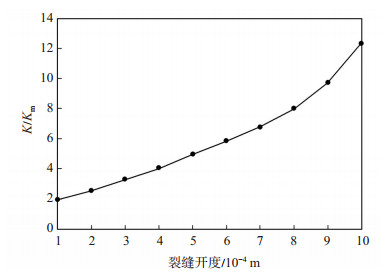
仅改变裂缝长度,保持其他裂缝参数为ρf= 0.04及Wf =(2~4)×10-6 m不变,同样将上述裂缝参数及流体物性参数带入本文LB模型进行计算,得到表观渗透率增大倍数情况如图 7所示。从图 7可以看出,随着裂缝长度的增加,表观渗透率的增大倍数也随之增加。对比裂缝宽度对于表观渗透率增大量的贡献,裂缝长度对于表观渗透率的增大作用更为显著。这是由于随着裂缝长度的增加,基质向裂缝的窜流会加剧,从而引起表观渗透率的大幅上升。
|
下载原图 图 7 不同裂缝长度下的表观渗透率增大倍数 Fig. 7 Apparent permeability increase multiple under different fracture length |
在页岩气藏中,气体运移规律不同于常规储层。为了进一步明确页岩储层中气体多重运移的规律,有必要对气体渗流特征参数进行敏感性分析。
当储层致密,气体渗流通道狭窄时,气体分子自由程将接近于其流动通道的特征长度,此时Kn对于气体流动的影响将加剧。气体在页岩储层中的流动可由Kn的大小将其划分为4种流态[26]。其中Kn ≤ 0.001为连续介质流;0.001 < Kn ≤ 0.100为滑脱流;0.1 < Kn ≤ 10.0为过渡流;Kn > 10为自由分子流。为了能够定量分析Kn对于气体流动特征的影响,笔者模拟了Kn为0.007,0.069,0.687条件下的气体渗流过程。
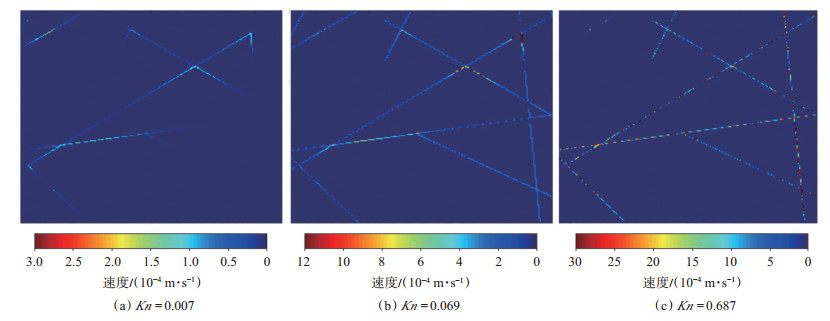
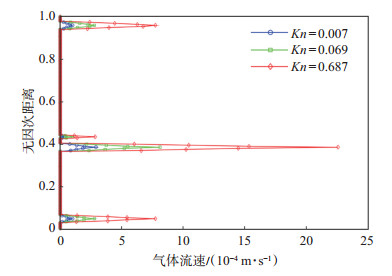
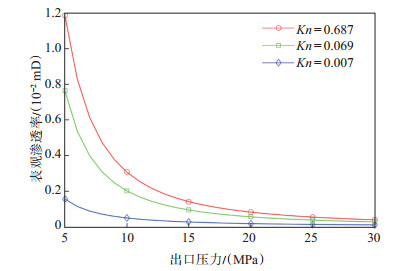
图 8表明,随着Kn的增大,气体流动过程中克氏效应越显著,气体流速也随之增大。为了能够直观观测Kn对于气体渗流速度的影响,图 9展示了不同Kn下的气体流速剖面。从图 9可看出,当Kn持续增大后,裂缝壁面的滑脱效应更加显著,使得气体沿天然微裂缝窜进的速度大幅提升;特别是当Kn > 0.1时,流态进入过渡流后,气体流速增幅显著变大。图 10为不同Kn下的裂缝性多孔介质表观渗透率随出口压力的变化情况。从图 10可以看出,随着Kn的增大,表观渗透率也随之增大;特别是当Kn > 0.1时,表观渗透率增幅明显增大。
|
下载原图 图 8 不同Kn下的气体流速分布云图 Fig. 8 Distribution of gas velocity under different Kn |
|
下载原图 图 9 不同Kn下的气体流速剖面 Fig. 9 Profiles of gas velocity magnitude under different Kn |
|
下载原图 图 10 不同Kn下的表观渗透率随出口压力的变化情况 Fig. 10 Variance of apparent permeability with the rising outlet pressure under different Kn |
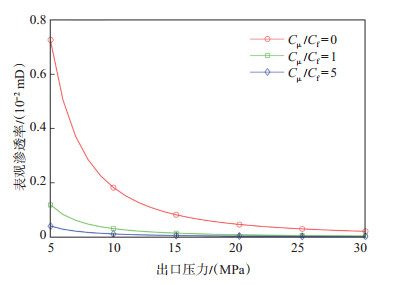
页岩气藏中气体的吸附/解吸对于气体渗流有巨大的影响。为了能够直观表征气体吸附/解吸作用对于页岩气藏表观渗透率的影响,本文计算了不同吸附气量下多孔介质的表观渗透率。图 11为不同吸附气浓度下表观渗透率的变化情况。从图 11可以看出,随着吸附气量的增加,多孔介质的表观渗透率随之下降。出现该结果的主要原因是由于在页岩有机质中,吸附气吸附在孔隙表面会占据部分游离气的流动通道,使基质的有效孔隙减小,从而影响气体的渗流[27]。
|
下载原图 图 11 不同吸附气浓度下的表观渗透率变化情况 Fig. 11 Variance of apparent permeability under different adsorption strength |
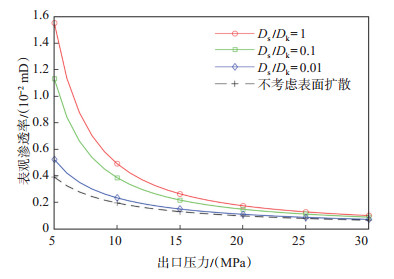
目前,大量研究表明[28-30],页岩气藏有机质中吸附气的表面扩散作用是影响页岩气渗流过程的关键因素。在本文模型中,气体表面扩散作用的强弱是通过表面扩散系数Ds来进行表征。图 12为不同表面扩散系数比值下(Ds/Dk = 0,0.01,0.1,1),页岩气藏多孔介质表观渗透率随压力的变化情况。从图 12可以看出,在压力较低的情况下,考虑气体表面扩散效应的表观渗透率数值较不考虑表面扩散效应的情况能够提升2~5倍。这样的模拟结果表明气体表面扩散效应对于表观渗透率的贡献作用是不可忽略的。
|
下载原图 图 12 不同表面扩散系数下的表观渗透率变化情况 Fig. 12 Variance of apparent permeability under different surface diffusivity |
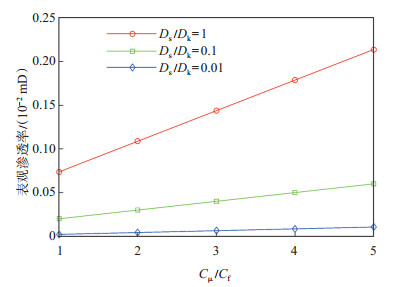
在页岩有机质中,气体表面扩散效应并不能无限变化,其强弱受制于吸附气量的多少。所以,表面扩散系数以及吸附气量是影响页岩气表面扩散效应的2个关键参数。图 13为考虑不同表面扩散效应下,多孔介质表观渗透率随吸附气量的变化情况。从图 13可以看出,表面扩散效应对表观渗透率的贡献会随着吸附气量的增大而增加,吸附气量越大时,不同表面扩散系数对表观渗透率的影响也愈发显著。
|
下载原图 图 13 不同表面扩散系数下的表观渗透率随吸附气量增长的变化情况 Fig. 13 Variance of apparent permeability with ascending adsorbed gas concentration under different surface diffusivity |
(1) 重构了天然微裂缝发育的页岩储层多孔介质,考虑页岩气渗流过程中的滑脱、吸附/解吸、表面扩散效应等运移机制对广义格子Boltzmann模型进行了修正,并基于经典REV尺度格子Boltzmann模型验证方法对重构模型的正确性进行了验证。
(2) 应用重构模型对页岩气渗流过程进行了模拟。结果表明,当储层天然微裂缝较发育时,绝大部分气体沿天然微裂缝窜进,天然微裂缝成为页岩气渗流的主要通道。通过对天然微裂缝物性参数进行敏感性分析发现,裂缝密度对于页岩气渗流的促进作用最为显著;随着裂缝密度增大3~4倍,储层表观渗透率可增大10倍以上;裂缝长度及裂缝开度对表观渗透率的贡献则较小。
(3) 参数敏感性分析表明,努森数(Kn)是影响页岩气渗流特征的主要参数,随着Kn的增大,克氏效应显著,气体流速随之增大,特别当Kn > 0.1时,表观渗透率增幅明显增大;表观渗透率会随着吸附气量的增大而减小,特别当储层压力较低时,该现象更为显著;表面扩散效应也是影响页岩气渗流的主要因素之一,同等条件下考虑气体表面扩散效应的表观渗透率较忽略该因素可提升2~5倍,但提升作用受制于吸附气量的多少。
| [1] |
郑珊珊, 刘洛夫, 汪洋, 等. 川南地区五峰组-龙马溪组页岩微观孔隙结构特征及主控因素. 岩性油气藏, 2019, 31(3): 55-65. ZHENG S S, LIU L F, WANG Y, et al. Characteristics of microscopic pore structures and main controlling factors of WufengLongmaxi Formation shale in southern Sichuan Basin. Lithologic Reservoirs, 2019, 31(3): 55-65. |
| [2] |
王登, 余江浩, 赵雪松, 等. 四川盆地石柱地区自流井组页岩气成藏条件与勘探前景. 岩性油气藏, 2020, 32(1): 27-35. WANG D, YU J H, ZHAO X S, et al. Accumulation conditions and exploration potential of shale gas of Ziliujing Formation in Shizhu area, Sichuan Basin. Lithologic Reservoirs, 2020, 32(1): 27-35. |
| [3] |
罗群, 吴安彬, 王井伶, 等. 中国北方页岩气成因类型、成气模式与勘探方向. 岩性油气藏, 2019, 31(1): 1-11. LUO Q, WU A B, WANG J L, et al. Genetic types, generation models, and exploration direction of shale gas in northern China. Lithologic Reservoirs, 2019, 31(1): 1-11. |
| [4] |
MA Y S, CAI X Y, ZHAO P R. China's shale gas exploration and development:Understanding and practice. Petroleum Exploration and Development, 2018, 45(4): 589-603. |
| [5] |
吴克柳, 陈掌星. 页岩气纳米孔气体传输综述. 石油科学通报, 2016, 1(1): 91-127. WU K L, CHEN Z X. Review of gas transport in nanopores in shale gas reservoirs. Petroleum Science Bulletin, 2016, 1(1): 91-127. |
| [6] |
姜瑞忠, 张福蕾, 崔永正, 等. 考虑应力敏感和复杂运移的页岩气藏压力动态分析. 岩性油气藏, 2019, 31(4): 149-156. JIANG R Z, ZHANG F L, CUI Y Z, et al. Pressure dynamic analysis of shale gas reservoirs considering stress sensitivity and complex migration. Lithologic Reservoirs, 2019, 31(4): 149-156. |
| [7] |
余川, 周洵, 方光建, 等. 地层温压条件下页岩吸附性能变化特征:以渝东北地区龙马溪组为例. 岩性油气藏, 2018, 30(6): 10-17. YU C, ZHOU X, FANG G J, et al. Adsorptivity of shale under the formation temperature and pressure:a case of Longmaxi Formation in northeastern Chongqing. Lithologic Reservoirs, 2018, 30(6): 10-17. |
| [8] |
CIVAN F, RAI C S, SONDERGELD C H. Shale-gas permeability and diffusivity inferred by improved formulation of relevant retention and transport mechanisms. Transport in Porous Media, 2011, 86(3): 925-944. |
| [9] |
CIVAN F, RAI C S, SONDERGELD C H. Determining shale permeability to gas by simultaneous analysis of various pressure tests. SPE Journal, 2012, 17(3): 717-726. |
| [10] |
CHEN X J, YAO G Q. An improved model for permeability estimation in low permeable porous media based on fractal geometry and modified Hagen-Poiseuille flow. Fuel, 2017, 210: 748-757. |
| [11] |
吴克柳, 李相方, CHEN Z X. 页岩气纳米孔真实气体传输模型. 中国科学:技术科学, 2016, 46(1): 68-78. WU K L, LI X F, CHEN Z X. Real gas transport through nanopores of shale gas reservoirs. Scientia Sinica Technologica, 2016, 46(1): 68-78. |
| [12] |
FATHI E, AKKUTLU I Y. Lattice Boltzmann method for simulation of shale gas transport in kerogen. SPE Journal, 2013, 18(1): 27-37. |
| [13] |
姚军, 赵建林, 张敏, 等. 基于格子Boltzmann方法的页岩气微观流动模拟. 石油学报, 2015, 36(10): 1280-1289. YAO J, ZHAO J L, ZHANG M, et al. Microscale shale gas flow simulation based on Lattice Boltzmann method. Acta Petrolei Sinica, 2015, 36(10): 1280-1289. |
| [14] |
申林方, 王志良, 李邵军. 基于格子博尔兹曼方法表征体元尺度土体细观渗流场的数值模拟. 岩土力学, 2015, 36(增刊2): 689-694. SHEN L F, WANG Z L, LI S J. Numerical simulation for mesoscopic seepage field of soil based on lattice Boltzmann method at REV scale. Rock and Soil Mechanics, 2015, 36(Suppl 2): 689-694. |
| [15] |
ZHAO J Z, FU D Y, LI Y M, et al. REV-scale simulation of gas transport in shale matrix with lattice Boltzmann method. Journal of Natural Gas Science and Engineering, 2018, 57(1): 224-237. |
| [16] |
GUO Z L, ZHAO T S. Lattice Boltzmann model for incompressible flows through porous media. Physical Review E, 2002, 66(3): 162-173. |
| [17] |
ZHAO T Y, ZHAO H W, NING Z F, et al. Permeability prediction of numerical reconstructed multiscale tight porous media using the representative elementary volume scale lattice Boltzmann method. International Journal of Heat and Mass Transfer, 2018, 118(1): 368-377. |
| [18] |
张烈辉, 贾鸣, 郭晶晶. 基于REV尺度格子Boltzmann方法的页岩气流动数值模拟. 力学与实践, 2017, 39(2): 130-134. ZHANG L H, JIA M, GUO J J. Numerical simulation of shale gas flow based on the lattice Boltzmann method at REV scale. Mechanics in Engineering, 2017, 39(2): 130-134. |
| [19] |
ZHANG T, LI X F, WANG X Z, et al. Modelling the water transport behavior in organic-rich nanoporous shale with generalized lattice Boltzmann method. International Journal of Heat and Mass Transfer, 2018, 127(1): 123-134. |
| [20] |
LIU L J, YAO J, ZHANG L, et al. REV-scale simulation of microfractured unconventional gas reservoir. Journal of Natural Gas Science and Engineering, 2017, 48(1): 100-110. |
| [21] |
LIU X H, LIU H, LIU Y Z. Theory and application of lattice Boltzmann method. Applied Mechanics and Materials, 2011, 79(1): 270-275. |
| [22] |
REN J J, GUO P, GUO Z L, et al. A lattice Boltzmann model for simulating gas flow in Kerogen pores. Transport in Porous Media, 2015, 106(2): 285-301. |
| [23] |
GUO Z L, SHU C. Lattice Boltzmann method and its applications in engineering. Singapore: World Scientific, 2013.
|
| [24] |
FATHI E, TINNI A, AKKUTLU I Y. Correction to Klinkenberg slip theory for gas flow in nano-capillaries. International Journal of Coal Geology, 2012, 103(23): 51-59. |
| [25] |
ZHOU L, QU Z G, CHEN L, et al. Lattice Boltzmann simulation of gas-solid adsorption processes at pore scale level. Journal of Computational Physics, 2015, 300(1): 800-813. |
| [26] |
ROY S, RAJU R, CHUANG H F, et al. Modeling gas flow through microchannels and nanopores. Journal of Applied Physics, 2003, 93(8): 4870-4879. |
| [27] |
朱汉卿, 贾爱林, 位云生, 等. 基于氩气吸附的页岩纳米级孔隙结构特征. 岩性油气藏, 2018, 30(2): 77-84. ZHU H Q, JIA A L, WEI Y S, et al. Nanopore structure characteristics of shale based on Ar adsorption. Lithologic Reservoirs, 2018, 30(2): 77-84. |
| [28] |
SHENG M, LI G S, HUANG Z W, et al. Pore-scale modeling and analysis of surface diffusion effects on shale-gas flow in Kerogen pores. Journal of Natural Gas Science and Engineering, 2015, 27(4): 979-985. |
| [29] |
李冬冬, 张艳玉, 孙晓飞, 等. 考虑表面扩散的实际状态页岩气表观渗透率新模型. 中国石油大学学报(自然科学版), 2018, 42(4): 82-90. LI D D, ZHANG Y Y, SUN X F, et al. A new model for assessing apparent permeability of shale gas at real gas condition considering surface diffusion. Journal of China University of Petroleum(Edition of Natural Science), 2018, 42(4): 82-90. |
| [30] |
吴克柳, 李相方, 陈掌星. 页岩气有机质纳米孔气体传输微尺度效应. 天然气工业, 2016, 36(11): 51-64. WU K L, LI X F, CHEN Z X. Micro-scale effects of gas transport in organic nanopores of shale gas reservoirs. Natural Gas Industry, 2016, 36(11): 51-64. |
 2020, Vol. 32
2020, Vol. 32



