2. 西南石油大学 石油与天然气工程学院, 成都 610500
2. School of Petroleum Engineering, Southwest Petroleum University, Chengdu 610500, China
地层测试技术是油气勘探中及时发现油气层,防止漏掉油气层的一个重要环节,也被称为“临门一脚”工程。由于深水复杂环境和放喷过程中地层到井筒、井筒内流体流动的复杂性[1-3],须要分析放喷过程中井筒内油气瞬态流动状态及规律,以便为确定合理测试工作制度提供依据[4]。
目前,对深水气井测试放喷主要利用稳态模型来进行计算分析,但测试工况明显是快瞬态问题,采用稳态模型或简化为慢瞬态问题明显存在误差。国内外对深水气井测试工艺制度、深水油气井传热及气井开关井的模拟研究较广泛,但未考虑地层流入、井筒流动规律、地面油嘴流动等瞬态流动过程响应[5]。鉴于深水放喷测试中,缺乏对实际放喷过程中井筒内流态、压力、温度变化的准确认识[6-9],无法合理确定诱喷关键参数。
为此,将放喷过程分为测试液位上升和地层产气等2个阶段,首次将地层流动、井筒流动及地面嘴流耦合,结合两相嘴流模型、两相持液率模型、地层产能方程、深水瞬态传热模型,建立深水放喷井筒瞬态流动模型,较稳态模拟结果更能真实反映开井测试过程,量化分析不同时间下沿井筒剖面压力、温度、持液率等关键参数变化规律,开展油嘴、管柱敏感性分析,以期为深水气井测试工艺设计、后续跟踪评价提供分析手段。
1 测试放喷阶段温压场耦合模型 1.1 井筒两相流压降瞬态模型建立测试放喷过程的井筒流动为不稳定两相流动,为此建立油气井开井放喷过程井筒气液两相压力瞬态模型。模型假设如下:油管中视为一维气液两相不稳定管流;气相视为可压缩流体,液相视为不可压缩流体;放喷测试过程气井产量较高,视为气液均质流动;沿井筒流动方向向上规定为z轴的正方向。
根据质量守恒、动量守恒原理得到控制方程为
| $ \frac{{\partial {\kern 1pt} {\kern 1pt} {\rho _{\rm{m}}}}}{{\partial {\kern 1pt} {\kern 1pt} t}} + \frac{{\partial {\kern 1pt} {\kern 1pt} {G_{\rm{m}}}}}{{\partial {\kern 1pt} {\kern 1pt} z}} = 0 $ | (1) |
| $ \frac{{\partial {\kern 1pt} {\kern 1pt} {G_{\rm{m}}}}}{{\partial {\kern 1pt} {\kern 1pt} t}} + {\kern 1pt} {\kern 1pt} \frac{{\partial {\kern 1pt} {\kern 1pt} {G_{\rm{m}}}}}{{\partial {\kern 1pt} {\kern 1pt} z}}\left( {\frac{{G_{\rm{m}}^2}}{{{\rho _{\rm{m}}}}}} \right) + \frac{{\partial {\kern 1pt} {\kern 1pt} p}}{{\partial {\kern 1pt} {\kern 1pt} z}} + {\rho _{\rm{m}}}{\kern 1pt} g{\kern 1pt} {\kern 1pt} {\rm{sin}}{\kern 1pt} {\kern 1pt} \theta + \frac{{{f_{\rm{m}}}{G_{\rm{m}}}|{G_{\rm{m}}}|}}{{2D{\rho _{\rm{m}}}}} = 0 $ | (2) |
式中:ρm为气液混合物密度,kg/m3;t为时间,s;Gm为两相流单位面积质量流量,kg/(m2·s);z为井深,m;p为井筒压力,Pa;fm为两相流摩阻系数;θ为井斜角,(°);g为重力加速度,m/s2;D为管径,m。
考虑到深水气井测试放喷产气量较高,因此在气液两相流瞬态模拟中将井筒流动简化为气液均质流动。采用Rendeiro等[10]对产液气井气体相对密度同时进行含油与含水的修正,计算混合物相对密度和密度修正如下:
| $ {{\gamma _{\rm{m}}} = \frac{{{\gamma _{\rm{g}}} + \frac{{817.7{\kern 1pt} {\gamma _{\rm{L}}}}}{{G{\kern 1pt} L{\kern 1pt} R}}}}{{1 + \frac{{200}}{{G{\kern 1pt} L{\kern 1pt} R}}}}} $ | (3) |
| $ {{\rho _{\rm{m}}} = \frac{{28.96{\gamma _{\rm{m}}}p}}{{{Z_{\rm{m}}}R{\kern 1pt} T}}} $ | (4) |
式中:γm为混合物相对密度;γg为气相相对密度;γL为液相相对密度;GLR为气液比,m3/m3;Zm为混合物偏差系数;R为气体常数,取值8 315,Pa·m3·kmol-1· K-1;T为温度,K。
其中天然气偏差系数Zm可采用Dranchuk等[11]关系式迭代计算
| $ \begin{array}{l} {Z_{\rm{m}}} = \left( {{A_1} + \frac{{{A_2}}}{{{T_{{\rm{pr}}}}}} + \frac{{{A_3}}}{{T_{{\rm{pr}}}^3}} + \frac{{{A_4}}}{{T_{{\rm{pr}}}^4}} + \frac{{{A_5}}}{{T_{{\rm{pr}}}^5}}} \right){\rho _{\rm{r}}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {{A_6} + \frac{{{A_7}}}{{{T_{{\rm{pr}}}}}} + \frac{{{A_8}}}{{T_{{\rm{pr}}}^2}}} \right)\rho _{\rm{r}}^2 - {A_9}\left( {\frac{{{A_7}}}{{{T_{{\rm{pr}}}}}} + \frac{{{A_8}}}{{T_{{\rm{pr}}}^2}}} \right)\rho _{\rm{r}}^5 + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {A_{10}}(1 + {A_{11}}\rho _{\rm{r}}^2)\left( {\frac{{\rho _{\rm{r}}^2}}{{T_{{\rm{pr}}}^3}}} \right){\rm{exp}}( - {A_{11}}\rho _{\rm{r}}^2) + 1.0 \end{array} $ | (5) |
式中:A1-A11为模型系数;ρr为拟对比密度;Tpr为拟对比温度。
1.2 调产过程井筒温度瞬态模型建立在真实放喷测试过程中,由于生产和试井测试的需要,产量往往不是定值,需要调产,甚至频繁调产[12-16],此时采用单一产量下的温度瞬态模型无法模拟频繁调产下的温度变化,造成压力计算误差大,会导致拟合失败。为提高对真实放喷测试过程的拟合精度,必须推导调产工况下的井筒温度瞬态叠加公式。
1.2.1 产量调增当t1时刻产量从Q1调增到Q2时,假定t1时刻的温度为T1,须要模拟t2时刻的温度T2。此时可以采用温度叠加原理,关键是假设产量Q2在t1时刻之前存在一个虚拟初始升温时刻,该时刻与t1时刻的间隔为Δt1,据稳态温度传热模型,Q1,Q2对应的稳态流温分别为T1,stable和T2,stable[图 1(a)]。

|
下载原图 图 1 产量调增(a)和调减(b)示意图 Fig. 1 Schematic diagram of increasing(a)and reducing(b)transient superposition |
基于井筒单位长度控制体的能量守恒原理,建立了井筒流体温度瞬态方程,然而该方程隐式差分形式复杂、计算量大、收敛难。为此,通过引入Ismadi等[17]研究得出的储热系数,结合井筒稳态温降基本方程,得到了计算井筒流体瞬态温度的显式方程,在保证计算精度的同时,提高了运算速度和可靠性。
于是温度T1可按下式计算
| $ \frac{{{T_1} - {T_{{\rm{ei}}}}}}{{{T_{{\rm{1, stable }}}} - {T_{{\rm{ei}}}}}} = 1 - {e^{ - a{\kern 1pt} {\kern 1pt} {t_1}}} $ | (6) |
式中:Tei为初始井筒静态温度,K;a为拟合系数。
虚拟时间间隔Δt1由下式计算
| $ \frac{{{T_1} - {T_{{\rm{ei}}}}}}{{{T_{{\rm{2 stable }}}} - {T_{{\rm{ei}}}}}} = 1 - {e^{ - a{\kern 1pt} {\kern 1pt} \Delta {t_1}}} $ | (7) |
即
| $ \Delta {t_1} = - \frac{1}{a}{\rm{ln}}\frac{{{T_{{\rm{2, stable }}}} - {T_1}}}{{{T_{{\rm{2, stable }}}} - {T_{{\rm{ ei }}}}}} $ | (8) |
于是t2时刻的温度T2可按下式计算
| $ \frac{{{T_2} - {T_{{\rm{ei}}}}}}{{{T_{{\rm{2, stable }}}} - {T_{{\rm{ei}}}}}} = 1 - {{\rm{e}}^{ - a({t_2} - {t_1} + \Delta {t_1})}} $ | (9) |
当t1时刻产量从Q1调减到Q2时,假设t1时刻的温度为T1,须要模拟t2时刻的温度T2。此时将产量Q2分解为“0+Q2”,即分解为如下2个过程:产量由Q1降为0 m3/d的关井过程和产量由0 m3/d增至Q2的开井过程。据稳态温度传热模型,Q1,Q2对应的稳态流温分别为T1,stable和T2,stable [图 1(b)]。
于是关井过程的t2时刻的温度变化值ΔT2,close可按下式计算
| $ \frac{{\Delta {T_{{\rm{2, close }}}}}}{{{T_1} - {T_{{\rm{ ei }}}}}} = {{\rm{e}}^{ - {a^\prime }({t_2} - {t_1})}} - 1 $ | (10) |
产量由0 m3/d增至Q2的开井过程温度变化值ΔT2,open可按下式计算
| $ \frac{{\Delta {T_{{\rm{2, open }}}}}}{{{T_{{\rm{2, stable }}}} - {T_{{\rm{ ei }}}}}} = 1 - {{\rm{e}}^{ - a({t_2} - {t_1})}} $ | (11) |
最终t2时刻的温度T2可按下式叠加计算
| $ \begin{array}{l} {T_2} = {T_1} + \Delta {T_{{\rm{2, open }}}} + \Delta {T_{{\rm{2, close }}}} = \\ \ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {T_{{\rm{2, stable }}}} - ({T_{{\rm{2, stable }}}} - {T_1}){{\rm{e}}^{ - a({t_2} - {t_1})}} \end{array} $ | (12) |
开井放喷以前,井筒中为静气柱和静液柱,流体温度为环境静温;开井放喷后,井口流体先流动,井底流体后流动,井筒呈现变质量流,并呈现气液两相流,地层中的气体和液体开始持续进入井筒,流体在上升过程中不断向地层和海水放热;当放喷达一段时间后,将进入稳定流动阶段[18-19](图 2)。

|
下载原图 图 2 开井放喷过程井筒流动示意图 Fig. 2 Schematic diagram of wellbore flow during blowout stage |
综合以上物理现象,构建了开井放喷井筒两相流瞬态模型,由井筒瞬态质量守恒、动量守恒、能量守恒组成,并且考虑了井筒流动与井口节流、地层产能的耦合[20-25],设置2个测试放喷流动阶段(图 3)。

|
下载原图 图 3 开井液位上升及地层流体驱替示意图 Fig. 3 Schematic diagram of liquid level rising and formation fluid displacement |
(1)阶段1为液位上升阶段。假设开井放喷以前,井筒呈现“上部静气柱(诱喷液)、下部静液柱”或井筒内充满液柱的分布特征。开井放喷后,若上部存在气柱并泄压,液位开始上升,地层液进入井筒。因此瞬态模型由“井口嘴流+气柱管流+液柱管流+地层渗流”耦合而成,其中多相嘴流公式采用适合亚临界流的Sachdeva等[26]模型嘴流公式。
(2)阶段2为地层产气阶段。井筒由液相变为两相流,持液率逐渐降低。其中,气液两相通过油嘴临界压力为
| $ {p_{\rm{r}}} = {\left\{ {\frac{{\frac{k}{{k - 1}} + \frac{{(1 - {x_{\rm{g}}})(1 - {p_{\rm{r}}}){\nu _{\rm{L}}}}}{{{x_g}{\nu _{{\rm{G1}}}}}}}}{{\frac{k}{{k - 1}} + \frac{n}{2} + \frac{{n(1 - {x_{\rm{g}}}){\nu _{\rm{L}}}}}{{{x_{\rm{g}}}{\nu _{{\rm{G2}}}}}} + \frac{n}{2}{{\left[ {\frac{{n(1 - {x_{\rm{g}}}){\nu _{\rm{L}}}}}{{{x_{\rm{g}}}{\nu _{{\rm{G2}}}}}}} \right]}^2}}}} \right\}^{\frac{k}{{k - 1}}}}\quad n = \frac{{1 + {x_{{\rm{G1}}}}({c_p} - {c_v})}}{{{x_{{\rm{G1}}}}{c_v} + (1 - {x_{{\rm{G1}}}}){c_1}}} $ | (13) |
式中:xg为混合物中气相质量分数,%;νL,νG1分别为嘴子入口处液相、气相比容,m3/kg;cp,cν分别为气体的定压、定容比热,J/(kg·K);c1为液相比热容,J/(kg·K)。
2 深水气井测试放喷阶段瞬态流动模拟 2.1 温压场耦合模型适用性分析为验证该模型的适用性,选取深水测试气井A井进行验证。该井位水深约为1 455 m,主力目的层位于黄流组,其压力系数为1.21,地层压力约40 MPa,温度梯度为3.87 ℃/100 m;海底泥线温度为3~4 ℃,预测井底温度约为95 ℃。采用“APR+ TCP”测试管柱下深到3 351 m,主体采用114.3 mm油管,即油管内径为76.2 mm,油管外径为114.3 mm。放喷前井筒中充满测试液与诱喷液。
利用深水测试放喷瞬态流动模拟程序对该井放喷初期进行模拟。其中气井产能采用指数式方程描述,产能方程系数C取1.2万m3/d·MPa-2n,指数n取0.75,模拟时间间隔为0.2 h,模拟时间为12 h。海水段井筒总传热系数取典型值45 W/(m2·℃),地层段井筒总传热系数取典型值20 W/(m2·℃),无因次储热系数取典型值5,地层导热系数取典型值4.2 W/(m·℃)。如图 4所示,利用模拟程序对该井的井身参数与环境参数进行分段,将井口至海底泥面井段分为10段,海底泥面至目的层井段分为10段,分段整理后得到温度结果;已知该井放喷前地层压力为40 MPa,关井井口压力为1.5 MPa,气体相对密度为0.6,测试液和诱喷液平均相对密度约为1.16,对井筒压力剖面进行计算,得到井筒内液位压力分布。

|
下载原图 图 4 环境温度插值及压力剖面处理结果 Fig. 4 Interpolation result of ambient temperature and wellbore pressure profile |
该井通过改变油嘴工作制度进行放喷作业。依据实际测试工况,对该井放喷期间的井筒压力、温度、产气量、持液率、水合物形成温度等影响参数进行模拟研究。如图 5所示,模拟的井筒压力、温度、产气量与实测值吻合较好,开井后8 640 s井口压力开始上升,此时井筒内外工作液开始被储层产出气体驱替,气液两相界面不断上移;约14 400 s时,井口持液率为0,井筒内工作液已被完全驱替,气相充满井筒,与实际情况吻合,模型计算的井口压力、温度与实际工况所测参数之间平均误差小于5%,满足计算精度要求。

|
下载原图 图 5 测试诱喷阶段关键参数模拟 Fig. 5 Simulation of key parameters in initial blowout |
由于初始环境泥线处温度最低,随着地层气体产出,井筒内温度不断升高,但通过模拟发现清井结束时泥线处井筒温度略低于水合物形成温度,因此泥线是水合物形成的风险点(图 6)。通过现场作业实测温度,也证明了该模拟结果,并在作业中注入水合物抑制剂。

|
下载原图 图 6 放喷初期水合物形成温度模拟 Fig. 6 Simulation of hydrate formation temperature at the initial blowout stage |
利用瞬态模拟程序对不同时间井筒压力、温度沿井深的分布进行预测,开井后井筒测试液被气流置换,井筒压力梯度降低,井口压力逐渐升高;开井后产气量逐渐增大,将地热带至井口,致使井筒温度逐渐升高(图 7)。

|
下载原图 图 7 A井放喷初期井筒温度、压力剖面预测图 Fig. 7 Profile prediction of wellbore temperature and pressure at the initial blowout stage of well A |
对持液率、密度沿井深的分布进行预测,开井后井筒测试液被气流置换,持液率和混合物密度不断降低,最终形成雾状流(图 8)。

|
下载原图 图 8 A井放喷初期持液率、密度分布曲线图 Fig. 8 Distribution curves of liquid holdup and density at the initial blowout stage of well A |
对水合物形成温度沿井深的分布进行预测(图 9)。泥线处环境温度仅为4℃,为全井筒最低温度,易形成水合物。该井放喷期间井筒温度随时间逐渐升高,最终泥线温度大于水合物形成温度,但在清井结束时,泥线温度是低于水合物形成温度的,有冰堵的风险,而该井由于事前向管柱中加入了甲醇,防止了水合物冰堵。该例亦说明了向管柱中加注水合物抑制剂的必要性。

|
下载原图 图 9 A井放喷初期水合物形成温度剖面预测 Fig. 9 Prediction of hydrate formation temperature profile at the initial blowout stage of well A |
(1)油嘴尺寸的影响
清井设计中,油嘴尺寸是一个重要的工艺参数。不同尺寸的油嘴对清井时间和地面设备要求及流程都有较大的影响。如图 10所示,分别选择3 mm,6 mm,9 mm,12 mm,15 mm油嘴进行敏感性分析,油嘴越大,产气量越高,清井速度越快,泥线温度越高;应尽量选择大于10 mm的油嘴,提高清井速度的同时,快速提高泥线温度,防止冰堵。

|
下载原图 图 10 油嘴尺寸敏感性参数影响 Fig. 10 Influence of nozzle size sensitivity parameters |
(2)油管尺寸的影响
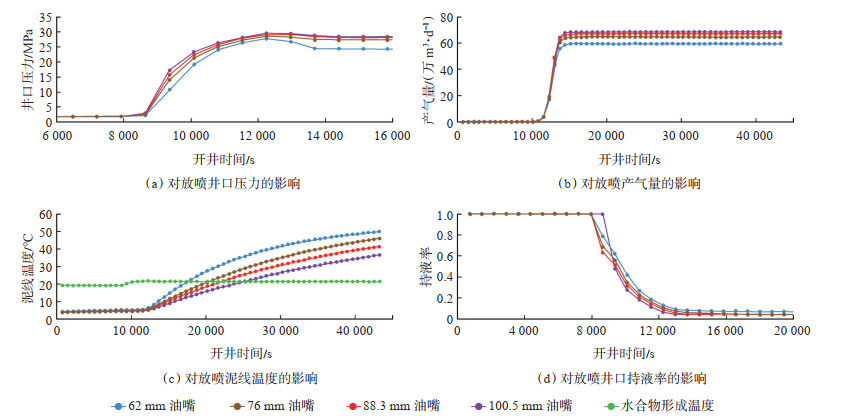
基于该井基础数据,选择内径分别为62 mm,76 mm,88.3 mm,100.5 mm的油管进行敏感性分析(图 11)。油管管径越大,摩阻越小,产气量越高,清井速度越快,但受流速减小的影响,泥线温度上升速度会变慢,为提高清井速度,建议选择管径较大的油管放喷,减小摩阻压降。
|
下载原图 图 11 油管尺寸敏感性参数影响 Fig. 11 Influence of tubing size sensitivity parameters |
B井为一口直井,水深815 m,设计完钻井深4 429.3 m,该井为常规温度压力系统,泥线温度为5 ℃,地温梯度为4 ℃/100 m,地层压力系数为1.00~ 1.15。该井初期诱喷液到达井口,模拟时间间隔为0.2 h,模拟时间为12 h。海水段井筒总传热系数取典型值25 W/(m2·℃),地层段井筒总传热系数取典型值15 W/(m2·℃),无因次储热系数取典型值5,地层导热系数取典型值4.2 W/(m·℃)。采用12 mm油嘴放喷,对其测试放喷过程进行瞬态模拟。基于以上假设条件,对该井放喷期间的井筒压力、温度、产气量、持液率、质量流速、水合物形成温度进行模拟(图 12)。该井放喷初期井筒压力先增后降,根据预测该井最终达到45万m3/d产量,清井时间约4 320 s,泥线温度将随着气体的产出而增加,但是在清井结束时泥线温度可能临近于水合物的形成温度,因此推荐在实际作业时测试液中加入水合物抑制剂。

|
下载原图 图 12 B井测试诱喷阶段关键参数预测 Fig. 12 Prediction of key parameters at the initial blowout stage of well B |
(1)首次将地层流动、井筒流动及地面嘴流耦合,结合两相嘴流模型、两相持液率模型、地层产能方程、深水瞬态传热模型,建立了深水放喷井筒瞬态流动模型,模型考虑了瞬态流动特征,较稳态模拟结果更能反映放喷测试过程,可合理确定放喷测试时间及测试制度。
(2)该深水气井测试温压场耦合模型可用于模拟放喷期间井筒液位、压力、温度、产气量、持液率、水合物形成温度随时间和井深的变化。通过模拟深水测试气井A井表明,计算压力、温度、持液率等结果与测试现场所获参数基本吻合,平均误差小于5%,满足计算精度要求;针对深水气井B井进行测试工作制度模拟,获得关键参数变化趋势。
(3)深水气井测试设计中,油嘴尺寸是一个重要的工艺参数。在满足测试作业要求下,应尽快调整油嘴,加快工作液清喷及地层流体产出速度,尤其应提高井筒泥线处温度,防止水合物生成。
(4)分析井筒内测试液及诱喷液垫对清井诱喷造成的影响,开井后井筒测试液被气流置换,井筒压力梯度降低,井口压力逐渐升高;随着产气量的增加,井底流压逐渐降低;井筒温度则随着开井时间的延长而增加,这是由于地热被带至井口所致,温度的稳定往往需要若干小时。因此,须要在保障管柱设备安全、稳定的前提下,设定合理的诱喷液垫高度。
| [1] |
王跃曾, 唐海雄, 陈奉友. 深水高产气井测试实践与工艺分析. 石油天然气学报(江汉石油学院学报), 2009, 31(5): 148-151. WANG Y Z, TANG H X, CHEN F Y. Test practice and process analysis of high production gas wells in deep water. Journal of Oil and Gas Technology(Journal of Jianghan Petroleum Institute), 2009, 31(5): 148-151. |
| [2] |
何吉祥, 段永刚, 何玉发. 深水测试设计影响因素分析. 油气井测试, 2013, 22(2): 67-69. HE J X, DUAN Y G, HE Y F. Influencing factor to design of the deep water well test. Well Testing, 2013, 22(2): 67-69. DOI:10.3969/j.issn.1004-4388.2013.02.022 |
| [3] |
鹿克峰, 简洁, 张彦振, 等. 井筒变流量气井携液临界流量的确定方法:以东海西湖凹陷多层合采气井为例. 岩性油气藏, 2017, 29(3): 147-151. LU K F, JIAN J, ZHANG Y Z, et al. A new method of measuring critical liquid carrying flow rate in the variable wellborerate gas well:a case of multi-completion gas wells in Xihu Sag, the East China Sea. Lithologic Reservoirs, 2017, 29(3): 147-151. DOI:10.3969/j.issn.1673-8926.2017.03.018 |
| [4] |
周雪梅, 段永刚, 何玉发, 等. 深水气井测试流动保障研究. 石油天然气学报(江汉石油学院学报), 2014, 36(5): 149-153. ZHOU X M, DUAN Y G, HE Y F, et al. The flow assurance of deep water gas-well testing. Journal of Oil and Gas Technology (Journal of Jianghan Petroleum Institute), 2014, 36(5): 149-153. |
| [5] |
陈欢, 李紫晗, 曹砚锋, 等. 临兴致密气井井筒积液动态模拟分析. 岩性油气藏, 2018, 30(2): 154-160. CHEN H, LI Z H, CAO Y F, et al. Dynamic simulation analysis of wellbore liquid loading in gas well for Linxing gas field. Lithologic Reservoirs, 2018, 30(2): 154-160. |
| [6] |
张崇, 任冠龙, 董钊, 等. 深水气井测试井筒温度场预测模型的建立及应用. 中国海上油气, 2016, 28(5): 78-84. ZHANG C, REN G L, DONG Z, et al. Establishment and application of a wellbore temperature field prediction model for deep water gas well testing. China Offshore Oil and Gas, 2016, 28(5): 78-84. |
| [7] |
EZZATTY N N, SHADA I H, KHAZALI-ROSLI K A, et al. Managing wellbore pressures by modeling of narrow margin deep water exploration well in Malaysia. SPE 189254, 2017.
|
| [8] |
高永海, 孙宝江, 王志远, 等. 深水钻探井筒温度场的计算与分析. 中国石油大学学报(自然科学版), 2008, 32(2): 58-62. GAO Y H, SUN B J, WANG Z Y, et al. Calculation and analysis of wellbore temperature field in deep water drilling. Journal of China University of Petroleum(Edition of Natural Science), 2008, 32(2): 58-62. DOI:10.3321/j.issn:1673-5005.2008.02.012 |
| [9] |
KABIR C S, YI X, JAKYMEC M, et al. Interpreting distributedtemperature measurements gathered in deep water gas-well testing. SPE 166333, 2013.
|
| [10] |
RENDEIRO C M, KELSO C M. An investigation to improve the accuracy of calculating bottom hole pressures in flowing gas wells producing liquids. SPE 17307, 1988.
|
| [11] |
DRANCHUK P M, ABOU-KASSEM H. Calculation of z factors for natural gases using equations of state. Journal of Canadian Petroleum, 1975, 14(3): 33-36. |
| [12] |
CURTIS M R, WITTERHOLT E J. Use of the temperature log for determining flow rates in producing wells. SPE 4637, 1973.
|
| [13] |
JOHNSON D, SIERRA J, KAURA D, et al. Successful flow profiling of gas wells using distributed temperature sensing data. SPE 103097, 2006.
|
| [14] |
KABIR C S, IZGEC B, HASAN A R, et al. Computing flow profiles and total flow rate with temperature surveys in gas wells. Journal of Natural Gas Science & Engineering, 2011, 4: 1-7. |
| [15] |
ISMADI D, KABIR C S, HASAN A R. The use of combined static and dynamic-material-balance methods with real-time surveillance data in volumetric gas reservoirs. SPE Reservoir Evaluation & Engineering, 2012, 15(3): 351-360. |
| [16] |
IZGEC B, KABIR C S, ZHU D, et al. Transient fluid and heat flow modeling in coupled wellbore/reservoir systems. SPE Reservoir Evaluation & Engineering, 2007, 10(3): 294-301. |
| [17] |
ISMADI D, KABIR C S, HASAN A R. The use of combined static-and dynamic-material-balance methods with real-time surveillance data in volumetric gas reservoirs. SPE Reservoir Evaluation & Engineering, 2012, 15(3): 351-360. |
| [18] |
何玉发, 李紫晗, 高飞, 等. 深水气井测试清井诱喷瞬态流动模拟. 天然气工业, 2018, 38(11): 59-64. HE Y F, LI Z H, GAO F, et al. Transient flow simulation on the induced flow in well cleaning during deep water gas well tests. Natural Gas Industry, 2018, 38(11): 59-64. DOI:10.3787/j.issn.1000-0976.2018.11.007 |
| [19] |
吴木旺, 杨红君, 梁豪, 等. 基于临界流量的深水探井测试关键技术与实践:以琼东南盆地深水区为例. 天然气工业, 2015, 35(10): 65-70. WU M W, YANG H J, LIANG H, et al. Key techniques and practices of critical flow based tests for deep water exploration wells:a case study of deep water area in the Qiongdongnan Basin. Natural Gas Industry, 2015, 35(10): 65-70. DOI:10.3787/j.issn.1000-0976.2015.10.008 |
| [20] |
IZGEC B, HASAN A R, LIN D, et al. Flow rate estimation from wellhead-pressure and temperature data. SPE 115790, 2008.
|
| [21] |
SARKER S, MOELEKER P, CHIN G, et al. Optimizing operational performance of riser systems through improved understanding of riser thermal behavior. IPTC 17185, 2013.
|
| [22] |
CHURCHILL S W, CHU H H S. Correlating equations for laminar and turbulent free convection from a vertical plate. International Journal of Heat and Mass Transfer, 1975, 18(11): 1323-1329. DOI:10.1016/0017-9310(75)90243-4 |
| [23] |
周赵川, 王辉, 代向辉, 等. 海上采油井筒温度计算及隔热管柱优化设计. 石油机械, 2014, 42(4): 43-48. ZHOU Z C, WANG H, DAI X H, et al. Calculation of offshore oil production wellbore temperature and optimal design of heatproof string. China Petroleum Machinery, 2014, 42(4): 43-48. DOI:10.3969/j.issn.1001-4578.2014.04.011 |
| [24] |
鲁港, 李新强, 杨兆臣, 等. 井筒热损失计算的改进算法. 特种油气藏, 2006, 13(3): 99-101. LU G, LI X Q, YANG Z C, et al. Improved algorithm of wellbore heat loss calculation. Special Oil and Gas Reservoirs, 2006, 13(3): 99-101. DOI:10.3969/j.issn.1006-6535.2006.03.033 |
| [25] |
于继飞, 吴晓东, 韩国庆, 等. 海上油井井口温度计算方法探讨. 中国海上油气, 2009, 21(5): 332-337. YU J F, WU X D, HAN G Q, et al. The discussion about how to calculate offshore wellhead temperature. China Offshore Oil and Gas, 2009, 21(5): 332-337. DOI:10.3969/j.issn.1673-1506.2009.05.010 |
| [26] |
SACHDEVA R, SCHMIDT Z, BRILL J P. Two-phase flow through chocks. SPE 15657, 1986.
|
 2020, Vol. 32
2020, Vol. 32




