目前,渤海L油田综合含水率达90%,已经步入高含水阶段,传统的沉积微相研究已经不能满足开发的需要。对于曲流河沉积的储层而言,点坝内部侧积层控制的剩余油分布逐渐成为挖潜的主要目标[1-4]。因此,开展基于曲流河储层构型的矢量注采结构调整是有效挖潜剩余油的关键。
在现今储层构型及油藏注采结构调整研究中,国内外学者都进行了相关研究,但主要集中在储层构型模式[5-7]、点坝内部侧积层分布[8-14]及对剩余油分布的影响上[15-22],而储层构型与油藏注采结构调整相结合的研究较少,特别是在研究点坝内部侧积层的基础上对注采结构进行调整的方法较为缺乏。为此,以渤海L油田河流相储层为例,在储层构型精细解剖的基础上,建立曲流河储层构型概念模型,结合数值模拟方法研究侧积层产状对流体运动的控制作用,并根据油藏工程方法推导考虑储层构型控制作用的水驱波及系数表达式。最终,建立曲流河储层构型控制下的注采结构矢量调整图版,提出基于曲流河储层构型的注采结构矢量调整技术,以期为储层构型内部剩余油精细挖潜提供依据。
1 研究区概况渤海L油田位于渤中凹陷北部石臼坨凸起中部,其为在新近系古隆起背景上发育的大型低幅度披覆背斜构造,主要目的层段为明化镇组下段和馆陶组,其中明化镇组下段为曲流河沉积[23-24],储层展布复杂,岩性以中-细砂岩及粉砂岩为主。经过15 a的生产开发,油田已进入高含水开发阶段,采油速度低,自然递减大,油藏水驱开发效果不均,导致油田平面矛盾突出,很难得到有效挖潜。
传统以复合砂体为研究单元的方式,已不能满足渤海L油田生产开发的需求,而砂体内部的储层构型解剖成为油田开发后期的突破重点。因此,须要研究不同储层构型模式对油藏注水开发的影响,从而制定有效的调整策略。
2 曲流河储层构型及控制作用储层构型模式是反映储层与内部构型单元的几何形态、规模、方向及其相互关系的抽象表述。自Miall[5-6]提出构型要素分析方法以后,中外很多学者以现代沉积为指导,结合野外露头进一步发展了曲流河点坝内部侧积体与泥质侧积层的识别方法及沉积理论,并建立了水平斜列式[25]、阶梯斜列式[26]和波浪式[27]等3种曲流河点坝构型模式。
研究储层构型模式是储层构型表征的基础,只有通过建立不同的构型模式才能够预测地下储层的构型分布[28-32],从而研究不同井网井型部署的开发效果,预测剩余油的分布状况。
2.1 砂体构型模式研究在沉积过程中,伴随着曲流河的不断侧向加积或改道形成了不同的河道带,且曲流河的侧向加积过程会形成点坝,点坝内部包含多个侧积体及侧积层。研究点坝内部侧积层的倾角、厚度、分布频率(侧积层个数)、水平宽度等产状参数是曲流河储层精细解剖的关键。
陆上油田通过对比小井距的测井资料(井距小于100 m),可以有效描述点坝内部侧积层的产状。海上油田受成本制约,不具备陆上油田小井距的条件,不能完全照搬陆上油田的做法,但是海上油田能够采集到更高品质的地震资料,通过建立沉积微相与波阻抗之间的对应关系可以克服海上油田大井距的缺点,并利用距离相对较近的“对子井”进行储层构型解剖[24]。
通过分析渤海L油田22对“对子井”的资料,确定渤海L油田南区明化镇组下段Ⅰ油组曲流河储层构型模式,并认为该区点坝中的侧积层主要为水平斜列式分布。结合Leeder[33]经验公式,确定渤海L油田南区Ⅰ油组点坝内部的构型参数(表 1)。
|
|
下载CSV 表 1 渤海L油田南区明化镇组下段I油组曲流河储层构型参数 Table 1 Meandering river reservoir architecture parameters of N1 ml in southern Bohai L oilfield |
油井的生产过程可以看作地下流体在能量差异的作用下经过不同的储层构型模式流动到生产井的过程。注采井网内油井的生产状况可以大致反映储层构型模式对流体运动的控制作用,而不同的储层构型模式对流体运动的控制作用是不同的。研究注采井网在不同储层构型模式下的生产状况,搞清储层构型模式对流体运动的控制作用显得尤为重要。
油井日产液状况是地下流体在能量差异作用下经过不同储层构型模式流动到井筒的直接体现。因此,将受储层构型影响的油井日产液与基准地层(均质地层或不含侧积层的地层)油井日产液的比值α定义为储层构型模式对流体运动的控制系数,且不同的储层构型模式具有不同的控制系数α,其表达式为
| $ \alpha = \frac{{{Q_{受构型影响}}}}{{{Q_{基准}}}} $ | (1) |
式中:Q受构型影响为受储层构型影响下的油井日产液,m3/d;Q基准为受基准地层影响下的油井日产液,m3/d;α为储层构型模式对流体运动的控制系数。
根据Q=νA,而生产井的射孔段长度为定值,则不同储层构型模式的控制作用只会体现在流体的运动速度上,即
| $ {v_{受构型影响}} = \alpha {v_{基准}} $ | (2) |
式中:ν受构型影响为受储层构型影响下的流体运动速度,m/d;ν基准为受基准地层影响下的流体运动速度,m/d。
根据达西定律,储层构型模式控制下的油水两相稳定渗流的运动方程为
| $ {v_{受构型影响}} = \alpha K\left[ {\frac{{{K_{{\text{ro}}}}\left( {{S_{\text{w}}}} \right)}}{{{\mu _{\text{o}}}}} + \frac{{{K_{{\text{rw}}}}\left( {{S_{\text{w}}}} \right)}}{{{\mu _{\text{w}}}}}} \right]\frac{{\partial p}}{{\partial r}} $ | (3) |
式中:K为地层绝对渗透率,mD;μo为地层原油黏度,mPa·s;μw为地层水黏度,mPa·s;Kro(Sw)为目前含水饱和度对应的油相相对渗透率;Krw(Sw)为目前含水饱和度对应的水相相对渗透率;p为地层压力,MPa。
根据式(3)可以确定储层构型模式对地层流体运动的控制作用,其主要体现在对地层渗透能力的影响上,同一地区的地层渗透能力会因为储层构型模式的不同而发生改变,即不同的储层构型模式会对地层渗透率产生不同的影响效果,从而对地下流体运动起控制作用。因此,受储层构型影响下的地层渗透能力表达式为
| $ {K_{受构型影响}} = \alpha {K_{基准}} $ | (4) |
式中:K受构型影响为受储层构型影响下的地层渗透率,mD;K基准为受基准地层影响下的地层渗透率,mD。
因此,研究不同储层构型模式对流体运动的控制系数,对研究不同储层构型模式下的地层渗透能力具有重要意义。
2.3 砂体构型模式的控制系数渤海L油田南区明化镇组下段Ⅰ油组主要为曲流河沉积,通过对该区曲流河储层进行精细解剖,明确了各级次构型单元的空间形态、规模、叠置组合关系,为三维储层构型建模提供了数据支撑。
通过PETREL建模软件,建立曲流河储层构型机理模型,以此研究不同储层构型模式对流体运动的控制作用。设计模型为油水两相,无气顶。模型中储层的厚度、渗透率、孔隙度、饱和度等参数与流体参数均选自渤海L油田南区I油组实测数据。按上述条件建立曲流河点坝基准模型[图 1(a)],并在模型中设计2口直井(1口生产井与1口注水井)。令生产井与注水井定压生产一段时间,其方案编号设为F0。在基准模型的基础上添加曲流河储层构型模式中的侧积层,建立曲流河点坝构型模型[图 1(b)]。
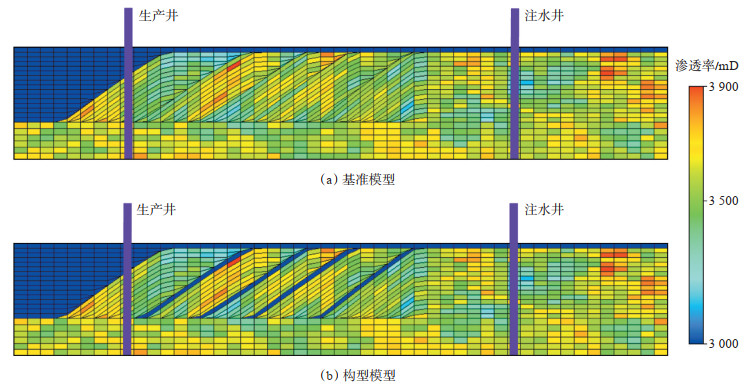
|
下载eps/tif图 图 1 曲流河点坝模型 Fig. 1 Reservoir architecture model of meandering river |
利用Eclipse数值模拟软件,将曲流河点坝构型模型中油井日产液的生产状况Q受构型影响与基准模型中油井日产液的生产状况Q基准代入式(1),计算不同储层构型模式下的控制系数。以此研究曲流河点坝内部侧积层的厚度、孔隙度、渗透率、水平宽度、分布频率及地层倾角对流体运动的控制作用。
(1)侧积层厚度
渤海L油田南区明化镇组下段Ⅰ油组点坝砂体的平均厚度为8 m,其内部侧积层的厚度一般为0.2~2.0m。因此,分别设计3种不同厚度的侧积层(表 2),通过油藏数值模拟可知,F1,F2,F3这3种方案与基准模型方案F0相比,油井的产液能力随着侧积层厚度的增大而降低。
|
|
下载CSV 表 2 不同方案的侧积层设计参数 Table 2 Design parameters of lateral layer for different programs |
根据式(1)选取油井后6个月的日产液数据(投产前期油井生产不稳定),计算曲流河储层构型模式中不同厚度侧积层在不同时间点对流体运动的控制系数(表 3)。从表 3可知,随着隔夹层厚度的增加,控制系数逐渐降低,则曲流河点坝内部侧积层对流体运动的控制作用随着侧积层厚度的增加而增强。
|
|
下载CSV 表 3 不同方案的控制系数统计(2017年) Table 3 Control coefficient of different programs |
由于基准模型的方案F0不存在侧积层,则侧积层厚度为0 m,其对流体运动的控制系数为1。将F0,F1,F2,F3这4种方案的控制系数与侧积层厚度作交会图(图 2)。通过趋势线得到了侧积层厚度与控制系数的关系式为
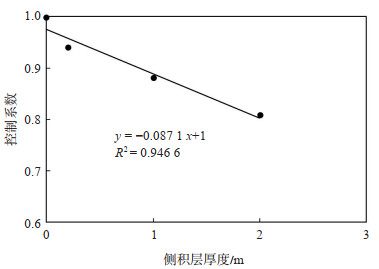
|
下载eps/tif图 图 2 侧积层厚度与控制系数交会图 Fig. 2 Crossplot of lateral layer thickness and control coefficient |
| $ {\alpha _{\text{h}}} = - 0.0871H + 1 $ | (5) |
式中:αh为隔夹层厚度对流体运动的控制系数;H为侧积层厚度,m。
从图 2可看出,控制系数与侧积层厚度存在良好的相关性。同理,应用上述方法分别研究侧积层的孔隙度、渗透率、水平宽度、分布频率及地层倾角等参数对流体运动的控制作用,结果表明:①侧积层厚度对流体运动的控制系数αH随着侧积层厚度H的增加而降低,对流体运动的控制作用随着侧积层厚度的增加而增强,αH = - 0.087 1H + 1;②侧积层孔隙度对流体运动的控制系数αϕ不随侧积层孔隙度ϕ的增加而改变,αϕ = 0.903 4;③侧积层渗透率对流体运动的控制系数αK随着侧积层渗透率K的增加而增加,对流体运动的控制作用随着侧积层渗透率的增加而减弱,
对侧积层渗透率对流体运动的控制系数αK进行转换,转换后
| $ {R_{\text{c}}} = \left[ {\ln \left( {\frac{1}{K}} \right) + 5.16} \right]HRF(\sin \theta + 0.2329) $ | (6) |
式中:Rc为曲流河储层构型模式下侧积层阻力系数;R为侧积层水平宽度,m;F为侧积层分布频率,个;θ为地层倾角,(°)。
渤海L油田南区明化镇组下段Ⅰ油组地层倾角为2°。根据该区点坝精细解剖的研究成果,设计侧积层的渗透率、厚度、水平宽度、分布频率等参数的选取范围,并将设计方案中的各项参数代入式(6),计算侧积层的阻力系数Rc(表 4),作侧积层控制系数与侧积层阻力系数的交会图(图 3)。
|
|
下载CSV 表 4 各方案阻力系数统计 Table 4 Resistance parameters of different programs |
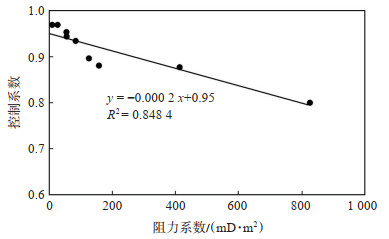
|
下载eps/tif图 图 3 侧积层控制系数与阻力系数交会图 Fig. 3 Crossplot of lateral layer resistance parameter and control coefficient |
通过趋势线得到侧积层控制系数与侧积层阻力系数之间的关系式为
| $ y = - 0.0002x + 0.95 $ | (7) |
从图 3可以看出,侧积层控制系数与侧积层阻力系数之间存在较好的相关性。由此,曲流河储层构型对流体运动的控制系数α的表达式为
| $ \begin{array}{*{20}{c}} {\alpha = - 0.0002\left[ {\ln \left( {\frac{1}{K}} \right) + 5.16} \right]HRF \cdot }\\ {(\sin \theta + 0.2329) + 0.95} \end{array} $ | (8) |
渤海L油田南区明化镇组下段Ⅰ油组储层受曲流河沉积影响,平面上各方向渗透能力差异较大,平面矛盾突出,直接影响注采井网的开发效果。为了降低曲流河储层构型模式带来的渗透能力差异,结合储层构型模式对流体运动的控制系数α,对注采井网的水驱开发效果进行精细研究,确保注入水在储层内部实现均衡驱替。
渤海L油田南区2013年经历大规模综合调整,调整后井网由原来的反九点井网调整为五点井网。因此,以五点井网为研究对象,将五点井网划分为4个区域,且每个区域受储层构型影响的控制系数α各不相同(图 4)。
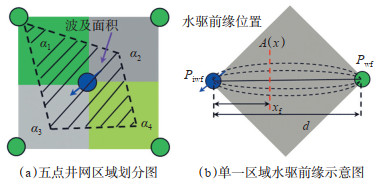
|
下载eps/tif图 图 4 五点井网水驱前缘示意图 Fig. 4 Water drive front of five point well pattern |
假设五点井网单一区域内的渗透率为K,孔隙度为Φ,注采井间的压力差为∆P,水相黏度为μw,油相黏度为μo,目前含水饱和度对应的水相相对渗透率为Krw,目前含水饱和度对应的油相相对渗透率为Kro,注采井之间的距离为d,且水驱前缘前进距离为Xf。据文献[34]报道,根据Buckley-Leverett水驱油理论,考虑储层构型对流体运动的控制作用,则注采井之间的渗流阻力为
| $ R = \frac{1}{\alpha }\int_0^{{X_{\rm{f}}}} {\frac{1}{{\frac{{K{K_{{\rm{ro}}}}\left( {{S_{\rm{w}}}} \right)}}{{{\mu _{\rm{o}}}}} + \frac{{K{K_{rw}}\left( {{S_w}} \right)}}{{{\mu _w}}}}}{\rm{d}}x} + \frac{1}{\alpha }\frac{{{\mu _{\rm{o}}}\left( {d - {X_{\rm{f}}}} \right)}}{{K{K_{{\rm{ro}}}}\left( {{S_{\rm{w}}}} \right)}} $ | (9) |
则流体的流动速度为
| $ {v_{\rm{c}}} = \frac{{\Delta p}}{R} = \frac{{\alpha \Delta p}}{{\int_0^{{x_{\rm{f}}}} {\frac{1}{{\frac{{K{K_{{\rm{ro}}}}\left( {{S_{\rm{w}}}} \right)}}{{{\mu _{\rm{o}}}}} + \frac{{K{K_{{\rm{rw}}}}\left( {{S_{\rm{w}}}} \right)}}{{{\mu _{\rm{w}}}}}}}{\rm{d}}x} + \frac{{{\mu _{\rm{o}}}\left( {d - {X_{\rm{f}}}} \right)}}{{K{K_{{\rm{ro}}}}\left( {{S_{\rm{w}}}} \right)}}}} $ | (10) |
式中:νc为受储层构型影响下的流体运动速度,m/d;Δp为注采压差,MPa。
据文献[35]报道,根据Timur建立的孔隙度与渗透率的关系式为
| $\sqrt K = \frac{{100{\varphi ^{225}}}}{{{S_{\rm{w}}}}} $ | (11) |
式中:ϕ为孔隙度,%;Sw为含水饱和度,%。
假设此时水驱前缘到达的位置为Xf,则有
| $ {X_{\rm{f}}} = \frac{{{{f'}_{\rm{w}}}\left( {{S_{\rm{w}}}} \right)}}{{\phi A}}\int_0^t {{v_{\rm{c}}}{\rm{d}}t} $ | (12) |
式中:fw(Sw)为水驱前缘含水饱和度对应的含水率,%;t为时间,d;A为流动通过的截面面积,m2。
将式(10)-(11)代入式(12)中,令压差调整系数β=Δp调整后/Δp目前,积分整理后,可得单一区域受储层构型影响下的水驱波及系数表达式
| $ {E_{\rm{A}}} = \frac{{{X_{\rm{f}}}}}{d} = \frac{{\frac{{{\mu _{\rm{o}}}}}{{{K_{{\rm{ro}}}}\left( {{S_{\rm{w}}}} \right)}} - \sqrt {\frac{{\mu _{\rm{o}}^2}}{{{K_{{\rm{ro}}}}{{\left( {{S_{\rm{w}}}} \right)}^2}}} - \alpha \beta \left( {\frac{{\mu _{\rm{o}}^2}}{{{K_{{\rm{ro}}}}{{\left( {{S_{\rm{w}}}} \right)}^2}}} - \frac{{\mu _{\rm{w}}^2}}{{{K_{{\rm{rw}}}}{{\left( {{S_{\rm{w}}}} \right)}^2}}}} \right)} }}{{\frac{{{\mu _{\rm{o}}}}}{{{K_{{\rm{r}}0}}\left( {{S_{\rm{w}}}} \right)}} - \frac{{{\mu _{\rm{w}}}}}{{{K_{{\rm{rw}}}}\left( {{S_{\rm{w}}}} \right)}}}} $ | (13) |
式中:β为压差调整系数。
根据式(13)建立波及系数与控制系数的理论图版(图 5)。通过对注采井组的4个调节区域进行单独调整,使各个区域的波及系数达到平衡,从而实现井组注采结构的矢量水驱调整,将井组注采结构调整做到“单井定制”。
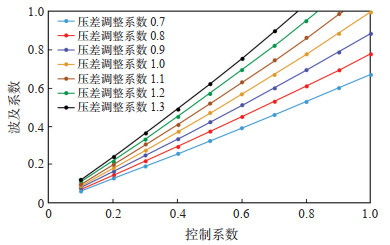
|
下载eps/tif图 图 5 基于储层构型模式的注采结构矢量调整图版 Fig. 5 Vector adjustment chart of injection-production structure based on reservoir architecture model |
在构型精细解剖的基础上,渤海L油田南区明化镇组下段I3砂体各级次构型单元的空间形态、规模、叠置组合关系明确,储层构型模式清晰。因此,选取该区域比较有代表性的D12井组进行注采结构调整先导试验(图 6)。
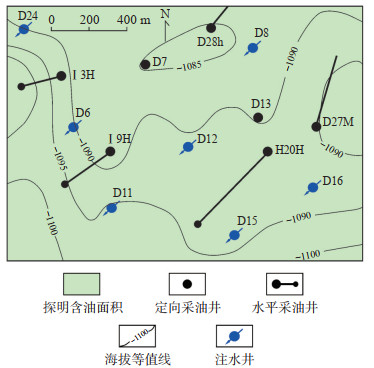
|
下载eps/tif图 图 6 渤海L油田南区D12井组示意图 Fig. 6 D12 well group in southern Bohai L oilfield |
根据地质模式的研究成果,结合高精度地震资料及大量“对子井”、水平井、取心井资料对该区点坝内部构型进行精细解剖,预测了点坝内部侧积体及侧积层的分布状况,并建立了D12井组储层构型分布图(图 7)。
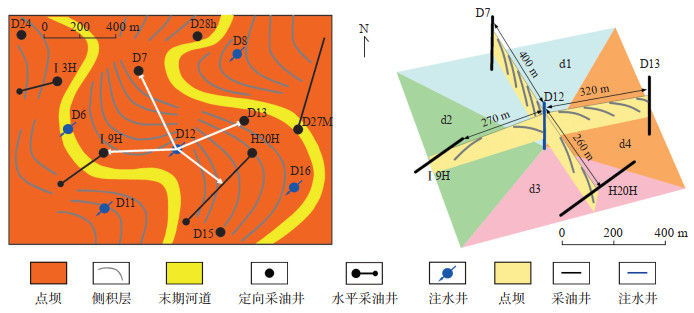
|
下载eps/tif图 图 7 渤海L油田南区D12井组储层构型分布 Fig. 7 Reservoir architecture distribution of D12 well group in southern Bohai L oilfield |
D12井于2016年3月实施转注作业,转注后形成五点井网。以该井组为研究对象,将井网划分为4个区域(图 7)。结合D12井组的储层构型精细解剖,可知每个区域的储层构型模式各不相同。参考渤海L油田南区点坝精细解剖的研究成果,并结合该区域周边井实测数据,应用式(8)分别计算每个区域受储层构型影响的控制系数α。根据计算的储层构型控制系数,参考理论图版(参见图 5)得到各个区域储层构型控制系数对应的波及系数(表 5)。
|
|
下载CSV 表 5 D12井组分区域控制系数 Table 5 Control coefficient of different districts in D12 well group |
D12井组d2区域与d3区域的储层构型控制系数在0.8左右,根据理论图版对应的波及系数也在0.8左右(表 5)。为了使d2区域与d3区域的及系数达到最大化,参考注采矢量调整图版,须将压差提高1.3倍。为此,将I09H的生产压差由原来的1.5 MPa提高1.3倍,增加该井的生产能力。调整后I09H井的生产压差为1.95 MPa,日产油由45 m3/d提高至107 m3/d,综合含水率下降了5%(图 8)。同样,将H20H的生产压差由原来的1.0 MPa调整至1.5 MPa,调整后油井日产油增加了13 m3/d。
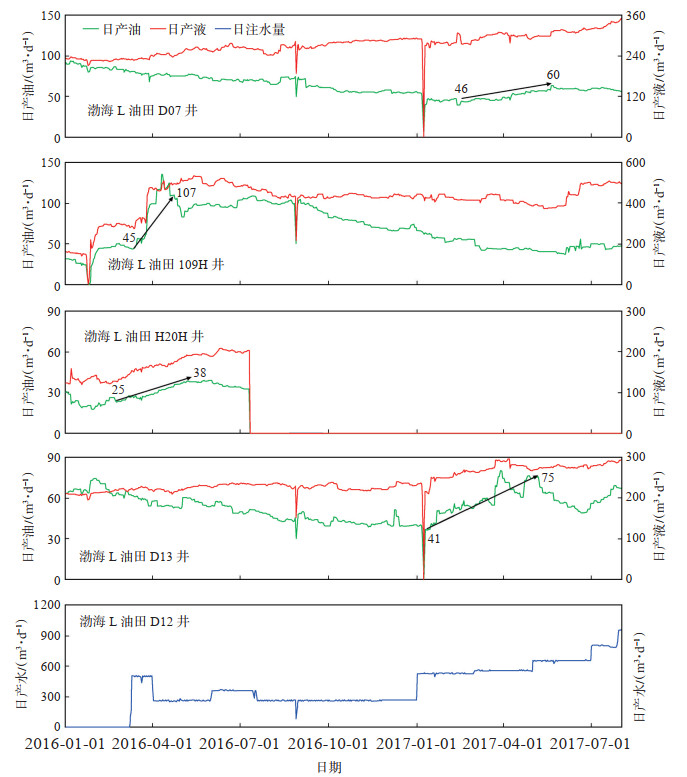
|
下载eps/tif图 图 8 渤海L油田南区D12井组生产动态曲线 Fig. 8 Dynamic curves of D12 well group in southern Bohai L oilfield |
D12井组d1区域与d4区域的储层控制系数在0.6左右,说明该区域受储层构型影响较大。为了使D12井组4个区域的波及系数达到均衡,根据式(13)须要将d1区域与d4区域的压差提高1.7倍。由于d2区域与d3区域的波及系数已经最大化,因此,扩大D12井注入量即可增加d1区域与d4区域的波及系数,使D12井组4个区域波及系数均衡,达到矢量水驱的效果。2017年1月,对D12井的注入量进行调整,由原来的250 m3/d提高至600 m3/d,扩大了d1区域与d4区域的注采压差,实现了D12井组4个区域波及系数最大化。调整后D07井的日产油由原来的46 m3/d提高至60 m3/d,D13井的日产油由原来的41 m3/d提高至75 m3/d(图 8)。通过对注采结构进行矢量调整,D12井组日产油累计增加了123 m3/d,效果显著,不仅有效减缓了产量递减,也为后续提液奠定了能量基础。
该研究成果在构型精细解剖的基础上,通过对井组注采结构进行调整,使注入水达到均衡驱替,具有较高的适用性,有效指导了渤海L油田南区综合调整方案的实施,显著增加了油井提液及注水方案的实施效果,实现了对该区域剩余油的精细挖潜。
5 结论(1)储层构型模式对流体运动的控制作用主要体现在对地层渗透能力的影响上,不同的储层构型模式具有不同的影响效果。
(2)曲流河点坝中的侧积层对流体运动的控制作用不随侧积层的孔隙度增加而改变;侧积层的控制作用随着侧积层渗透率的增加而减弱;侧积层的厚度、水平宽度、分布频率及地层倾角的增加均会使侧积层的控制作用增强。
(3)确定了曲流河储层构型模式对流体运动的控制系数,首次实现了储层构型对流体运动控制作用的定量表征。
(4)推导了曲流河储层构型影响下的水驱波及系数表达式,建立了基于曲流河储层构型的注采结构矢量调整图版,并在渤海L油田南区取得了很好的调整效果,实现了对该区域剩余油的精细挖潜。
| [1] |
束青林. 河道砂侧积体对剩余油分布的影响:以孤岛油田馆上段3~4砂组高弯度曲流河为例. 油气地质与采收率, 2005, 12(2): 45-48. SHU Q L. Effect of lateral accretion sandbodies of channel sands on the distribution of remaining oil:Taking high-sinuosity meandering river of 3~4 sand groups in Upper Ng of Gudao oilfield as example. Petroleum Geology and Recovery Efficiency, 2005, 12(2): 45-48. DOI:10.3969/j.issn.1009-9603.2005.02.014 |
| [2] |
王鸣川, 朱维耀, 董卫宏, 等. 曲流河点坝型厚油层内部构型及其对剩余油分布的影响. 油气地质与采收率, 2013, 20(3): 14-17. WANG M C, ZHU W Y, DONG W H, et al. Study on distribution and influence factors of remaining oil in point bar of meandering river. Petroleum Geology and Recovery Efficiency, 2013, 20(3): 14-17. DOI:10.3969/j.issn.1009-9603.2013.03.004 |
| [3] |
赵伦, 梁宏伟, 张祥忠, 等. 砂体构型特征与剩余油分布模式:以哈萨克斯坦南图尔盖盆地Kumkol South油田为例. 石油勘探与开发, 2016, 43(3): 433-441. ZHAO L, LIANG H W, ZHANG X Z, et al. Relationship between sandstone architecture and remaining oil distribution pattern:a case of the Kumkol South oilfield in South Turgay Basin, Kazakstan. Petroleum Exploration and Development, 2016, 43(3): 433-441. |
| [4] |
陈程, 宋新民, 李军. 曲流河点砂坝储层水流优势通道及其对剩余油分布的控制. 石油学报, 2012, 33(2): 257-263. CHEN C, SONG X M, LI J. Dominant flow channels of pointbar reservoirs and their control on the distribution of remaining oils. Acta Petrolei Sinica, 2012, 33(2): 257-263. |
| [5] |
MIALL A D. Architectural-elements analysis:a new method of facies analysis applied to fluvial deposits. Earth Science Reviews, 1985, 22(4): 261-308. DOI:10.1016/0012-8252(85)90001-7 |
| [6] |
MIALL A D. Reservoir heterogeneities in fluvial sandstones:Lessons from outcrop studies. AAPG Bulletin, 1988, 72(6): 682697. |
| [7] |
ALLEN J R L. Studies in fluviatile sedimentation:bars, bar complexes and sandstone sheets(lower-sinuosity braided streams) in the brownstones(L. Devonian), Welsh Borders. Sedimentary Geology, 1983, 33(4): 237-293. DOI:10.1016/0037-0738(83)90076-3 |
| [8] |
MIALL A D. The geology of fluvial deposits. Berlin Heidelberg: Springer, 1996.
|
| [9] |
MARTIN A J, SOLOMONS T, HATTMANN D J. Characterization of petrophysical flow units in carbonate reservoirs. AAPG Bulletin, 1997, 81(5): 731-759. |
| [10] |
李顺明, 宋新民, 蒋有伟, 等. 高尚堡油田砂质辫状河储集层构型与剩余油分布. 石油勘探与开发, 2011, 38(4): 474-482. LI S M, SONG X M, JIANG Y W, et al. Architecture and remaining oil distribution of the sandy braided river reservoir in the Gaoshangpu Oilfield. Petroleum Exploration and Development, 2011, 38(4): 474-482. |
| [11] |
周新茂, 高兴军, 田昌炳, 等. 曲流河点坝内部构型要素的定量描述及应用. 天然气地球科学, 2010, 21(3): 421-426. ZHOU X M, GAO X J, TIAN C B, et al. Quantitative description of internal architecture in point bar of meandering river. Natural Gas Geoscience, 2010, 21(3): 421-426. |
| [12] |
岳大力, 吴胜和, 谭河清, 等. 曲流河古河道储层构型精细剖:以孤东油田七区西馆陶组为例. 地学前缘, 2008, 15(1): 101109. YUE D L, WU S H, TAN H Q, et al. An anatomy of paleo channel reservoir architecture of meandering river reservoir:a case study of Guantao Formation, the west 7th block of Gudong Oilfield. Earth Science Frontiers, 2008, 15(1): 101-109. DOI:10.3321/j.issn:1005-2321.2008.01.012 |
| [13] |
邹志文, 斯春松, 杨梦云. 隔夹层成因、分布及其对油水分布的影响:以准噶尔盆地腹部莫索湾莫北地区为例. 岩性油气藏, 2010, 22(3): 66-70. ZHOU Z W, SI C S, YANG M Y. Origin and distribution of interbeds and the influence on oil-water layer:an example from Mosuowan area in the hinterland of Junggar Basin. Lithologic Reservoirs, 2010, 22(3): 66-70. DOI:10.3969/j.issn.1673-8926.2010.03.013 |
| [14] |
甘立琴, 苏进昌, 谢岳, 等. 曲流河储层隔夹层研究:以秦皇岛32-6油田为例. 岩性油气藏, 2017, 29(6): 128-134. GAN L Q, SU J C, XIE Y, et al. Interlayers of meandering river reservoir:a case from Qinhuangdao 32-6 oilfield. Lithologic Reservoirs, 2017, 29(6): 128-134. DOI:10.3969/j.issn.1673-8926.2017.06.016 |
| [15] |
胡浩. 基于砂体结构的剩余油挖潜调整措施研究. 岩性油气藏, 2016, 28(4): 113-120. HU H. Adjustment measures of remaining oil tapping based on sand body structure. Lithologic Reservoirs, 2016, 28(4): 113120. |
| [16] |
胡丹丹, 唐玮, 常毓文, 等. 厚油层层内夹层对剩余油的影响研究. 特种油气藏, 2009, 16(3): 49-52. HU D D, TANG W, CHANG Y W, et al. Study on the influence of intercalation on remaining oil distribution in thick reservoirs. Special Oil and Gas Reservoirs, 2009, 16(3): 49-52. DOI:10.3969/j.issn.1006-6535.2009.03.014 |
| [17] |
刘超, 李云鹏, 张伟, 等. 渤海海域A油田夹层控制下的剩余油分布模式. 岩性油气藏, 2017, 29(5): 148-154. LIU C, LI Y P, ZHANG W, et al. Remaining oil distribution pattern controlled by interlayer in A oilfield in Bohai Sea. Lithologic Reservoirs, 2017, 29(5): 148-154. DOI:10.3969/j.issn.1673-8926.2017.05.018 |
| [18] |
张建兴, 林承焰, 张宪国, 等. 基于储层构型与油藏数值模拟的点坝储层剩余油分布研究. 岩性油气藏, 2017, 29(4): 146-153. ZHANG J X, LIN C Y, ZHANG X G, et al. Remaining oil distribution of point bar reservoir based on reservoir architecture and reservoir numerical simulation. Lithologic Reservoirs, 2017, 29(4): 146-153. DOI:10.3969/j.issn.1673-8926.2017.04.018 |
| [19] |
黄辉, 范玉平, 孙立旭. "动静结合法"在剩余油定量分布中的应用研究. 石油钻采工艺, 2006, 28(6): 35-38. HUANG H, FAN Y P, SUN L X. Study on residual oil quantitative distribution in abnormal high pressure reservoir by static and dynamic methods. Oil Drilling & Production Technology, 2006, 28(6): 35-38. DOI:10.3969/j.issn.1000-7393.2006.06.011 |
| [20] |
尹太举, 张昌民, 赵红静. 地质综合法预测剩余油. 地球科学进展, 2006, 21(5): 539-544. YIN T J, ZHANG C M, ZHAO H J. Remaining oil prediction based on comprehensive geological analysis methods. Advances in Earth Science, 2006, 21(5): 539-544. DOI:10.3321/j.issn:1001-8166.2006.05.013 |
| [21] |
李阳, 王端平, 刘建民. 陆相水驱油藏剩余油富集区研究. 石油勘探与开发, 2005, 32(3): 91-96. LI Y, WANG D P, LIU J M. Remaining oil enrichment areas in continental water flooding reservoirs. Petroleum Exploration and Development, 2005, 32(3): 91-96. DOI:10.3321/j.issn:1000-0747.2005.03.023 |
| [22] |
姜汉桥, 谷建伟, 陈月明, 等. 剩余油分布规律的精细数值模拟. 石油大学学报(自然科学版), 1999, 23(5): 31-34. JIANG H Q, GU J W, CHEN Y M, et al. Fine simulation for distribution of remaining oil in reservoir. Journal of The University of Petroleum, China(Edition of Natural Science), 1999, 23(5): 31-34. DOI:10.3321/j.issn:1000-5870.1999.05.009 |
| [23] |
赵春明, 胡景双, 霍春亮, 等. 曲流河与辫状河沉积砂体连通模式及开发特征:以渤海地区秦皇岛32-6油田为例. 油气地质与采收率, 2009, 16(6): 88-91. ZHAO C M, HU J S, HUO C L, et al. Sandbody interconnectivity architecture and development characteristics of meandering river and braided river deposits:a case study of Qinhuangdao 32-6 Oilfield, Bohai area. Petroleum Geology and Recovery Efficiency, 2009, 16(6): 88-91. DOI:10.3969/j.issn.1009-9603.2009.06.024 |
| [24] |
刘超, 赵春明, 廖新武, 等. 海上油田大井距条件下曲流河储层内部构型精细解剖及应用分析. 中国海上油气, 2014, 26(1): 58-64. LIU C, ZHAO C M, LIAO X W, et al. A refined anatomy of the internal structure of meandering river reservoirs under large well spacing in offshore oilfields and its application. China Offshore Oil and Gas, 2014, 26(1): 58-64. |
| [25] |
CAYO P, ARTHUR V V. Meandering stream deposits from the Tertiary of the southern Pyrenees//MIALL A D. Fluvial sedimentology. Alberta: McAra Printing Limited, 1978: 469-485.
|
| [26] |
薛培华. 河流点坝相储层模式概论, 1991, 23-35. XUE P H. The introduction of reservoir model for point bar facies, 1991, 23-35. |
| [27] |
赵翰卿. 河道砂岩中夹层的稳定性. 大庆石油地质与开发, 1985, 4(3): 1-11. ZHAO H Q. Continuity of intercalated beds in channel sandstones. Petroleum Geology & Oilfield Development in Daqing, 1985, 4(3): 1-11. |
| [28] |
金强, BROWTON J R. 用生产井信息确定储层非均质性. 石油大学学报(自然科学版), 1999, 23(2): 18-21. JIN Q, BROWTON J R. Estimation of reservoir heterogeneity with production data. Journal of The University of Petroleum, China(Edition of Natural Science), 1999, 23(2): 18-21. DOI:10.3321/j.issn:1000-5870.1999.02.005 |
| [29] |
杨少春. 储层非均质性定量研究的新方法. 石油大学学报(自然科学版), 2000, 24(1): 53-56. YANG S C. A new method for quantitatively studying reservoir heterogeneity. Journal of The University of Petroleum, China (Edition of Natural Science), 2000, 24(1): 53-56. |
| [30] |
龙明, 徐怀民, 江同文, 等. 滨岸相碎屑岩储集层构型动态评价. 石油勘探与开发, 2012, 39(6): 754-763. LONG M, XU H M, JIANG T W, et al. Performance evaluation for littoral-facies clastic reservoir architecture. Petroleum Exploration and Development, 2012, 39(6): 754-763. |
| [31] |
岳大力, 林承焰, 吴胜和, 等. 储层非均质定量表征方法在礁灰岩油田开发中的应用. 石油学报, 2004, 25(5): 75-79. YUE D L, LIN C Y, WU S H, et al. Application of quantitative method for characterizing reservoir heterogeneity to the development of reef limestone reservoir. Acta Petrolei Sinica, 2004, 25(5): 75-79. DOI:10.3321/j.issn:0253-2697.2004.05.015 |
| [32] |
尹太举, 张昌民, 樊中海, 等. 地下储层建筑结构预测模型的建立. 西安石油学院学报(自然科学版), 2002, 17(3): 7-11. YIN T J, ZHANG C M, FAN Z H, et al. Establishment of the prediction models of reservoir architectural elements. Journal of Xi'an Petroleum Institute(Natural Science Edition), 2002, 17(3): 7-11. DOI:10.3969/j.issn.1673-064X.2002.03.002 |
| [33] |
LEEDER M R. Fluviatile fining-upwards cycles and the magnitude of paleochannels. Geological Magazine, 1973, 110(3): 265276. DOI:10.1017/S0016756800036098 |
| [34] |
洪世铎. 油藏物理基础. 北京: 石油工业出版社, 1985. HONG S D. Reservoir physical basis. Beijing: Petroleum Industry Press, 1985. |
| [35] |
张冲, 张占松, 张超谟. 基于等效岩石组分理论的渗透率解释模型. 测井技术, 2014, 38(6): 690-694. ZHANG C, ZHANG Z S, ZHANG C M. A permeability interpretation model based on equivalent rock elements theory. Well Logging Technology, 2014, 38(6): 690-694. DOI:10.3969/j.issn.1004-1338.2014.06.010 |
 2019, Vol. 31
2019, Vol. 31



