随着能源需求的不断增大和压裂改造技术的长足进步，致密油作为一种储量丰富的非常规油气[中国致密油资源总量为(106.7~111.5)亿t]，是目前我国较为现实的石油接替资源^[1-3]。致密油藏由于低孔低渗，其开发实践表明，常规压裂改造很难满足工业生产需要^[4-6]，目前通常采用水平井钻井结合分段多簇射孔压裂的方式形成多条高导流能力裂缝，并利用缝间干扰产生复杂裂缝网络，其大小用储层改造体积(SRV)表示，改善近井地带储层的渗透性，增大泄流面积，从而提高单井产能^[7-9]。

国内外众多学者为了研究考虑SRV的压裂水平井生产动态，主要应用数值模拟方法和解析/半解析方法。数值模拟方法^[10-12]可灵活处理复杂裂缝形态，但很难考虑非常规储层的渗流机理，而解析/半解析方法因其严格的数学推导和较高的计算效率成为目前的研究热点，其中Brown等^[13]提出的三线性流模型和Stalgorova等^[14]提出的五线性流模型因其简单有效的特点而被众多学者采用。姚军等^[15]针对低渗油藏非达西渗流特征，在三线性流模型中引入了启动压力梯度，分析了低渗透油藏压裂水平井压力动态特征。苏玉亮等^[16]利用三线性流模型研究了致密油藏水平井多级压裂布缝策略，分析了SRV与累积产油量的关系。赵二猛等^[17]基于双重介质模型，建立了窜流系数随着距主裂缝距离逐渐变化的致密油体积压裂水平井线性流模型。苏玉亮等^[18]、姬靖皓等^[19]、JI等^[20]结合致密储层低速非达西流动和裂缝应力敏感特征建立了致密油藏体积压裂水平井五区复合流动模型，分析了其相应的压力动态和产能变化特征。为了考虑段间和簇内渗流规律的差异性，郭肖等^[21]建立了页岩气藏分段多簇压裂水平井复合线性流模型，然而，目前还没有适合致密油藏分段多簇压裂水平井的产能模型。因此，基于前人研究成果，结合致密储层低速非达西流动、裂缝应力敏感特征，并考虑段间渗流场和簇间渗流场差异性，建立致密油藏分段多簇压裂水平井非稳态产能模型，以期为致密油藏分段多簇压裂水平井产能评价和裂缝参数优化提供理论依据。

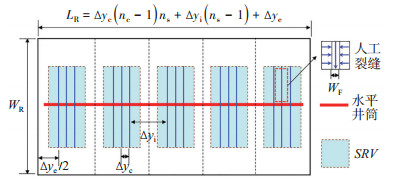
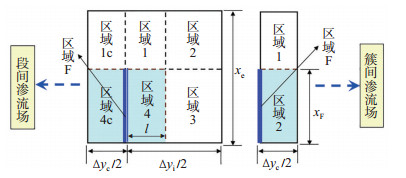
致密油藏经水平井分段多簇压裂改造后，每个压裂段内会形成多簇高导流能力裂缝，簇间裂缝由于缝间干扰形成复杂裂缝网络，经过简化的物理模型如图 1所示。图 1中：由于分段多簇压裂形成的裂缝区别于多段单簇压裂缝，段间渗流场改造程度弱，簇间渗流场改造程度强，储层渗透性得到改善，2个渗流场具有明显的差异性，不能简单地应用三线性流模型或五线性流模型来进行表征。如图 2所示，段间渗流场为每段改造体间的渗流区域，可划分为7个区域：区域1、区域1 c、区域2为未改造区，可采用单重介质模型并引入启动压力梯度来表征其低速非达西流动特征；区域3为部分受效区(改造程度弱)，区域4、区域4 c为有效改造区(改造程度强)，这3个区域可利用双重介质模型来进行表征，并考虑裂缝渗透率应力敏感性；区域F为压裂裂缝区，考虑裂缝渗透率应力敏感性。簇间渗流场为每段改造体内部的渗流区域，可划分为3个区域：区域1为未改造区；区域2为有效改造区；区域F为人工裂缝区。簇间渗流场各区域表征方法同段间渗流场。图 1和图 2中：L_R为油藏长度，m；W_R (2 x_e)为油藏宽度，m；n_s为压裂段数；n_c为每段压裂簇数；Δy_c为簇间距，m；Δy_i为段间距，m；Δy_e为两端裂缝到储层边界的距离之和，m；l为段裂缝间改造体积的延伸长度，m；x_F为裂缝半长，m；w_F为裂缝宽度，m。

图 1

Fig. 1

下载eps/tif图 图 1 分段多簇压裂裂缝与改造体积示意图 Fig. 1 Schematic diagram of segmented multi-cluster fractures and SRV

图 2

Fig. 2

下载eps/tif图 图 2 段间渗流场和簇间渗流场示意图 Fig. 2 Seepage field schematic diagram of segments and clusters

物理模型的其他假设条件为：①油藏外边界封闭，压裂水平井位于油藏中心以定井底流压生产；②各裂缝性质相同且每条裂缝都完全穿透储层；③单相微可压缩液体等温渗流，忽略重力、毛管压力和井筒中的流动阻力；④流体流动为线性流动，由未改造区流向改造区进而从压裂裂缝流入水平井筒。

首先定义相关无因次变量如表 1所列，P_i为原始地层压力，MPa；P_wf为井底流压，MPa；η_ref为参考导压系数，μm²(/ mPa·s·MPa^-1)；q_F为单条裂缝产量，m³/d；t为时间，d；μ为流体黏度，mPa·s；B为原油体积系数；K_ref为参考渗透率，D；h为储层厚度，m；α为形状因子；K_m为基质渗透率，D；K_fi为原始状态下的裂缝渗透率，D；L_ref为参考长度，m；Ф为孔隙度，%；C_t为综合压缩系数，MPa^-1；K_Fi为原始状态下的人工裂缝渗透率，D；C_L为流体压缩系数，MPa^-1；λ_m为启动压力梯度，MPa/ m；γ为渗透率模量，MPa^-1。其中的下标，j代表各个渗流区域；i代表原始状态；m，f代表双重介质的基质和裂缝系统；F代表人工压裂裂缝；ref代表参考值；D代表无因次。

表 1(Table 1)

表 1 无因次变量的定义 Table 1 Dimensionless variables 无因次压力 无因次时间 无因次产量 无因次导压系数 窜流系数 弹性储容比 无因次导流能力 无因次启动压力梯度 无因次启动压力程度 无因次渗透率模量 无因次距离 $ P_{\mathrm{jD}}=\frac{P_{\mathrm{i}}-P_{\mathrm{j}}}{P_{\mathrm{i}}-P_{\mathrm{wf}}}, \mathrm{j}=1, 2, 3, 4, 1 \mathrm{c}, 4 \mathrm{c}, \mathrm{F}$ $t_{\mathrm{D}}=\frac{3.6 \eta_{\mathrm{ref}}}{L_{\mathrm{ref}}^{2}} t $ $q_{\mathrm{FD}}\left(t_{\mathrm{D}}\right)=\frac{1.842 \times 10^{-3} q_{\mathrm{F}}(t) \mu B}{K_{\mathrm{ref}} h\left(P_{\mathrm{i}}-P_{\mathrm{wf}}\right)} $ $\eta_{\mathrm{jD}}=\frac{\eta_{\mathrm{j}}}{\eta_{\mathrm{ref}}}, \mathrm{j}=1, 2, 3, 4, 1 \mathrm{c}, 4 \mathrm{c}, \mathrm{F} $ $ \lambda=\alpha \frac{K_{\mathrm{m}}}{K_{\mathrm{fi}}} L_{\mathrm{ref}}^{2}$ $\omega = \frac{{{{\left( {\mathit{\Phi }{C_{\rm{t}}}} \right)}_{\rm{f}}}}}{{{{\left( {\mathit{\Phi }{C_{\rm{t}}}} \right)}_{\rm{f}}} + {{\left( {\mathit{\Phi }{C_{\rm{t}}}} \right)}_{\rm{m}}}}} $ $ C_{\mathrm{FD}}=\frac{K_{\mathrm{Ki}} w_{\mathrm{F}}}{K_{\mathrm{ref}} L_{\mathrm{ref}}}$ $ \lambda_{\mathrm{D}}=C_{\mathrm{L}} \lambda_{\mathrm{m}} L_{\mathrm{ref}}$ $G=\frac{\lambda_{\mathrm{m}} L_{\mathrm{ref}}}{P_{\mathrm{i}}-P_{\mathrm{wf}}} $ $ \gamma_{\mathrm{D}}=\left(P_{\mathrm{i}}-P_{\mathrm{wf}}\right) \gamma$ $x_{\mathrm{D}}=\frac{x}{L_{\mathrm{ref}}}, y_{\mathrm{D}}=\frac{y}{L_{\mathrm{ref}}} $

下载CSV 表 1 无因次变量的定义 Table 1 Dimensionless variables

对于簇间渗流场，选取1/4裂缝控制区域进行研究时可利用三线性流模型进行表征，此时区域F的无因次化渗流数学模型可表示为

为了消除式(1)的非线性，可采用Pedrosa ^[22]变换式如下：

将式(2)带入式(1)，并对式(1)进行Pedrosa ^[22]变换。通常γ_D非常小，因此零阶摄动即可满足计算精度的要求。对变换后的式子取零阶摄动，而后进行Laplace变换(t → u)得到

据姚军等^[15]的求解过程，可求得本文模型单条簇裂缝在拉氏空间的产量解为

其中，$ \beta_{\mathrm{F}}=\frac{2 K_{1} \beta_{2}}{K_{\mathrm{Fi}} w_{\mathrm{D}} x_{\mathrm{FD}} \alpha_{1}} \frac{G}{u}, \alpha_{2}=\frac{2 K_{2 \mathrm{fi}}}{K_{\mathrm{Fi}} w_{\mathrm{D}}} \beta_{2}+\frac{u}{\eta_{\mathrm{FD}}}, $${\beta _2} = \sqrt {{\alpha _1}} \tanh \left[ {\frac{{\sqrt {{\alpha _1}} \left( {{y_{{\rm{cD}}}} - {w_{\rm{D}}}} \right)}}{2}} \right], {\alpha _1} = \frac{{{K_1}}}{{{K_{2{\rm{fi}}}}{x_{{\rm{FD}}}}}}{\beta _1} + {f_2}(u), $$ {\beta _1} = \frac{{{r_2}{{\rm{e}}^{{r_1}\left( {{x_{{\rm{FD}}}} - {x_{{\rm{eD}}}}} \right)}} - {r_1}{{\rm{e}}^{{r_2}\left( {{x_{{\rm{FD}}}} - {x_{{\rm{eD}}}}} \right)}}}}{{\left( { - \frac{{{r_2}}}{{{r_1}}}} \right){{\rm{e}}^{{r_1}\left( {{x_{{\rm{FD}}}} - {x_{{\rm{eD}}}}} \right)}} + {{\rm{e}}^{{r_2}\left( {{x_{{\rm{FD}}}} - {x_{{\rm{eD}}}}} \right)}}}}, $$f_{2}(u)=\frac{\omega_{2} u}{\eta_{2 \mathrm{D}}}+\frac{\lambda_{2}\left(1-\omega_{2}\right) u}{\lambda_{2} \eta_{2 \mathrm{D}}+\left(1-\omega_{2}\right) u}, $$ {r_1} = \frac{{{\lambda _{\rm{D}}} + \sqrt {\frac{{4u}}{{{\eta _{{\rm{1D}}}}}} + \lambda _{\rm{D}}^2} }}{2}, {r_2} = \frac{{{\lambda _{\rm{D}}} - \sqrt {\frac{{4u}}{{{\eta _{{\rm{1D}}}}}} + \lambda _{\rm{D}}^2} }}{2}$。

对于段间渗流场，选取1/2裂缝控制区域进行研究，区域F在拉氏空间中的无因次化渗流数学模型可表示为

段间渗流场的左半边类似于一个三线性流模型，因此据姚军等^[15]的求解过程，区域4 c的解可表示为

由物理模型假设可知，段间渗流场的区域4 c与簇间渗流场的区域2都属于有效改造区，因此，式(6)中的β_4c和K_4fi等于式(4)中的β₂和K_2fi。段间渗流场的右半边类似于一个五线性流模型，根据姬靖皓等^[19]、JI等^[20]的研究，区域4的解可表示为

其中，${\beta _4} = \frac{{ - {\alpha _0}\sqrt {{\alpha _1}} \cosh \left[ {\sqrt {{\alpha _1}} \left( {\frac{{{w_{\rm{D}}}}}{2} - {l_{\rm{D}}}} \right)} \right] - \sqrt {{\alpha _1}} \sinh \left[ {\sqrt {{\alpha _1}} \left( {\frac{{{w_{\rm{D}}}}}{2} - {l_{\rm{D}}}} \right)} \right]}}{{{\alpha _0}\sinh \left[ {\sqrt {{\alpha _1}} \left( {\frac{{{w_{\rm{D}}}}}{2} - {l_{\rm{D}}}} \right)} \right] + \cosh \left[ {\sqrt {{\alpha _1}} \left( {\frac{{{w_{\rm{D}}}}}{2} - {l_{\rm{D}}}} \right)} \right]}}, $$ {\alpha _1} = \frac{{{K_1}}}{{{K_{4{\rm{fi}}}}{x_{{\rm{FD}}}}}}{\beta _1} + {f_4}(u), {\alpha _0} = - \frac{{\sqrt {{\alpha _2}} }}{{{M_{34}}\sqrt {{\alpha _1}} }} \cdot $$\tanh \left[\sqrt{\alpha_{2}}\left(\frac{y_{i \mathrm{D}}}{2}-l_{\mathrm{D}}\right)\right], $$ {\beta _1} = \frac{{{r_2}{{\rm{e}}^{{r_1}\left( {{x_{{\rm{FD}}}} - {x_{{\rm{eD}}}}} \right)}} - {r_2}{{\rm{e}}^{{r_2}\left( {{x_{{\rm{FD}}}} - {x_{{\rm{eD}}}}} \right)}}}}{{\left( { - \frac{{{r_2}}}{{{r_1}}}} \right){{\rm{e}}^{{r_1}\left( {{x_{{\rm{FD}}}} - {x_{{\rm{eD}}}}} \right)}} + {{\rm{e}}^{{r_2}\left( {{x_{{\rm{FD}}}} - {x_{{\rm{eD}}}}} \right)}}}}, $$ f_{4}(u)=\frac{\omega_{4} u}{\eta_{4 \mathrm{D}}}+\frac{\lambda_{4}\left(1-\omega_{4}\right) u}{\lambda_{4} \eta_{4 \mathrm{D}}+\left(1-\omega_{4}\right) u}, $${\alpha _2} = \frac{{{K_2}}}{{{K_{3{\rm{fi}}}}{x_{{\rm{FD}}}}}}{\beta _2} + {f_3}(u), $$ f_{3}(u)=\frac{\omega_{3} u}{\eta_{3 \mathrm{D}}}+\frac{\lambda_{3}\left(1-\omega_{3}\right) u}{\lambda_{3} \eta_{3 \mathrm{D}}+\left(1-\omega_{3}\right) u}, $$ {\beta _2} = \frac{{{m_2}{{\rm{e}}^{{m_1}\left( {{x_{{\rm{FD}}}} - {x_{{\rm{eD}}}}} \right)}} - {m_2}{{\rm{e}}^{{m_2}\left( {{x_{{\rm{FD}}}} - {x_{{\rm{eD}}}}} \right)}}}}{{\left( { - \frac{{{m_2}}}{{{m_1}}}} \right){{\rm{e}}^{{m_1}\left( {{x_{{\rm{FD}}}} - {x_{{\rm{eD}}}}} \right)}} + {{\rm{e}}^{{m_2}\left( {{x_{{\rm{FD}}}} - {x_{{\rm{eD}}}}} \right)}}}}, $$ {r_1} = \frac{{{\lambda _{\rm{D}}} + \sqrt {\frac{{4u}}{{{\eta _{{\rm{1D}}}}}} + \lambda _D^2} }}{2}, $$ {r_2} = \frac{{{\lambda _{\rm{D}}} - \sqrt {\frac{{4u}}{{{\eta _{{\rm{1D}}}}}} + \lambda _D^2} }}{2}, $$m_{1}=\frac{\lambda_{\mathrm{D}}+\sqrt{\frac{4 u}{\eta_{2 \mathrm{D}}}+\lambda_{\mathrm{D}}^{2}}}{2}, $${m_2} = \frac{{{\lambda _{\rm{D}}} - \sqrt {\frac{{4u}}{{{\eta _{2{\rm{D}}}}}} + \lambda _{\rm{D}}^2} }}{2} $。

那么，令${\alpha _{\rm{f}}} = \frac{{{K_{4{\rm{fi}}}}}}{{{K_{F{\rm{i}}}}{w_{\rm{D}}}}}\left( {{\beta _4} + {\beta _{{\rm{4c}}}}} \right) + \frac{u}{{{\eta _{{\rm{5D}}}}}}, $$\beta_{\mathrm{f}}=\frac{K_{1}\left(\beta_{4}+\beta_{4 \mathrm{c}}\right)}{K_{\mathrm{Fi}} w_{\mathrm{D}} x_{\mathrm{FD}} \alpha_{1}} \frac{G}{u}+$$ \frac{K_{4 \mathrm{fi}} C}{K_{\mathrm{Fi}} w_{\mathrm{D}}}\left(\frac{K_{1}}{K_{4 \mathrm{fi}} x_{\mathrm{FD}} \alpha_{1}}-\frac{K_{2}}{K_{3 \mathrm{fi}} x_{\mathrm{FD}} \alpha_{2}}\right) \frac{G}{u}$，则可求得单条段裂缝在拉氏空间中的解为

在得到上述段间渗流场和簇间渗流场的单条裂缝解后，利用Stehfest ^[23]数值反演方法得到其时空间的解，而后采用Meyer等^[24]的方法进行产量叠加处理，分别定义不同位置裂缝所对应的形状因子：端部裂缝形状参数为δ_e = W_R/Δy_e，段间裂缝形状参数为δ_i = W_R/Δy_i，簇间裂缝形状参数为δ_c = W_R/Δy_c。则分段多簇压裂水平井的产量解可表示为

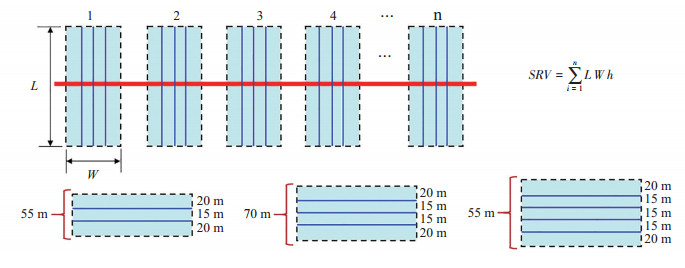
以某致密油藏1口分段多簇压裂水平井基本参数为例，原始地层压力为15 MPa，井底流压为5 MPa，水平井长度为1 400 m，8段2簇压裂(簇间距15 m)，每段改造体两端裂缝各向外延展的改造体宽度为20 m，可根据图 3进行SRV大小的计算。裂缝半长为100 m，裂缝导流能力为5 D·cm，油藏厚度为20 m，基质渗透率为0.1 mD，孔隙度为14%，原油黏度为4 mPa·s，体积系数为1.2，改造区基质和裂缝压缩系数分别为0.000 75 MPa^-1和0.001 MPa^-1，启动压力梯度为0.005 MPa/m，裂缝渗透率模量为0.02 MPa^-1。

图 3

Fig. 3

下载eps/tif图 图 3 改造体积计算方法示意图 Fig. 3 Schematic diagram of calculating SRV

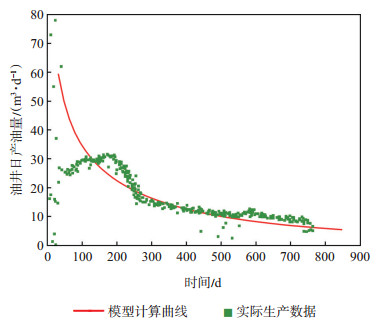
由图 4可以看出，油井生产初期存在压裂液反排现象，产量波动大，中后期模型计算结果与实际生产数据拟合程度较高，进一步证明了本文所推导的非稳态产能模型具有一定的准确性。

图 4

Fig. 4

下载eps/tif图 图 4 计算数据与实际数据对比图 Fig. 4 Comparison of calculated data and actual production data

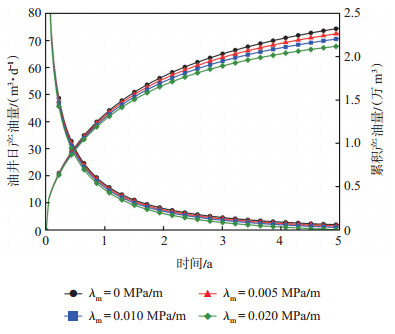
低速非达西流动的程度可利用启动压力梯度值的大小来进行表征^[25-26]，启动压力梯度越大，储层低速非达西流动越明显，其对油井产能动态特征的影响越大。如图 5所示，启动压力梯度主要影响油井中后期的产能，这是因为分段多簇压裂会在近井地带形成复杂裂缝网络，有效提高了储层的渗透性，从而减小了非达西流动对油井前期产能的影响。随启动压力压力梯度的增大，油井中后期的产量越小，累积产油量也越小。

图 5

Fig. 5

下载eps/tif图 图 5 启动压力梯度对油井产能的影响 Fig. 5 Effect of threshold pressure gradient on oil well productivity

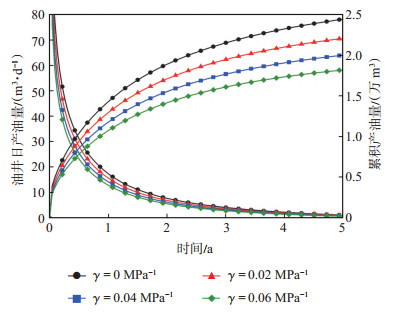
图 6表明了裂缝渗透率应力敏感对致密油藏分段多簇压裂水平井产能动态的影响。由于主裂缝和SRV区域的裂缝是流体主要的渗流通道，裂缝应力敏感性的存在会导致其渗透性随开发过程中地层压力的减小而降低，因此，裂缝的应力敏感性影响油井整个生产阶段。应力敏感系数越大，油井的产油量和累积产油量越低。

图 6

Fig. 6

下载eps/tif图 图 6 裂缝渗透应力敏感性对油井产能的影响 Fig. 6 Effect of fracture stress sensitivity on oil well productivity

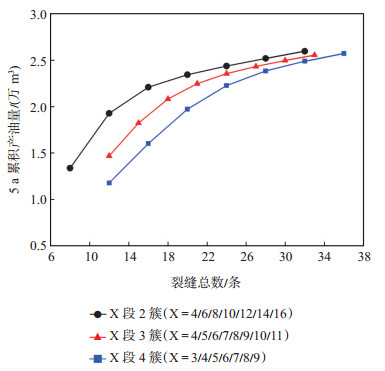
现场分段多簇压裂每段簇数一般为2~4簇。分别计算22种布缝形式下(4/6/8/10/12/14/16段2簇缝共7种；4/5/6/7/8/9/10/11段3簇缝共8种；3/4/5/6/7/8/9段4簇缝共7种)油井生产5 a的累积产油量。从图 7可以看出，相同裂缝分布形式下，裂缝条数的增加可有效提高油井的产能，但累积产油量的增幅会随着裂缝条数的增加增幅逐渐变缓。不同布缝方式对比可以看出，当裂缝总数较少时，裂缝的段簇比对累积产油量影响较大，而当裂缝条数较多时，段簇比对累积产油量影响不明显。相同裂缝条数下，段簇比越大，累积产油量越大，这是因为压裂后油井生产效率很大程度上取决于单条裂缝的储层改造范围，簇数越多，簇间干扰越严重。

图 7

Fig. 7

下载eps/tif图 图 7 裂缝条数对油井产能的影响 Fig. 7 Effect of fracture number on oil well productivity

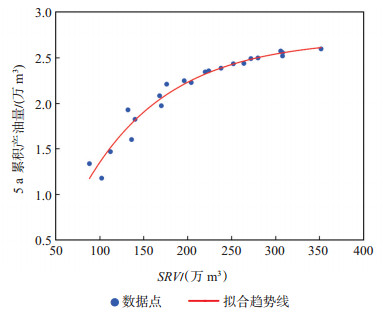
图 8反映了22种裂缝分布方案对应的5 a累积产油量和SRV的关系，随SRV增大，油井累积产油量增幅逐渐变缓，因此现场压裂并不能一味地追求较高的SRV。这是因为，SRV较小时，裂缝条数较少，不同裂缝段之间的区域向改造体的线性流供液时间越长，而当SRV增大时，对应的裂缝条数增多，缝间干扰加剧，累积产油量增幅变缓。因此，矿场实际生产时为了提高生产效率，除了增大裂缝条数提高SRV外，不能使裂缝分布过密，导致缝间干扰而降低开发效果。

图 8

Fig. 8

下载eps/tif图 图 8 储层改造体积与油井产能的关系 Fig. 8 Relationship between SRV and oil well cumulative productivity

(1) 基于三线性流和五线性流分区模型，建立了致密油藏分段多簇压裂水平井产能模型，模型不仅考虑了致密油藏低速非达西流动和裂缝应力敏感特征，而且考虑了分段多簇压裂段间渗流场和簇间渗流场的差异性，因而更符合矿场实际生产情况。

(2) 低速非达西流动和裂缝渗透率应力敏感均会影响油井的产能大小，因此在对致密油藏分段多簇压裂水平井进行产能评价时需要考虑这2个因素的影响。

(3) 致密油藏分段多簇压裂水平井的产能随裂缝条数和储层改造体积(SRV)的增大呈现先增大而后增幅变缓的趋势，这是因为当裂缝条数过多后，缝间干扰现象增强。所以，矿场在对致密油藏水平井分段多簇压裂实际施工设计时，不能一味地增加压裂段数或簇数，而是应该选择适当的布缝方式，经济有效地提高油井产能。