2. 中国石油大港油田分公司 采油工艺研究院, 天津 300280
2. Research Institute of Oil Production Technology, PetroChina Dagang Oilfield Company, Tianjin 300280, China
页岩气藏作为重要的非常规油气资源之一,近年来已成为国内外学者研究的热点[1-2]。页岩气存在吸附解吸、基质中扩散、基质向裂缝间窜流和裂缝中渗流等多种气体运移机制[3-4]。页岩储层渗透率极低,需对其进行水力压裂改造[5-7]。压裂改造可形成高导流区,把包括裂缝在内的这一区域称为改造储层体积(SRV)[8-9],其形态可简化为一椭圆形区域[10]。一些学者[11-12]利用复合气藏模型分析了考虑椭圆SRV的压裂井压力变化特征,但都未考虑基质向裂缝间的窜流。Zhang等[11]建立了考虑椭圆SRV的双重介质页岩气藏压裂井复合模型,依照Fick第一扩散定律在基质中拟稳态扩散。姜瑞忠等[12]提出依照Fick第二扩散定律的压裂改造复合页岩气藏压力分析方法,运用椭圆坐标系模型,综合分析了非稳态扩散、解吸、渗流等传质机理。页岩气藏渗透率低,储层表现出很强的应力敏感性,其对压力的影响不容忽视[13]。尹洪军等[14]研究了均质页岩气藏垂直裂缝井椭圆流压力动态问题,模型考虑了应力敏感效应的影响,但也未涉及SRV的分析。
综上所述,目前还未有考虑应力敏感性、基质向裂缝间非稳态窜流、椭圆SRV等的数学模型。本次研究根据页岩气吸附解吸、Knudsen扩散、非稳态窜流和渗流等多种气体运移机制对压力的影响,来建立综合应力敏感性和椭圆SRV的复合页岩气藏压裂井试井模型,并利用Mathieu函数、Pedrosa变量代换、正则摄动理论等方法对数学模型进行求解,以期提出的压力动态分析方法可为水力压裂开采页岩气藏提供一定的理论支持。
1 物理模型考虑SRV的压裂改造页岩气藏模型如图 1所示,内外两区均为椭圆形,外区为原始储层,内区为压裂改造区(SRV),其孔隙度和渗透率较外区高。模型假设如下:①外区边界无限大,内区半径为ξ1;②气藏储层厚度为h,初始地层压力为Pi;③基质假设为球状,半径为Rm,基质中存在吸附气和自由气,裂缝中为自由气;④压裂井位于气藏中心,以定产量qsc生产;⑤考虑基质中气体的吸附解吸,气体扩散满足Knudsen定律,并且考虑从基质到裂缝间的非稳态窜流;⑥只考虑裂缝受应力敏感的影响,由于应力敏感主要发生在近井地带,只在内区考虑其对渗流的影响[15];⑦忽略重力和毛管压力的影响。
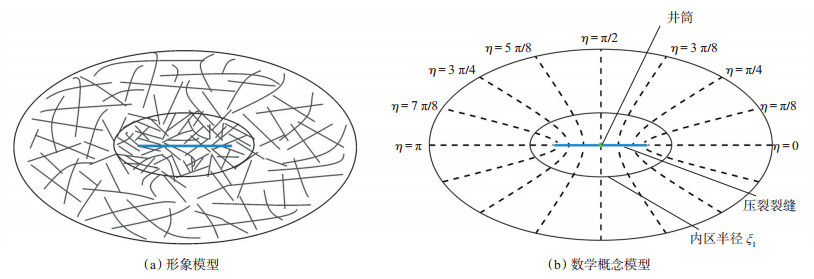
|
下载eps/tif图 图 1 考虑椭圆SRV的复合页岩气藏压裂井模型 Fig. 1 Fractured well model in composite shale gas reservoir considering elliptical SRV |
页岩气按照Knudsen扩散模型在纳米级孔隙中扩散[16],由于浓度差作用的扩散所产生的质量通量为
| $ {J_{\rm{k}}}= - D{M_{\rm{g}}}\frac{{\partial {C_{\rm{m}}}}}{{\partial {r_{\rm{m}}}}} $ | (1) |
式中:Jk为由于浓度差作用的扩散所产生的质量通量,kg/(m2·s);D为扩散系数,m2/s;Mg为气体摩尔质量,kg/mol;Cm为基质中气体浓度,mol/m3;rm为基质中径向距离,m。
气体状态方程为
| $ {p_{\rm{m}}}V=ZnRT $ | (2) |
式中:pm为基质压力,Pa;V为气体体积,m3;Z为气体压缩因子;n为气体物质的量,mol;R为通用气体常数,Pa·m3/(mol·K);T为气藏储层温度,K。
由式(2)可求得气体浓度为
| $ {C_{\rm{m}}}=\frac{n}{V}=\frac{{{p_{\rm{m}}}}}{{ZRT}} $ | (3) |
气体压缩系数表达式为
| $ {c_{{\rm{gm}}}}=\frac{1}{\rho }\frac{{\partial \rho }}{{\partial {p_{\rm{m}}}}}=\frac{1}{{{p_{\rm{m}}}}} - \frac{1}{Z}\frac{{\partial Z}}{{\partial {p_{\rm{m}}}}} $ | (4) |
式中:cgm为基质中气体压缩系数,Pa-1;ρ为气体密度,kg/m3。
将式(3)代入式(1)并联立式(4)整理可得
| $ {J_{\rm{k}}}= - \frac{{D{p_{\rm{m}}}{M_{\rm{g}}}{c_{{\rm{gm}}}}}}{{ZRT}}\frac{{\partial {p_{\rm{m}}}}}{{\partial {r_{\rm{m}}}}} $ | (5) |
压力差作用的渗流所产生的质量通量为
| $ {J_{\rm{p}}}= - \frac{{\rho {k_{\rm{m}}}}}{\mu }\frac{{\partial {p_{\rm{m}}}}}{{\partial {r_{\rm{m}}}}} $ | (6) |
式中:Jp为压力差作用的渗流所产生的质量通量,kg/(m2·s);km为基质渗透率,mD;μ为气体黏度,mPa∙s。
式(2)变形可得
| $ \rho =\frac{{{p_{\rm{m}}}{M_{\rm{g}}}}}{{ZRT}} $ | (7) |
则浓度差和压力差共同作用所产生的质量通量为
| $ J={J_{\rm{p}}}+ {J_{\rm{k}}}= - \frac{\rho }{\mu }\left( {{k_{\rm{m}}}+ D\mu {c_{{\rm{gm}}}}} \right)\frac{{\partial {p_{\rm{m}}}}}{{\partial {r_{\rm{m}}}}} $ | (8) |
定义表观渗透率如下
| $ {k_{\rm{a}}}={k_{\rm{m}}}+ D\mu {c_{{\rm{gm}}}} $ | (9) |
式中:ka为基质的表观渗透率,mD。
球状基质表面处的质量流速[17]为
| $ v= - \frac{{\rho {k_{\rm{a}}}}}{\mu }{\left. {\frac{{\partial {p_{\rm{m}}}}}{{\partial {r_{\rm{m}}}}}} \right|_{{r_{\rm{m}}}={R_{\rm{m}}}}} $ | (10) |
式中:v为气体质量流速,kg/(m2·s);Rm为基质块半径,m。
单位体积基质在单位时间内向裂缝的非稳态窜流量为qm,基质球面处的流速等于单位时间基质的流出量与基质表面积的比值,即
| $ v=\frac{{\frac{4}{3}\pi R_{\rm{m}}^3{q_{\rm{m}}}}}{{4\pi R_{\rm{m}}^2}}=\frac{1}{3}{R_{\rm{m}}}{q_{\rm{m}}} $ | (11) |
式中:qm为气体窜流质量流量,kg/(m3·s)。
将式(11)代入式(10)整理可得
| $ {q_{\rm{m}}}= - \frac{{3\rho }}{{{R_{\rm{m}}}}}\frac{{{k_{\rm{a}}}}}{\mu }{\left. {\frac{{\partial {p_{\rm{m}}}}}{{\partial {r_{\rm{m}}}}}} \right|_{{r_{\rm{m}}}={R_{\rm{m}}}}} $ | (12) |
吸附气解吸速度为[18]
| $ {q_{\rm{d}}}=\rho \left( {1 - {\varphi _{\rm{f}}} - {\varphi _{\rm{m}}}} \right){G_{\rm{L}}}\frac{{{p_{\rm{L}}}}}{{{{\left( {{p_{\rm{L}}}+ {p_{\rm{m}}}} \right)}^2}}}\frac{{\partial {p_{\rm{m}}}}}{{\partial t}} $ | (13) |
式中:qd为气体解吸质量流速,kg/(m3·s);φf为裂缝孔隙度,%;φm为基质孔隙度,%;GL为兰格缪尔体积,m3/m3;pL为兰格缪尔压力,Pa;t为时间,s。
引入气体拟压力表达式
| $ \psi =\int_{{p_{\rm{i}}}}^p {\frac{{2p}}{{\mu Z}}} {\rm{d}}p $ | (14) |
式中:ψ为拟压力,Pa/(mPa·s);
内区裂缝考虑应力敏感性,渗透率模量定义如下
| $ \gamma =\frac{1}{{{k_{{\rm{f1}}}}}}\frac{{d{k_{{\rm{f1}}}}}}{{d{\psi _{{\rm{f1}}}}}} $ | (15) |
式中:γ为渗透率模量,mPa·s/Pa2;kf1为内区裂缝渗透率,mD;γf1为内区裂缝拟压力,Pa2/(mPa·s)。式(15)可变形为
| $ \int_{{k_{{\rm{f1}}}}}^{{k_{{\rm{f1i}}}}} {\frac{1}{{{k_{{\rm{f1}}}}}}} {\rm{d}}{k_{{\rm{f1}}}}=\int_{{\psi _{{\rm{f1}}}}}^{{\psi _{\rm{i}}}} \gamma {\rm{d}}{\psi _{{\rm{f1}}}} $ | (16) |
求解式(16)可得
| $ {k_{{\rm{f1}}}}={k_{{\rm{f1i}}}}{e^{ - \gamma \left( {{\psi _{\rm{i}}} - {\psi _{{\rm{f1}}}}} \right)}} $ | (17) |
则内区裂缝的渗流方程为
| $ \begin{array}{l} \frac{\partial }{{\partial x}}\left[ {{e^{ - \gamma \left( {{\psi _{\rm{i}}} - {\psi _{{\rm{f1}}}}} \right)}}\frac{{\partial {\psi _{{\rm{f1}}}}}}{{\partial x}}} \right]+ \frac{\partial }{{\partial y}}\left[ {{e^{ - \gamma \left( {{\psi _{\rm{i}}} - {\psi _{{\rm{f1}}}}} \right)}}\frac{{\partial {\psi _{{\rm{f1}}}}}}{{\partial y}}} \right]=\\ \;\;\;\;\;\;\;\;\;\;\frac{{{\varphi _{{\rm{f1}}}}\mu {c_{{\rm{tf1}}}}}}{{{k_{{\rm{f1i}}}}}}\frac{{\partial {\psi _{{\rm{f1}}}}}}{{\partial t}}+ \frac{3}{{{R_{{\rm{m}}1}}}}\frac{{{k_{a1}}}}{{{k_{{\rm{f1i}}}}}}{\left. {\frac{{\partial {\psi _{{\rm{m}}1}}}}{{\partial {r_{{\rm{m}}1}}}}} \right|_{{r_{{\rm{m1}}}}={R_{{\rm{m1}}}}}} \end{array} $ | (18) |
式中:式中:φf1为内区裂缝孔隙度,%;ctf1为内区裂缝总压缩系数,Pa-1;Rm1为内区基质块半径,m;ka1为内区基质的表观渗透率,mD;γm1为内区基质拟压力,Pa2/(mPa·s);rm1为内区基质中径向距离,m。
内区基质的渗流方程为
| $ \begin{array}{l} \frac{1}{{r_{{\rm{m}}1}^2}}\frac{\partial }{{\partial {r_{{\rm{m}}1}}}}\left( {r_{{\rm{m}}1}^2\frac{{\partial {\psi _{{\rm{m}}1}}}}{{\partial {r_{{\rm{m}}1}}}}} \right)=\frac{{{\varphi _{{\rm{m}}1}}\mu {c_{{\rm{tm1}}}}}}{{{k_{a1}}}}\frac{{\partial {\psi _{{\rm{m}}1}}}}{{\partial t}}+ \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{\varphi _{{\rm{m}}1}}\mu {c_{{\rm{d}}1}}}}{{{k_{a1}}}}\frac{{\partial {\psi _{{\rm{m}}1}}}}{{\partial t}} \end{array} $ | (19) |
式中:φm1为内区基质孔隙度,%;ctm1为内区基质总压缩系数,Pa-1;ka1为内区基质的表观渗透率,mD;cd1为内区考虑解吸的附加压缩系数,Pa-1,表达式如下
| $ {c_{\rm{d}}}=\frac{{2T{p_{{\rm{sc}}}}}}{{{\varphi _{\rm{m}}}\mu {T_{{\rm{sc}}}}}}\frac{{\left( {1 - {\varphi _{\rm{f}}} - {\varphi _{\rm{m}}}} \right){G_{\rm{L}}}{\psi _{\rm{L}}}}}{{{{\left( {{\psi _{\rm{L}}}+ {\psi _{\rm{m}}}} \right)}^2}}} $ | (20) |
式中:cd为考虑解吸的附加压缩系数,Pa-1;psc为标准条件下的压力,Pa;Tsc为标准条件下的温度,K;ψL为兰格缪尔拟压力,Pa2/(mPa·s)。
定义无因次参数如下:
式中:L为参考长度,m;qsc为恒定地面气体产量,m3/s;C为井筒存储系数,m3/Pa;h为气藏厚度,m;β为内外区储容比;θ为渗透率比;φm2为外区基质孔隙度,%;ctm2为外区基质总压缩系数,Pa-1;φf2为外区裂缝孔隙度,%;ctf2为外区裂缝总压缩系数,Pa-1;ωf为裂缝储容比;ωm为裂缝储容比;ωd为考虑解吸的储容比;λ为窜流系数;M为流度比;kf2为外区裂缝渗透率,mD。
将无因次参数代入式(18)—(19)中,得无因次条件下裂缝和基质的渗流方程分别为
| $ \begin{array}{l} \frac{{{\partial ^2}{\psi _{{\rm{f1D}}}}}}{{\partial x_{\rm{D}}^2}} - {\gamma _{\rm{D}}}{\left( {\frac{{\partial {\psi _{{\rm{f1D}}}}}}{{\partial {x_{\rm{D}}}}}} \right)^2}+ \frac{{{\partial ^2}{\psi _{{\rm{f1D}}}}}}{{\partial y_{\rm{D}}^2}} - {\gamma _{\rm{D}}}{\left( {\frac{{\partial {\psi _{{\rm{f1D}}}}}}{{\partial {y_{\rm{D}}}}}} \right)^2}=\\ \;\;\;\;\;\;\;\;\;{e^{{\gamma _D}{\psi _{{\rm{f1D}}}}}}\left( {{\omega _{{\rm{f1}}}}\frac{{\partial {\psi _{{\rm{f1D}}}}}}{{\partial {t_{\rm{D}}}}}+ 3{\lambda _1}{\theta _1}{{\left. {\frac{{\partial {\psi _{{\rm{m}}1{\rm{D}}}}}}{{\partial {r_{{\rm{m1D}}}}}}} \right|}_{{r_{{\rm{m1D}}}}=1}}} \right) \end{array} $ | (21) |
| $ \frac{1}{{r_{{\rm{m1D}}}^2}}\frac{\partial }{{\partial {r_{{\rm{m1D}}}}}}\left( {r_{{\rm{m1D}}}^2\frac{{\partial {\psi _{{\rm{m1D}}}}}}{{\partial {r_{{\rm{m1D}}}}}}} \right)=\frac{{{\omega _{{\rm{m}}1}}}}{{{\lambda _1}{\theta _1}}}\frac{{\partial {\psi _{{\rm{m1D}}}}}}{{\partial {t_{\rm{D}}}}}+ \frac{{{\omega _{{\rm{d}}1}}}}{{{\lambda _1}{\theta _1}}}\frac{{\partial {\psi _{{\rm{m1D}}}}}}{{\partial {t_{\rm{D}}}}} $ | (22) |
式中:ωf1为内区裂缝储容比;λ1为内区窜流系数;θ1为内区渗透率比;ωm1为内区基质储容比;ωd1为内区考虑解吸的储容比。
利用Pedrosa变量代换处理裂缝渗流方程的强非线性[19],表达式如下
| $ {\psi _{{\rm{f1D}}}}\left( {{x_{\rm{D}}}, {y_{\rm{D}}}, {t_{\rm{D}}}} \right)= - \frac{1}{{{\gamma _{\rm{D}}}}}\ln \left[ {1 - {\gamma _{\rm{D}}}{\chi _{{\rm{1D}}}}\left( {{x_{\rm{D}}}, {y_{\rm{D}}}, {t_{\rm{D}}}} \right)} \right] $ | (23) |
式中:χ1D为摄动变换函数。
将式(23)代入式(21)可得
| $ \begin{array}{l} \frac{1}{{1 - {\gamma _{\rm{D}}}{\chi _{1{\rm{D}}}}}}\frac{{{\partial ^2}{\chi _{1{\rm{D}}}}}}{{\partial x_{\rm{D}}^2}}+ \frac{{\partial {\chi _{1{\rm{D}}}}}}{{\partial {x_{\rm{D}}}}}\frac{1}{{{{\left( {1 - {\gamma _{\rm{D}}}{\chi _{{\rm{1D}}}}} \right)}^2}}}{\gamma _{\rm{D}}}\frac{{\partial {\chi _{1{\rm{D}}}}}}{{\partial {x_{\rm{D}}}}} - {\gamma _{\rm{D}}}{\left( {\frac{1}{{1 - {\gamma _{\rm{D}}}{\chi _{1{\rm{D}}}}}}\frac{{\partial {\chi _{1{\rm{D}}}}}}{{\partial {x_{\rm{D}}}}}} \right)^2}+ \frac{1}{{1 - {\gamma _{\rm{D}}}{\chi _{1{\rm{D}}}}}}\frac{{{\partial ^2}{\chi _{1{\rm{D}}}}}}{{\partial y_{\rm{D}}^2}}+ \frac{{\partial {\chi _{1{\rm{D}}}}}}{{\partial {y_{\rm{D}}}}}.\\ \frac{1}{{{{\left( {1 - {\gamma _{\rm{D}}}{\chi _{1{\rm{D}}}}} \right)}^2}}}{\gamma _{\rm{D}}}\frac{{\partial {\chi _{1{\rm{D}}}}}}{{\partial {y_{\rm{D}}}}} - {\gamma _{\rm{D}}}{\left( {\frac{1}{{1 - {\gamma _{\rm{D}}}{\chi _{1{\rm{D}}}}}}\frac{{\partial {\chi _{1{\rm{D}}}}}}{{\partial {y_{\rm{D}}}}}} \right)^2}\\ ={e^{ - \ln \left( {1 - {\gamma _{\rm{D}}}{\chi _{_{1{\rm{D}}}}}} \right)}}\left( {{\omega _{{\rm{f}}1}}\frac{1}{{1 - {\gamma _{\rm{D}}}{\chi _{1{\rm{D}}}}}}\frac{{\partial {\chi _{1{\rm{D}}}}}}{{\partial {t_{\rm{D}}}}}+ 3{\lambda _1}{\theta _1}{{\left. {\frac{{\partial {\psi _{{\rm{m}}1{\rm{D}}}}}}{{\partial {r_{{\rm{m}}1{\rm{D}}}}}}} \right|}_{{r_{{\rm{m}}1{\rm{D}}}}=1}}} \right) \end{array} $ | (24) |
将式(24)进行整理,等式两边约去相同项可得
| $ \frac{{{\partial ^2}{\chi _{1{\rm{D}}}}}}{{\partial x_{\rm{D}}^2}}+ \frac{{{\partial ^2}{\chi _{1{\rm{D}}}}}}{{\partial y_{\rm{D}}^2}}=\frac{{{\omega _{{\rm{f1}}}}}}{{1 - {\gamma _{\rm{D}}}{\chi _{1{\rm{D}}}}}}\frac{{\partial {\chi _{1{\rm{D}}}}}}{{\partial {t_{\rm{D}}}}}+ 3{\lambda _1}{\theta _1}{\left. {\frac{{\partial {\psi _{{\rm{m}}1{\rm{D}}}}}}{{\partial {r_{{\rm{m}}1{\rm{D}}}}}}} \right|_{{r_{{\rm{m}}1{\rm{D}}}}=1}} $ | (25) |
由正则摄动理论,有
| $ \frac{1}{{1 - {\gamma _{\rm{D}}}{\chi _{{\rm{1D}}}}}}=1+ {\gamma _{\rm{D}}}{\chi _{{\rm{1D}}}}+ \gamma _{\rm{D}}^2\chi _{{\rm{1D}}}^2+ L $ | (26) |
| $ - \frac{1}{{{\gamma _{\rm{D}}}}}\ln \left( {1 - {\gamma _{\rm{D}}}{\chi _{{\rm{1D}}}}} \right)={\chi _{{\rm{1D}}}}+ \frac{1}{2}{\gamma _{\rm{D}}}\chi _{{\rm{1D}}}^2+ L $ | (27) |
无因次渗透率模量通常很小(γD≪1),0阶近似解满足工程精度要求,式(25)变为
| $ \frac{{{\partial ^2}{\chi _{1{\rm{D}}}}}}{{\partial x_{\rm{D}}^2}}+ \frac{{{\partial ^2}{\chi _{1{\rm{D}}}}}}{{\partial y_{\rm{D}}^2}}={\omega _{{\rm{f1}}}}\frac{{\partial {\chi _{1D}}}}{{\partial {t_{\rm{D}}}}}+ 3{\lambda _1}{\theta _1}{\left. {\frac{{\partial {\psi _{{\rm{m}}1{\rm{D}}}}}}{{\partial {r_{{\rm{m}}1{\rm{D}}}}}}} \right|_{{r_{{\rm{m}}1{\rm{D}}}}=1}} $ | (28) |
式(28)、(22)拉普拉斯变换后为
| $ \frac{{{\partial ^2}{{\bar \chi }_{1{\rm{D}}}}}}{{\partial x_{\rm{D}}^2}}+ \frac{{{\partial ^2}{{\bar \chi }_{1{\rm{D}}}}}}{{\partial y_{\rm{D}}^2}}={\omega _{{\rm{f1}}}}s{{\bar \chi }_{1{\rm{D}}}}+3{\lambda _1}{\theta _1}{\left. {\frac{{\partial {{\bar \psi }_{{\rm{m}}1{\rm{D}}}}}}{{\partial {r_{{\rm{m}}1{\rm{D}}}}}}} \right|_{{r_{{\rm{m}}1{\rm{D}}}}=1}} $ | (29) |
| $ \frac{1}{{r_{{\rm{m1D}}}^2}}\frac{\partial }{{\partial {r_{{\rm{m1D}}}}}}\left( {r_{{\rm{m1D}}}^2\frac{{\partial {{\bar \psi }_{{\rm{m1D}}}}}}{{\partial {r_{{\rm{m1D}}}}}}} \right){\rm{=}}\frac{{{\omega _{{\rm{m}}1}}+ {\omega _{{\rm{d}}1}}}}{{{\lambda _1}{\theta _1}}}s{\bar \psi _{{\rm{m1D}}}} $ | (30) |
式中:s为拉普拉斯变量。
球形基质的初始及内外边界条件经无因次化、Pedrosa变量代换及拉普拉斯变换后为
| $ {\left. {{{\bar \psi }_{{\rm{m1D}}}}} \right|_{{t_{\rm{D}}}=0}}=0 $ | (31) |
| $ \frac{{\partial {{\bar \psi }_{{\rm{m}}1{\rm{D}}}}}}{{\partial {r_{{\rm{m}}1{\rm{D}}}}}}\left| {_{{r_{{\rm{m}}1{\rm{D}}}}=0}} \right.{\rm{=}}0 $ | (32) |
| $ {{\bar \psi }_{{\rm{m}}1{\rm{D}}}}\left| {_{{r_{{\rm{m}}1{\rm{D}}}}=1}} \right.{\rm{=}}{{\bar \chi }_{1{\rm{D}}}} $ | (33) |
将式(31)—(33)与式(30)联立可得
| $ \begin{array}{l} \frac{{\partial {{\bar \psi }_{{\rm{m}}1{\rm{D}}}}}}{{\partial {r_{{\rm{m}}1{\rm{D}}}}}}\left| {_{{r_{{\rm{m}}1{\rm{D}}}}=1}} \right.=\left[ {\sqrt {\frac{{{\omega _{{\rm{m}}1}}+ {\omega _{{\rm{d}}1}}}}{{{\lambda _1}{\theta _1}}}s} } \right. \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\coth \left( {\sqrt {\frac{{{\omega _{{\rm{m}}1}}+ {\omega _{{\rm{dl}}}}}}{{{\lambda _1}{\theta _1}}}s} } \right) - 1]{{\bar \chi }_{{\rm{1D}}}} \end{array} $ | (34) |
将式(34)代入式(29)可得
| $ \frac{{{\partial ^2}{{\bar \chi }_{1{\rm{D}}}}}}{{\partial x_{\rm{D}}^2}}+ \frac{{{\partial ^2}{{\bar \chi }_{1{\rm{D}}}}}}{{\partial y_{\rm{D}}^2}}=4{f_1}{{\bar \chi }_{1D}} $ | (35) |
式中:
笛卡尔坐标转换为椭圆坐标的方法为
| $ \left\{ {\begin{array}{*{20}{l}} {{x_D}=\cosh \xi \cos \eta }\\ {{y_D}=\sinh \xi \sin \eta } \end{array}} \right. $ | (36) |
式中:ξ,η为椭圆坐标。
将式(36)代入式(35)可得椭圆坐标系的渗流方程为
| $ \frac{{\partial {{\bar \chi }_{1D}}}}{{\partial {\xi ^2}}}+ \frac{{{\partial ^2}{{\bar \chi }_{1{\rm{D}}}}}}{{\partial {\eta ^2}}}=2(\cosh 2\xi - \cos 2\eta ){f_1}{{\bar \chi }_{1D}} $ | (37) |
外区无因次化及拉普拉斯变换后的裂缝和基质渗流方程分别为
| $ \begin{array}{l} \frac{{{\partial ^2}{{\bar \psi }_{{\rm{f2D}}}}}}{{\partial x_{\rm{D}}^2}}+ \frac{{{\partial ^2}{{\bar \psi }_{{\rm{f}}2{\rm{D}}}}}}{{\partial y_{\rm{D}}^2}}=\frac{{M{\omega _{{\rm{f}}2}}}}{\beta }s{{\bar \psi }_{{\rm{f}}2{\rm{D}}}}+ \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;3{\lambda _2}{\theta _2}\frac{{\partial {{\bar \psi }_{m2{\rm{D}}}}}}{{\partial {r_{2{\rm{mD}}}}}}\left| {_{{r_{{\rm{m}}2{\rm{D}}}}=1}} \right. \end{array} $ | (38) |
| $ \begin{array}{l} \frac{1}{{r_{{\rm{m}}2{\rm{D}}}^2}}\frac{\partial }{{\partial {r_{{\rm{m}}2{\rm{D}}}}}}\left( {r_{{\rm{m}}2{\rm{D}}}^2\frac{{{\partial ^2}{{\bar \psi }_{{\rm{m}}2{\rm{D}}}}}}{{\partial {r_{{\rm{m}}2{\rm{D}}}}}}} \right)=\frac{{M{\omega _{{\rm{m}}2}}}}{{\beta {\lambda _2}{\theta _2}}}s{{\bar \psi }_{{\rm{m}}2{\rm{D}}}}+ \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{M{\omega _{{\rm{d}}2}}}}{{\beta {\lambda _2}{\theta _2}}}s{{\bar \psi }_{{\rm{m}}2{\rm{D}}}} \end{array} $ | (39) |
式中:ωf2为外区裂缝储容比;λ2为外区窜流系数;θ2为外区渗透率比;ωm2为外区基质储容比;ωd2为外区考虑解吸的储容比。
利用与内区相同的求解方法对式(38)、(39)进行求解,并利用式(36)将坐标转换为椭圆坐标为
| $ \frac{{{\partial ^2}{{\bar \psi }_{{\rm{f2D}}}}}}{{\partial {\xi ^2}}}+ \frac{{{\partial ^2}{{\bar \psi }_{{\rm{f2D}}}}}}{{\partial {\eta ^2}}}=2(\cosh 2\xi - \cos 2\eta ){f_2}{{\bar \psi }_{{\rm{f2D}}}} $ | (40) |
式中:
定压内边界条件为
| $ {\left. {{{\bar \chi }_{{\rm{1D}}}}} \right|_{\xi ={\xi _{\rm{w}}}}}=\frac{1}{s} $ | (41) |
式中:ξw为椭圆坐标下井筒半径。
无限大外边界条件为
| $ {\left. {{{\bar \psi }_{{\rm{f2D}}}}} \right|_{\xi =\infty }}=0 $ | (42) |
ξ=ξ1时,内外区压力和流量相等,交界面条件为
| $ {{{\left. {{{\bar \chi }_{1{\rm{D}}}}} \right|}_{\xi ={\xi _1}}}={{\left. {{{\bar \psi }_{{\rm{f}}2{\rm{D}}}}} \right|}_{\xi ={\xi _1}}}} $ | (43) |
| $ {{{\left. {\frac{{\partial {{\bar \chi }_{1{\rm{D}}}}}}{{\partial \xi }}} \right|}_{\xi ={\xi _1}}}=\frac{1}{M}{{\left. {\frac{{\partial {{\bar \psi }_{{\rm{f}}2D}}}}{{\partial \xi }}} \right|}_{\xi ={\xi _1}}}} $ | (44) |
根据式(42)和Mathieu函数性质[20]得式(37),(40)的解为
| $ \begin{array}{l} {{\bar \chi }_{1{\rm{D}}}}\left( {\xi , \eta , - {f_1}} \right)=\sum\limits_{n=0}^\infty {{D_{{\rm{2n}}}}} G{e_{{\rm{2n}}}}\left( {\xi , - {f_1}} \right)c{e_{{\rm{2n}}}}\left( {\eta , - {f_1}} \right)+ \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{I_{{\rm{2n}}}}U{e_{{\rm{2n}}}}\left( {\xi , - {f_1}} \right)c{e_{{\rm{2n}}}}\left( {\eta , - {f_1}} \right) \end{array} $ | (45) |
| $ {{{\bar \psi }_{{\rm{f}}2D}}\left( {\xi , \eta , - {f_2}} \right)=\sum\limits_{n=0}^\infty {{H_{{\rm{2n}}}}} U{e_{{\rm{2n}}}}\left( {\xi , - {f_2}} \right)c{e_{{\rm{2n}}}}\left( {\eta , - {f_2}} \right)} $ | (46) |
式中:ce2n为2n阶第一类Mathieu函数角函数;Ge2n为2n阶第一类Mathieu函数径函数;Ue2n为2n阶第二类Mathieu函数径函数。
由式(41),(43)和(44)得
| $ {{B_{1, 1}}{D_{{\rm{2n}}}}+ {B_{1, 2}}{I_{{\rm{2n}}}}=1} $ | (47) |
| $ {{B_{2, 1}}{D_{{\rm{2n}}}}+ {B_{2, 2}}{I_{{\rm{2n}}}}+ {B_{2, 3}}{H_{{\rm{2n}}}}=0} $ | (48) |
| $ {{B_{3, 1}}{D_{{\rm{2n}}}}+ {B_{3, 2}}{I_{{\rm{2n}}}}+ {B_{3, 3}}{H_{{\rm{2n}}}}=0} $ | (49) |
式中:
联立式(47)—(49)可得D2n,I2n和H2n,Pedrosa变量代换后的产量为
| $ {{\bar q}_{\rm{D}}} = - \frac{1}{{2\pi }}\int_0^{2\pi } {{{\left( {\frac{{\partial {{\bar \chi }_{{\rm{1D}}}}}}{{\partial \xi }}} \right)}_{\xi ={\xi _{\rm{w}}}}}} {\rm{d}}\eta $ | (50) |
式中:
由角度Mathieu函数的性质[20],有下式
| $ \int_0^{2\pi } c {e_{{\rm{2n}}}}\left( {\eta , - {f_1}} \right){\rm d}\eta = {( - 1)^n}2\pi A_0^{{\rm{2n}}} $ | (51) |
将式(51)代入式(50)得
| $ \begin{array}{l} {{\bar q}_{\rm{D}}} = \sum\limits_{n = 0}^\infty {{{( - 1)}^{n + 1}}} A_0^{2{\rm{n}}}\left[ {{D_{2{\rm{n}}}}Ge_{2{\rm{n}}}^\prime \left( {{\xi _{\rm{w}}}, - {f_1}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;{I_{2{\rm{n}}}}Ue_{2{\rm{n}}}^\prime \left( {{\xi _{\rm{w}}}, - {f_1}} \right)] \end{array} $ | (52) |
拉氏空间下定产量时的井底压力解满足[21]
| $ {{\bar \chi }_{{\rm{wD}}}} = \frac{1}{{{s^2}{{\bar q}_{\rm{D}}}}} $ | (53) |
考虑井筒存储效应和表皮系数时,式(53)变为
| $ {{\bar \chi }_{{\rm{wD}}}}\left( {S, {C_{\rm{D}}}} \right) = \frac{{s{{\bar \chi }_{{\rm{wD}}}} + S}}{{s + {C_{\rm{D}}}{s^2}\left[ {s{{\bar \chi }_{{\rm{wD}}}} + S} \right]}} $ | (54) |
式中:S为表皮系数。
利用Stehfest数值反演法[22]可得真实空间下的压力χwD,则考虑应力敏感的井底拟压力为
| $ {m_{{\rm{wD}}}} = - \frac{1}{{{\gamma _{\rm{D}}}}}\ln \left( {1 - {\gamma _{\rm{D}}}{\chi _{{\rm{wD}}}}} \right) $ | (55) |
图 2为考虑椭圆SRV的复合页岩气藏拟压力及导数典型曲线,基本参数取值为:CD=10,S=0.1,ξ=11,kf1=0.02 mD,kf2=0.005 mD,D=10-6(m2/s),cd=0.013 MPa-1。依据曲线形态可将流动阶段划分为9段:①井筒存储阶段,拟压力及导数曲线重合,斜率为1;②表皮因子影响阶段,导数曲线形状为一驼峰;③内区裂缝径向流阶段,表现为值为0.5的水平线;④内区窜流阶段,导数曲线为一凹子;⑤内区整体径向流阶段,导数曲线水平;⑥过渡流阶段,压力传播到内外区交界面处;⑦外区裂缝径向流阶段;⑧外区窜流阶段;⑨储层整体径向流阶段。
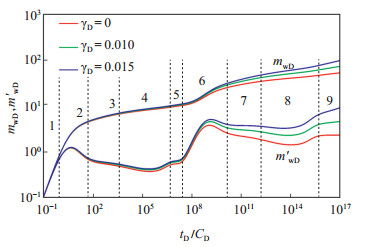
|
下载eps/tif图 图 2 拟压力及导数典型曲线 Fig. 2 Typical curves of pseudo-pressure and derivative |
对渗透率模量、SRV半径、外区裂缝渗透率、扩散系数、解吸压缩系数等参数进行敏感性分析,基本参数取值为:CD=10,S=0.1,γD=0.01,ξ=11,kf1=0.02 mD,kf2=0.005 mD,D=10-6(m2/s),cd=0.013 MPa-1。
5.1 渗透率模量影响图 2反映了渗透率模量γD对复合页岩气藏压力的影响,渗透率模量的增加使得拟压力及导数曲线上升,并且外区曲线所受到的影响更加强烈。在整体径向流阶段,导数曲线开始上翘,这是应力敏感效应产生的典型曲线特征。当气藏考虑应力敏感性时,储层渗透率随压力的减小而降低,页岩气的流动阻力增大,导致流动所需压差增大。
5.2 SRV半径影响图 3反映了SRV半径ξ1对复合页岩气藏压力的影响,SRV半径对内区整体径向流阶段和过渡流阶段产生的影响较大。随SRV半径的增大,拟压力曲线向下移动,导数曲线向右移动,当SRV半径足够小时,内区整体径向流阶段消失。因为SRV半径越大,储层改造的体积越大,越有利于气井生产的进行,气井生产所需的压差减小。
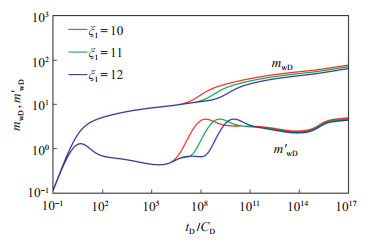
|
下载eps/tif图 图 3 SRV半径对复合页岩气藏压力的影响 Fig. 3 Influence of SRV radius on pressure of composite shale gas reservoir |
图 4反映了外区裂缝渗透率kf2对复合页岩气藏压力的影响,外区裂缝渗透率影响了内区整体径向流阶段之后的曲线形态。外区裂缝渗透率的增加与流度比的减小相对应,使得外区拟压力及导数曲线下移。流度比减小,则外区未改造的原始储层条件相对内区变好,外区流动所需的压降减小,则压裂改造提高裂缝渗透率可以很好地提高开发效果。
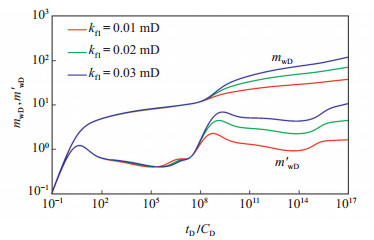
|
下载eps/tif图 图 4 外区裂缝渗透率对复合页岩气藏压力的影响 Fig. 4 Influence of fracture permeability in outer zone on pressure of composite shale gas reservoir |
图 5反映了扩散系数D对复合页岩气藏压力的影响,扩散系数主要影响内外区窜流阶段。扩散系数的增加导致了页岩基质表观渗透率的增加,使得窜流系数增大,窜流阶段提前,在导数曲线上表现为内外区凹子向左移动,拟压力曲线向下移动,气井生产所需的压差减小。
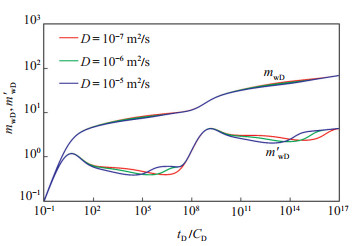
|
下载eps/tif图 图 5 扩散系数对复合页岩气藏压力的影响 Fig. 5 Influence of diffusion coefficient on pressure of composite shale gas reservoir |
图 6反映了解吸压缩系数cd对复合页岩气藏压力的影响,解吸压缩系数影响内区裂缝径向流之后的阶段。解吸压缩系数增大使得考虑解吸的储容比ωd增大,窜流阶段的凹子变深且变宽,影响了导数曲线窜流阶段前后径向流的持续时间,解吸压缩系数增大导致过渡流阶段右移,驼峰升高,气井生产所需压差降低。
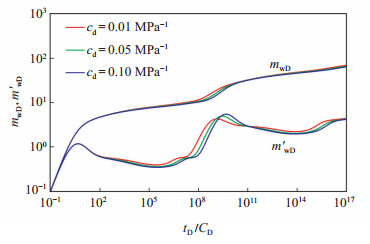
|
下载eps/tif图 图 6 解吸压缩系数对复合页岩气藏压力的影响 Fig. 6 Influence of desorption compressibility on pressure of composite shale gas reservoir |
(1)在综合考虑应力敏感效应和椭圆SRV的基础上,建立了压裂改造复合页岩气藏压力动态分析模型,并考虑了页岩气吸附解吸、Knudsen扩散、非稳态窜流和渗流等多种气体运移机制对压力的影响。
(2)采用Mathieu函数、Pedrosa变量代换、正则摄动理论、拉普拉斯变换和Stehfest数值反演法等多种方法相结合对数学模型进行求解,并绘制压力动态典型曲线,将其划分为9个流动阶段。
(3)渗透率模量的增加使得无因次曲线上移,气井生产所需压差增大;SRV半径越大,储层改造的体积越大,气井生产所需压差减小;外区裂缝渗透率的增加与流度比的减小相对应,流度比越小,外区流动所需的压降减小,显示出压裂改造对页岩气藏开发产生的良好效果;扩散系数的增加导致了页岩基质表观渗透率的增加,使得窜流系数增大;解吸压缩系数增大使得考虑解吸的储容比增大,窜流段的凹子变深且变宽。
| [1] |
张小龙, 张同伟, 李艳芳, 等. 页岩气勘探和开发进展综述. 岩性油气藏, 2013, 25(2): 116-122. ZHANG X L, ZHANG T W, LI Y F, et al. Research advance in exploration and development of shale gas. Lithologic Reservoirs, 2013, 25(2): 116-122. DOI:10.3969/j.issn.1673-8926.2013.02.021 |
| [2] |
WORRALL F, WADE A J, DAVIES R J, et al. Setting the baseline for shale gas:Establishing effective sentinels for water quality impacts of unconventional hydrocarbon development. Journal of Hydrology, 2019, 571: 516-527. DOI:10.1016/j.jhydrol.2019.01.075 |
| [3] |
李智锋, 李治平, 苗丽丽, 等. 页岩气藏纳米孔隙气体渗流特征分析. 天然气地球科学, 2013, 24(5): 1042-1047. LI Z F, LI Z P, MIAO L L, et al. Gas flow characteristics in nanoscale pores of shale gas. Natural Gas Geoscience, 2013, 24(5): 1042-1047. |
| [4] |
张烈辉, 单保强, 赵玉龙, 等. 页岩气藏表观渗透率和综合渗流模型建立. 岩性油气藏, 2017, 29(6): 108-118. ZHANG L H, SHAN B Q, ZHAO Y L, et al. Establishment of apparent permeability model and seepage flow model for shale reservoir. Lithologic Reservoirs, 2017, 29(6): 108-118. DOI:10.3969/j.issn.1673-8926.2017.06.014 |
| [5] |
王永辉, 卢拥军, 李永平, 等. 非常规储层压裂改造技术进展及应用. 石油学报, 2012, 33(增刊1): 149-158. WANG Y H, LU Y J, LI Y P, et al. Progress and application of hydraulic fracturing technology in unconventional reservoir. Acta Petrolei Sinica, 2012, 33(Suppl 1): 149-158. |
| [6] |
CLARKSON C R. Production data analysis of unconventional gas wells:Review of theory and best practices. International Journal of Coal Geology, 2013, 109/110: 101-146. DOI:10.1016/j.coal.2013.01.002 |
| [7] |
张驰. 涪陵页岩气田平桥区块深层气井压裂工艺优化与应用. 岩性油气藏, 2018, 30(6): 160-168. ZHANG C. Optimization and application of deep gas well fracturing in Pingqiao block of Fuling shale gas field. Lithologic Reservoirs, 2018, 30(6): 160-168. |
| [8] |
侯冰, 陈勉, 李志猛, 等. 页岩储集层水力裂缝网络扩展规模评价方法. 石油勘探与开发, 2014, 41(6): 763-768. HOU B, CHEN M, LI Z M, et al. Propagation area evaluation of hydraulic fracture networks in shale gas reservoirs. Petroleum Exploration and Development, 2014, 41(6): 763-768. |
| [9] |
蒋廷学, 王海涛, 卞晓冰, 等. 水平井体积压裂技术研究与应用. 岩性油气藏, 2018, 30(3): 1-11. JIANG T X, WANG H T, BIAN X B, et al. Volume fracturing technology for horizontal well and its application. Lithologic Reservoirs, 2018, 30(3): 1-11. |
| [10] |
XIE J, YANG C D, GUPTA N, et al. Integration of shale-gasproduction data and microseismic for fracture and reservoir properties with the fast marching method. SPE Journal, 2015, 20(2): 347-359. DOI:10.2118/161357-PA |
| [11] |
ZHANG Q, SU Y L, WANG W D, et al. Performance analysis of fractured wells with elliptical SRV in shale reservoirs. Journal of Natural Gas Science and Engineering, 2017, 45: 380-390. DOI:10.1016/j.jngse.2017.06.004 |
| [12] |
姜瑞忠, 滕文超, 徐建春. 压裂改造复合页岩气藏不稳定压力与产量分析方法. 天然气工业, 2015, 35(9): 42-47. JIANG R Z, TENG W C, XU J C. Transient pressure and production analysis methods for composite shale gas reservoirs stimulated by fracturing. Natural Gas Industry, 2015, 35(9): 42-47. DOI:10.3787/j.issn.1000-0976.2015.09.006 |
| [13] |
黄玲, 曾立新, 黄成惠, 等. 页岩储层敏感性特征实验研究. 天然气技术与经济, 2012, 6(5): 42-44. HUANG L, ZENG L X, HUANG C H, et al. Experimental study on fluid sensitivity of shale reservoir. Natural Gas Technology and Economy, 2012, 6(5): 42-44. |
| [14] |
尹洪军, 赵二猛, 王磊, 等. 考虑应力敏感的页岩气藏垂直裂缝井压力动态分析. 水动力学研究与进展, 2015, 30(4): 412-417. YIN H J, ZHAO E M, WANG L, et al. Pressure behavior analysis for vertical fractured well with stress sensitivity in shale gas reservoirs. Chinese Journal of Hydrodynamics, 2015, 30(4): 412-417. |
| [15] |
黄雨, 李晓平, 谭晓华. 三重介质复合气藏水平井不稳定产量递减动态分析. 天然气地球科学, 2018, 29(8): 1190-1197. HUANG Y, LI X P, TAN X H. Research on rate decline analysis for horizontal well in triple-porosity composite reservoir. Natural Gas Geoscience, 2018, 29(8): 1190-1197. |
| [16] |
DENG J, ZHU W Y, MA Q. A new seepage model for shale gas reservoir and productivity analysis of fractured well. Fuel, 2014, 124: 232-240. DOI:10.1016/j.fuel.2014.02.001 |
| [17] |
JIA Y L, FAN X Y, NIE R S, et al. Flow modeling of well test analysis for porous-vuggy carbonate reservoirs. Transport in Porous Media, 2013, 97(2): 253-279. DOI:10.1007/s11242-012-0121-y |
| [18] |
LANGMUIR I. The desorption of gases on plane surfaces of glass, mica and platinum. Journal of the American Chemical Society, 1918, 40(9): 1361-1403. DOI:10.1021/ja02242a004 |
| [19] |
郭平. 低渗透致密砂岩气藏开发机理研究. 北京: 石油工业出版社, 2009. GUO P. Research on development mechanism of low permeability tight sandstone gas reservoir. Beijing: Petroleum Industry Press, 2009. |
| [20] |
MCLACHLAN N W. Theory and application of mathieu functions. Oxford: Oxford University Press, 1951.
|
| [21] |
VAN EVERDINGEN A F, HURST W. The application of the Laplace transformation to flow problems in reservoirs. Journal of Petroleum Technology, 1949, 1(12): 305-324. DOI:10.2118/949305-G |
| [22] |
STEHFEST H. Algorithm 368:Numerical inversion of Laplace transforms. Communications of the ACM, 1970, 13(1): 47-49. |
 2019, Vol. 31
2019, Vol. 31



