脆性是岩石综合力学性质的一种表现，与岩石的矿物组成、成岩作用及应力状态等因素均有关^[1-5]。作为岩石的重要属性之一，岩石脆性对油气资源的勘探及开发起着至关重要的作用，岩石脆性评价最终可以服务于工业化压裂施工生产方案。

目前，国内外学者研究泥岩脆性参数的方法主要有矿物组分法、弹性力学参数法及应力-应变测试法^[6-12]。Jarvie等^[10]在对Barnett储层产气量较高层段的岩石样品进行研究的过程中，提出利用（石英+碳酸盐）含量/矿物总量计算其脆性指数，在此基础上张晨晨等^[13]和Cao等^[14]分别考虑样品的总有机碳（TOC）含量和镜质体反射率（R_o）对该方法进行了改进。从本质上看矿物组分法虽然可以在一定程度上表征岩石整体的脆性，然而受沉积环境等因素的影响，矿物组成相同的岩石样品其孔隙度和密度可能均不同，从而具有不同的脆性特征。一些学者提出根据对岩石样品进行的室内三轴压缩实验结果，可得到不同样品的应变强度等力学参数，从而建立应力-应变关系曲线，进而获取特征参数来评价岩石的脆性特征，然而脆性不是岩石的某种单一属性，而是一种综合的力学特征，岩石脆性也受其物质组成、结构、孔隙及流体等因素的影响^[15-19]。利用杨氏模量和泊松比表征岩石脆性的理论依据是岩石样品的应力-应变关系，即岩石在变形和破坏时存在着明显的差异，其脆性和塑性行为也可以在全应力-应变曲线上反映出来^[20-22]，因此，在岩石脆性指数评价的过程中，须综合考虑弹性模量、泊松比、应力-应变及强度等参数的影响，这样既能够反映岩石在受压时的破坏情况，又能够反映岩石破裂后维持裂缝发展的能力。

以四川盆地新场气田须家河组五段21块岩石样品的室内三轴力学实验测试为基础，分析应力-应变关系曲线中反映的岩石脆性特征，提出改进岩石脆性指数评价的方案，并针对实测样品特征建立脆性指数模型，进而对模型的可靠性进行讨论，以期更加准确地评价岩石的脆性特征。

本次实验样品共计21块（表 1），均取自四川盆地新场气田须家河组五段，对应岩性主要有黑色、灰黑色、深灰色泥岩，黑色炭质泥岩，浅灰色、灰色砂岩等，样品的TOC质量分数主要为2%~15%，R_o主要为0.5%~2.0%，孔隙度主要为1%~4%。

表 1(Table 1)

表 1 岩石样品信息 Table 1 Data of rock samples 样品编号 岩性 w（TOC）/ % Ro/% 孔隙度/% 1 黑色泥岩 4.02 1.93 2.87 2 黑色泥岩 6.95 0.97 1.66 3 深灰色泥岩 1.05 0.74 1.01 4 黑色炭质泥岩 10.03 2.01 4.22 5 黑色泥岩 13.55 2.87 5.02 6 黑色炭质泥岩 6.75 2.23 2.87 7 黑色泥岩 17.42 0.85 1.27 8 灰黑色泥岩 4.43 1.98 2.64 9 深灰色泥岩 2.01 0.92 1.29 10 黑色泥岩 6.74 1.88 3.46 11 灰色砂岩 2.46 0.48 2.32 12 浅灰色粉砂岩 2.76 0.92 3.67 13 灰色砂岩 1.16 0.77 3.24 14 灰色砂岩 2.24 0.43 2.76 15 灰色砂岩 1.03 0.45 3.94 16 灰色砂岩 2.14 0.39 2.58 17 灰色砂岩 3.35 1.18 4.01 18 灰色砂岩 2.29 1.26 3.92 19 浅灰色砂岩 2.64 1.15 3.52 20 浅灰色砂岩 5.06 0.43 6.68 21 灰色砂岩 3.64 1.76 3.04

下载CSV 表 1 岩石样品信息 Table 1 Data of rock samples

实验室岩石力学特征测试是研究岩石力学性质最直接的方法，为了全面地分析岩石脆性特征，对研究区岩石样品的物理性质、应力-应变特征及声波特征等进行了测试。应力-应变测试所采用的仪器是从美国MTS公司引进的数字伺服程控刚性实验机，该仪器可以在模拟测试地层条件下岩石静力学参数的同时进行超声波同步测试，进而获取纵横波速度；仪器的最高伺服轴压为1 000 kN，围压为140 MPa，孔压为70 MPa，环境温度为200 ℃；孔隙流体介质饱水或饱气。系统可在温度、压力（轴压、孔压及围压）变化组合条件下模拟各种地层条件，并对岩石力学参数、孔渗参数及超声波速进行同步测试。压力传感器测量误差小于1%；轴向位移传感器量程为-50~+50 mm，位移分辨精度为0.000 1 mm；超声波换能器对于直径25 mm样品频率为1 MHz。本次测试样品直径和长度分别为25 mm和50 mm。

本次实验对泥岩和砂岩样品的岩心分别进行模拟地层条件下的三轴饱水力学和声学测试。考虑样品所在区域地层有效围压约为32 MPa，分别测试围压12 MPa，22 MPa，32 MPa下泥岩和砂岩的应力-应变特征以及不同围压和轴压下泥岩和砂岩的纵横波速度，在21块样品中对1，11，12，13号样品测试了围压12 MPa下的应力-应变特征、纵横波速度和抗压强度，对2，3，4，5，14，15，16号样品测试了围压22 MPa下的应力-应变特征、纵横波速度和抗压强度，对6~10，17~21号样品测试了围压32 MPa下的应力-应变特征、纵横波速度和抗压强度，测试结果如表 2所列。

表 2(Table 2)

表 2 岩石样品脆性特征 Table 2 Brittleness characteristics of rock samples 样品编号 岩性 围压/MPa 总应变量/% 杨氏模量/GPa 纵波速度/（km·s-1） 横波速度/（km·s-1） 抗压强度/MPa 泊松比 可恢复性应变/% 1 泥岩 12 0.39 38.89 3.98 2.64 66.94 0.40 0.17 2 泥岩 22 0.42 23.98 4.92 2.80 67.58 0.32 0.28 3 泥岩 22 0.56 35.80 5.14 2.89 103.35 0.42 0.29 4 泥岩 22 0.71 13.45 4.51 2.75 51.35 0.40 0.38 5 泥岩 22 0.61 13.38 4.66 2.51 58.94 0.29 0.44 6 泥岩 32 0.55 41.01 5.30 2.96 115.36 0.40 0.28 7 泥岩 32 0.77 34.65 5.23 2.96 117.22 0.44 0.34 8 泥岩 32 0.46 20.58 4.70 2.79 51.13 0.41 0.25 9 泥岩 32 0.96 17.21 4.89 2.67 110.32 0.31 0.64 10 泥岩 32 0.74 24.04 5.12 2.90 104.87 0.24 0.44 11 砂岩 12 0.48 31.58 4.76 2.68 150.44 0.28 0.48 12 砂岩 12 0.63 24.32 4.82 2.87 139.14 0.31 0.57 13 砂岩 12 0.33 29.19 4.04 2.93 90.69 0.27 0.31 14 砂岩 22 0.63 33.26 5.24 3.08 185.96 0.21 0.56 15 砂岩 22 0.70 19.16 5.20 2.98 149.42 0.37 0.78 16 砂岩 22 0.48 48.70 5.23 3.01 141.88 0.27 0.29 17 砂岩 32 0.58 56.65 5.62 3.22 273.13 0.18 0.48 18 砂岩 32 0.63 37.66 5.34 3.04 224.90 0.23 0.60 19 砂岩 32 0.52 36.75 5.53 2.99 167.03 0.24 0.45 20 砂岩 32 0.83 28.50 5.45 3.11 180.34 0.29 0.63 21 砂岩 32 0.76 32.49 5.85 3.50 195.69 0.26 0.60

下载CSV 表 2 岩石样品脆性特征 Table 2 Brittleness characteristics of rock samples

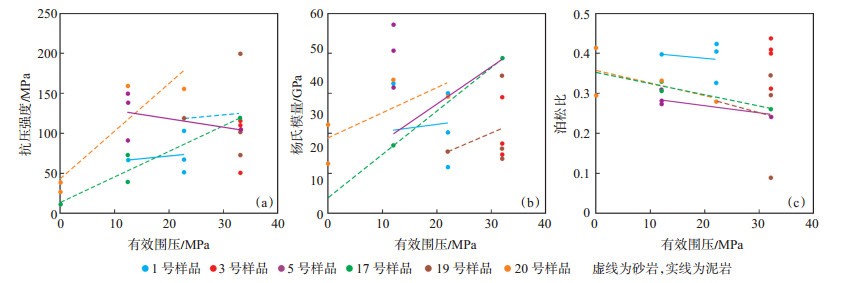
分析不同样品抗压强度、杨氏模量及泊松比与围压之间的关系表明：①岩石的抗压强度随围压的增加而增大，且砂岩的抗压强度明显高于泥岩的抗压强度；随着围压的增大抗压强度的增大量降低。当围压为0 MPa时，所选样品的抗压强度均较低；当围压从0 MPa增加到12 MPa时，所选样品的抗压强度均明显增大；当围压大于12 MPa时，随着围压的增加，大部分岩石样品抗压强度增大量变小，仅有个别样品的抗压强度增大量较大[图 1（a）]。当围压一定时，砂岩的抗压强度明显高于泥岩；围压越大，砂泥岩抗压强度在岩性上的差异越明显。②岩石的杨氏模量随围压的增加而增大，砂岩的杨氏模量高于泥岩的杨氏模量。砂泥岩的杨氏模量均随着围压的增加而增大，砂岩样品杨氏模量随围压的增加明显增大，泥岩样品的杨氏模量随围压的增加则增大量较小。在围压相同时，砂岩样品的杨氏模量高于泥岩，但是部分泥岩样品也具有较高的杨氏模量，尤其是在低围压（围压为10 MPa左右）下砂泥岩杨氏模量差异较小[图 1（b）]。③岩石的泊松比随围压的增大而减小，泥岩的泊松比大于砂岩。围压越高，岩石的泊松比越小，17，19，20号砂岩样品的泊松比随围压增加而减小的趋势较为明显，1，3，5号泥岩样品的泊松比随围压变化的趋势并不明显。在围压较低时（围压小于12 MPa），不同样品的泊松比差异并不明显，随着围压的升高，泥岩的泊松比变化不大，而砂岩的泊松比明显减小，所以在高围压下（围压大于22 MPa）泥岩的泊松比要明显高于砂岩的泊松比[图 1（c）]。

图 1

Fig. 1

下载eps/tif图 图 1 岩石抗压强度（a）、杨氏模量（b）、泊松比（c）与围压的关系 Fig. 1 Relationship of confining pressure with compressive strength (a), young's modulus (b) and Poisson's ratio (c)

目前基于应力-应变特征计算岩石样品脆性指数的方法主要有以下几种（表 3）。根据上述实验测试结果，分别利用表 3所列模型计算各个测试样品的脆性指数，以便对各个模型的评价结果进行对比和分析。

表 3(Table 3)

表 3 几种常见的基于应力-应变特征的岩石脆性指数模型 Table 3 Several brittleness index model of rocks based on stress-strain characteristics 脆性指数模型 说明 文献来源 $B_{1}=\frac{\varepsilon_{\rm{el}}}{\varepsilon_{\rm{tot}}}$ 可恢复性应变与总应变之比 Hucka等[23] $B_{2}=\frac{W_{\rm{el}}}{W_{\rm{tot}}}$ 可恢复性应变能与总应变能之比 Hucka等[23] $B_{3}=\frac{\varepsilon_{\rm{res}}-\varepsilon_{\rm{tot}}}{\varepsilon_{\rm{tot}}}$ 关于残余应变与总应变的函数 Hajiabdolmajid等[24] $B_{4}=\frac{\tau_{\max }-\tau_{\rm{res}}}{\tau_{\max }}$ 关于残余强度与峰值强度的函数 Bishopa等[25] $B_{5}=\frac{\varepsilon_{\rm{tot}}-\varepsilon_{\min }}{\varepsilon_{\max }-\varepsilon_{\min }}+\frac{\tau_{\max }-\tau_{\rm{res}}}{E_{p}\left(\varepsilon_{\rm{res}}-\varepsilon_{\rm{tot}}\right)}$ 关于峰前应变与峰后应变的函数 李庆辉等[6] $B_{6}=\frac{1}{2}\left(\frac{Y m-Y m_{\min }}{Y m_{\max }-Y m_{\min }}+\frac{\mu-\mu_{\max }}{\mu_{\min }-\mu_{\max }}\right)$ 关于杨氏模量与泊松比的函数 Grieser等[26] 注：εe1，εtot，εres分别为样品的弹性应变量、总应变量、残余应变量；We1，Wtot分别为样品的弹性应变能、总应变能；τmax，τres分别为样品的峰值强度、残余强度，MPa；εmax，εmin分别为样品总应变量的最大值、最小值；Ym为样品的杨氏模量，GPa；μ为样品的泊松比；Ymmax，Ymmin分别为样品杨氏模量的最大值、最小值，GPa；μmax，μmin分别为样品泊松比的最大值、最小值

下载CSV 表 3 几种常见的基于应力-应变特征的岩石脆性指数模型 Table 3 Several brittleness index model of rocks based on stress-strain characteristics

（1）应变和应变能

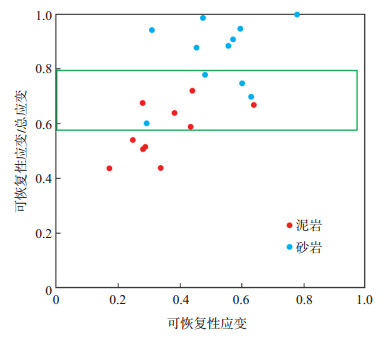
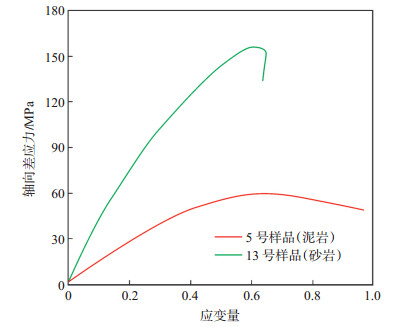
模型B₁和B₂分别用岩石可恢复应变占总应变的大小值、可恢复应变能占总应变能的大小值来评价岩石的脆性。分别计算了21块测试样品的可恢复性应变/总应变与可恢复性应变的关系（图 2）。从图 2可以看出，绿色框线内标出的部分样品具有相近的可恢复性应变/轴向总应变值。5号泥岩样品表现出典型的塑性破坏特征，13号砂岩样品表现出典型的脆性破坏特征（图 3），且可见部分高脆性砂岩样品的杨氏模量远高于低脆性的泥岩样品（参见表 2）。

图 2

Fig. 2

下载eps/tif图 图 2 砂泥岩样品的可恢复性应变/总应变与可恢复性应变的关系 Fig. 2 Relationship between the ratio of recoverable strain to total strain and recoverable strain of sand and mudstone samples

图 3

Fig. 3

下载eps/tif图 图 3 部分砂泥岩样品的轴向差应力与应变量的关系 Fig. 3 Relationship between axial differential stress and strain of some sand and mudstone samples

（2）残余强度

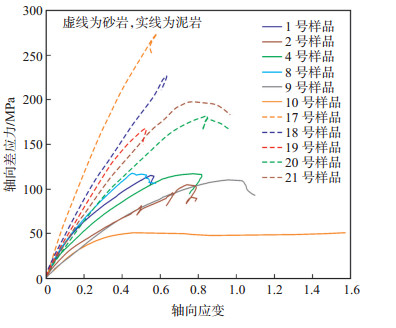
模型B₃，B₄，B₅均考虑引入或者使用残余强度评价泥岩的脆性，但是，由图 4可知，测试样品1，2，4，8的峰后曲线并未呈现出塑性破坏特征，而是表现为典型的脆性破坏特征。分析原因认为，使用模型B₃，B₄，B₅评价样品的脆性时主要是基于试样的破坏形式进行评价的，当样品表现出应变软化的变形特征，即峰后曲线斜率小于0，应变随应力的增加而降低。对于部分泥岩样品，其破坏形式为脆性断裂，因此，这些评价方法不再适用。

图 4

Fig. 4

下载eps/tif图 图 4 围压32 MPa下不同岩石样品的应力-应变曲线 Fig. 4 Stress-strain curves of different rock samples under confining pressure of 32 MPa

（3）杨氏模量和泊松比

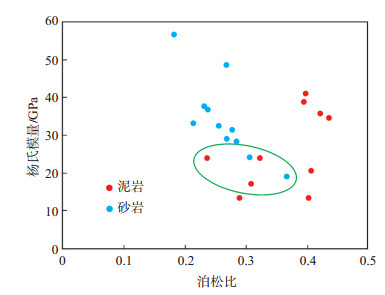
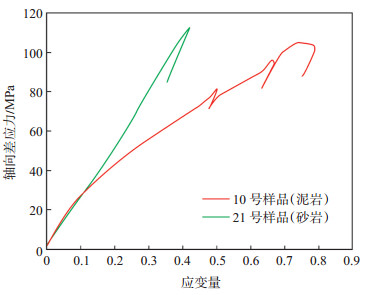
使用归一化的杨氏模量和泊松比评价岩石的脆性是现场评价岩石脆性的重要方法。部分砂岩样品与泥岩样品具有相近的抗压强度、杨氏模量和泊松比（图 5绿色圈中所示），其中10号样品的塑性应变量远高于21号样品，21号样品表现出典型的脆性破坏特征，10号样品的塑性破坏特征较为明显（图 6），可见仅使用杨氏模量和泊松比建立脆性指数，不能够较好地适应岩石的脆性特征。

图 5

Fig. 5

下载eps/tif图 图 5 砂泥岩样品杨氏模量与泊松比的关系 Fig. 5 Relationship between Young's modulus and poisson's ratio of sand and mudstone samples

图 6

Fig. 6

下载eps/tif图 图 6 部分砂泥岩样品的轴向差应力与应变量的关系 Fig. 6 Relationship between axial differential stress and strain of some sand and mudstone samples

通过分析脆性指数与应力、应变参数的关系可知，抗压强度、弹性模量及弹性应变与总应变之比越大、泊松比越小，则岩石的脆性越大。在具体区分岩石样品脆性时传统的脆性指数评价方法效果并不好，如泥岩可以有较高的杨氏模量，砂岩也可以有较低的杨氏模量和较高的泊松比。根据不同岩石样品应力-应变曲线特征参数的差异，假设高脆性岩石具有高杨氏模量、低泊松比、高可恢复性应变量与总应变量之比、高屈服强度与抗压强度之比的特征，建立这些参数与脆性指数的函数关系，并采用归一化处理方法[式（1）—（4）]计算基于杨氏模量的脆性因子（B_Ym）、基于泊松比的脆性因子（B_μ）、基于可恢复应变与总应变的脆性因子（B_Rε）、基于屈服强度与抗压强度的脆性因子（B_Rσ），建立综合脆性指数B_n [式（5）]，进而对岩石样品的脆性进行评价。

式中：${B_\varepsilon } = \frac{{{\varepsilon _{{\rm{el}}}}}}{{{\varepsilon _{{\rm{tot}}}}}}$。

式中：${B_\sigma } = \frac{{{\sigma _y}}}{{{\sigma _p}}}$，σ_y和σ_p分别为屈服强度和抗压强度，MPa。

综合脆性指数由以上4个归一化脆性因子联合组成，即

式中：α，β，γ，δ均为相关系数。

为了找出模型中可有效反映岩石脆性的脆性因子，开展如下工作：考虑到高脆性砂岩和低脆性泥岩的显著差异，假设高脆性砂岩的脆性指数为1，低脆性泥岩的脆性指数为0；对B_n与B_Rε，B_μ，B_Rσ，B_Ym的相关性分别进行了分析，结果表明B_n与B_Rε具有较好的相关性，而与B_μ，B_Rσ，B_Ym也具有一定的相关性（表 4）。多元回归显示，B_μ和B_Rσ没有显著差异（显著性> 0.05）；共线性分析显示，B_μ和B_Rσ均存在严重的共线性（表 5）。将共线性严重的影响因素排除，重新拟合。基于以上分析，认为在研究区脆性指数模型中B_μ，B_Rσ对于提高模型准确程度贡献极小，可设β，δ取值为0，用B_Rε和B_Ym来表示岩石的脆性指数。通过多元回归分析得到α，γ取值分别为0.477和0.662，即

表 4(Table 4)

表 4 综合脆性指数Bn与BYm，Bμ，BRε，BRσ的相关性分析 Table 4 Correlation analysis of comprehensive brittleness index (Bn) and BYm, Bμ, BRε, BRσ 相关类型 BYm Bμ BRε BRσ 皮尔森相关性系数 0.676** 0.526** 0.806** 0.525* 显著性（双侧） 0 0.01 0 0.010 注：样品数为21；**表示在0.01水平（双侧）上显著相关；*表示在0.05水平（双侧）上显著相关

下载CSV 表 4 综合脆性指数Bn与BYm，Bμ，BRε，BRσ的相关性分析 Table 4 Correlation analysis of comprehensive brittleness index (Bn) and BYm, Bμ, BRε, BRσ

表 5(Table 5)

表 5 回归方程中自变量的显著性分析 Table 5 Significance analysis of independent variable in regression equation 自变量 回归系数 标准差 检验值 显著性 BYm 1.300 0.256 5.073 0 Bμ -0.242 0.324 -0.746 0.465 BRε 1.543 0.215 7.189 0 BRσ -0.288 0.237 -1.216 0.240 注：当0.01 < 显著性 < 0.05，为差异显著；当显著性 < 0.01，为差异极显著

下载CSV 表 5 回归方程中自变量的显著性分析 Table 5 Significance analysis of independent variable in regression equation

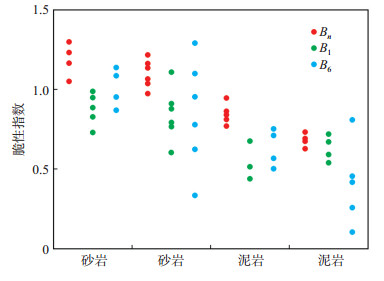
通过分析可知，高脆性砂岩的脆性明显高于低脆性泥岩的脆性，所以理想的脆性指数应该能够明显区分高脆性砂岩和低脆性泥岩。由图 7可知，B₁和B₆高脆性砂岩和低脆性泥岩脆性指数的分布区间存在重叠，不能明确对二者进行区分，而B_n高脆性砂岩和低脆性泥岩脆性指数的分布区间差异明显，可见B_n在区分岩石脆性高低上较B₁和B₆具有更好的效果。

图 7

Fig. 7

下载eps/tif图 图 7 不同岩石样品脆性指数评价 Fig. 7 Evaluation of brittleness index of different rock samples

（1）选取四川盆地新场气田须家河组五段的21块砂泥岩样品，基于不同样品对应的应力-应变曲线特征参数的差异，对比分析了现有的基于应力-应变曲线的脆性评价方法，结果表明传统的脆性指数评价方法在评价岩石脆性时效果不佳。

（2）分别计算了基于杨氏模量的脆性因子（B_Ym）、基于泊松比的脆性因子（B_μ）、基于可恢复应变与总应变的脆性因子（B_Rε）、基于屈服强度与抗压强度的脆性因子（B_Rσ），综合室内岩石力学测试结果建立了脆性指数B_n与B_Ym，B_μ，B_Rε，B_Rσ的函数关系式，并通过多元回归方法建立新的脆性指数模型，评价结果表明该脆性指数模型能够较好地区分研究区高脆性泥岩、低脆性泥岩和砂岩。