2. 中国药科大学药学院中药制剂教研室, 江苏 南京 210009
2. Department of Traditional Chinese Pharmaceutics, School of Pharmacy, China Pharmaceutical University, Nanjing 210009, China
共晶是指活性药物成分 (active pharmaceutical ingredient, API) 和共晶形成物 (cocrystal coformer, CCF) 按固定化学计量比在氢键或其他非共价键的作用下自组装形成的超分子复合物[1, 2]。在不破坏药物共价结构的前提下, 共晶的形成可改善药物的溶解度和溶出速率[3, 4], 从而提高药物的口服生物利用度[5, 6]; 此外, 共晶还可提高某些易降解药物的化学稳定性[7], 具有良好的应用前景。
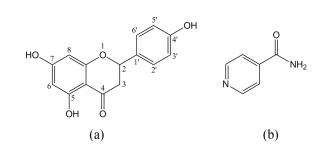
柚皮素 (4', 5, 7-三羟基二氢黄酮, NAR, 图 1a) 是柚皮苷水解一分子的葡萄糖和鼠李糖得到的苷元, 属二氢黄酮类化合物, 具有抗菌、抗炎、抗氧化、止咳祛痰、降血脂、抗肿瘤和抗粥样动脉硬化等药理作用[8-10], 被广泛地应用于医药、食品等领域。然而, 柚皮素几乎不溶于水 (46 ± 6 μg·mL-1, 298 K)[11], 口服生物利用度低 (5.81%)[12], 极大地限制了其临床应用。异烟酰胺 (INT, 图 1b) 是共晶中常用的碱性小分子配体, 具有杂环N原子结构, 易与多羟基黄酮类化合物的羟基通过氢键连接形成共晶, 如槲皮素-异烟酰胺共晶[13]、木犀草素-异烟酰胺共晶[14]和染料木素-异烟酰胺共晶[15]等。
|
Figure 1 Chemical structures of naringenin (NAR, a) and isonicotinamide (INT, b) |
共晶的热力学研究可获得API、CCF及溶剂所构成的三元体系在不同条件下最稳定的组成和状态[16, 17]。共晶形成过程中影响因素较多, 主要有化学计量比 (API/CCF)、温度和溶剂等[18]。目前, 温度及溶剂对共晶的热力学影响的研究少见报道, 本文通过测定不同温度、不同溶剂中柚皮素-异烟酰胺共晶的溶解度, 结合络合模型计算共晶的溶度积 (Ksp)、络合常数 (K12) 和反应吉布斯自由能 (ΔG) 等热力学参数, 并绘制共晶在不同温度、不同溶剂中的三元相图, 探讨温度和溶剂这两个主要因素对柚皮素-异烟酰胺共晶的热力学行为的影响, 为共晶的工业化生产提供指导。
材料与方法试剂和仪器 柚皮素 (纯度≥98.0%, 南京泽朗医药科技有限公司); 异烟酰胺 (纯度99.0%, 国药集团化学试剂有限公司); 乙醇 (分析纯, 无锡亚盛化工有限公司); 甲醇 (分析纯, 南京化学试剂有限公司); 异丙醇、乙酸乙酯 (分析纯, 江苏强盛功能化学股份有限公司); 甲醇 (色谱纯, Merck); 实验用水为Milli-Q水纯化系统 (美国Millipore公司) 制得; 其他试剂均为分析纯。RC-806智能溶出仪 (天津天大天发科技有限公司); 高效液相仪 (LC-10AD泵, SPD-10A检测器, Shimadzu, Japan); Shimadzu LC Solution色谱工作站。
柚皮素-异烟酰胺共晶的制备-混悬液结晶法 称取柚皮素1.5 g与异烟酰胺1.345 g (摩尔比为1:2) 于4个50 mL烧杯中, 分别加入30 mL甲醇、乙醇、异丙醇和乙酸乙酯, 薄膜密封后于298 K水浴中搅拌3 h, 抽滤, 所得固体产物于室温下减压干燥12 h, 即得柚皮素-异烟酰胺共晶, 置干燥器中备用。
溶出度测定 根据《中国药典》2010年版二部附录X C第二法桨法, 分别测定柚皮素、柚皮素和异烟酰胺物理混合物及柚皮素-异烟酰胺共晶在水中的溶出行为。将上述3种粉末进行过筛处理 (100目筛, 149 μm), 使样品粉末粒径均匀分布。具体溶出条件如下:溶出介质为水, 体积为900 mL, 转速50 r·min-1, 溶出温度保持在37 ℃。分别称取适量的柚皮素、柚皮素-异烟酰胺共晶及物理混合物 (相当于柚皮素4 mg), 投入溶出介质中, 分别于10、20、30、40和60 min时取溶出液5 mL, 用0.22 µm水膜过滤, 并及时补加溶出介质5 mL。续滤液采用HPLC分析测定各样品的溶出度。所有样品平行测定3次。
共晶的溶出涉及到两个过程, 溶质分子从晶格中释放出来和溶质分子的溶剂化过程[19], 也就是说共晶的溶出需要克服两方面的障碍, 晶格能和溶剂化自由能[20], 即:
| $ \Delta {{G}_{\text{solution}}}=\Delta {{G}_{\text{lattice}}}+\Delta {{G}_{\text{salvation}}} $ |
假设共晶在溶出过程中忽略溶剂化的过程, 只考虑克服晶体的晶格能, 与晶格能有关的参数有熔点 (Tm) 和熔融焓 (ΔHm), 计算T温度下 (℃) 共晶在水中的理想溶解度的摩尔分数 (Xideal), 公式如下, 结果发现实际测定的共晶在水中的溶解度远远小于理想溶解度, 这说明不能仅采用晶格能参数来预测疏水性药物共晶的溶出, 溶剂化作用是影响共晶溶出的主要因素。
| $ \ln {{X}_{\text{ideal}}}=\frac{-\Delta {{H}_{\text{m}}}}{R}\left( \frac{{{T}_{\text{m}}}-T}{{{T}_{\text{m}}}T} \right) $ |
此外, 根据Noyes-Whitney溶出方程, 药物的溶出速率 (dC/dt) 与如下因素相关:
| $ \frac{\text{d}C}{\text{d}t}=\frac{D\times S}{V\times h}\left( {{C}_{\text{s}}}-C \right) $ |
其中, D为扩散系数, S为药物表面积, V为溶出介质的体积, h为扩散层厚度, Cs为溶质在溶出介质中的溶解度 (固体表面饱和层浓度), C为t时间溶液主体中溶质的浓度。
柚皮素、异烟酰胺、柚皮素-异烟酰胺共晶溶解度的测定 分别量取5 mL不同的溶剂 (甲醇、乙醇、异丙醇、乙酸乙酯) 于洁净的西林瓶中, 分别加入过量的柚皮素、异烟酰胺、柚皮素-异烟酰胺共晶后, 密封, 置于298 K恒温振荡箱中振荡24 h。待各样品达到溶解平衡后, 0.22 μm有机微孔滤膜过滤, 续滤液经适当稀释后采用HPLC法测定溶液中柚皮素和异烟酰胺的浓度。所有样品平行测定3次。此外, 也测定了柚皮素-异烟酰胺共晶等在303 K和308 K两种温度下乙醇中的溶解度。
溶液中柚皮素和异烟酰胺浓度的测定采用HPLC法, 色谱条件为:采用Inertsil ODS C18色谱柱 (150 mm × 4.6 mm, 5 µm), 柱温25 ℃; 以甲醇-0.2%磷酸 (60:40) 为流动相, 流速为1.0 mL·min-1; 检测波长为285 nm, 灵敏度0.05 aufs; 进样体积为10 µL。在该色谱条件下, 柚皮素、异烟酰胺的保留时间分别为4.6和2.0 min; 柚皮素与异烟酰胺分别在1.2~150.6和4.8~120 μg·mL-1内线性良好 (r2 > 0.998);检测限分别为4.9和6.7 ng·mL-1; 平行测量数值的相对标准偏差 (% RSD) 在线性范围内均小于5%, 且准确度范围均在95%~105%之间, 准确度高, 重复性好。
不同浓度异烟酰胺溶液中柚皮素–异烟酰胺共晶溶解度的测定 以异烟酰胺在各种溶剂 (甲醇、乙醇、异丙醇、乙酸乙酯) 中的溶解度为上限, 配制一系列浓度的异烟酰胺有机溶液, 加入过量的柚皮素-异烟酰胺共晶, 密封后置于298 K恒温振荡箱中振荡24 h, 再静置2 h, 待体系达到溶解平衡后, 上清液用0.22 μm有机微孔滤膜过滤, 续滤液稀释后采用以上HPLC法测定溶液中柚皮素和异烟酰胺的浓度。所有样品平行测定3次。此外, 也测定了柚皮素-异烟酰胺共晶在303 K和308 K两种温度下不同浓度的异烟酰胺乙醇溶液中的溶解度。
柚皮素-异烟酰胺共晶络合参数的计算 柚皮素–异烟酰胺共晶的化学计量比为1:2, 以A代表共晶形成物异烟酰胺、B代表活性药物成分柚皮素, 柚皮素-异烟酰胺共晶则可以写成BA2。当共晶BA2溶解于溶液中时, 存在以下平衡[21, 22]:
| $ \text{B}{{\text{A}}_{2\left( \text{solid} \right)}}\overset{{{K}_{\text{SP}}}}{\longleftrightarrow}2{{\text{A}}_{\left( \text{soln} \right)}}+{{\text{B}}_{\left( \text{soln} \right)}} $ |
溶度积可以表示为Ksp = aA2aB ≈ [A]T2[B]T, 其中, Ksp为溶度积, a表示活度, [A]T和[B]T表示两种物质的摩尔浓度, 在理想的状态下, 浓度可以代替活度。T表示溶液中的总浓度。
以化学计量比为1:2的共晶, 在溶液中的络合形式可能有以下4种情况:无溶液络合、1:2溶液络合、1:1溶液络合及1:1+1:2溶液络合。
无溶液络合模型针对BA2型共晶, 存在以下平衡:
| $ \text{B}{{\text{A}}_{2\left( \text{solid} \right)}}\overset{{{K}_{\text{SP}}}}{\longleftrightarrow}2{{\text{A}}_{\left( \text{soln} \right)}}+{{\text{B}}_{\left( \text{soln} \right)}} $ |
假设柚皮素与异烟酰胺之间不存在络合现象 (即[A]T = [A], [B]T = [B]), 体系中柚皮素的浓度[B]T和异烟酰胺的浓度[A]T的关系式如下:
| $ {{\left[ \text{B} \right]}_{\text{T}}}={{K}_{\text{SP}}}/\left[ \text{A} \right]_{\text{T}}^{2} $ | (1) |
根据公式 (1), 将[B]T对1/[A]T2进行线性回归, 可以得到一条经过原点的直线, 通过这条直线的斜率可计算Ksp值。
1:2溶液络合模型对于BA2型共晶, 共晶中活性药物成分与配体之间存在1:2溶液络合作用, 则存在以下平衡:
| $ \begin{align} &\text{B}{{\text{A}}_{2\left( \text{solid} \right)}}\overset{{{K}_{\text{SP}}}}{\longleftrightarrow}2{{\text{A}}_{\left( \text{soln} \right)}}+{{\text{B}}_{\left( \text{soln} \right)}} \\ &{{\text{B}}_{\left( \text{soln} \right)}}+2{{\text{A}}_{\left( \text{soln} \right)}}\overset{{{K}_{12}}}{\longleftrightarrow}\text{B}{{\text{A}}_{2\left( \text{soln} \right)}} \\ \end{align} $ |
其中K12为络合常数, Ksp为溶度积, Ksp = [A]2[B], K12 = [BA2] / [A]2[B]
整理可得, [BA2] = KspK12
根据物质守恒原理可知:
[A]T = [A] + 2[BA2], [B]T = [B] + [BA2]
代入上式, 可得:
| $ \begin{align} &{{\left[ \text{A} \right]}_{\text{T}}}={{\left( {{K}_{\text{sp}}}/\left[ \text{B} \right] \right)}^{1/2}}+2{{K}_{\text{sp}}}{{K}_{12}} \\ &{{\left[ \text{B} \right]}_{\text{T}}}=\left[ \text{B} \right]+{{K}_{\text{sp}}}+{{K}_{12}} \\ \end{align} $ | (2) |
对公式 (2) 进项换算, 可得
| $ \left[ \text{B} \right]=\frac{{{K}_{\text{SP}}}}{{{\left( {{\left[ \text{A} \right]}_{\text{T}}}-2{{K}_{\text{SP}}}{{K}_{12}} \right)}^{2}}} $ |
推导得体系中柚皮素的浓度[B]T和异烟酰胺的浓度[A]T的关系式如下:
| $ {{\left[ \text{B} \right]}_{\text{T}}}=\frac{{{K}_{\text{SP}}}}{{{\left( {{\left[ \text{A} \right]}_{\text{T}}}-2{{K}_{\text{SP}}}{{K}_{12}} \right)}^{2}}}+{{K}_{\text{SP}}}{{K}_{12}} $ | (3) |
表达式 (3) 表明, 当共晶在溶液中发生1:2溶液络合时, 活性药物成分的浓度和共晶形成物的浓度之间呈非线性关系。
1:1溶液络合模型假如BA2共晶在溶液中溶解, 而API和CCF发生1:1溶液络合反应时, 溶液中存在以下平衡:
| $ \begin{align} &\text{B}{{\text{A}}_{2\left( \text{solid} \right)}}\overset{{{K}_{\text{SP}}}}{\longleftrightarrow}2{{\text{A}}_{\left( \text{soln} \right)}}+{{\text{B}}_{\left( \text{soln} \right)}} \\ &{{\text{A}}_{\left( \text{soln} \right)}}+{{\text{B}}_{\left( \text{soln} \right)}}\overset{{{K}_{11}}}{\longleftrightarrow}\text{A}{{\text{B}}_{2\left( \text{soln} \right)}} \\ \end{align} $ |
其中K11为络合常数, Ksp为溶度积。Ksp=[A]2[B], K11=[AB]/[A][B]
整理可得:
| $ \left[ \text{AB} \right]=\frac{{{K}_{\text{SP}}}{{K}_{\text{11}}}}{\left[ \text{A} \right]} $ |
根据物质守恒原理可知:
[A]T = [A] + [AB]
[B]T = [B] + [AB]
代入表达式, 整理可得:
| $ \left[ \text{A} \right]=\frac{{{\left[ \text{A} \right]}_{\text{T}}}+\sqrt{\left( \left[ \text{A} \right]_{\text{T}}^{2}-4{{K}_{\text{SP}}}{{K}_{\text{11}}} \right)}}{\text{2}} $ |
将上式两边同时乘以[A], 整理可得:
[A]2-[A]T[A] + KspK11 = 0
解上面的一元二次方程, 可得[A]:
| $ \left[ \text{A} \right]\text{=}\frac{{{\left[ \text{A} \right]}_{\text{T}}}\pm \sqrt{\left( \left[ \text{A} \right]_{_{\text{T}}}^{2}-4{{K}_{\text{SP}}}{{K}_{11}} \right)}}{2} $ |
经推导得体系中柚皮素的浓度[B]T和异烟酰胺的浓度[A]T的关系式如下:
| $ \begin{align} &{{\left[ \text{B} \right]}_{\text{T}}}=\frac{4{{K}_{\text{SP}}}}{2\left[ \text{A} \right]_{\text{T}}^{2}-4{{K}_{\text{SP}}}\pm 2{{\left[ \text{A} \right]}_{\text{T}}}\sqrt{\left( \left[ \text{A} \right]_{\text{T}}^{2}-4{{K}_{\text{SP}}}{{K}_{\text{11}}} \right)}}+ \\ &\ \ \ \ \ \ \ \ \ \ \frac{2{{K}_{\text{SP}}}{{K}_{\text{11}}}}{{{\left[ \text{A} \right]}_{\text{T}}}\pm \sqrt{\left( \left[ \text{A} \right]_{\text{T}}^{2}-4{{K}_{\text{SP}}}{{K}_{\text{11}}} \right)}} \\ \end{align} $ | (4) |
表达式 (4) 表明, 当共晶在溶液中发生1:1溶液络合时, 活性药物成分的浓度和共晶形成物的浓度之间呈非线性关系。
1:1+1:2溶液络合模型假如BA2共晶在溶液中同时存在1:1、1:2溶液络合, 则溶液中存在以下平衡:
| $ \begin{align} &\text{B}{{\text{A}}_{2\left( \text{solid} \right)}}\overset{{{K}_{\text{SP}}}}{\longleftrightarrow}\text{2}{{\text{A}}_{\left( \text{soln} \right)}}\text{+}{{\text{B}}_{\left( \text{soln} \right)}} \\ &{{\text{A}}_{\left( \text{soln} \right)}}\text{+}{{\text{B}}_{\left( \text{soln} \right)}}\overset{K11}{\longleftrightarrow}\text{A}{{\text{B}}_{\left( \text{soln} \right)}} \\ &\text{A}{{\text{B}}_{\left( \text{soln} \right)}}\text{+}{{\text{A}}_{\left( \text{soln} \right)}}\overset{{{K}_{12}}}{\longleftrightarrow}\text{B}{{\text{A}}_{\left( \text{soln} \right)}} \\ \end{align} $ |
其中K11、K12为络合常数, Ksp为溶度积。Ksp = [A]2[B], K11 = [AB] / [A][B], K12 = [BA2] / [AB][A]
整理可得: [BA2] = K11KspK12
根据物质守恒原理, 活性药物成分和配体在溶液中的浓度存在如下关系式:
[A]T = [A] + [AB] + 2[BA2]
[B]T = [B] + [AB] + [BA2]
代入, 可得:
| $ \begin{align} &{{\left[ \text{A} \right]}_{\text{T}}}\text{=}\left[ \text{A} \right]\text{+}\frac{{{K}_{\text{SP}}}{{K}_{11}}}{\left[ \text{A} \right]}\text{+2}{{K}_{\text{SP}}}{{K}_{11}}{{K}_{12}} \\ &{{\left[ \text{B} \right]}_{\text{T}}}\text{=}\frac{{{K}_{\text{SP}}}}{{{\left[ \text{A} \right]}^{2}}}\text{+}\frac{{{K}_{\text{SP}}}{{K}_{11}}}{\left[ \text{A} \right]}\text{+}{{K}_{\text{SP}}}{{K}_{11}}{{K}_{12}} \\ \end{align} $ |
[A]T两边同时乘以[A], 整理关系式如下:
[A]2 + (2K11K12Ksp-[A]T)[A] + K11Ksp = 0
求上述一元二次方程的解, 可得[A]:
| $ \left[ \text{A} \right]\text{=}\frac{{{\left[ \text{A} \right]}_{\text{T}}}-\text{2}{{K}_{11}}{{K}_{12}}{{K}_{\text{SP}}}\pm \sqrt{\left( {{\left( {{\left[ \text{A} \right]}_{\text{T}}}-\text{2}{{K}_{11}}{{K}_{12}}{{K}_{\text{SP}}} \right)}^{2}}-4{{K}_{11}}{{K}_{\text{SP}}} \right)}}{2} $ |
经推导得体系中柚皮素的浓度[B]T和异烟酰胺的浓度[A]T的关系式如下:
| $ \begin{align} &{{\left[ \text{B} \right]}_{\text{T}}}\text{=}\frac{4{{K}_{\text{SP}}}}{2\text{A}_{1}^{2}-\text{4}{{K}_{11}}{{K}_{\text{SP}}}\pm 2\text{A}\sqrt{\left( \text{A}_{1}^{2}-4{{K}_{11}}{{K}_{\text{SP}}} \right)}}+ \\ &\frac{2{{K}_{\text{SP}}}{{K}_{11}}}{{{\text{A}}_{1}}\pm \sqrt{\left( \text{A}_{1}^{2}-4{{K}_{11}}{{K}_{\text{SP}}} \right)}}+{{K}_{11}}{{K}_{12}}{{K}_{\text{SP}}} \\ \end{align} $ | (5) |
其中, A1 = [A]T-2K11K12Ksp
表达式 (5) 表明, 当共晶在溶液中发生1:1与1:2溶液络合时, 活性药物成分的浓度和共晶形成物的浓度之间呈非线性关系。
为了确定共晶在溶液中的络合形式, 测定了柚皮素–异烟酰胺共晶在不同温度、不同溶剂中的溶解度曲线, 并根据上述的共晶溶液络合模型对共晶的溶解度数据进行拟合, 计算共晶形成热力学参数 (Ksp、K11、K12)。
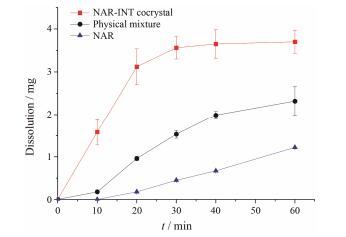
结果和讨论 1 溶出度测定柚皮素、柚皮素-异烟酰胺共晶及二者的物理混合物在水中的溶出曲线如图 2所示。由图可知, 柚皮素-异烟酰胺共晶在水中的溶出速率及溶出程度均明显高于单独柚皮素及二者的物理混合物。共晶在60 min的溶出度达到92.5%, 几乎完全溶出。
|
Figure 2 Solubility curves of NAR (▲), physical mixture (●) and NAR-INT cocrystal (■) in water at 298 K. Labeled points are measured values and lines are fitted values |
根据共晶的溶出涉及的晶格能和溶剂化自由能理论, 柚皮素-异烟酰胺共晶溶出提高可能有以下两个方面的原因: ① 观察实验过程可知, 柚皮素-异烟酰胺共晶的润湿性优于柚皮素原料药及物理混合物, 在粒径保持一致的情况下, 润湿性越好则药物的表面积越大, 从而提高共晶的溶出。② 柚皮素形成共晶后, 由于异烟酰胺的引入, 共晶的晶格能发生变化, 一定程度上影响了共晶的溶出, 主要原因可能是异烟酰胺的引入减弱了共晶中柚皮素的溶剂化障碍, 从而提高共晶的溶出。
2 不同溶剂、不同温度条件下柚皮素、异烟酰胺、柚皮素-异烟酰胺共晶的溶解度本实验考察了柚皮素、异烟酰胺、柚皮素–异烟酰胺共晶在4种不同溶剂中的溶解度, 测定结果见表 1。结果表明, 4种溶剂对柚皮素、异烟酰胺及共晶的溶解能力有较大差异, 柚皮素形成共晶后在4种有机溶剂中溶解度大小为:甲醇>乙醇>异丙醇>乙酸乙酯, 这与4种有机溶剂的极性大小顺序一致[23]。通过对共晶在3种醇类溶剂 (即甲醇、乙醇、异丙醇) 中的溶解度比较, 发现醇的碳原子数的增加, 共晶的溶解度降低, 这是因为这3种溶剂均含有极性羟基, 能与共晶组元中的部分基团形成分子间氢键, 而随着溶剂碳原子数的增加, 醇分子与共晶组元柚皮素及异烟酰胺之间形成氢键的能力减弱, 从而导致共晶的溶解度减小[24]。而与3种醇类溶剂相比, 共晶在乙酸乙酯中的溶解度最小, 这可能是因为乙酸乙酯中的C=O受到邻近氧原子的影响, 不易与共晶组元柚皮素及异烟酰胺形成分子间氢键。此外, 随着温度升高, 共晶和各组分在乙醇中的溶解度均有提高。
| Table 1 Solubility of NAR, INT and NAR-INT cocrystal in four organic solvents at different temperatures |
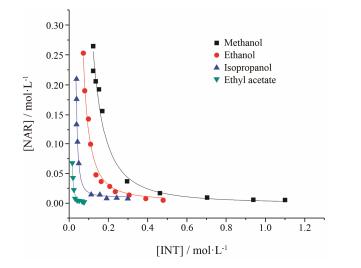
在298 K条件下, 柚皮素-异烟酰胺共晶在不同浓度异烟酰胺有机溶液中 (甲醇、乙醇、异丙醇和乙酸乙酯) 的溶解度曲线 (以异烟酰胺的总浓度为横坐标, 柚皮素的总浓度为纵坐标) 如图 3所示。由图可知, 随着异烟酰胺浓度的增加, 柚皮素的浓度呈现减小的趋势, 二者之间为非线性变化关系。
|
Figure 3 Comparison of experimental and calculated cocrystal solubility as a function of INTconcentration in methanol (■), ethanol (●), isopropanol (▲) and ethyl acetate (▼) at 298 K according to 1:2 complexation model. Labeled points are meas ured values and lines are fitted values |
首先利用1:1及1:1+1:2溶液络合数学模型对图 3中的实验数据进行拟合计算热力学参数 (Ksp、K11、K12), 然而两种络合模型中的K11均为负值 (数据未显示), 与实际情况不符, 说明共晶组元柚皮素与异烟酰胺在4种有机溶液中均不存在1:1的络合方式。
假设在有机溶液中柚皮素与异烟酰胺之间不存在络合现象, 则有:
[NAR] = Ksp / [INT]2
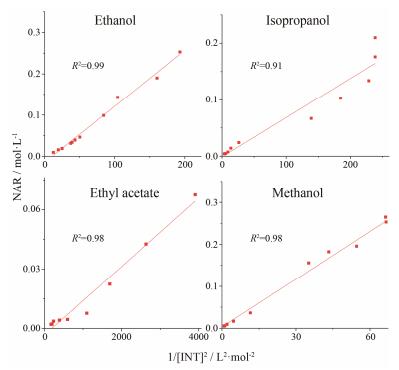
以柚皮素的浓度对异烟酰胺浓度平方的倒数进行线性回归 (图 4), 仅有甲醇体系拟合的直线应经过原点, 而其他有机溶液体系的拟合不经原点 (乙醇、乙酸乙酯) 或无线性关系 (异丙醇), 因此共晶在甲醇中可能无溶液络合现象。
|
Figure 4 The linear function between NAR and 1/[INT]2 in ethanol, isopropanol, ethyl acetate and methanol at 298 K. Labeled points are measured values and lines are fitted values |
将柚皮素-异烟酰胺共晶的溶解度数据进行1:2溶液络合模型拟合 (表 2), 发现共晶在4种溶剂中的拟合曲线和实验数据均具有较好的相关性 (R2≥0.98)。然而, 柚皮素-异烟酰胺共晶在甲醇中拟合的络合常数K12为-1.22<0, 与实际情况不符, 因此共晶组元柚皮素与异烟酰胺在甲醇中不存在1:2络合, 是以无溶液络合的形式存在; 而在其他3种溶剂 (乙醇、异丙醇和乙酸乙酯) 中以1:2络合。
| Table 2 Solubility product constant (Ksp) and complexation constant (K12) of NAR-INT cocrystals calculated according to 1:2 complexation model |
Ksp是反映共晶组元柚皮素、异烟酰胺与溶剂之间分子间作用力大小的函数, K12是反映共晶组元柚皮素与异烟酰胺之间分子间作用力大小的函数。在298 K下, 柚皮素-异烟酰胺共晶在不同有机溶剂中Ksp顺序为:甲醇>乙醇>异丙醇>乙酸乙酯 (表 2), 这与柚皮素-异烟酰胺共晶在以上溶剂中测定的溶解度一致 (表 1); 而共晶在乙酸乙酯中的络合常数K12最大, 表明共晶组元柚皮素与异烟酰胺之间的分子间作用力在乙酸乙酯中最强, 最易形成共晶。
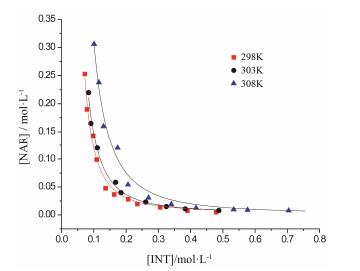
除了研究不同溶剂对柚皮素-异烟酰胺共晶络合形式的影响, 还以乙醇为模型溶剂, 研究温度对络合常数的影响。通过测定3种不同温度下柚皮素–异烟酰胺共晶在乙醇中的溶解度曲线, 并对其以1:2络合模型进行拟合 (图 5及表 2), 表明随着温度的升高, 柚皮素-异烟酰胺共晶在乙醇中Ksp随之增大, 共晶易发生解离; K12随温度的升高而减小, 与Ksp的变化趋势相反, 因此温度的升高将不利于共晶的形成。
|
Figure 5 Solubility curves of cocrystal (NAR-INT) in ethanol at different temperatures |
吉布斯自由能ΔG是判断反应自发发生的方向和限度的依据, 是评价反应体系中各组分相对稳定性的最可靠的指标。如果共晶形成方向的ΔGo < 0, 表示反应自发向共晶生成的方向移动, 该体系有利于共晶生成, 共晶是最稳定的形态; 如果共晶形成方向的ΔGo > 0, 则表明该反应体系向单组分结晶方向移动, 体系有利于单组分晶体的形成, 活性药物成分或配体较稳定[17]。
NAR和INT形成NAR-INT共晶的反应为:
NARsolid + 2INTsolid→cocrystal NAR-INTsolid (摩尔比1:2)
根据反应方程式, ΔGo存在以下关系式[25]:
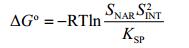
|
根据柚皮素、异烟酰胺的溶解度, 柚皮素-异烟酰胺共晶的溶度积可计算在不同温度下、不同溶剂中共晶生成反应的ΔGo, 结果如表 3所示。ΔGo均为负值, 表明在不同溶剂中 (甲醇、乙醇、异丙醇、乙酸乙酯), 反应向共晶生成的方向进行, 为自发过程。并且随温度升高, ΔGo的绝对值逐渐减小, 说明共晶生成的自发性逐渐减弱, 共晶越不容易生成。
| Table 3 Reaction Gibbs free energy (ΔGo) of cocrystal forma tion in four solvents at different temperatures |
对于非理想溶液, 物质的溶解度与温度之间符合van’t Hoff方程[26]:
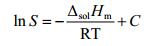
|
其中, S为摩尔溶解度值, T为溶解温度 (K), ΔsolHm为摩尔溶解焓。
将柚皮素、异烟酰胺及柚皮素-异烟酰胺共晶溶解度的自然对数对1 /T进行线性回归, 通过这些直线的斜率计算得到上述3种物质的ΔsolHm。由表 4中数据可知, 3种物质的ΔsolHm均大于0, 说明柚皮素、异烟酰胺、柚皮素-异烟酰胺共晶在乙醇中的溶解过程均为吸热过程。
| Table 4 Dissolution enthalpy (ΔsolHm) of NAR, INT and the formation of NAR-INT cocrystal in ethanol |
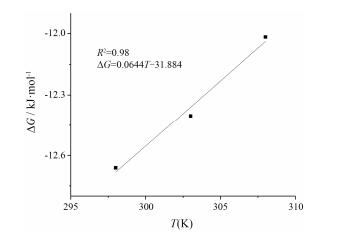
根据柚皮素-异烟酰胺共晶生成反应的ΔGo与温度之间的关系, ΔGo =ΔH-TΔS (假设共晶生成反应的反应焓值不受温度的影响), 以ΔGo对温度T进行线性回归, 如图 6所示, 由直线的斜率和截距可求出共晶生成反应的熵 (ΔS) 与反应焓 (ΔH), ΔH =-31.884 kJ·mol-1, ΔS =-0.064 4 kJ·mol-1·K, 由此可知, 柚皮素-异烟酰胺共晶的生成反应为放热反应, 当温度升高时, 共晶的生成反应速率变慢。ΔS<0表明共晶生成反应为熵减反应, 熵减放热反应可以自发进行, 但是反应的趋势会随温度的升高而减弱, 当温度升高到一定程度, 自发反应也可能无法进行, 这与上述结果一致。
|
Figure 6 The linear function between ΔG and T(K). Labeled points are measured values and lines are fitted values |
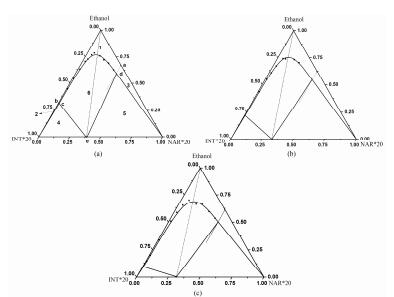
以298 K条件下乙醇中共晶的三元相图 (图 7a) 为例, 单位为各组分的摩尔分数, 点a、b分别为柚皮素、异烟酰胺在纯溶剂中的溶解度, 点e为共晶点, 点c、d为共晶的三相点, 点c表示异烟酰胺与共晶的饱和溶液体系, 点d表示柚皮素与共晶的饱和溶液体系, cd为共晶在乙醇中的溶解度曲线。区域1为柚皮素及异烟酰胺的不饱和溶液的单相区, 区域2、区域3和区域6分别表示固态异烟酰胺、固态柚皮素、固态共晶与其饱和溶液的两相平衡区, 区域4为固态异烟酰胺、固态共晶与其饱和溶液的三相平衡区, 区域5为固态柚皮素、固态共晶与其饱和溶液的三相平衡区。处于区域4的任意一点, 当体系达到平衡后, 其固相组成为异烟酰胺与共晶的混合物, 液相组成和c点的液相组成相同; 同理, 处于区域5的任意一点, 当体系达到平衡后, 其固相组成为柚皮素与共晶的混合物, 液相组成和d点的液相组成相同。
|
图 7 Ternary phase diagrams of NAR-INT cocrystals in ethanol at 298 K (a), 303 K (b) and 308 K (c) |
由图 7可知, 异烟酰胺在乙醇中的溶解度受温度的影响较柚皮素明显, 随着温度的升高, 柚皮素与异烟酰胺溶解度之间的差距变大, 共晶区域6也更加趋于不对称, 然而在不同温度下, 1:2化学计量比的直线仍然可以与共晶的溶解度曲线cd相交, 说明从柚皮素和异烟酰胺摩尔比为1:2的乙醇溶液中蒸发溶剂能够得到单一共晶。此外, 温度降低, 柚皮素及异烟酰胺不饱和溶液的单相1区变小, 表明降温有利于共晶的生成。
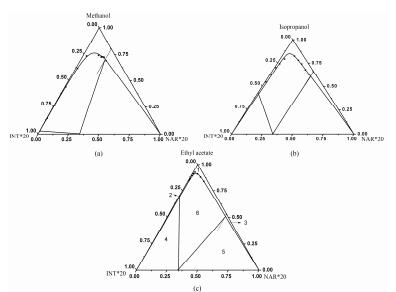
由298 K条件下共晶在4种溶剂中的三元相图 (图 7a及图 8) 可知, 乙酸乙酯相较于其他3种溶剂, 其不饱和单相区面积 (区域1) 最小, 说明乙酸乙酯中共晶最易析出。
|
Figure 8 Ternary phase diagrams of NAR-INT cocrystals in methanol (a), isopropanol (b) and ethyl acetate (c) at 298 K |
本文采用混悬液结晶法制备柚皮素-异烟酰胺共晶, 在水中的溶出曲线表明共晶的溶出行为较柚皮素及其物理混合物具有显著优势。研究其在不同溶剂和不同温度下的形成热力学, 结果表明柚皮素-异烟酰胺共晶为熵减放热的自发反应; 在乙醇、异丙醇、乙酸乙酯中属于1:2溶液络合模型, 而在甲醇中属于无溶液络合情况。结合共晶三元相图, 表明共晶在乙酸乙酯中最易形成。
| [1] | Gao Y, Zu H, Zhang JJ. Pharmaceutical cocrystals[J]. Prog Chem (化学进展), 2010, 22: 829–836. |
| [2] | Shan N, Zaworotko MJ. The role of cocrystals in pharmaceutical science[J]. Drug Discov Today, 2008, 13: 440–446. DOI:10.1016/j.drudis.2008.03.004 |
| [3] | Gao Y, Zu H, Zhang JJ. Enhanced dissolution and stability of adefovir dipivoxil by cocrystal formation[J]. J Pharm Pharmacol, 2011, 63: 483–490. DOI:10.1111/j.2042-7158.2010.01246.x |
| [4] | Huang YT, Zhang BW, Gao Y, et al. Baical-ein-nicotinamide cocrystal with enhanced solubility, dissolution, and oral bioavailability[J]. J Pharm Sci, 2014, 103: 2330–2337. DOI:10.1002/jps.24048 |
| [5] | Gao Y, Gao J, Liu Z, et al. Coformer selection based on degradation pathway of drugs:a case study of adefovir dipivoxil-saccharin and adefovir dipivoxil-nicotinamide cocrystals[J]. Int J Pharm, 2012, 438: 327–335. DOI:10.1016/j.ijpharm.2012.09.027 |
| [6] | Jung MS, Kim JS, Kim MS, et al. Bioavailability of indo-methacin-saccharin cocrystals[J]. J Pharm Pharmacol, 2010, 62: 1560–1568. DOI:10.1111/j.2042-7158.2010.01189.x |
| [7] | Swarbrick J. Encylopedia of Pharmaceutical Technology[M]. New York: Informa Healthcare USA Inc, 2007: 615-635. |
| [8] | Ribeiro IA, Rocha J, Sepodes B, et al. Effect of naringin enzymatic hydrolysis towards naringenin on the anti-inflammatory activity of both compounds[J]. J Mol Catal B, 2008, 52: 13–18. |
| [9] | Yu J, Wang L, Walzem RL, et al. Antioxidant activity of citrus limonoids, flavonoids, and coumarins[J]. J Agricul Food Chem, 2005, 53: 2009–2014. DOI:10.1021/jf0484632 |
| [10] | Liu L, Shan S, Zhang K, et al. Naringenin and hesperetin, two flavonoids derived from citrus aurantium up-regulate transcription of adiponectin[J]. Phytother Res, 2008, 22: 1400–1403. DOI:10.1002/ptr.v22:10 |
| [11] | Khan AW, Kotta S, Ansari SH, et al. Enhanced dissolution and bioavailability of grapefruit flavonoid naringenin by solid dispersion utilizing fourth generation carrier[J]. Drug Dev Ind Pharm, 2014, 41: 772–779. |
| [12] | Kanaze F, Bounartzi MM, Niopas I. Pharmacokinetics of the citrus flavanone aglycones hesperetin and naringenin after single oral administration in human subjects[J]. Eur J Clin Nutrit, 2007, 61: 472–477. |
| [13] | Smith AJ, Kavuru P, Wojtas L, et al. Cocrystals of quercetin with improved solubility and oral bioavailability[J]. Mol Pharm, 2011, 8: 1867–1876. DOI:10.1021/mp200209j |
| [14] | Sowa M, Ślepokura K, Matczak-Jon E. Cocrystals of fisetin, luteolin and genistein with pyridinecarboxamide coformers:crystal structures, analysis of intermolecular interactions, spectral and thermal characterization[J]. CrystEngComm, 2013, 15: 7696–7708. DOI:10.1039/c3ce41285g |
| [15] | Sowa M, Ślepokura K, Matczak-Jon E. A 1:2 cocrystal of genistein with isonicotinamide:crystal structure and hirshfeld surface analysis[J]. Acta Crystallogr C, 2013, 69: 1267–1272. DOI:10.1107/S0108270113029545 |
| [16] | Ma K. Progress in the research of screening technique and thermodynamics of pharmaceutical cocrystals[J]. Prog Pharm Sci (药学进展), 2010, 34: 529–534. |
| [17] | Zhang JJ, Zu H, Gao Y. Formation thermodynamics of adefovir dipivoxil-saccharin co-crystals[J]. Acta Phys Chim Sin (物理化学学报), 2011, 27: 547–552. |
| [18] | Ma K, Zhang Y, Kan H, et al. Thermodynamic and kinetic investigation on the crucial factors affecting adefovir dipivoxil-saccharin cocrystallization[J]. Pharm Res, 2014, 31: 1766–1778. DOI:10.1007/s11095-013-1281-3 |
| [19] | Maheshwari C, André V, Reddy S, et al. Tailoring aqueous solubility of a highly soluble compound via cocrystallization:effect of coformer ionization, pHmax and solute-solvent interactions[J]. CrystEngComm, 2012, 14: 4801–4811. DOI:10.1039/c2ce06615g |
| [20] | Alhalaweh A, Roy L, Rodríguez-Hornedo N, et al. pH-Dependent solubility of indomethacin-saccharin and carbamazepine-saccharin cocrystals in aqueous media[J]. Mol Pharm, 2012, 9: 2605–2612. DOI:10.1021/mp300189b |
| [21] | Nehm SJ, Rodriguez-Spong B, Rodriguez-Hornedo N. Phase solubility diagrams of cocrystals are explained by solubility product and solution complexation[J]. Crystal Growth Design, 2006, 6: 592–600. DOI:10.1021/cg0503346 |
| [22] | Hussain MA, Diluccio RC, Maurin MB. Complexation of moricizine with nicotinamide and evaluation of the complexation constants by various methods[J]. J Pharm Sci, 1993, 82: 77–79. DOI:10.1002/jps.2600820117 |
| [23] | Keraliya RA, Soni TG, Thakkar VT, et al. Effect of solvent on crystal habit and dissolution behavior of tolbutamide by initial solvent screening[J]. Dissolut Technol, 2010, 17: 16–21. DOI:10.14227/DT210314P1 |
| [24] | Xu SM. Thermodynamic and Solvent Complexation Studies of Carbamazepine-Succinic Acid Cocrystal (卡马西平-丁二酸共晶热力学研究及溶液络合机制的探索)[D]. Tianjin University, 2011. |
| [25] | Schartman RR. On the thermodynamics of cocrystal formation[J]. Int J Pharm, 2009, 365: 77–80. DOI:10.1016/j.ijpharm.2008.08.029 |
| [26] | Zhang SW, Chen JJ. Inference of Van't Hoff equation (Van't Hoff方程的推论)[J]. J Jishou Univ (Nat Sci Ed) (吉首大学学报 (自然科学版)), 1987, 2: 36–42. |
 2017, Vol. 52
2017, Vol. 52


