2. 澳门大学中华医药研究院, 澳门 999078
2. Institute of Chinese Medical Sciences, University of Macau, Macau 999078, China
对于变构调节的研究始于1954年, Novick和Szilard注意到吲哚-3-甘油磷酸合酶在加入色氨酸后被快速抑制[1]。1956年, Umbarger发现L-苏氨酸脱氨酶能够被L-亮氨酸抑制, 并且其抑制曲线呈S型而非米氏方程中的双曲线。这两起发现以及其他一些类似的发现, 在当时被称为“负反馈抑制酶(feedback inhibited enzymes或Novick-Szilard-Umbarger effect)”, 是变构调节概念的雏形[2]。研究者们曾试图用部分重叠的结合位点或竞争性抑制来解释此现象, 但均未获得满意的结果。1961年, Monod和Jacob[3]提出此类蛋白分子在空间至少存在两个不同的部位, 一个为催化部位, 一个为调节部位。某些物质可以与这种蛋白的调节部位相互作用而使蛋白分子构象发生改变, 进而影响催化部位, 改变蛋白的催化活性。这种现象被称为蛋白的变构调节或别构调节, 由此开创了一个全新的研究领域。英语组合单词“allosteric”即用于形容此类现象, 源于希腊语中“αλλο”(意为不同)和“στερεο”(意为三维或立体)。在变构调节的概念中, 如一个寡聚体亚基与其配体结合后, 影响到此寡聚体中另一亚基与同种配体结合的现象, 被称为协同效应(cooperative binding)。除了蛋白酶外, 研究表明G蛋白偶联受体(G protein-coupled receptor, GPCR)家族成员中普遍存在变构调节现象。鉴于GPCR是人类已知的最大一类受体和药物靶标, 近年来有关GPCR变构调节的研究受到许多关注并产生了多种理论模型, 用于解释GPCR变构调节机制。本文从变构调节和受体理论模型的形成开始, 介绍近年来广为应用的主要理论模型包括经典的三元复合体模型和针对GPCR二聚体提出的模型。鉴于变构调节理论仍处于不断完善过程中, 本文未能涵盖之内容, 敬请读者关注相关领域的进展。
1 变构调节理论模型的演化 1.1 早期理论研究对受体与配体间相互作用的认识可以追溯到对蛋白和酶学的早期研究, 其时多以化学反应动力学的方式看待这一问题。Klotz[4]在研究血红蛋白与氧相互作用时认为其过程可以表达为:
| $ {\rm{Hb}} + {{\rm{O}}_{\rm{2}}} \Leftrightarrow {\rm{Hb}}{{\rm{O}}_{\rm{2}}}{\rm{ }}K = \frac{{{\rm{([Hb}}{{\rm{O}}_{\rm{2}}}{\rm{])}}}}{{{\rm{([Hb][}}{{\rm{O}}_{\rm{2}}}{\rm{])}}}} $ |
根据此说法, 氧气与血红蛋白的理论结合曲线将为一类似反比例函数图像(图 1)。
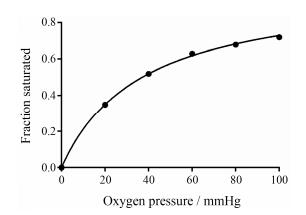 | Figure 1 Oxygen-hemoglobin theoretical binding curve according to Hüfner's theory |
20世纪初, Bohr等[5]的研究表明, 血红蛋白与氧气的结合曲线并非为一简单的反比例函数, 而是以一种S型曲线表达(图 2), 即“sigmoidal函数”。
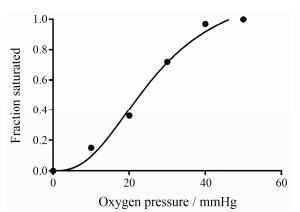 | Figure 2 Schematic representation of the oxygen-hemoglobin binding curve |
依据此现象, Hill[6]认为:一个血红蛋白能与多个氧气分子结合, 而这一结合是同时发生的, 其表达式为:
| $ {\rm{Hb}} + n{{\rm{O}}_{\rm{2}}} \Leftrightarrow {\rm{Hb(}}{{\rm{O}}_{\rm{2}}}{{\rm{)}}_n}{\rm{ }}Y = \frac{{K{{{\rm{[}}{{\rm{O}}_{\rm{2}}}{\rm{]}}}^n}}}{{{\rm{1}} + K{{{\rm{[}}{{\rm{O}}_{\rm{2}}}{\rm{]}}}^n}}} $ |
在这一理论中, n代表了与一分子血红蛋白反应的氧气分子数。尽管这一理论公式确能解释为何会出现S型曲线, 但是在进行拟合时发现n=2.5, 然而已知血红蛋白与4个氧分子结合[7], 因此这一数值不可能为1个分数。虽然有一些研究对Hill的公式进行了修改, 如Adair公式等[7], 但迟迟未能得出一种公认的且能够完全解释此现象的数学模型[8]。
1.2 MWC (Monod-Wyman-Changeux)与KNF (Koshland-Némethy-Filmer)模型1965年[9], Monod、Wyman和Changeux提出了以他们名字命名的模型(the MWC model), 这一模型及其衍生型一直沿用至今。该理论的要点为: ① 适用于寡聚体或拥有多个相同结合位点的蛋白质; ② 对于存在协同效应(或变构调节)的蛋白质而言, 其存在两种可以互相转换的构象, 即固闭的、不利于底物结合的“T”状态, 或松散的、利于底物结合的“R”状态; ③ 当蛋白/受体中的一个亚基(受到变构调节的作用)从T态转化为R态时, 其他亚基也一齐转化为R态。由于以上特点, 该模型也往往被称为“齐变模型”或“构象选择学说” (conformational selection theory)。该理论的表达如图 3所示。
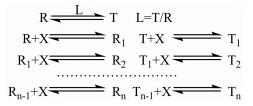 | Figure 3 Reactions of the MWC model |
图 3中第一列表示配体未加入时, 两种构象之间存在平衡, 其浓度之比为L。当加入配体后, 配体会与两种不同构象的蛋白结合。结合1分子配体后, R1和T1的解离常数分别为KR和KT。以此类推, 假设n代表一个蛋白分子最大可结合的配体数, 最后一行表达了蛋白的两种不同构象结合最多配体分子的情况。
由此可得:
① 亚基的结合率:
| $ Y = \frac{{Lca{{(1 + ca)}^{n - 1}} + a{{({\rm{1}} + a{\rm{)}}}^{n - 1}}}}{{L{{{\rm{(1}} + ca{\rm{)}}}^n} + {{{\rm{(1}} + a{\rm{)}}}^n}}} $ |
② R态蛋白的比例(由于R态更有利于结合, 故此式在某些情况下约等于上式):
| $ R = \frac{{{{({\rm{1}} + a{\rm{)}}}^n}}}{{L{{{\rm{(1}} + ca{\rm{)}}}^n} + {{{\rm{(1}} + a{\rm{)}}}^n}}} $ |
两式中a=X/KR, c=KR/KT, L=T/R, 而n代表一个蛋白分子最大可结合的配体数。
由于MWC模型(图 4)对于配体之间的正协同效应给出了充分的解释, 因此很快被应用于血红蛋白和氧的结合研究中[10]。但是此理论的缺陷在于其并不能解释负协同效应。有些研究试图对其进行修正以弥补这一缺陷, 如Li等[11]利用数学方法对其进行了改造。虽然目前尚未得到解决, 但MWC模型依然是目前应用最为广泛的变构调控理论模型, 尤其在对S型曲线图像的分析中起了相当重要的作用。
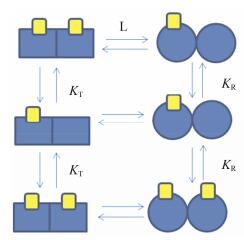 | Figure 4 Schemes of the MWC model |
MWC模型问世一年后, 出现了与之科学观点相悖的KNF模型[12], 其要点为: ① 蛋白/受体存在亲和力不同的两种状态; ② 配体与亚基的结合过程中会诱导其向高亲和力状态转化(即诱导-契合); ③ 当某一亚基转化为高亲和力状态后, 将能够诱导周围的亚基发生相同的转变。由于这些特性, KNF模型又被称为“序变模型”或“诱导-契合”模型(induced-fit model), 具体表达为:
| $ \text{R}+4\text{X}\overset{{{K}_{1}}}{\mathop{\rightleftharpoons }}\,{{\text{R}}_{1}}+3\text{X}\overset{{{K}_{2}}}{\mathop{\rightleftharpoons }}\,{{\text{R}}_{2}}+2\text{X}\overset{{{K}_{3}}}{\mathop{\rightleftharpoons }}\,{{\text{R}}_{3}}+2\text{X} $ |
上述推导过程较为简单, 对于MWC不能解释的负协同效应, 则通过调整各个不同的K值加以解决。但其中涉及的参数有K1、K2、K3和K4等, 且实际应用中可能还需要更多的参数, 因此限制了该模型的使用。此外, 关于1个亚基在转化为高亲和态后, 如何去诱导其他亚基变化, 存在多种不同的解释。尽管在实用性上可能不及MWC模型, 但KNF理论也具有相当的说服力。这两种理论之间的争论在许多方面延续至今, 甚至被MWC模型的提出者之一Changeux称为“50 years of debate”, 并将其与拉马克“用进废退”与达尔文“突变选择”之间的争议相提并论[13]。MWC及KNF模型的相关理论在解释受体的变构调节现象中都有应用。
2 G蛋白偶联受体变构调节的理论模型 2.1 G蛋白偶联受体中的变构调节现象多年研究表明, 具7次跨膜结构的G蛋白偶联受体可能存在广泛的变构调节现象。目前已有研究发现部分G蛋白偶联受体上存在“变构调节位点(allosteric site)”, 即不与内源性配体结合, 却可与变构调节剂(allosteric modulator)结合的位点。通过此过程, 变构调节剂使受体构象产生改变, 进而影响受体的其他主要配体(如乙酰胆碱之于胆碱能受体)或正位激动剂对受体的作用。目前关于GPCR变构调节的研究实例很多, 如Tan等[14]采用结构生物学手段, 证实了马拉韦罗(maraviroc)与趋化因子受体CCR5结合的变构结合位点。通过这一结合过程以及对受体构象的影响, 改变其与人类免疫缺陷病毒(human immunodeficiency virus, HIV)的结合能力, 干预病毒的入侵[15]。该药物已经于2007年在美国获批上市。Gabl等[16]发现甲酰肽受体2 (formyl peptide receptor 2, FPR2)在细胞内第三环上的肽段F2Pal16及其缩短后的产物F2Pal10, 能削弱FPR2受体被配体WKYMVm激起的钙流, 并认为其机制为F2Pal10在通过细胞膜后, 从细胞内侧对FPR2产生了变构调节。Bozinovski等[17]以IL-8的释放量作为结合量的替代, 通过Schild回归分析, 提示配体脂氧素A4 (lipoxin A4)能负性变构调节血清淀粉样蛋白(serum amyloid A)对FPR2受体的激活, 但该项研究结果尚缺乏配体结合实验数据的支持。这些研究表明, 在GPCR中变构调节极可能是一种广泛存在的现象。对GPCR变构调节的理论模型研究, 主要存在于class A类的GPCR中。此外, 对于GPCR二聚体之间互相作用的机制也已经开展了广泛的研究并提出相应的理论模型。
2.2 MWC模型与G蛋白偶联受体的变构调节MWC虽然是变构调节的一种经典模型, 但将其应用于G蛋白偶联受体中却有一定的困难。其原因之一是因为MWC模型的一大假设来源于蛋白能够形成寡聚体或拥有多个相同的结合位点, 而长期以来GPCR被认为以单体的形式存在。近年来, 这一看法虽然已随着越来越多GPCR二聚体的发现而改变, 但鲜有证据表明, 其结合过程符合MWC模型。此外, GPCR本身7次跨膜段的结构也很难容纳多个相同的结合位点。因此大多数GPCR的变构调节现象所反映的是由单个变构调节剂对正位激动剂的调节作用[18], 而非MWC模型中常见的正协同效应。其次, MWC模型主张“齐变”, 即所有结合位点都可同时转化为激活态。对于GPCR而言, 并非所有位点的状态改变都是同时且同向的[19]。GPCR的激活态可能只意味着正位位点的亲和力提高, 而变构位点的亲和力不变。
虽然受到上述因素的限制, 作者认为MWC模型对研究GPCR的变构调节仍具有很大的意义。该模型所提出的两种亲和力不同的构象(R和T态)理论被广泛地运用到各类不同的GPCR模型中。而寡聚体之间的协同效应也已经在一些GPCR的二聚体上被发现, 这些研究成果蕴含了MWC模型最基本的构想。下面将介绍一些具有实用性的GPCR理论模型。
2.3 三元复合体模型最初的三元复合体模型(ternary complex model, TCM)由De Lean等[20]在1980年提出, 用于解释配体与GPCR的结合受到G蛋白影响的现象(图 5)。这一模型简洁地阐述了GPCR的基本工作原理, 即在配体-受体-G蛋白三元复合体中, 受体的胞外部分与配体结合而胞内部分与G蛋白结合, 且任一部分都可通过对受体构象的调控而影响另一部分的结合。Ehlert[21]在1988年详细叙述了如何将此理论运用于受体的变构调节现象。该理论认为:对于一个受体而言有两个结合位点, 一个为与正位激动剂结合的正位结合位点, 另一个为与变构调节剂结合的变构位点。
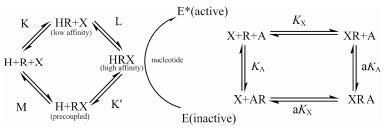 | Figure 5 The ternary complex model of GPCR function (left) and allosteric interaction (right). In the left panel, H represents ligands; R represents receptor; X represents G protein; E repre-sents response. In the right panel, X represents orthosteric ligand and A represents allosteric ligands. KX and KA are dissociation constants of A and X. This figure was prepared based on refer-ences [20] and [21] |
根据示意图, 配体的结合量可以表达为:
| $ \frac{{{\rm{[XR] + [XRA]}}}}{{{\rm{[}}{{\rm{R}}_{\rm{T}}}{\rm{]}}}} = \frac{{\frac{{{\rm{[X]}}}}{{{K_{\rm{X}}}}}{\rm{ + a}}\frac{{{\rm{[X][A]}}}}{{{K_{\rm{X}}}{K_{\rm{A}}}}}}}{{1 + {\rm{a}}\frac{{{\rm{[X][A]}}}}{{{K_{\rm{X}}}{K_{\rm{A}}}}} + \frac{{{\rm{[X]}}}}{{{K_{\rm{X}}}}}{\rm{ + }}\frac{{{\rm{[A]}}}}{{{K_{\rm{A}}}}}}} $ |
式中a代表变构调节剂加入后结合能力改变的倍数。在此模型中X代表正位激动剂, A代表变构调节剂。KX和KA代表了X和A分别单独与受体结合时的解离常数。除去各配体的解离常数外, 参数a被引入来表示变构调节的强度。当a > 1时, 表明这是一种变构增强作用; 当a < 1时, 则为变构抑制作用。需要注意的是, 在a值接近于0的情况下, A有可能成为竞争性拮抗剂[22], 因而不可盲目套用三元复合体模型。
值得注意的是, 在TCM的模型中并未引入受体存在于不同态或构象的情况, 不过De Lean等[20]关于G蛋白-受体-配体的三元复合体模型在构建时已经考虑到G蛋白偶联影响到受体亲和力的情况。据此Ehlert等[23]更倾向如下的模型(图 6)。
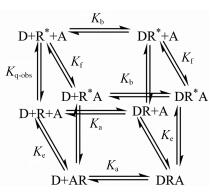 | Figure 6 The cubic ternary complex mode. D represents orthosteric ligand; R and R represents inactive/active receptor state; A represents allosteric ligand. The isomerization constant of the unoccupied receptor is described by Kq-obs. The association constants of the orthosteric (Kb and Ka) and allosteric (Kf and Ke) ligands for two states of the receptor are shown. The figure is prepared based onreference [23] |
三元复合体模型是一个简洁明了的模型, 且实验证明GPCR上的许多变构调节现象符合这一模型。如Tuček和Proška[24]总结了毒蕈碱型乙酰胆碱受体和其不同配体的相互作用, 认为其符合三元复合体模型。其后Mohr等[25]在这类受体上发现了更多类似的现象。一些毒蕈碱型受体的变构调节剂如番木鳖碱、筒箭毒碱和双复磷等被认为都结合于受体的同一个位点, 即所谓公共变构位点(common allosteric site)[26]。
随着对毒蕈碱型乙酰胆碱受体研究的深入, 通过计算机结构模拟和定点突变[27], 在毒蕈碱1型受体上发现了符合三元复合体模型的负性变构位点。而晶体结构学[28, 29]研究, 在毒蕈碱型受体1~4型亚型中均发现了与正位激动剂不同的变构位点。此外, 通过对趋化因子受体5 (CXCR5)的结构分析, 发现了HIV病毒结合位点以外的变构位点是药物马拉韦罗发挥其干预作用的药理学基础[14]。这些结构生物学研究成果证实了变构位点的存在, 以及配体-受体-变构调节剂三者之间的互相作用, 符合三元复合体模型的描述。
在其他受体方面, Koole等[30]以胰高血糖素样肽-1受体(glucagon-like peptide-1 receptor, GLP-1R)的激动剂艾塞那肽-4 (exendin-4)作为正位激动剂, 发现槲皮素(quercetin)是GLP-1R的一种符合三元复合体模型的负性变构调节剂。Wootten等[31]则依据三元复合体模型分析了大麻素受体1 (CB1 cannabinoid receptors)的多种配体, 发现其中存在变构调节现象。
2.4 多结合位点模型虽然三元复合体模型已经广泛用于分析受体上的变构调节现象, 但仍有部分实验结果不能用此模型解释。研究认为多巴胺2受体(dopamine receptor D2, D2R)[32]和腺苷1受体(adenosine A1 receptor, A1R)[33]的某些变构调节剂既能够在正位结合位点与受体结合, 又能够在变构位点调节正位激动剂(或其自身在正位点)的结合。为此设计的模型如图 7所示。
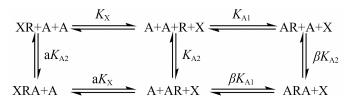 | Figure 7 A model including both allosteric modulation and competitive binding. X represents orthosteric ligand and A represents the allosteric ligands. The figure is adapted from references [22] |
其结合量可以表示为:
| $ \frac{{{\rm{[XR] + [XRA]}}}}{{{\rm{[}}{{\rm{R}}_{\rm{T}}}{\rm{]}}}} = \frac{{\frac{{\rm{X}}}{{{K_{\rm{X}}}}}{\rm{ + }}\frac{{{\rm{a[X][A]}}}}{{{K_{\rm{X}}}{K_{{\rm{A2}}}}}}}}{{\frac{{\rm{X}}}{{{K_{\rm{X}}}}}{\rm{ + 1 + }}\frac{{{\rm{a[X][A]}}}}{{{K_{\rm{X}}}{K_{{\rm{A2}}}}}} + \frac{{{\rm{[A]}}}}{{{K_{{\rm{A1}}}}}} + \frac{{{\rm{[A]}}}}{{{K_{{\rm{A2}}}}}}(1 + \beta \frac{{{\rm{[A]}}}}{{{K_{\rm{X}}}}})}} $ |
式中KA1指变构调节剂与正位结合位点的解离常数, KA2指变构调节剂与变构位点的解离常数。a为变构调节剂调节正位激动剂X结合能力的倍数, β指变构调节剂A调节另一分子A在正位结合位点结合能力的倍数。根据此公式拟合的结果如图 8所示, 左图数据为: pKX=4.6, pKA1=pKA2=4.7, a=0.25, β=27, [X]=1×10-5; 右图数据为: pKX=9, pKA1=pKA2=5, a=7, β=1, [X]=1×10-9。在图 8左半部分中, 变构调节剂之间的作用是正协同的(β > 1);而变构调节剂对X的变构调节是负性的(a < 1)。在图 8右半部分中, 变构调节剂对X的调节是正性的(a > 1);而变构调节剂在正位和变构两个不同的位点的结合则没有相互影响(β=1)。
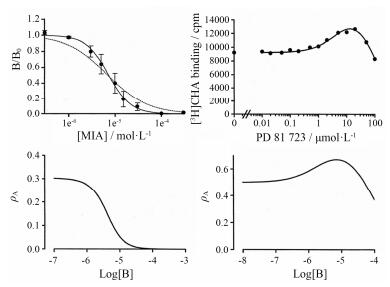 | Figure 8 Simulations to the inhibition of [3H]spiperone binding by MIA at dopamine D2 receptors (left) and the binding of the agonist, [3H]N6-cyclohexyladenosine ([3H]CHA) modulated by PD 81 723 at the A1 adenosine receptor (right). The figure was reproduced from Christopoulos & Kenakin[22] with permission |
二聚体是G蛋白偶联受体中的一种常见现象。关于二聚体与配体的结合方式有两种理论。一种认为在结合过程中, 二聚体中只有一个受体与G蛋白相连, 且连有G蛋白的受体具有较高的亲和力, 使受体易于与配体结合, 在结合过程中组成二聚体的两个受体之间并无相互作用[34]。配体与受体结合后, 藉由G蛋白的GTPase作用, 受体从高亲和力状态转回低亲和力状态。这一理论为Whorton等[35]在β2肾上腺素能受体中的实验结果所支持。另一种认为当一个配体与二聚体中的一个单元结合后, 能够变构并增强或减弱配体与二聚体中另一单元的结合作用, 这就是二聚体模型的基础理论。Albizu等[36]用荧光共振能量转移(fluorescence resonance energy transfer, FRET)方法在转染细胞和组织中都发现了催产素受体(oxytocin receptors)的二聚体, 并且发现了某些激动剂可产生负协同作用, 进一步支持上述观点。这一模型类似于MWC模型中协同作用的概念, 并且根据细节的不同分为两类(图 9和图 10)。
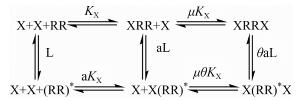 | Figure 9 Two state dimer model. X represents ligands; R represents receptor; KX represents the dissociation constants of X. The figure was prepared based on reference [37] |
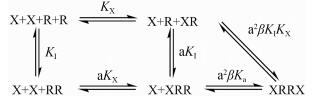 | Figure 10 The dimer model proposed by Durroux[38], including the transfer from protomer (R) to dimer (RR). X represents ligands; KX represents the dissociation constant of X; KI represents the equilibrium constant of protomer and dimer. The figure was prepared based on Durroux[38] |
其结合量可表示为:
| $ y = \frac{{{K_{\rm{X}}}(1 + {\rm{aL}})[{\rm{X}}] + 2K_{\rm{X}}^2\mu (1 + {\rm{a}}\theta {\rm{L}}){{[{\rm{X}}]}^2}}}{{1 + {\rm{L}} + {K_{\rm{X}}}(1 + {\rm{aL}})[{\rm{X}}] + 2K_{\rm{X}}^{\rm{2}}\mu (1 + {\rm{a}}\theta {\rm{L}}){{[{\rm{X}}]}^2}}} $ |
式中μ代表二聚体状态不改变的情况下对配体亲和力的影响, a、θ代表二聚体状态改变后对配体结合的影响。
两态二聚体模型(two-state dimer receptor model)[37]:此模型根据二聚体中一个单元的状态发生变化(如变为高亲和力态), 另一单元也会发生相同变化这一可能而设计。式中KX为配体的结合常数。但此模型同时也认为在低亲和力状态下的受体(RR)也存在协同作用并以μ来表示此值, 激活态(RR)下两个配体的结合常数也不一致。这些区别使得其可以解释负协同作用(通过不同a、μ、θ值), 但也增加了分析的难度。此外, 也有理论认为并非受体的构象发生了改变, 而是两个单元/原聚体(protomer)之间发生了某种交互作用(crosstalk)[38]。这一点为在腺苷A1受体二聚体中的部分发现所支持[39]。
上述模型中的结合量可表示为:
| $ {[{\rm{X}}]_{{\rm{bound}}}} = \frac{{[{\rm{R}}][{\rm{X}}]}}{{{K_{\rm{X}}}}} + \frac{{2{{[{\rm{R}}]}^2}[{\rm{X}}]}}{{{\rm{a}}{K_{\rm{X}}}{K_1}}} + \frac{{2{{[{\rm{R}}]}^2}{{[{\rm{X}}]}^2}}}{{{{\rm{a}}^2}\beta K_{\rm{X}}^2{K_1}}} $ |
式中a代表二聚体对第一分子配体结合的影响, β代表二聚体对第二分子配体结合的影响。
图 10中的模型由Durroux[38]在2005年提出, 他认为受体的单体和二聚体之间可以相互转化, 存在一种平衡。这种转化可能被配体所影响, 继而发生变构调节[40]。
综上所述, 可以发现GPCR变构调节的模型, 通常是针对配体结合实验的数据构成的。通过反应动力学中的解离常数K以及特定参数的变化, 这些模型构建了一个分析变构调节机制的系统。由此便可探知是否存在变构调节、正/负性变构调节和变构调节作用的强弱等。笔者认为目前GPCR中的变构调节模型研究大致分为两大方面:一方面, 为通过研究一个受体与不同配体之间的关系, 从中可以发现其正/负性变构调节。这为揭示受体的变构调节现象在信号通路等机制研究中的作用提供了基础。此外, 通过模型中各参数值所反映的变构调节剂的强弱, 也可以为开发变构调节药物提供一定的依据; 另一方面, 不同的理论模型是研究GPCR二聚体的一个有效手段, 通过这一方法, 将配体-受体结合实验与二聚体的形成相互联系。根据不同的假说和实验结果, 为进一步研究二聚体的形成及其对下游功能的影响提供一定的基础。
3 G蛋白偶联受体的变构调节与量效分析前述各个模型主要从配体与受体结合的亲和力(affinity)改变角度对变构调节进行分析。随着实验技术的发展和研究的深入, 研究者也希望考察变构调节现象对配体激活受体功能(efficacy)的影响。因此将变构调节的模型和配体的量效关系相互结合, 能够直观地展示不同变构调节剂对于正位激动剂产生的功能影响。通常认为, 不同激动剂通过G蛋白或β-arrestin的作用, 能够产生各种不同强度的功能。Ehlert[21]对于变构调节对受体下游的可能影响有如下阐述:
Response=f (e×[XR])
Response1=f (e×[XR]+e'×[XRA])
即认为受体下游的功能是与[XR]浓度有关的某个函数。式中e代表结合后其固有的效能参数, e'代表变构调节中三元复合物的效能参数。这一模型的内容简单, 能够用于分析部分变构调节现象中的结合数据。此外它还提供了一种模式, 在遇到不同的结合情况(如不止有一个结合位点)时, 能够通过改变上述反应路线图的方法构建不同模型, 得出符合结合数据的公式。但是, 如果需要分析受体下游的功能变化, 笔者认为这个模型显然是不够的。
最初来自许多实验数据的量效关系曲线(dose-response curve)为S型曲线, 在通常所用的分析软件中, 可提供几种与Hill公式有关的量-效关系曲线以用于分析, 如: Y=Bottom + (Top-Bottom) / (1 + 10^ ((LogEC50 -X) × HillSlope)等。这类公式往往能够较好地解释实验所得的曲线, 但其数学意义则较实际的受体结合/变构调节情况相去甚远。也有人试图以前文所述的MWC模型直接用于分析离子通道型受体的量效关系曲线, 如氯离子门控通道受体[41]。通常用于分析受体结合功能的公式有:
① Black和Leff[42]提出的“operational model”:
| $ E = \frac{{{E_{{\rm{m}}{\tau ^n}{{{\rm{[A]}}}^n}}}}}{{{{{\rm{(}}{K_{\rm{A}}} + {\rm{[A])}}}^n} + {\tau ^n}{{{\rm{[A]}}}^n}}} $ |
式中Em为所能产生的最大效能, [A]为配体的浓度, n、τ (类似于上文中所提到的e)均为参数。这一概念近来被大量运用于偏向性激动的研究中[43]。
② Melancon等[44]提出的公式:
| $ E/{E_{\rm{m}}} = \frac{{{\tau ^n}{{[{\rm{A}}]}^n}}}{{{K_{\rm{s}}}^n + {\tau ^n}{{{\rm{[A]}}}^n}}} $ |
式中Ks也为一个参数, 其他同上。当存在变构调节剂时其产生的变化见图 11。
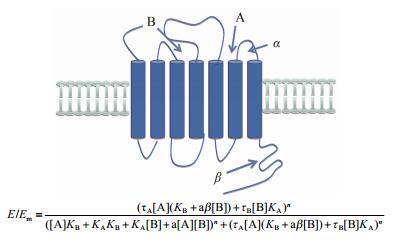 | Figure 11 Factor a describes the binding of A as modulated by allosteric ligand B; factor β describes the change of receptor function. The figure is based on Kenakin[45] |
上述两类公式都利用E/Em来反映受体的功能, 以百分比来表示这一数值, 从而避免了因使用各种不同功能单位带来的困惑, 便于进行量化分析。这一模型较全面地描述了结合过程中所产生的3种不同的配体-受体复合物(即AR、BR和ARB)及相关的效应。
Ehlert等[46]则提出了另一种观点, 他们认为受体的功能和信号转导与受体结合的G蛋白、三磷酸鸟苷(GTP)等密切相关[47], 据此提出了四元复合体模型, 其中受体(R)、G蛋白(G)和GTP (X)都存在激活态和失活态。这一模型涵盖了所有处于激活态的复合物以及能够产生下游功能的总量, 其各部分的数值将需要根据平衡常数和实验数据得出。虽然此模型过于复杂, 且实际应用过程中可能难以获得各参数的值, 但其较为全面地反映了受体及相关作用分子可能存在的各种情况。
4 结语GPCRs是已知最大的一类药物靶点。研究不同配体与对应受体的相互作用, 尤其是广泛存在的变构调节现象具有重大的生理学和药理学意义。不同理论模型有助于理解受体和配体结合的各种情况, 并可用于分析功能实验中所显示的不同效应。通过构建量化分析的模型, 将可系统地评价变构调节剂作用的机制、现象的强弱及其对受体功能的影响等, 为变构调节剂的筛选或不同内源性配体相互作用机制的研究提供支持。由于变构结合位点与生理学意义上的配体(正构)结合位点不同, 变构调节剂对于受体构象的改变往往也不同, 由此产生的药理作用机制包括偏向性激动, 为药理学研究提供了新的实验素材。同时, 对现有靶点反复进行药物筛选造成的效率下降, 可望通过变构调节位点的发现得到改善, 其效果类似于发现新的靶点。因此, 进一步发展和完善G蛋白偶联受体变构调节的理论, 具有其独特的科学价值和应用前景。
| [1] | Lindsley JE, Rutter J. Whence cometh the allosterome?[J]. Proc Natl Acad Sci U S A, 2006, 103 :10533–10535. DOI:10.1073/pnas.0604452103 |
| [2] | Changeux JP. 50 years of allosteric interactions:the twists and turns of the models[J]. Nat Rev Mol Cell Biol, 2013, 14 :819–829. |
| [3] | Monod J, Jacob F. General conclusions:teleonomic mechanisms in cellular metabolism, growth, and differentiation[J]. Cold Spring Harb Symp Quant Biol, 1961, 26 :389–401. DOI:10.1101/SQB.1961.026.01.048 |
| [4] | Klotz IM. Hemoglobin-oxygen equilibria:retrospective and phenomenological perspective[J]. Biophys Chem, 2002, 100 :123–129. DOI:10.1016/S0301-4622(02)00273-9 |
| [5] | Bohr C, Hasselbalch K, Krogh A. Ueber einen in biologischer beziehung wichtigen einfluss, den die kohlens äurespannung des blutes auf dessen sauerstoffbindung übt[J]. Skand Arch Physiol, 1904, 16 :402–412. DOI:10.1111/apha.1904.16.issue-2 |
| [6] | Hill AV. The possible effects of the aggregation of the molecules of haemoglobin on its dissociation curves[J]. J Physiol, 1910, 40 :4–7. |
| [7] | Adair GS. The hemoglobin system:VI. The oxygen dissociation curve of hemoglobin[J]. J Biol Chem, 1925, 63 :529–545. |
| [8] | Klotz IM. Ligand-receptor complexes:origin and development of the concept[J]. J Biol Chem, 2004, 279 :1–12. DOI:10.1074/jbc.X300006200 |
| [9] | Monod J, Wyman J, Changeux JP. On the nature of allosteric transitions:a plausible model[J]. J Mol Biol, 1965, 12 :88–118. DOI:10.1016/S0022-2836(65)80285-6 |
| [10] | Edelstein SJ. Extensions of the allosteric model for haemoglobin[J]. Nature, 1971, 230 :224–227. DOI:10.1038/230224a0 |
| [11] | Li QZ, Zhang LR. A new model on regulation of allosteric enzyme activity[J]. Acta Sci Natur Univ Neimongol (内蒙古大学学报:自然科学版), 1999, 30 :592–596. |
| [12] | Koshland DE Jr. Enzyme flexibility and enzyme action[J]. J Cell Comp Physiol, 1959, 54 :245–258. DOI:10.1002/(ISSN)1553-0809 |
| [13] | Changeux JP, Edelstein S. Conformational selection or induced fit? 50 years of debate resolved[J]. F1000 Biol Rep, 2011, 3 :19. |
| [14] | Tan QX, Zhu Y, Li J, et al. Structure of the CCR5 chemokine receptor-HIV entry inhibitor maraviroc complex[J]. Science, 2013, 341 :1387–1390. DOI:10.1126/science.1241475 |
| [15] | Guo ZR. First drug to inhibit HIV-1 virus invasion, Maraviroc[J]. Acta Pharm Sin (药学学报), 2016, 51 :839–842. |
| [16] | Gabl M, Winther M, Skovbakke SL, et al. A pepducin derived from the third intracellular loop of FPR2 is a partial agonist for direct activation of this receptor in neutrophils but a full agonist for cross-talk triggered reactivation of FPR2[J]. PLoS One, 2014, 9 :e109516. DOI:10.1371/journal.pone.0109516 |
| [17] | Bozinovski S, Uddin M, Vlahos R, et al. Serum amyloid A opposes lipoxin A4 to mediate glucocorticoid refractory lung inflammation in chronic obstructive pulmonary disease[J]. Proc Natl Acad Sci U S A, 2012, 109 :935–940. DOI:10.1073/pnas.1109382109 |
| [18] | May LT, Leach K, Sexton PM, et al. Allosteric modulation of G protein-coupled receptors[J]. Annu Rev Pharmacol Toxicol, 2007, 47 :1–51. |
| [19] | Canals M, Sexton PM, Christopoulos A. Allostery in GPCRs:'MWC' revisited[J]. Trends Biochem Sci, 2011, 36 :663–672. DOI:10.1016/j.tibs.2011.08.005 |
| [20] | De Lean A, Stadel JM, Lefkowitz RJ. A ternary complex model explains the agonist-specific binding properties of the adenylate cyclase-coupled beta-adrenergic receptor[J]. J Biol Chem, 1980, 255 :7108–7117. |
| [21] | Ehlert FJ. Estimation of the affinities of allosteric ligands using radioligand binding and pharmacological null methods[J]. Mol Pharmacol, 1988, 33 :187–194. |
| [22] | Christopoulos A, Kenakin T. G protein-coupled receptor allosterism and complexing[J]. Pharmacol Rev, 2002, 54 :323–374. DOI:10.1124/pr.54.2.323 |
| [23] | Ehlert FJ, Griffin MT. Estimation of ligand affinity constants for receptor states in functional studies involving the allosteric modulation of G protein-coupled receptors:implications for ligand bias[J]. J Pharmacol Toxicol Methods, 2014, 69 :253–279. DOI:10.1016/j.vascn.2014.01.002 |
| [24] | Tuček S, Proška J. Allosteric modulation of muscarinic acetylcholine receptors[J]. Trends Pharmacol Sci, 1995, 16 :205–212. DOI:10.1016/S0165-6147(00)89023-9 |
| [25] | Mohr K, Tränkle C. Allosteric effects of the alkane-bisammonium compound W84 and of tacrine on[J]. Pharmacol Toxicol, 1994, 75 :391–394. DOI:10.1111/bcpt.1994.75.issue-6 |
| [26] | Tränkle C, Weyand O, Voigtländer U, et al. Interactions of orthosteric and allosteric ligands with[J]. Mol Pharmacol, 2003, 64 :180–190. DOI:10.1124/mol.64.1.180 |
| [27] | Abdul-Ridha A, Lane JR, Mistry SN, et al. Mechanistic insights into allosteric structure-function relationships at the M1 muscarinic acetylcholine receptor[J]. J Biol Chem, 2014, 289 :33701–33711. DOI:10.1074/jbc.M114.604967 |
| [28] | Kruse AC, Ring AM, Manglik A, et al. Activation and allosteric modulation of a muscarinic acetylcholine receptor[J]. Nature, 2013, 504 :101–106. DOI:10.1038/nature12735 |
| [29] | Thal DM, Sun B, Feng D, et al. Crystal structures of the M1 and M4 muscarinic acetylcholine receptors[J]. Nature, 2016, 531 :335–340. DOI:10.1038/nature17188 |
| [30] | Koole C, Wootten D, Simms J, et al. Allosteric ligands of the glucagon-like peptide 1 receptor (GLP-1R) differentially modulate endogenous and exogenous peptide responses in a pathway-selective manner:implications for drug screening[J]. Mol Pharmacol, 2010, 78 :456–465. DOI:10.1124/mol.110.065664 |
| [31] | Wootten D, Savage EE, Willard FS, et al. Differential activation and modulation of the glucagon-like peptide-1 receptor by small molecule ligands[J]. Mol Pharmacol, 2013, 83 :822–834. DOI:10.1124/mol.112.084525 |
| [32] | Hoare SR, Strange PG. Regulation of D2 dopamine receptors by amiloride and amiloride analogs[J]. Mol Pharmacol, 1996, 50 :1295–1308. |
| [33] | Bruns RF, Fergus JH. Allosteric enhancement of adenosine A1 receptor binding and function by 2-amino-3-benzoylthiophenes[J]. Mol Pharmacol, 1990, 38 :939–949. |
| [34] | Ferré S, Casadó V, Devi LA, et al. G protein-coupled receptor oligomerization revisited:functional and pharmacological perspectives[J]. Pharmacol Rev, 2014, 66 :413–434. DOI:10.1124/pr.113.008052 |
| [35] | Whorton MR, Bokoch MP, Rasmussen SGF, et al. A monomeric G protein-coupled receptor isolated in a highdensity lipoprotein particle efficiently activates its G protein[J]. Proc Natl Acad Sci U S A, 2007, 104 :7682–7687. DOI:10.1073/pnas.0611448104 |
| [36] | Albizu L, Cottet M, Kralikova M, et al. Time-resolved FRET between GPCR ligands reveals oligomers in native tissues[J]. Nat Chem Biol, 2010, 6 :587–594. DOI:10.1038/nchembio.396 |
| [37] | Casadó V, Cortés A, Ciruela F, et al. Old and new ways to calculate the affinity of agonists and antagonists interacting with G-protein-coupled monomeric and dimeric receptors:the receptor-dimer cooperativity index[J]. Pharmacol Ther, 2007, 116 :343–354. DOI:10.1016/j.pharmthera.2007.05.010 |
| [38] | Durroux T. Principles:a model for the allosteric interactions between ligand binding sites within a dimeric GPCR[J]. Trends Pharmacol Sci, 2005, 26 :376–384. DOI:10.1016/j.tips.2005.05.006 |
| [39] | Gracia E, Moreno E, Cortés A, et al. Homodimerization of adenosine A1 receptors in brain cortex explains the biphasic effects of caffeine[J]. Neuropharmacology, 2013, 71 :56–69. DOI:10.1016/j.neuropharm.2013.03.005 |
| [40] | Gomes I, Jordan BA, Gupta A, et al. G protein coupled receptor dimerization:implications in modulating receptor function[J]. J Mol Med, 2001, 79 :226–242. DOI:10.1007/s001090100219 |
| [41] | Iwai T, Kihara H, Imaiand K, et al. Dose-response curve for anaesthetics based on the Monod-Wyman-Changeux model[J]. Br J Anaesth, 1996, 77 :517–521. DOI:10.1093/bja/77.4.517 |
| [42] | Black JW, Leff P. Operational models of pharmacological agonism[J]. Proc Roy Soc B Biol Sci, 1983, 220 :141–162. DOI:10.1098/rspb.1983.0093 |
| [43] | Kenakin T. Theoretical aspects of GPCR-ligand complex pharmacology[J]. Chem Rev, 2016 . DOI:10.1021/acs.chemrev.5600561 |
| [44] | Melancon BJ, Hopkins CR, Wood MR, et al. Allosteric modulation of seven transmembrane spanning receptors:theory, practice, and opportunities for central nervous system drug discovery[J]. J Med Chem, 2012, 55 :1445–1464. DOI:10.1021/jm201139r |
| [45] | Kenakin T. New concepts in pharmacological efficacy at 7TM receptors:IUPHAR review 2[J]. Br J Pharmacol, 2013, 168 :554–575. DOI:10.1111/j.1476-5381.2012.02223.x |
| [46] | Ehlert FJ. On the analysis of ligand-directed signaling at G protein-coupled receptors[J]. Naunyn Schmiedebergs Arch Pharmacol, 2008, 377 :549–577. DOI:10.1007/s00210-008-0260-4 |
| [47] | Kenakin T. Functional selectivity and biased receptor signaling[J]. J Pharmacol Exp Ther, 2011, 336 :296–302. DOI:10.1124/jpet.110.173948 |
 2016, Vol. 51
2016, Vol. 51


