固体药物的溶解度在制药行业中起着重要作用,常常会直接影响到药物的生物活性,溶解度数据可以为药物制剂的配伍变化研究提供一定的理论依据,并作为筛选新药的标准^[1],有助于解决药物研究和生产过程中的许多问题。

目前,测定溶解度的方法主要有通过配制饱和溶液,利用不同的分析手段分析体系固液平衡后上清液组成的平衡法^{[2, 3]},以及在预先精确称量样品中溶质和溶剂的条件下,不断改变温度或加入定量的溶质或溶剂,观察体系中固体的产生或消失来确定溶解度的动态法^{[4, 5]}等。平衡法因其设备简单、易操作、对体系平衡速率没有限制,是较常用的溶解度测定方法。然而该方法耗时长^[6],在高温或一定压力下取样困难,对不同药物需采用特定的分析手段,如化学滴定法、分光光度法^[7]和HPLC法等,故当测定药物种类较多、数量较少时,会造成分析方法各异,操作繁琐,资源浪费,为实际的科研工作带来不便。动态法通常由组合的激光监测系统代替人眼观察固体的溶解状况,并判断测定终点,平衡时间相对较短,不易达到真正的平衡,需要加强搅拌,严格控制升温速度。对于溶解过程缓慢的药物,不易使用此法。

针对上述方法的局限性,作者提出了一种对大多数药物普遍适用的溶解度测定方法。采用湿度传感器直接测定与药物饱和溶液呈平衡的空气的相对湿度^[8],避免了平衡法中对饱和溶液的取样分析过程,大大简化了测定步骤。作者用空气湿度法测定了NaCl在20～50 ℃内的溶解度,并与重量分析法及文献报道值进行了比较。

根据物理化学基本原理,与溶液呈平衡的空气的相对湿度 (H_r) 即为溶液中水的活度 (${\alpha _{{H_2}O}}$)^[8-10]。${\alpha _{{H_2}O}}$可表达为水的摩尔分数 (${x_{{H_2}O}}$) 与水的活度系数 (${\gamma _{{H_2}O}}$) 的乘积:

故可得:

其中,${\gamma _{{H_2}O}}$可由活度系数模型拟合得出。故由式 (2) 可见,若能测出空气H_r值,则可计算得出水的摩尔分数,从而求得溶质的溶解度。

目前有多种物理化学理论模型可用于计算${\alpha _{{H_2}O}}$。Sadeghi等^[11]从局部组成模型推衍得到Extended- NRTL模型,该模型考虑了溶液中各质点分子之间的相互作用,与实际溶液较为接近。作者采用此模型计算了不同温度下NaCl饱和溶液中${\alpha _{{H_2}O}}$,并由此计算了NaCl的溶解度。

在Extended-NRTL模型中,${\gamma _{{H_2}O}}$由其长程静电作用项 ($\gamma _{_{{H_2}O}}^{LR}$) 和短程非静电作用项 ($\gamma _{_{{H_2}O}}^{SR}$) 组成:

在水溶液中,$\gamma _{_{{H_2}O}}^{LR}$和$\gamma _{_{{H_2}O}}^{SR}$可分别表达为:

式中,${I_x} = {1 \over 2}\left( {z_ + ^2{x_ + } + z_ - ^2{x_ - }} \right)$是以摩尔分数表达的离子强度,其中x₊、x₋和z₊、z₋分别为正、负离子的摩尔分数和离子电荷数。上述模型方程虽然看似繁杂,但却仅包含温度、摩尔分数等简单参数^[12],实际计算过程较为简便。作者采用Excel模拟分析规划求解处理数据,在已知H_r值后通过逆运算求得${{x_{{H_2}O}}}$,进而得出溶质的溶解度。

仪器与试剂 Rotronic湿度计 (HydroPalm Hp22),探头型号: HygroClip HC2-S。相对湿度和温度的测 定范围分别为0～1和−50～100 ℃; 准确度分别为 ± 0.008和 ± 0.1 ℃,输出结果的时间间隔为1 s。FA2004型分析天平 (上海良平仪器仪表有限公司)。SDH401型恒温恒湿箱 (重庆试验设备厂)。NaCl为分析纯 (≥99.5 %,天津市瑞金特化学品有限公司)。

空气湿度法测定溶解度 取一定量的NaCl于锥形瓶中,加水,搅拌,使成饱和溶液。密闭插入湿度传感器于锥形瓶上方的空间 (图 1)。在测定温度下恒温2 h后,读取相对湿度值,根据式 (2)～(5) 计算溶解度值。

Figure 1

Figure 1

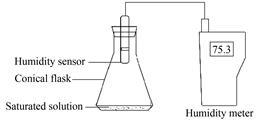
Figure 1 Assembly used in the determination of the relative air humidity in equilibrium with the solution

重量法测定溶解度 取上述已达固液平衡的NaCl饱和溶液适量,精密称定,在105 ℃下烘干至恒重后,再精密称定残留的溶质质量,计算出NaCl的溶解度^[13]。

用空气湿度法和重量法测定的溶解度值及文 献^[14]报道的溶解度值见表 1和图 2,结果表明三者基本一致。

表1(Table 1)

Table 1 Solubility of NaCl determined by air humidity solubility assay,gravimetry and reported by literature within the temperature range 20−50 ℃. n = 3,x± s T/℃ Solubility (g/100 g H2O) Air humidity solubility assay Gravimetry Literature date[14] 20 35.6 ± 0.008 36.03 ± 0.001 36 25 35.7 ± 0.007 36.12 ± 0.001 30 36.0 ± 0.015 36.24 ± 0.002 36.3 35 36.2 ± 0.006 36.50 ± 0.000 40 36.4 ± 0.019 36.57 ± 0.002 36.6 45 36.7 ± 0.024 36.74 ± 0.003 50 36.8 ± 0.016 36.95 ± 0.001 37

Table 1 Solubility of NaCl determined by air humidity solubility assay,gravimetry and reported by literature within the temperature range 20−50 ℃. n = 3,x± s

Figure 2

Figure 2

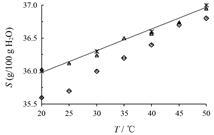
Figure 2 Comparison of NaCl solubility (S) determined by air humidity solubility assay (◇),gravimetriy (△) and reported by literature (错误！未指定书签。错误！未指定书签。) within the temperature range 20−50 ℃. n = 3,x± s

为了解相对湿度测定值对溶解度计算值的影响,进行误差分析。以25 ℃时NaCl饱和溶液的相对湿度值0.754为例,用空气湿度法测得的溶解度为35.70 g/ 100 g H₂O,若湿度测定值因误差而增加至0.764 (ΔH_r = 0.01),则溶解度的计算值将减少为34.51 g/100 g H₂O,由此得相对湿度测定误差 (DH_r) 对溶解度计算值误差 (DS) 的影响为${{\Delta S} \over {\Delta {H_r}}} = {{ - 1.19g/100g} \over {0.01}} = - 1.19$。并计算在20～50 ℃ (H_r 0.746～0.755) 内的${{\Delta S} \over {\Delta {H_r}}}$值,结果见图 3。

Figure 3

Figure 3

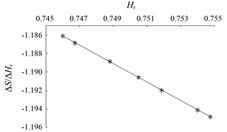
Figure 3 The impact of relative humidity (Hr) measurement error (ΔHr) on the calculated value for solubility (ΔS)

本实验中使用的湿度计用标准溶液标定后,在相对湿度0～1内湿度测定的绝对误差≤0.008,由此造成的溶解度计算值的绝对误差≤0.85 g/100 g H₂O,相对误差≤2%。

在本实验中,空气湿度法测定的相对误差≤2%,虽然其准确度不及重量分析法,但操作简便、条件易控,对大多数药物普遍适用,弥补了现有的溶解度测定方法的局限性。

众所周知,高分子化合物由于黏度很大且难以结晶,又缺乏简便易行的含量分析方法,其溶解度是很难测定的。目前常用极性相似的原则^[15]或通过比较高分子化合物与溶剂的“溶度参数”^[16]来判断其溶解的难易程度。而作者提出的新方法只需测定在平衡条件下的空气相对湿度,避免了上述困难,因而具有潜在的测定高分子化合物溶解度的能力。在后续研究工作中,将对此进行验证。