2. 西北大学 化学工程学院, 陕西 西安 710069
2. School of Chemical Engineering, Northwest University, Xi'an 710069, China
纳米药物的表面zeta电位、尺度及形状等因素对药物在体内的分布、吸收和代谢等有至关重要的影响[1, 2],因此深入分析纳米药物的特征因素对其吸收和代谢等影响的规律,对提高药物疗效、降低毒副作用及纳米药物的优化设计等具有非常重要意义。
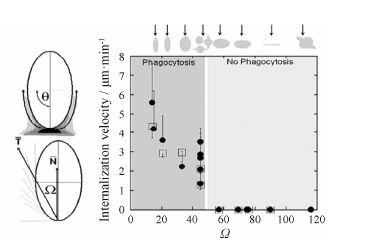
杨艳芳等[3]论述了脂质体的表面电荷和粒径对其与细胞结合和被细胞摄取的影响,分析了表面电荷和粒径对脂质体在血液、肝、脾及肿瘤组织中的吸收过程和分布情况。说明表面电荷和粒径是影响脂质体在体内被动靶向作用的重要理化因素。Champion等[4, 5]采用具有不同尺寸和形状的聚苯乙烯粒子与肺泡巨噬细胞的相互作用过程来研究吞噬现象。发现 颗粒的形状在细胞吞噬中起更主要的作用。作者设计并制得形状包括球体、扁平和扁长的椭球体、椭圆和矩形盘等药物颗粒,研究其与巨噬细胞的相互作用,并观察其随时间的变化[4, 5]。极为重要的是,引入一个无量纲形状因子 (Ω,图 1) 来表征吞噬作用和内化的速度随粒子Ω的变化关系。分析表明,在Ω ≤ 45°时,粒子很容易被内化; 在Ω > 45°时,内化现象不会发生[4, 5]。
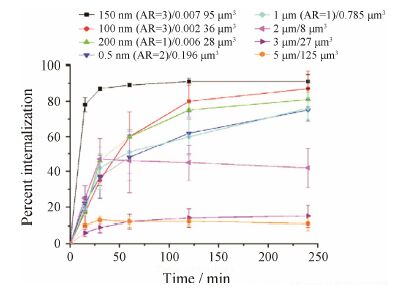
Gratton等[2, 6, 7]研究也表明,颗粒表面电荷、形状和尺寸等对吞噬细胞内化产生很大的影响,并设计制备一系列具有不同尺寸和形状的阳离子交联水凝胶,研究其与HeLa细胞的作用[6]。作者用PRINT技术 制备了一系列立方体和圆柱体,高宽比用AR (aspect ratio) 表示。结果表明,形状、尺度和体积均有影响,结果见图 2。
|
Figure 2 Internalization profiles of cylindrical and cubic-shaped PRINT particles of various sizes in HeLa cells over a 4 h incubation period at 37 ℃[2, 6]. AR: Aspect ratio |
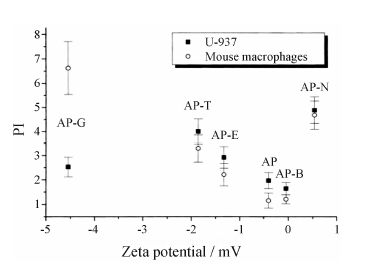
Roser等[8]引入了zeta电位描述表面改性状况,图 3给出噬菌细胞参数随zeta电位的变化。药物表面所带正负电荷不同,其表面物理化学性质不同,与吞噬细胞的作用也不同[8, 9, 10, 11, 12]。高的正负zeta电位值,相对于表面较多的正负电荷,使得药物较易和细胞发生静电相互吸引,因而具有较强的吞噬作用; 而zeta电位小甚至接近于零时,吞噬作用有所降低。
|
Figure 3 Correlation between phagocytic index and zeta potential[8] |
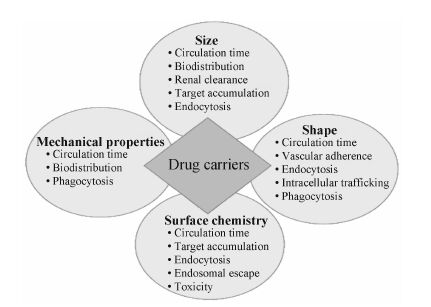
综上所述,纳米药物的化学组成、表面物理化学性质、形状和尺度大小等都会对药物在体内的分布、吸收及代谢等产生很大的影响。有学者[1]将这些作用关系形象地归纳为图 4。但是,目前纳米化药物有关表面物理化学性质、形状、尺度大小及柔韧性的合理匹配问题,还没有较为有效的评估方法。
|
Figure 4 Role of key carrier properties in drug delivery[1] |
邓聚龙等[13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23]于1980年提出的灰色理论是新兴边缘学科,该理论以“部分信息已知,部分信息未知”的“小样本”、“贫信息”不确定性系统为研究对象,主要通过对部分已知信息的生成和开发,提取有价值的信息,实现对系统运行行为、演化规律的正确描述和有效监控。
虽然已经发现纳米药物的表面zeta电位、形状和尺度大小对药物在体内的分布、吸收及代谢等有很重要的影响,但这些因素中哪个是主要因素,哪个是次要因素,哪个因素对药物吸收作用影响大,哪个因素对系统发展起推动作用需首先保证,哪个因素对系统发展起阻碍作用需加以抑制,这些问题仍未解决。本文拟通过灰色关联来分析和认识这些问题,以期为纳米药物的研发提供有益的支持。
1 纳米药物的灰色关联度分析 1.1 有关参量之间的对应关系灰色关联分析的基本思想是根据序列曲线几何形状的相似程度来判断其联系是否紧密[22, 23]。曲线越接近,相应序列之间关联度就越大,反之就越小。对一个抽象的系统或现象进行分析,首先要选准反映系统行为特征的数据序列,这被称为系统行为的映射量,用映射量来间接地表征系统行为。如用内化速率来衡量不同形状粒子进入细胞的快慢,用内化百分比来衡量不同尺寸的颗粒进入细胞的量,用zeta电位来衡量药物表面不同物理化学状态,不同电位颗粒进入细胞的多少用内化指数来表达。有了系统行为特征数据,即可做出各个序列的图形,从直观上进行分析。
从图 1可以得到颗粒形状因子Ω与相应内化速率值的对应关系数据; 从图 2可得到在4 h时不同 颗粒尺寸的内化百分数值; 从图 3得到不同电位值U-937细胞的内化指数值。
1.2 纳米药物灰色关联度的计算内化速率、内化百分数和内化指数都是药物进入细胞状态的描述,属于同一类终量,而zeta电位、Ω值和颗粒大小表述的分别是颗粒的表面性质、形状和大小。
根据灰色理论的处理方法[22, 23],可以将分别从图 1,图 2,图 3取得的数据写为如下数组,
y1 = {1.2,2.2,3.4,4.0,5.5},x1 = {45,34,22,16,14}
y2 = {83,85,80,72,70},x2 = {100,150,200,500,1 000}
y3 = {1.5,1.8,3.0,4.0,2.5},x3 ={−0.1,−0.4,−1.3,−1.9,−4.5}
按照灰色理论处理方法[22, 23],可以根据以上3组数据求出灰色关联度。
1.2.1 纳米药物的广义灰色绝对关联度计算① 对各行为序列求始点零化像
y10= {0,1.0,2.2,2.8,4.3},x10= {0,−11,−23,−29,−31}
y20= {0,2,−3,−11,−13},x20= {0,50,100,400,900}
y30= {0,0.3,1.5,2.5,3.5},x30= {0,−0.3,−1.2,−1.8,−4.4}
②求|YS1|、|XS1|、|XS1−YS1|
③计算灰色绝对关联度
同理可以计算出其余广义灰色绝对关联度
ε11 = 0.502 9 ε12 = 0.509 0 ε13 = 0.517 1
ε21 = 0.620 3 ε22 = 0.500 2 ε23 = 0.657 9
ε31 = 0.503 0 ε32 = 0.502 6 ε33 = 0.523 1
得到绝对关联矩阵
① 求特征行为序列和相关因素行为序列的初值像
${Y_1}^\prime$= (1,1.83,2.83,3.33,4.58),
${X_1}^\prime$= (1,0.76,0.49,0.36,0.31)
=${Y_2}^\prime $(1,1.02,0.96,0.87,0.84),= (1,1.5,2,5,10)
=${Y_3}^\prime$(1,1.2,2,2.67,1.67),= (1,4,13,19,45)
②${Y_i}^\prime$和${X_j}^\prime$的始点零化像分别为
${Y_1}{\prime ^0}$= (0,0.83,1.83,2.33,3.58),
${X_1}{\prime ^0}$= (0,−0.24,−0.51,−0.64,−0.69)
${Y_2}{\prime ^0}$= (0,0.02,−0.04,−0.13,−0.16),${X_2}^\prime $= (0,0.5,1,4,9)
${Y_3}^\prime$= (0,0.2,1,1.67,0.67),${X_3}^\prime$= (0,3,12,18,44)
③求$\left| {{{Y'}_{si}}} \right|$,$\left| {{{X'}_{sj}}} \right|$和$\left| {{{X'}_{sj}} - {{Y'}_{si}}} \right|$
④求灰色相对关联度
同理可以计算其余灰色相对关联度
γ11 = 0.527 7 γ12 = 0.531 5 γ13 = 0.569 4
γ21 = 0.661 0 γ22 = 0.523 3 γ23 = 0.504 5
γ31 = 0.545 9 γ32 = 0.676 2 γ33 = 0.533 3
得到相对关联矩阵
取θ = 0.5,则
从绝对关联矩阵A来看,A中的各行元素基本 满足εi3 > εi1 > εi2,i = 1,2,3; 故X3优于X1和X2,所 以X3为最优因素。εi1中两项大于εi2,一项小于εi2,但总的$\sum\nolimits_{i=1}^{3}{{{\varepsilon }_{i1}}}>\sum\nolimits_{i=1}^{3}{{{\varepsilon }_{i2}}}$,所以X1准优于X2。也就是 说,在药物与细胞吞噬研究中,药物分子的表面电荷是主要影响因素,药物形状的影响次之,药物尺寸影响相对较小。这些现象也与文献[3, 10, 11, 12]报道的结果相一致。
ε2j中有两项大于其他两行的数值,一项ε22较小,总的$\sum\nolimits_{j=1}^{3}{{{\varepsilon }_{2j}}}>\sum\nolimits_{j=1}^{3}{{{\varepsilon }_{1j}}}>\sum\nolimits_{j=1}^{3}{{{\varepsilon }_{3j}}}$,y2准优于y1、准优于y3,结果说明,在药物与细胞吞噬作用表达中内化百分率优于内化速率、优于内化指数。
在相对关联序列B中,各个行列相关指数比较接近,但存在$\sum\nolimits_{j=1}^{3}{{{\gamma }_{1j}}}$>$\sum\nolimits_{j=1}^{3}{{{\gamma }_{2j}}}$>$\sum\nolimits_{j=1}^{3}{{{\gamma }_{2j}}}$。所以,X1准优于X2、准优于X3,即因素颗粒形状影响较大,颗粒尺度影响次之,表面电荷影响较小。
在综合关联矩阵C中,各行各列规律不明显,但存在$\sum\nolimits_{j=1}^{3}{{{\rho }_{1j}}}$>$\sum\nolimits_{j=1}^{3}{{{\rho }_{3j}}}$>$\sum\nolimits_{j=1}^{3}{{{\rho }_{2j}}}$,所以X1准优于X3、准优于X2。这表明颗粒形状影响较大,表面电荷影响次之,颗粒尺度影响较小。
后两种分析结果和第1种结果有差异,这是因为绝对关联序列是从绝对量的关系上考虑,相对关联序列是考察各时刻观测数据相对于始点的变化速率,综合关联序列则是综合了绝对量的关系和变化速率的关系后考虑的。一般情况下根据需要选择1种灰色关联度即可。因为3组数据选自3个侧重面,所以以第1种绝对关联序列为准。
1.4 对相关实验现象的分析He等[12]研究结果表明,罗丹明B羧甲基壳聚糖接枝纳米颗粒 (RhB-CMCNP) 和罗丹明B标记壳 聚糖盐酸化物接枝纳米颗粒 (RhB-CHNP) 的表面电荷明显影响细胞的吞噬行为,细胞的吞噬百分数随着表面电荷的增加而增加 (包括正负电荷)。对比RhB- CMCNP (zeta电位值−25 mV,颗粒大小150 nm) 和RhB-CHNP (25 mV,150 nm); RhB-CMCNP (−25 mV,500 nm) 和RhB-CHNP (25 mV,300 nm),后者的吞噬百分数分别是前者的1.3和1.1倍,当zeta电位的绝对值相同时,正电荷比负电荷显示更高的吞噬百分率。药物尺寸也影响吞噬百分率,对比RhB-CMCNP (−25 mV,150 nm) 和RhB-CMCNP (−25 mV,500 nm); RhB-CHNP (25 mV,150 nm) 和RhB-CHNP (25 mV,300 nm),结果表明,后者的吞噬百分率分别是前者的1.2和1.1倍。
Xiao等[10]研究表明,在相似颗粒尺度 (17~27 nm) 下,PEG5000接枝8个胆酸的树枝状单分子在水中自组装成表面带电荷的纳米胶束PEG5000-CA8NPs,其表面电荷在巨噬细胞吞噬过程中起到非常重要的作用。正表面电荷显著地增加了PEG5000-CA8NPs细 胞摄取效率,在2 h孵化后,小鼠RAW 264.7巨噬细胞的摄入效率,带有不同电荷的zeta值18.5、29.5和37 mV分别为中性zeta值3.6 mV的1.9、3.5和5.9倍。相反,负表面电荷降低PEG5000-CA8NPs的摄取效率。在巨噬细胞的摄取中,调理素产生很大的影响,各种表面电荷的PEG5000-CA8NPs被预孵化,用新鲜小鼠血清调理作用后,巨噬细胞摄取负电荷离子的能力和没有调理的相比显著增加,但调理后摄取的正离子电荷降低。以上两例说明表面电荷对细胞和药物摄取产生很大影响。
细胞对药物的吞噬作用过程可分为3步,首先是药物被血液中的调理素,主要包括免疫球蛋白 (IgG、IgM) 和补体成分 (C1~C9) 等作用蛋白识别; 其次是吞噬性细胞对受调理素作用的药物吸附及吸收; 最后,药物与溶酶体发生融合并降解、释放其内部包载的药物。药物的表面电荷、形态和粒径均会影响细胞对其吞噬作用。
表面带有正或负电荷药物比中性药物更容易与巨噬细胞结合被吞噬,其原因是药物表面的负或正电荷可以与细胞发生相互 (静电) 吸引,或与特定受体发生相互吸引、静电吸引等使药物更易与细胞结合。
而药物和细胞结合也是一个运动过程,图 1中Ω≤45°的形状有利于药物运动,具有这类形状的药物颗粒于介质中运动时,在相同体积情况下其迎流面积 (指正对着流体面积) 相对较小。按照流体力学理论,它遇到的黏滞阻力就小,流体力学中用Stokes公式描述颗粒运动所受到阻力[24]:

其中,η、r和v分别表示介质的黏度、颗粒的迎流半径和运动速度。可见,颗粒的迎流半径较小时,运动时遇到的黏滞阻力就小,这与实验中观察到Ω较小的情形相对应。
按照静电学理论[25],纺锤状颗粒的两头也有利于表面电荷的聚集 (即静电学所谓的尖端效应),使其两头电荷密度增大,增加了与细胞之间的静电吸引力,有利于内化过程的进行。
纳米药物的形态、表面电荷和大小对药物在细胞内作用有很大的影响,不仅要从单个影响因素考虑,而且它和颗粒的整体性质以及所作用细胞的性质和体内环境等有关。
2 结论本文运用多因素灰色理论,综合分析了纳米药物的表面物理化学性质、形态和尺度大小的作用。分析表明,在药物和细胞作用过程中,表面zeta电位对药物的吸收过程起较大作用,其次是药物的形状和尺度。不同药物形状相比,仿锤球状药物越尖吸收越好。药物颗粒大小的影响也不容忽视,一般情况下颗粒越小吸收越好。
| [1] | Yoo JW, Doshi N, Mitragotri S. Adaptive micro and nanoparticles:temporal control over carrier properties to facilitate drug delivery[J]. Adv Drug Deliv Rev, 2011, 63:1247-1256. |
| [2] | Venkataraman S, Hedrick JL, Ong ZY, et al. The effects of polymeric nanostructure shape on drug delivery[J]. Adv Drug Deliv Rev, 2011, 63:1228-1246. |
| [3] | Yang YF, Xie XY, Yang Y, et al. A review on the influences of size and surface charge of liposome on its targeted drug delivery in vivo[J]. Acta Pharm Sin (药学学报), 2013, 48:1644-1650. |
| [4] | Champion JA, Mitragotri S. Role of target geometry in phagocytosis[J]. Proc Natl Acad Sci USA, 2006, 103:4930-4934. |
| [5] | Champion JA, Mitragotri S. Shape induced inhibition of phagocytosis of polymer particles[J]. Pharm Res, 2009, 26:244-249. |
| [6] | Gratton SEA, Ropp PA, Pohlhaus PD, et al. The effect of particle design on cellular internalization pathways[J]. Proc Natl Acad Sci USA, 2008, 105:11613-11618. |
| [7] | Geng Y, Dalhaimer P, Cai S, et al. Shape effects of filaments versus spherical particles in flow and drug delivery[J]. Nat Nanotechnol, 2007, 2:249-255. |
| [8] | Roser M, Fischer D, Kissel T. Surface-modified biodegradable albumin nano-and microspheres. II:effect of surface charges on in vitro phagocytosis and bio-distribution in rats[J]. Eur J Pharm Biopharm, 1998, 46:255-263. |
| [9] | Hirn S, Behnke MS, Schleh C, et al. Particle size-dependent and surface charge-dependent biodistribution of gold nanoparticles after intravenous administration[J]. Eur J Pharm Biopharm, 2011, 77:407-416. |
| [10] | Xiao K, Li YP, Luo JT, et al. The effect of surface charge on in vivo biodistribution of PEG-oligocholic acid based micellar nanoparticles[J]. Biomaterials, 2011, 32:3435- 3446. |
| [11] | Yu N, Li J, Hong D, et al. Cholesterol derivatives based charged liposomes for doxorubicin delivery:preparation, in vitro and in vivo characterization[J]. Theranostics, 2012, 2:1092-1103. |
| [12] | He CB, Hu YP, Yin LC, et al. Effects of particle size and surface charge on cellular uptake and biodistribution of polymeric nanoparticles[J]. Biomaterials, 2010, 31:3657- 3666. |
| [13] | Deng JL. Grey Control System (灰色控制系统)[M]. Wuhan:Huazhong Univ Sci Press, 1988. |
| [14] | Yang YC. Effect of shipping aid policies on the competitive advantage of national flagged fleets:comparison of Taiwan, Korea and Japan[J]. Trans Policy, 2014, 35:1-9. |
| [15] | Yan JH, Li L. Multi-objective optimization of milling parameters-the trade-offs between energy, production rate and cutting quality[J]. J Clean Prod, 2013, 52:462-471. |
| [16] | Senthilkumar N, Tamizharasan T, Anandakrishnan V. Experimental investigation and performance analysis of cemented carbide inserts of different geometries using Taguchi based grey relational analysis[J]. Measurement, 2014, 58:520-536. |
| [17] | Xi YJ, Wu XM, Zheng XR, et al. Grey analysis of relationships between abundance of Gymnodinium spp. and seawater physicochemical factors[J]. Fish Sci (水产科学), 2014, 33:410- 416. |
| [18] | Qu YH, Zhang XL, Duan JL. Spatial variation of land use diversity patterns and its correlation analysis for the case areas in the central Henan province[J]. J Anhui Agri Univ (安徽农业科学), 2014, 41:253-259. |
| [19] | Hou XJ, Jiang B. Gray correlation analysis between the lycopene and the quality character of processing tomato[J]. Agri Mech Res (农机化研究), 2014, 3:54-57. |
| [20] | Wang XF, Zou N, Zhou YH, et al. Effectiveness analysis of grey correlation theory in motor broken bars fault identification[J]. Mine Electromech (煤矿机电), 2014, 5:96-99. |
| [21] | Hu W. The preparation method of polycarboxylate superplasticizer based on the gray relativity theory[J]. Eng Mater Equip Mun Tech (市政技术), 2015, 33:171-173. |
| [22] | Liu SF, Xie NM, et al. Gray System Theory and Applications (灰色系统理论及其应用)[M]. 4th ed. Beijing:China Science Press, 2008. |
| [23] | Zhou XW. The Study on the Grey Relational Degree and Its Application (灰色关联度的研究与应用)[D]. Jilin:Jilin University, 2007. |
| [24] | Hiemenz PC, Rajagopalan R. Principles of Colloid and Surface Chemistry[M]. New York:Marcel Dekker Inc, 1977:101-106. |
| [25] | Zhao KH, Chen XM. Electromagnetics (电磁学)[M]. Beijing:People Education Press, 1979:100-104. |
 2015, Vol. 50
2015, Vol. 50