| GA-BP神经网络模型在稀土矿边坡位移监测中的应用 |
b. 江西理工大学土木与测绘工程学院,江西 赣州 341000
b. School of Civil and Surveying & Mapping Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, Jiangxi, China
离子型稀土矿原地浸矿是注入溶浸液将吸附态矿物离子交换浸出的采矿方法,具有不破坏地表植被、无尾矿库、资源回收利用率高等优点,是国家大力推广的离子型稀土矿开采方法[1-3]。长期大量注入浸矿液,使矿土强度减弱、孔隙增大,矿体抗剪强度降低,极易发生稀土矿边坡滑塌[4-6]。滑坡会危及矿山和周围群众的安全,因此必须加强对原地浸矿的稀土边坡稳定性监测及灾害预警,为指导稀土矿山安全生产、保障群众的生命财产安全提供保障。
目前边坡变形[7]预测的常用方法有:灰色模型[8]、神经网络[9]、向量机序列[10]等方法。蒋刚等利用灰色系统建立了单一测点的GM(1,1)边坡变形预测模型,该模型是一种单变量灰色预测模型,只是对监测对象的局部变形研究,存在模型精确度不高等缺点[11];范新宇等利用BP神经网络模型预测库区高边坡变形,但BP神经网络算法收敛速度慢,在较大的搜索空间网络易陷入局部极限值[12]。潘平通过小波神经网络理论预测边坡位移,研究表明该预测方法效率较高,收敛速度快,但模型精确度不佳[13]。
针对以上不足,本文利用强大的全局寻优能力以及较快的收敛速度的遗传算法对BP神经网络初始权值和阈值进行优化,再利用BP-ANN算法搜索最优解,从而得到改进后的BP神经网络算法,即GA-BP神经网络算法。将此算法应用于稀土矿边坡位移监测分析工作,验证该方法在边坡变形监测中的适用性。
1 稀土矿边坡工程监测背景 1.1 工程概况龙南某稀土矿区位于江西省龙南市东南10 km,面积为23.306 km2,区内地貌为风化低山丘陵地貌,山顶浑圆,地形从东到西走向,沟谷纵横起伏。矿区气候属亚热带季风型,矿区年最高气温为39.3 ℃,最低气温-7.9 ℃。矿区内花岗岩全风化层的全部或部分是矿体,矿体的分布与花岗岩全风化层的分布情况基本一致,呈似层状沿花岗岩全风化层分布,且大体连续成片,具有面型风化壳特征,沿地形变化呈波状起伏展布。
矿体总体形态简单,但矿体单体而言,其平面形态略为复杂,多呈阔叶状。矿体剖面形态简单,总体呈似层状波浪起伏。各矿体单体剖面上呈盖形,矿体由中部向四周倾斜,沿山脊矿体倾斜较缓,一般约为5°~10°;沿山坡矿体倾斜较陡,多为20°~30°,山坡局部坡度可达40°。矿区矿体垂向上厚度多为6~10 m,最小厚度为4.7 m,最大厚度达13.0 m。据勘探浅井工程统计,矿体平均厚度为8.1 m,其中山顶矿体最厚,一般为9~13 m;山脊矿体厚度次之,一般为6~9 m;山坡两翼及坡脚矿体厚度较薄,一般为4~6 m。矿体产状较为平缓,平均厚度中等,为似层状面型表露矿体,形态较为简单,受地貌形态的制约,其产状和厚度变化明显。
因矿体赋存在白云母、黑云母花岗岩风化壳中,风化壳厚且松散,矿体覆盖层较小,强风化带裂隙十分发育,岩体破碎,岩矿均属不坚固岩组。受地形地貌及风化程度差异的影响,导致了风化壳在垂直剖面上的地层差异,自上而下可划分为:表土层、全风化层、半风化层、基岩层,具体位置关系如图 1所示。
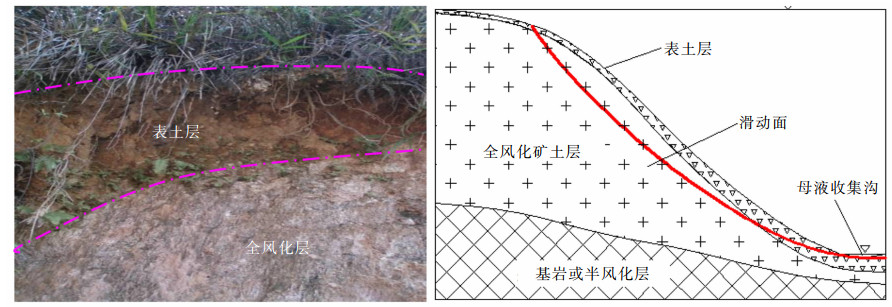 |
| 图 1 龙南某稀土矿赋存位置剖面示意 Fig. 1 Profile of occurrence location of a rare earth mine in Longnan |
1.2 边坡在线监测方案
龙南某稀土矿采用原地浸矿工艺,溶浸液、雨水是诱发滑坡的最主要因素。当潜滑体土壤的含水率增大并趋向饱和时,土壤的内聚力(c)减小,从而降低了土体的抗剪强度,导致滑坡发生[14]。因山体内部溶浸液对电子元件有侵蚀作用,故渗压监测选择光纤光栅微型渗压计,坡体水饱和度监测选择数字式土壤水分计。同时考虑到降雨对矿区地质灾害的诱发作用,需要布置一个雨量监测点,考虑到本矿山采用原地浸矿回收母液的开采方式,在矿体或处于高地下水区域的边坡或滑坡体需要增设一个地下水位观测点。具体传感器布置如图 2所示。
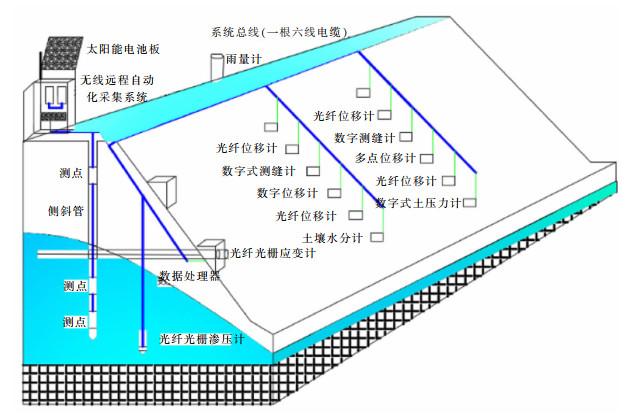 |
| 图 2 山体剖面传感器布网与埋设示意 Fig. 2 Mountain profile sensor network and embedding map |
对于本矿山潜在的地质灾害点(例如可能的滑坡体和饱水边坡),以其变形监测为重点,即对监测对象在表面布设若干表面位移测点,同时在两个不同高程各布设一套内部变形仪器,共同监测潜在滑坡体的位移变形,实时监测其稳定状况。表面位移监测传感器选用数字式测缝计和新型光纤光栅位移计,位移监控使用数字式测缝计,由光纤光栅组成的传感器则可实现回收再利用,内部变形传感器选用多点位移计或数字式测斜仪。重点研究位移监测在稀土矿边坡稳定性方面的应用。
2 算法模型基本原理 2.1 BP神经网络人工神经网络(Artificial Neural Network,ANN),是1980年后兴起的热点算法模型,主要通过模仿大脑神经元结构和其反射过程建立数据处理模型[15-17]。BP神经网络属于人工神经网络的一种,BP神经网络是一种多层前馈神经网络,由输入层、隐含层、输出层、输入向量、隐权值、阈值、隐含层的激励函数、输出层激励函数和输出函数组成[18-20]。
2.2 遗传算法BP优化神经网络机理虽然BP神经网络具有容错能力、自适应能力强大等优点,但BP神经网络算法收敛速度慢,在较大的搜索空间网络易陷入局部极限值[21-22]。为了改进BP神经网络,本文结合GA(遗传算法)的全局搜索能力,采用GA算法对ANN的初始权值和阈值进行优化,再利用BP-ANN算法搜索最优解,从而得到改进后的BP神经网络算法,即GA-BP神经网络算法,优化后算法流程图如图 3所示。
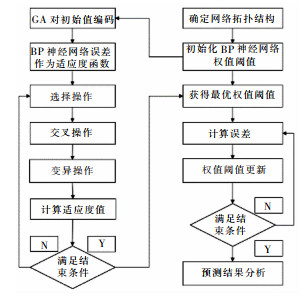 |
| 图 3 GA-BP算法流程 Fig. 3 GA-BP algorithm flow chart |
3 GA-BP神经网络模型的构建 3.1 模型与数据介绍
采用MatlabR2018a对监测数据进行算法预测,为了改进BP-ANN,结合GA的全局搜索能力,采用GA算法对ANN的初始权值和阈值进行优化,再利用BP-ANN算法搜索最优解。GA-BP算法大体包括以下步骤:BP-ANN的建立、GA对神经网络的权值和阈值的优化、网络学习、程序测试与仿真。
以龙南某稀土矿监测点5的130组边坡数据作为研究对象,前125组作为预测模型的训练样本,剩下5组作为模型的测试样本,通过BP神经网络模型、GA-BP神经网络模型来分析监测点监测数据的4种误差,监测点5号、6号的位移累加值如图 4所示。
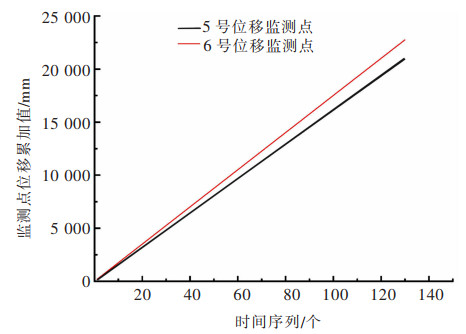 |
| 图 4 5号、6号监测点位移数据 Fig. 4 Displacement data of No.5 and No.6 monitoring points |
3.2 GA与BP相关参数设置 3.2.1 BP参数设置
1)输入层和输出层使用zeros函数获取。调用zeros函数生成全零矩阵,调用格式如下:A=zeros(m, n),本程序输入变量需生成130行5列的全零矩阵,输出变量需生成125行1列的零矩阵,调用输入函数“input”,调用输出函数“output”,以125组数据作为训练数据,5组数据作为测试数据。即输入层节点数为5,输出层节点数为1。
2)隐含层节点的确定过程。本模型采用3层BP神经网络(ANN)模型,隐含层节点数量不同,均方误差也不相同。为了得到较优隐含层节点个数,使模型均方误差最小,采用数量经验公式(1)确定隐含层节点个数。
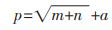
|
(1) |
式(1)中:p表示隐含层节点个数;n为输入层节点个数;m为输出层节点个数;a表示0~10范围内的常数。
3)其他BP参数,如学习速率、训练次数、训练目标误差等。为了提高网络的拟合精度和泛化能力,通过反复比较确定网络参数,训练次数为1 000次,最小误差为0.000 1,显示频率为0.01,动量因子为0.01,最小性能梯度为1×10-6,网络学习速率为0.01。
3.2.2 GA参数设置选用遗传算法对BP神经网络的权值和阈值进行优化,在遗传算法中采用两点交叉法交换染色体,采用高斯变异法对染色体进行变异,遗传算法参数选取如下:选取种群规模为60,种群进化代数为80,交叉概率取0.8,变异概率取0.008。
3.3 遗传算法优化BP神经网络 3.3.1 优化变量使用遗传算法求解优化问题时,对于优化变量有3种编码方式:向量形式编码、二进制编码、矩阵形式编码。由于阈值和权值选用的是矩阵函数,为方便对每个元素都进行优化,先将元素分别取出,然后按取的顺序放入向量(染色体)中完成编码。权重和阈值的经验范围为[-1, 1]。
3.3.2 适应度函数的计算适应度函数的优劣直接影响到GA(Genetic Algorithm)的性能,设置适应度函数要根据实际问题要求而设计,所以适应度公式选择为求解最小的均方误差。在使用遗传算法优化后,适应度函数值越小,表明训练越准确,预测精度更好。适应度函数的计算公式为:
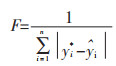
|
(2) |
由于确定了优化变量和适应度函数,所以只需要将遗传算法视为“黑箱”优化器,即可以输出最小误差和最优解变量,再将变量赋给BP神经网络的阈值和权值相应位置,然后进行优化后的BP训练与测试。具体步骤和流程见图 3。
4 预测结果分析 4.1 BP神经网络的最佳隐含层和最小均方误差本模型采用3层BP神经网络(ANN)模型,输入层节点个数为5,输出层节点个数为1,不同隐含层均方误差如图 5所示,在隐含层节点数范围内,随隐含层节点数从小到大的变化过程中,整个神经网络预测结果的准确率也随之发生变化:BP-ANN程序运算得出监测点5和监测点6的最佳隐含层节点数分别为14和7,均方误差均取得最小值,分别为0.059 55和0.016 93。
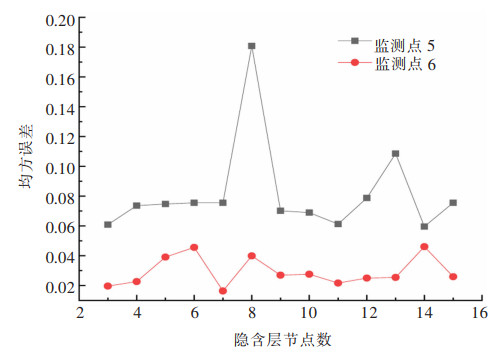 |
| 图 5 不同隐含层均方误差 Fig. 5 Mean square error of different hidden layers |
同时发现随着隐含层节点数增加,监测点5均方误差波动较大,在隐含层节点数为8时达到最大,而且均方误差值远超于其他节点,可能是因为遗传算法优化的BP神经网络是为了能够有更大的可能性获得全局最优解,本质上仍是概率问题,所以可能存在某个个体不符合整体趋势,在概率上未能得到最优解,从而出现较大的误差。随着隐含层节点数增加,监测点6均方误差变化不大,隐含层中第8节点至第13节点均方误差的逐渐减小,由于随着隐含层神经元数量的增加,一方面训练时间随之加长,另一方面可能造成模型泛化能力下降。
4.2 遗传算法进化曲线在使用遗传算法优化后,适应度函数值越小,表明训练越准确,预测精度更好。由图 6可知遗传算法最佳适应度值为4.152 76×10-5,平均适应度值为2.904 24×10-4,说明了GA-BP算法适应度函数选取恰当。
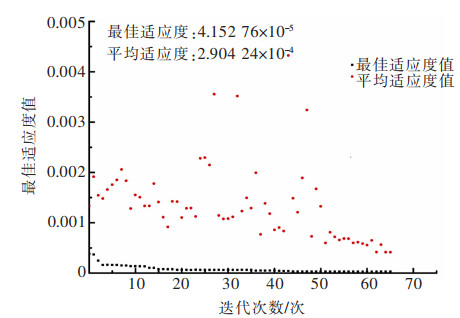 |
| 图 6 最佳适应度图 Fig. 6 Optimal fitness figure |
4.3 基于GA-BP的边坡位移预测结果对比分析
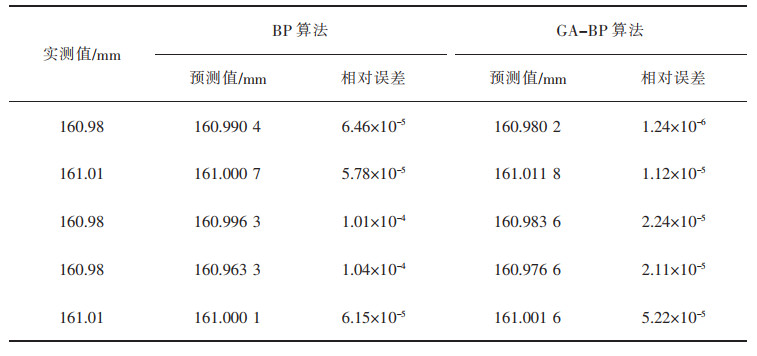
针对龙南某稀土矿的剩余5组测试样本分别采用BP神经网络模型、GA-BP神经网络模型进行分析,分析对比BP神经网络、GA-BP神经网络这2种模型的相对误差、平均绝对误差、均方误差、均方误差根、平均绝对百分比误差,具体数值见表 1。以此来衡量GA-BP神经网络模型预测稀土矿边坡的位移监测的性能。
| 表 1 真实值和预测值对比 Table 1 Comparison of real and predicted values |
 |
| 点击放大 |
BP神经网络算法和GA-BP神经网络算法真实值与预测值的相对误差(扩大1 000倍)见图 7,BP神经网络算法相对误差先略微减小然后增大最后又减小,而GA-BP神经网络算法的相对误差则呈现一直增大的趋势,近似线性变化,但其相对误差的最大值仍小于BP神经网络算法相对误差的最小值。BP神经网络算法平均相对误差7.78%,GA-BP神经网络算法的平均相对误差2.16%,在相对误差方面,GA-BP神经网络算法优化到传统的BP神经网络算法误差的1/3以下。
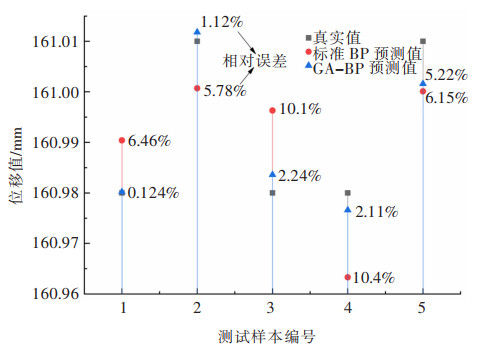 |
| 图 7 真实值与预测值对比 Fig. 7 Comparison between real and predicted values |
GA-BP神经网络算法得到的预测值基本与真实值相吻合,BP神经网络算法得到的预测值相对于GA-BP神经网络算法得到的预测值与真实值相差较大,GA-BP神经网络算法相对误差较BP神经网络算法波动性较小、算法精度较高,用遗传算法(GA)优化后的BP-ANN算法模型对稀土矿边坡的位移监测效果更好。
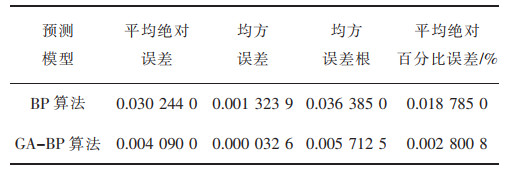
对比表 2前后预测模型误差可知,BP神经网络算法误差的变化规律高低起伏,在[0.001,0.04]之间波动,波动的范围较GA-BP神经网络大,而GA-BP神经网络算法4种误差在[0.000 03,0.005]之间波动,波动范围较小,且呈规律性变化,都在0.003 5左右波动,有向0.003 5收敛的趋势。GA-BP神经网络算法在平均绝对误差、均方误差、均方误差根、平均绝对百分比误差分别比BP神经网络算法降低86.5%、97.5%、84.5%、85.1%,GA-BP神经网络算法误差优化到传统的BP神经网络算法的1/3以下。GA-BP神经网络算法在4种误差方面要优于BP神经网络算法,更具有优越性,在4种误差方面用遗传算法(GA)优化后的BP-ANN算法模型对稀土矿边坡的位移监测效果更好,见图 8。
| 表 2 预测模型误差 Table 2 Prediction model error |
 |
| 点击放大 |
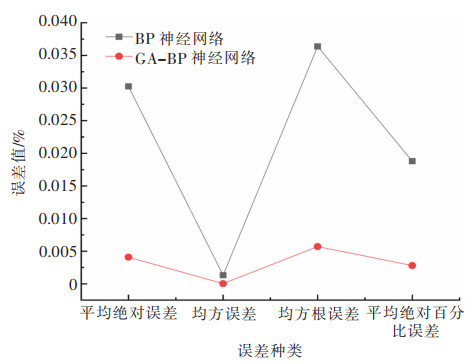 |
| 图 8 模型误差对比 Fig. 8 Model error comparison |
5 结论
引入了BP神经网络和遗传算法,利用遗传算法对BP神经网络模型初始权值和阈值进行改进优化,将其应用于稀土边坡位移预测分析,主要得出以下结论:
1)使用遗传算法对BP神经网络算法模型的权值和阈值进行优化,监测点平均相对误差7.78%减小到优化后的2.16%,模型精度有明显提升。
2)GA-BP神经网络算法模型运用于稀土矿边坡位移预测分析,监测点的平均绝对误差、均方误差、均方误差根、平均绝对百分比误差分别比BP神经网络模型降低了86.5%、97.5%、84.5%、85.1%。GA-BP神经网络算法模型在这4种误差方面均优于BP神经网络算法模型,表明该模型在稀土矿边坡位移监测中具有较高的适用性。
3)在排除外界干扰的情况下,GA-BP神经网络预测值与实测值基本吻合。GA-BP神经网络算法模型能有效地预测了稀土矿边坡的位移变化趋势,可作为稀土矿边坡位移监测预警分析的一种辅助手段。
| [1] |
饶运章, 张永胜, 饶睿, 等. 离子型稀土原地浸矿边坡稳定影响因素敏感性分析[J].
矿业研究与开发, 2015, 35(9): 60–63.
|
| [2] |
ZHANG, ZHENGYAN HE, JUNXIA YU, et al. Novel solution injection technology for in-situ leaching of weathered crust elution-deposited rare earth ores[J].
Hydrometallurgy, 2016, 164: 248–256. DOI: 10.1016/j.hydromet.2016.06.015. |
| [3] |
代晶晶, 王瑞江, 王登红, 等. 基于IKONOS数据的赣南离子吸附型稀土矿非法开采监测研究[J].
地球学报, 2014(4): 503–509.
|
| [4] |
饶睿, 李明才, 张树标, 等. 离子型稀土原地浸矿采场滑坡特征及防控试验研究[J].
稀土, 2016, 37(6): 26–31.
|
| [5] |
胡世丽, 洪本根, 罗嗣海, 等. 裸脚式稀土矿山原地浸矿的边坡稳定性分析[J].
工程地质学报, 2017, 25(1): 110–116.
|
| [6] |
陈荣军, 廖伟成, 张耀平, 等. 某离子型稀土矿边坡稳定性分析[J].
有色金属科学与工程, 2015, 6(4): 111–115.
|
| [7] |
江胜华, 宋韫皓, 孙伟贺, 等. 基于粘贴式智能石块的边坡大变形监测方法[J].
重庆大学学报, 2020, 43(5): 76–83.
|
| [8] |
HU Z N, GAO C, SU Q H. A novel evolutionary algorithm based on even difference grey model[J].
Expert Systems With Applications, 2021, 176: 114898. DOI: 10.1016/j.eswa.2021.114898. |
| [9] |
李克钢, 张重庆. 基于时间序列的神经网络建模及边坡位移预测[J].
地下空间与工程学报, 2009, 5(增刊1): 1418–1421.
|
| [10] |
马文涛. 基于灰色最小二乘支持向量机的边坡位移预测[J].
岩土力学, 2010, 31(5): 1670–1674.
DOI: 10.3969/j.issn.1000-7598.2010.05.055.
|
| [11] |
蒋刚, 林鲁生, 刘祖德, 等. 边坡变形的灰色预测模型[J].
岩土力学, 2000(3): 244–246.
DOI: 10.3969/j.issn.1000-7598.2000.03.013.
|
| [12] |
范新宇, 杨天俊, 高凯, 等. BP神经网络模型在库区高边坡变形预测中的应用[J].
西北水电, 2017(1): 72–74.
DOI: 10.3969/j.issn.1006-2610.2017.01.019.
|
| [13] |
潘平. 基于小波神经网络理论的边坡位移预测[J].
成都理工大学学报(自然科学版), 2006(2): 176–180.
DOI: 10.3969/j.issn.1671-9727.2006.02.010.
|
| [14] |
罗嗣海, 袁磊, 王观石, 等. 浸矿对离子型稀土矿强度影响的试验研究[J].
有色金属科学与工程, 2013, 4(3): 58–61.
|
| [15] |
谢晨月, 袁泽龙, 王建春, 等. 基于人工神经网络的湍流大涡模拟方法[J].
力学学报, 2021, 53(1): 1–16.
|
| [16] |
张驰, 郭媛, 黎明. 人工神经网络模型发展及应用综述[J].
计算机工程与应用, 2021, 57(11): 57–69.
DOI: 10.3778/j.issn.1002-8331.2102-0256.
|
| [17] |
HUSSINA S, KHAN H, GUL S, et al. Modeling of photolytic degradation of sulfamethoxazole using boosted regression tree (BRT), artificial neural network (ANN) and response surface methodology (RSM); energy consumption and intermediates study[J].
Chemosphere, 2021, 276: 130151. DOI: 10.1016/j.chemosphere.2021.130151. |
| [18] |
田乃满, 兰恒星, 伍宇明, 等. 人工神经网络和决策树模型在滑坡易发性分析中的性能对比[J].
地球信息科学学报, 2020, 22(12): 2304–2316.
DOI: 10.12082/dqxxkx.2020.190766.
|
| [19] |
文必洋, 汤文成, 田应伟. 基于BP神经网络的高频雷达有效浪高场反演[J].
华中科技大学学报(自然科学版), 2021, 49(4): 114–119.
|
| [20] |
LI Y, HUIHUI G, JIA X W. An automatic crisis information recognition model based on BP neural networks[J].
Journal of Ambient Intelligence and Humanized Computing, 2021: 1–12. |
| [21] |
何丹, 林来鹏, 李小勇, 等. 基于改进粒子群算法优化BP神经网络的废水处理软测量模型[J].
华南师范大学学报(自然科学版), 2021, 53(2): 114–120.
|
| [22] |
LIU H J, LIU J H, WANG Y S, et al. Identification of grouting compactness in bridge bellows based on the BP neural network[J].
Structures, 2021, 32: 817–826. DOI: 10.1016/j.istruc.2021.02.069. |
 2022, Vol. 13
2022, Vol. 13


