| 基于变权物元可拓模型的非煤矿山安全标准化等级评价 |
随着我国矿山行业的进一步发展,矿山安全生产形势也在逐渐好转,而由国家所推行的金属非金属矿山安全标准化在其中发挥着重要作用[1-2]。目前,我国大多数非煤矿山企业已经基本完成了矿山安全标准化体系的创建,对其安全标准化体系进行考核与评估,能有助于企业完善和改进自身安全标准化体系[3-4],加强企业在安全生产中的规范性,同时促进整个矿山行业的安全标准化进程[5-7]。因此,准确完成对非煤矿山安全标准化的评价工作是矿山安全生产建设中必不可少的一环。
近年来,许多学者运用不同方法对企业安全标准化评价进行了研究,主要有模糊综合评价法[8]、层次分析法[9]、未确知测度理论[10]、Fisher判别法[11]等。虽然这些方法都取得了较好的成果,但由于非煤矿山安全标准化评价受诸多具有模糊性和可变性等特点的因素所控制,且因素之间往往会相互影响,从而增大了评价过程的复杂性和不确定性,使得上述研究方法都具有一定的局限性。针对非煤矿山安全标准化评价中的这些问题,物元可拓理论能够为其提供合理可行的解决途径。
物元可拓理论是一种能够有效解决评价对象不相容和不确定性问题的研究方法[12-13],被广泛应用于各类工程领域的综合评价问题中[14-16]。其总体思路是通过建立多指标物元评判模型,将所有评价指标转化为定量指标,再以定量数值来确定最终结果[17-18]。传统物元可拓模型通常是运用常权或简单的关联度函数来确定权重,再采取最大隶属度准则来进行等级评定[19]。然而通过常权法来确定指标权重会使得权重受主观因素影响较大且无法体现评价对象在评价体系中的主动参与;最大隶属度准则也有着在某些情况下无法反映评价对象自身界限的模糊性和易丢失评价信息的缺陷[20]。为弥补这些不足和缺陷,本文将变权理论[21-22]与物元可拓理论相结合,在传统的物元可拓模型的基础上进行改进。首先,由变权理论来确定指标权重;其次,运用贴近度来代替最大隶属度准则确定评价等级;最后,引入敏感性分析来确定评价敏感性指标。由此可构建变权物元可拓模型,并基于该模型对非煤矿山安全标准化体系进行评价,从而获得准确可靠的评价结果。
1 建立变权物元可拓模型 1.1 确定评价指标体系设需要评价的非煤矿山安全标准化体系有m个,安全标准化评价指标X有n个,第i(i=1,2,…,m)个待评价的非煤矿山在第j(j=1,2,…,n)个评价指标下的量值为uij,则待评价系统可用n维物元R=(M,X,U)来表示:
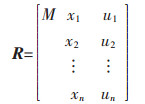
|
(1) |
式(1)中:M为待评的安全标准化体系;xj为安全标准化评价的第j个指标;uj为第j个指标的量值。
1.2 确定经典域、节域、待评物元1)确定经典域P。根据安全标准化评价相关分级标准,假定非煤矿山安全标准化等级可分为s级,则经典域P=(Pk,X, Uk),可表示为:
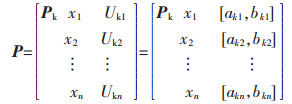
|
(2) |
式(2)中:Pk为非煤矿山安全标准化分级中的第k(k=1,2,…,s)等级;Ukj=[akj,bkj]为第k个等级中第j个指标的量值域,akj和bkj分别为该量值域的下限值和上限值。
2)确定节域Q。根据各项待评指标在全体评价等级中所对应的取值范围,由取值范围内的最小值和最大值即可得到节域Q=(Qc,X,Uc),可表示为:
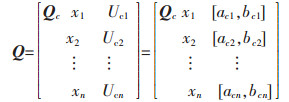
|
(3) |
式(3)中:Qc为安全标准化评价等级的全体;Ucj=[acj,bcj]为第j项指标在全体评价等级中的值域,acj和bcj分别为值域内的最小值和最大值。
3)确定待评物元Ri。根据待评矿山安全标准化体系的实际情况和既定的评分标准对各项评价指标进行打分,由此可得待评物元Ri=(Mi,X,Ui),可表示为:
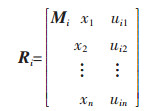
|
(4) |
式(4)中:Mi为第i个待评非煤矿山的安全标准化。
1.3 评价指标归一化处理因不同安全标准化评价指标的量纲可能存在差别,无法进行直接比较,为了便于分析,则需对每项指标进行归一化处理。归一化处理公式为:
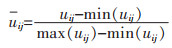
|
(5) |
式(5)中:uij=为归一化处理后的第i个非煤矿山中第j个安全标准化评价指标的量值;min(uij)和max(uij)分别为第j个指标的最小评分值和最大评分值。
1.4 变权理论确定指标权重各评价指标的权重值对最终评价结果的确定起着决定性作用,但在采用常权法来确定权重时,往往会因为评价过程中所存在的主观因素使得评价结果产生偏差。而采用变权理论确定评价指标权重能够有效地减小主观因素对评价结果的影响并体现待评物元在评价体系中的主动参与性。因此本文采用熵权法来确定评价指标的常权权重,并运用变权理论来对常权权重进行修正,从而确定变权权重,以使评价指标的权重能更好的体现各指标对待评物元所起的作用。
根据因素空间理论对变权理论的研究[23],可确定待评物元各项指标的变权权重ωij(X)的计算方法,设待评物元Ri的因素常权向量Wi=ωij,状态变权向量Si(X)=sij(X),则变权向量Wi(X)=ωij(X)可由常权向量和状态变权向量的Hadamard乘积表示,即:
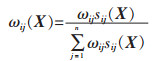
|
(6) |
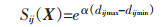
|
(7) |
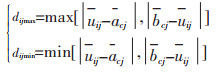
|
(8) |
其中:ωij为第j个指标的常权权重;acj和bcj分别为指标归一化后节域的下限值和上限值;α为变权因子,其数值大小表示对指标均衡性的要求,当α>0时,对指标的均衡性要求不高,当α<0时,对指标的具有一定的均衡性要求,当α=0时为常权模型。
1.5 贴近度计算运用最大隶属度准则进行等级评判时,存在着在一些情况下容易损失信息而造成评判结果低效或无效的缺陷。根据贴近度代替最大隶属度准则的研究[24],可知非对称贴近度能有效避开该缺陷,并确定待评物元Ri关于安全标准化评价等级k的非对称贴近度Nk(Ri)为:
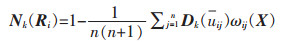
|
(9) |
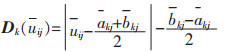
|
(10) |
式(10)中:Dk(uij)为指标归一化后的待评物元与经典域的距离;akj和bkj分别为指标归一化后经典域的下限值和上限值。
1.6 确定评价等级待评物元Ri的安全标准化等级k0可用下式来判断:
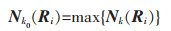
|
(11) |
利用式(5)将Ri关于各评价等级的贴进度进行归一化处理后得到Nk(Ri),则有
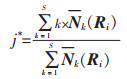
|
(12) |
式(12)中:j*为待评物元Ri的等级变量特征值,表示待评物元Ri偏向相邻等级的程度。
2 实例应用为验证变权物元可拓模型在非煤矿山安全标准化评价中的可行性和适用性,以江西某非煤矿山作为实例样本来进行分析。
2.1 安全标准化运行评价指标体系对非煤矿山安全标准化评价有影响的因素间往往具有一定的相互关系和相似性,为避免指标过多从而增大安全标准化评价的复杂性,或指标过少从而造成评价结果存在较大的偏差,本依据《金属非金属矿山安全标准化规范导则》[25]和安全标准化评价指标体系的相关研究[6, 10],结合矿山实际情况,从安全监管、安全保障、安全生产、安全绩效4个方面确定16个因素作为评价指标,构建安全标准化评价指标体系。其中,安全监管包含3个指标,安全保障包含8个指标,安全生产包含3个指标,安全绩效包含2个指标,具体如表 1所列。
| 表 1 安全标准化评价指标体系 Table 1 Evaluation index system of safety standardization |
 |
| 点击放大 |
在所构建的安全标准化评价体系的基础上,依据常用分级标准和矿山实际情况,将矿山安全标准化分为4个等级,分别为Ⅰ级(好)、Ⅱ级(较好)、Ⅲ级(一般)、Ⅳ级(不合格)。
根据上述安全标准化评价指标体系和分级标准,成立一个由10位专家组成的评审小组,每位专家通过自身专业知识和经验对待评矿山的各项评价指标进行评分,分值为0~10分。
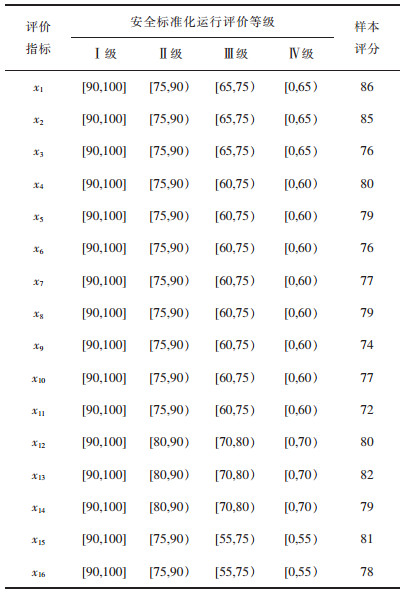
由于《金属非金属露天矿山安全生产标准化评分办法》只以总分来确定标准化等级,缺少各项指标的分级标准;而在相关文献中也仅是以相同的分级标准来规定每项指标的等级临界值,忽视了不同指标对评价结果影响程度的差异性。因此,本文在上述评分办法的基础上,结合矿山实际情况以及评审小组给出的建议,确定各评价指标的安全标准化分级标准。所得出的评价指标安全标准化等级分级标准和样本数值如表 2所列。
| 表 2 安全标准化评价指标分级标准及样本数值 Table 2 Classification standards and sample values of safety standardization evaluation indexes |
 |
| 点击放大 |
2.2 评价指标归一化
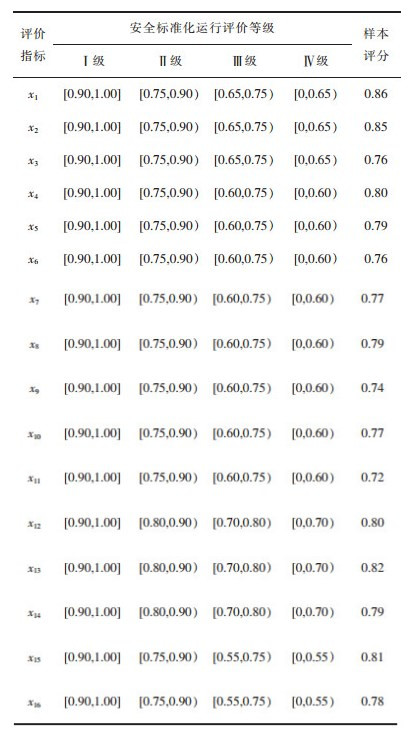
根据式(5)对表 2中的数据进行归一化处理,结果如表 3所列。
| 表 3 安全标准化评价指标归一化后分级标准及样本数值 Table 3 Classification standards and sample values of safety standardization indexes after normalization |
 |
| 点击放大 |
2.3 经典域、节域及待评物元
根据式(2)~式(4),并结合表 3即可确定归一化后的经典域P、节域Q及待评物元R1。

|

|
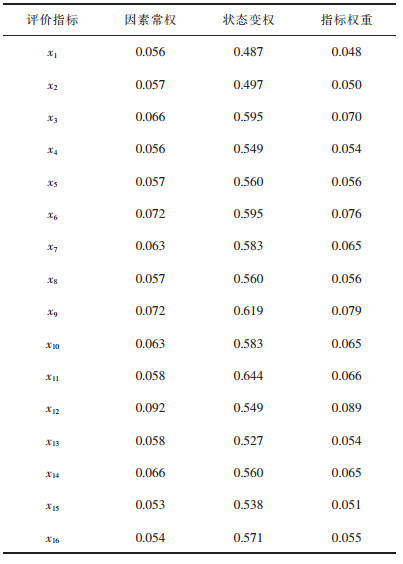
参照文献[14]中熵权法的计算过程来确定待评矿山各评价指标的常权权重ω1j;为确保各评价指标具有一定的均衡性,本文取变权因子α=-1,由此可根据式(6)~式(8)确定待评矿山各评价指标的状态变权s1j(X)及变权权重ω1j(X),结果如表 4所列。
| 表 4 安全标准化评价指标的权重 Table 4 Weights of evaluation indexes for safety standardization |
 |
| 点击放大 |
2.5 确定样本贴近度
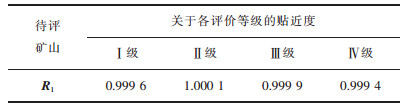
根据式(9)~式(10),可得出待评矿山R1关于各评价等级的贴近度,结果如表 5所列。
| 表 5 贴近度计算结果 Table 5 Results of calculating closeness degree |
 |
| 点击放大 |
2.6 矿山安全标准化评价结果
根据式(11)并结合表 5中,可确定实例矿山的安全标准化等级;再由式(12)计算得出矿山的等级变量特征值j*=2.255<2.5;由此可综合判定该矿山的安全标准化等级为Ⅱ级,且偏向于Ⅰ级的程度较大,表明该矿山的安全标准化运行状况较好。基于变权物元可拓模型所确定的评价等级与模糊综合评价法[8]的评判结果一致,表明该模型的评判结果是合理可靠的。
2.7 敏感性分析为进一步了解各项安全标准化评价指标对结果的影响,并从中找出对安全标准化评价结果有重要影响的敏感性指标,需对权重和等级变量特征值随着指标实测值的变化而改变的情况进行分析,从而确定所建模型对各指标值变化的敏感性。为保证分析结果的合理可靠,将各指标的敏感性程度进行量化处理,本文采用标准差来对其进行衡量。
当实例矿山的各项评价指标评分值分别以±10%、±20%、±30%、±40%、±50%的趋势变化时,指标权重和等级变量特征值j*的变化情况分别如图 1和图 2所示,并通过计算得出各指标的权重标准差和等级变量特征值标准差,结果如表 6所列。
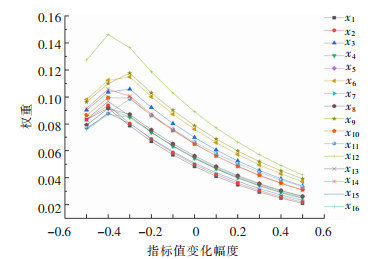 |
| 图 1 权重随指标值变化情况 Fig. 1 Variation of weights with index values |
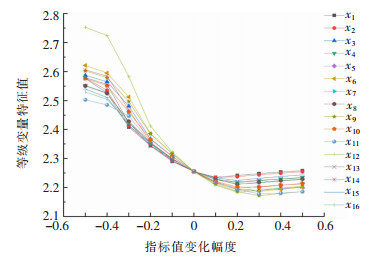 |
| 图 2 等级变量特征值随指标值变化情况 Fig. 2 Variation of eigenvalues with index values |
| 表 6 权重和等级变量特征值的变化幅度标准差 Table 6 Standard deviation of changes in weights and eigenvalues of rank variables |
 |
| 点击放大 |
由图 1可知,各项评价指标的权重整体上随着其评分值的增大而减小、减小而增大,但是当评分值减小到一定程度时,权重反而会随着评分值的减小而减小,同时各项指标达到极大值点时的变化幅度也有所不同。其中指标x6、x9、x12的权重变化趋势最为明显,指标x6和x9的权重在-30%点达到极大值,指标x12则在-40%点达到极大值。通过上述分析可确定,各评价指标的权重会随着指标评分值的变化而变化,且不同指标的权重变化规律存在一定的差异,这体现了评价指标在评价过程中的主动参与。
由图 2可知,随着指标值的增大,等级变量特征值j*的变化幅度较小,处于2.2~2.3的范围之间,这说明指标值的增大并不会改变矿山的安全标准化评价等级及其偏向Ⅰ级安全标准化的程度;而随着指标值的减小,j*逐渐变大,当指标值变化幅度达到-40%时,j*已经大于2.5,说明此时安全标准化评价等级虽然没变,但等级却由偏向Ⅰ级安全标准化转变为偏向Ⅲ级安全标准化。其中j*随指标x6、x12的评分值的变化而变化的程度较大,在-30%点就已经大于2.5,使得偏向等级发生改变。
对表 6中的标准差数据进行排序,确定各指标敏感性程度量化后的相对大小,其中指标x12的2项标准差均为最大。综合上述分析,可得出权重和等级变量特征值的随指标值变化而变化的规律,并确定指标x12是对该矿山安全标准化评价结果有重大影响的敏感性指标。
3 结论1)将变权理论和物元可拓理论相结合,构建非煤矿山安全标准化评价的变权物元可拓模型。运用变权理论确定指标权重,减小了评价结果的主观性同时体现了评价指标在评价中的主动参与;采用贴近度准则代替最大隶属度准则,能有效避免传统物元可拓模型在评判过程中损失信息造成结果偏差的问题。
2)运用该模型对某非煤矿山的安全标准化体系进行评价,得出该矿山的安全标准化等级为Ⅱ级且偏向于Ⅰ级,评价结果准确合理。同时通过敏感性分析,得出“生产工艺系统安全管理”是影响该矿山安全标准化评价结果的敏感性指标。
3)变权物元可拓模型能够合理的解决非煤矿山安全标准化评价过程中的不确定问题,并得出准确性高的评判结果,为安全标准化等级评价提供了一种可靠有效的新方法。
| [1] |
周建新, 张兴凯, 刘晓宇, 等. 非煤矿山安全标准化在安全生产中的地位和作用[J].
金属矿山, 2007(4): 1–5.
|
| [2] |
赵艳艳, 李畅. 矿山安全标准化与职业健康安全管理体系的整合研究[J].
矿业研究与开发, 2015, 35(5): 78–81.
|
| [3] |
陈谨, 付俊江, 隋阳. 基于PDCA理论创建矿山安全标准化系统的研究[J].
中国安全科学学报, 2010, 20(4): 49–54.
DOI: 10.3969/j.issn.1003-3033.2010.04.008.
|
| [4] |
陈璐, 史秀志, 陈沅江. 基于成熟度模型的金属非金属矿山安全标准化体系评估研究[J].
安全与环境学报, 2013, 13(1): 224–228.
DOI: 10.3969/j.issn.1009-6094.2013.01.049.
|
| [5] |
贾明涛, 邓艳芳, 冯军. 基于信息融合的矿山安全标准化执行系统研究[J].
中国安全生产科学技术, 2017, 13(2): 62–67.
|
| [6] |
林璐瑶, 赵怡晴, 李仲学, 等. 金属非金属矿山安全标准化管理信息系统研发[J].
中国安全生产科学技术, 2012, 8(11): 178–182.
|
| [7] |
LIU Y J, TIAN Z C, HAN M, et al. Discussion on application of PDCA theory in metal and non-metal mine safety standardization management system[J].
Applied Mechanics and Materials, 2013: 2546. |
| [8] |
陈亮, 邬长福, 陈祖云, 等. 基于AHP-模糊综合评价法的非煤露天矿山安全标准化复评体系研究[J].
矿业研究与开发, 2016, 36(4): 99–103.
|
| [9] |
伍聂修, 马小明. 基于FAHP的危化品企业安全标准化评价体系研究[J].
中国安全生产科学技术, 2012, 8(1): 133–138.
|
| [10] |
张芳燕, 史秀志, 陈沅江. 基于未确知测度模型的非煤矿山安全标准化运行状况评价[J].
中国安全科学学报, 2012, 22(8): 144–149.
|
| [11] |
杨超, 史秀志. 基于Fisher判别法模型的矿山安全标准化等级评价[J].
黄金科学技术, 2018, 26(2): 187–194.
|
| [12] |
邓书显, 张学凌, 饶明贵. 基于Fuzzy逻辑和物元分析的矿井突水预测研究[J].
江西理工大学学报, 2009, 30(4): 1–3.
|
| [13] |
陈国芳, 于兆绚, 周盼. 改进物元可拓模型在采空区安全性评价中的应用[J].
有色金属科学与工程, 2015, 6(4): 91–96.
|
| [14] |
李希建, 华攸金, 陈刘瑜. 基于熵权物元可拓模型的煤矿安全评价及其应用[J].
矿业研究与开发, 2019, 39(9): 93–99.
|
| [15] |
刘映尚, 陶文伟, 周凯, 等. 基于变权物元可拓模型的二次设备状态综合评价[J].
电力系统保护与控制, 2017, 45(8): 80–85.
|
| [16] |
SONG Y, YANG H W, XU N, et al. Power system risk research based on entropy weight matter element extension model[C]//IOP Conference Series: Earth and Environmental Science. IOP Publishing, 2019, 242(2): 022005.
|
| [17] |
吴贤国, 沈梅芳, 覃亚伟, 等. 基于变权和物元原理的地铁基坑施工安全风险评价[J].
武汉大学学报(工学版), 2016, 49(6): 879–885.
|
| [18] |
柯愈贤, 王新民, 刘奇, 等. 基于熵权和物元分析的矿山安全避险"六大系统"可靠性评价[J].
黄金科学技术, 2018, 26(1): 31–39.
|
| [19] |
尹彬, 陆卫东, 贾宝山, 等. 岩爆危险性评价的变权物元可拓模型[J].
金属矿山, 2017(5): 54–59.
DOI: 10.3969/j.issn.1001-1250.2017.05.011.
|
| [20] |
王洪德, 曹英浩. 基于改进变权物元可拓模型的围岩稳定性评价[J].
中国安全科学学报, 2013, 23(8): 23–29.
DOI: 10.3969/j.issn.1003-3033.2013.08.004.
|
| [21] |
汪培庄.
模糊集与随机集落影[M]. 北京: 北京师范大学出版社, 1985: 47-59.
|
| [22] |
YAN Q Y, ZHANG M J, LI W, et al. Risk assessment of new energy vehicle supply chain based on variable weight theory and cloud model: a case study in china[J].
Sustainability, 2020, 12(8): 3150. DOI: 10.3390/su12083150. |
| [23] |
李洪兴. 因素空间理论与知识表示的数学框架(Ⅷ)[J].
模糊系统与数学, 1995(3): 1–9.
|
| [24] |
张晓平. 基于贴近度的模糊综合评判结果的集化[J].
山东大学学报(理学版), 2004(2): 25–29.
DOI: 10.3969/j.issn.1671-9352.2004.02.006.
|
| [25] |
全国安全生产标准化技术委员会. AQ 2007.1-2006, 金属非金属矿山安全标准化规范导则[S]. 北京: 中国安全生产科学研究院.
|
 2021, Vol. 12
2021, Vol. 12


