| 基于EW-AHP和未确知测度理论的隧道瓦斯风险评价 |
b. 江西理工大学,江西省矿业工程重点实验室,江西 赣州 341000
b. Jiangxi Provincial Key Laboratory of Mining Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, Jiangxi, China
近年来,随着国家对基础建设的大力投入,我国隧道工程建设得到快速发展,不仅数量多、长度长,而且施工技术也得到了前所未有的发展,许多施工方法的应用不断取得突破[1-2]。在隧道建设过程中,地质条件相比早年会更加复杂,往往会穿越含瓦斯地层,瓦斯突出或爆炸引发的灾害不仅对设备设施、施工场所破坏严重,而且会给施工人员带来生命危险,给国家造成巨大损失[3-5]。在勘探设计阶段对隧道瓦斯风险进行评估,并在施工阶段采取有针对性的防范措施可有效减少其带来的危害。因此,对隧道瓦斯风险进行评价已成为隧道建设中不可缺少的一个环节。
近年来,许多学者用不同方法对隧道瓦斯风险评价进行了研究,主要有层次分析法[6-8]、蒙德法[9]、FDA法[10]、物元可拓理论[11]等。虽然这些方法都取得了较好的成果,但由于隧道瓦斯风险评价受模糊性和可变性等因素所控制,且因素之间往往会相互影响,从而增大了评价过程的复杂性和不确定性,使得上述研究方法都具有一定的局限性。针对隧道瓦斯风险评价中的问题,为了提高评价模型的准确度,基于熵权法和层次分析法组合赋权的未确知测度理论能够为其提供合理可行的解决途径。
未确知测度理论是一种能够有效解决评价对象不确定性问题的研究方法,广泛应用于各类工程领域的综合评价问题中[12-16]。其总体思路是通过建立各评价指标评判体系并划分评价等级,将所有评价指标定量化后进行赋权,再以权重数值来确定最终评价结果[17-19]。传统未确知测度模型通常是运用熵权法或简单的关联函数来确定权重,再采取最大隶属度准则来进行等级评定[20]。然而通过熵权法来确定指标权重会使得权重受样本数据变化影响较大,而且由于缺乏经验指导,最终结果往往会忽视决策者的主观意图;由于评价体系具有有序性,最大隶属度准则有着在某些情况下无法反映评价对象自身界限的模糊性和易丢失评价信息的缺陷[21]。为弥补这些不足和缺陷,本文将熵权法和层次分析法相结合,对传统的赋权方法进行改进。首先,运用未确知测度理论确定各评价指标的测度评价矩阵;其次,将2种方法确定的权值通过乘法合成归一化法进行耦合,确定指标综合权重;最后,采用置信度识别准则来代替最大隶属度准则,根据多指标测度向量确定评价等级。由此构建隧道瓦斯风险评价模型,基于此模型对隧道瓦斯风险进行评价,从而获得相对准确的评价结果,可为预防和控制隧道瓦斯风险提供参考。
1 隧道瓦斯风险未确知测度评价模型假设评价指标空间A有m个评价对象,即评价指标空间A={a1,a2,…,am},使每个评价对象ai(i=1,2,…,m)都有n个单项评价指标qi(i=1,2,…,n)与其对应,则构造ai的n维向量,即ai={ai1,ai2,…,ain}。其中:aij(i=1,2,…,m;j=1,2,…,n)表示隧道瓦斯风险评价指标的测度值。设各对象被划分为t个评价等级,评价等级空间D={C1,C2,…,Ct},若θ级评价等级高于θ+1级评价等级,即Cθ > Cθ+1,则称{C1,C2,…,Ct}为评价等级空间D上的一个有序分割类。
1.1 单指标未确知测度设αijθ=α(aij∈Cθ)表示测度值aij为第θ个评级等级Cθ的隶属度,并且α满足以下要求:
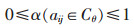
|
(1) |
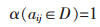
|
(2) |
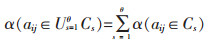
|
(3) |
(i=1,2,…,m;j=1,2,…,n;s=1,2,…,θ;θ=1,2,…,t)
其中,式(1)表示未确知测度的“非负有界性”;式(2)表示未确知测度满足“归一性”;式(3)表示“可加性”。
按下列方法构造隧道瓦斯风险评价单指标测度函数α(aij∈Cθ):当aij≤xj1时,aijt取值为1,其余测度值取值为0;当aij≥xjt时,aijt取值为1,其余测度值取值为0,其中xjv(v=1,2,…,θ)表示分级标准的临界值;当xj1≤aij≤xjt时,根据未确知测度的定义,由构造的线性函数来确定评价指标测度值。求得各评价对象ai的测度值aijθ,根据各对象测度值构造的单指标测度评价矩阵如下:
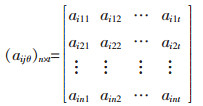
|
(4) |
熵体现研究对象的随机性和无序程度,从而反应评价指标的重要性,熵值越小,无序化程度越小。熵权法是根据评价指标值构造的判断矩阵来确定权重,可以减小主观因素对评价指标权重的影响,使评价指标的权重更好的体现各指标对综合未确知测度所起的作用。假设评价指标qj同其他指标相比的重要度表示为βij(0≤βij≤1,βij=1),则评价指标qj的权值为βij,其他评价指标权值可同理求出,熵值计算如下:
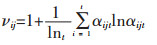
|
(5) |
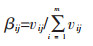
|
(6) |
对影响隧道瓦斯风险的各个因素进行划分,将其分为最高层、中间层和最底层,层与层之间相互关联,把每一层的指标通过9级标度法进行一一对比,分为1~9个标度,标度1代表 2个因素有相同重要度,标度9代表 2个因素相比极端重要,用此方法构建每一层指标的判断矩阵,即A=(aij)n×n;运用方根法对判断矩阵进行计算,得到每层各因素的权重近似值,公式如下:

|
(7) |
对其进行归一化处理后,得到各因素相对于最高层的权重值;最后对每一层的判断矩阵进行一致性检验,若随机一致性比率CR < 0.1时,则各因素的层次划分是合理的;若没有满足此条件,需要对层次分析排序进行调整,再次计算。
1.2.3 乘法归一化方法确定指标综合权重将熵权法确定的客观权重和层次分析法确定的主观权重运用乘法归一化方法进行耦合,得出综合权重,可以弥补数据过少和主观性太强的缺陷,计算公式如下:
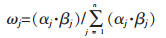
|
(8) |
式(8)中:ωj是第j个指标的综合权重;αj是第j个指标的主观权重;βj是第j个指标的客观权重;n为评价指标的数量。
1.3 多指标综合测度根据组合赋权得出的评价指标综合权重求出各因素的多指标综合测度,令αiθ=α(ai∈Cθ)表示评价对象属于第θ个评级等级的隶属度,结合公式αiθ= 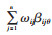
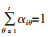
若{C1 > C2 > … > Ct}为有序时,最大隶属度原则的准确性不高,本文引入置信度识别准则[22]。设λ为置信度,一般λ的取值范围为0.5 < λ < 1.0,通常取λ=0.5或λ=0.6。置信度识别公式如下:
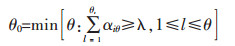
|
(9) |
若满足上述公式,则认为隧道瓦斯风险等级属于第θ0个评价等级。
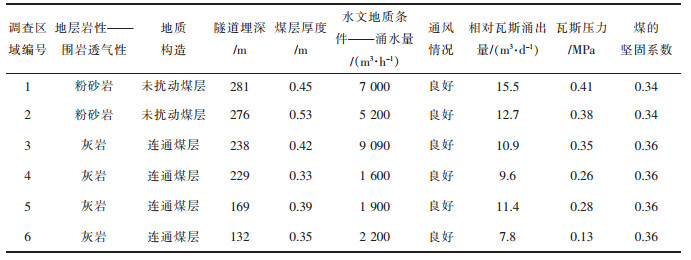
2 实例分析 2.1 研究区域隧道概况研究区域地貌呈低平山势,地形地势起伏较大,隧道总长度为4 542 m,最大埋深281 m,下伏地层基岩为石炭系下统梓山组(C1z)炭质页岩夹煤层、页岩、泥岩、砂岩。隧道穿越煤层且临近村户,易发生瓦斯灾害且灾害影响较大。本文选取隧道6个研究区域作为评价对象。
2.2 隧道瓦斯风险概率等级评价 2.2.1 隧道瓦斯风险概率等级的确定根据国内相关学者的评价等级划分标准和影响因素本身的特征对各指标进行分级,建立隧道瓦斯风险概率评价等级Z={z1,z2,z3,z4},其中,z1:不可能;z2:偶尔;z3:可能;z4:很可能。
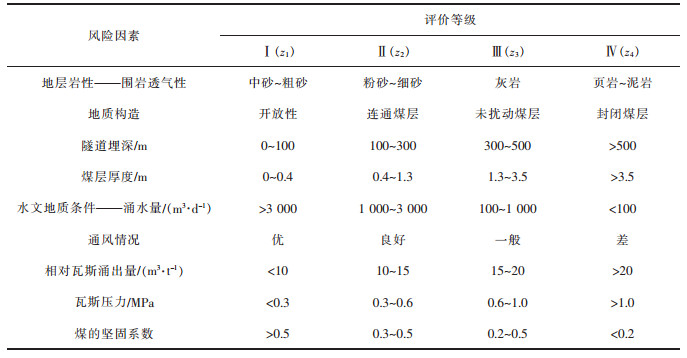
2.2.2 隧道瓦斯风险评价指标的选取隧道瓦斯风险评价指标的选取需要考虑众多因素,指标的选取不仅要考虑造成瓦斯突出、爆炸、窒息等风险的主要因素,保证评价结果的准确性,也要考虑在隧道工程建设中相关因素的获取情况,保证评价结果的可操作性。考虑上述分析,对相关规范和国内现有的研究成果进行归纳[23-25],并总结高杨等对铁路瓦斯隧道分类分级标准的探讨[26],本文最后确定了9个评价指标,包括3个定性的评价指标和6个定量的评价指标,即:地层岩性(围岩透气性)、地质构造、隧道埋深、煤层厚度、水文地质条件(涌水量)、通风情况、相对瓦斯涌出量、瓦斯压力、煤的坚固系数。各指标分级判断标准和隧道不同区域各指标的调查统计数据见表 1和表 2。部分评价指标的说明如下:
| 表 1 隧道瓦斯风险评价指标分级判断标准 Table 1 Classification criteria of tunnel gas risk assessment index |
 |
| 点击放大 |
| 表 2 隧道瓦斯风险评价指标调查统计 Table 2 Investigation and statistics of tunnel gas risk assessment index |
 |
| 点击放大 |
1)地层岩性:地层岩性即围岩的透气性决定了瓦斯赋存或者逸散的难易程度,一般来说,围岩的透气性越好,瓦斯越容易逸散;反之,则越容易赋存。
2)地质构造:地质构造是瓦斯赋存的场所或者逸散的渠道,地质构造的规律、性质以及构造线和隧道轴线的相交或相切形式对于隧道瓦斯风险有着不可分割的作用。
3)隧道埋深:隧道埋深对于瓦斯压力的积存有积极作用。隧道的埋深越深对瓦斯压力的积存越有利,当瓦斯压力到达一定数值后,就易发生瓦斯突出等事故。
4)水文地质条件(涌水量):水文地质条件相关因素有许多,本文只考虑对瓦斯风险最主要的影响因素,即涌水量。地下水流出涌动时会带走一部分瓦斯气体,涌水量越大,隧道内瓦斯越少。
5)相对瓦斯涌出量:相对瓦斯涌出量的多少从一定程度上反映了隧道内瓦斯的赋存情况,在相同的施工情况下,相对瓦斯涌出量大的区域其瓦斯含量也相对较大,易导致瓦斯压力过高,引发瓦斯突出等危险。
2.2.3 单指标测度函数隧道瓦斯风险各评价指标的单指标测度函数如图 1所示,其中地层岩性、地质构造、通风情况3个指标的测度函数为单位指标取值函数,如图 1(g)所示。本文以1号调查区域为例,根据其各指标调查的数据,结合各指标的测度函数,构造出1号调查区域的单指标评价矩阵,如下所示:

|
(10) |
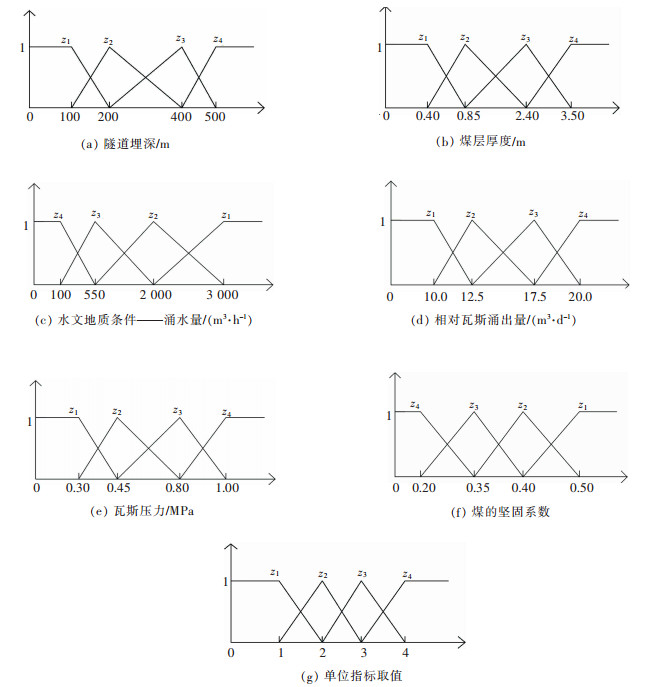 |
| 图 1 隧道瓦斯风险单指标测度函数 Fig. 1 Single index measurement function of tunnel gas risk |
2.2.4 EW法和AHP法组合赋权
将EW法计算所得的客观权重与AHP法计算所得的主观权重通过乘法合成归一的方法进行耦合,按照式(8)来计算各指标的综合权重,进行组合赋权。以1号调查区域为例,计算步骤如下:
1)EW法赋权:EW法的基本思路是根据评价指标变异性的大小来确定客观权重,指标值的变异程度越大,能够提供的信息量越多,所需的信息量越少,在评价中起的作用就越大,权重就越大。反之,权重就越小。根据评价矩阵式(10),按式(5)和式(6)计算,得出各评价指标的客观权重。
2)AHP法赋权:根据2.2.2节的分析,构建了隧道瓦斯风险评价结构模型,模型中分为3个层级,首先最高层A为隧道瓦斯风险评价的目标;其次为中间层B,分为隧道地质条件、瓦斯情况、其他因素,隧道地质条件包括地层岩性、地质构造、水文地质条件、隧道埋深、煤层厚度,瓦斯情况包括相对瓦斯涌出量、瓦斯压力、煤的坚固性系数,其他因素包括通风情况;最后为最底层C,包括上述9个评价指标。专家按照9级标度法对中间层和最底层中的各个指标进行一一对比,根据重要性构建两层级的判断矩阵,按照式(7)计算近似权重值,归一化处理后,得到中间层B各因素的权重为{0.236,0.682,0.082}。最底层C各评价指标的权重。
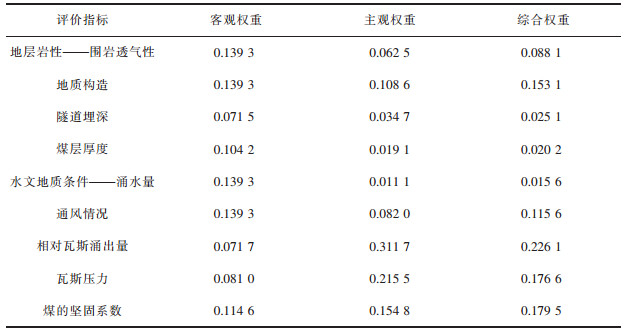
3)组合赋权:将EW法计算所得的客观权重与AHP法计算所得的主观权重通过乘法合成归一的方法进行耦合,按式(8)把表 3中的客观权重与主观权重耦合,得出各评价指标的综合权重。
| 表 3 评价指标综合权重值 Table 3 Comprehensive weight value of evaluation index |
 |
| 点击放大 |
评价指标各权重值见表 3。
2.2.5 多指标综合测度评价向量由上述计算可得出1号调查区域的综合权重和测度评价矩阵,将两者相乘可得出1号调查区域的多指标综合测度评价向量,向量为{0.080 7,0.440 8,0.466 4,0.012 0}。同理,可求得其他调查区域的多指标综合测度评价向量。此外,将各调查区域的客观权重和测度评价矩阵相乘得出的多指标综合测度评价向量来作为对比。
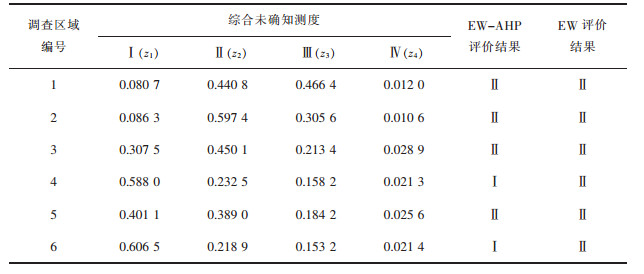
2.2.6 置信度识别由于评价体系具有有序性,本文采用置信度识别准则。取λ=0.5,θ0=z1+z2=0.521 5 > 0.5,可得出1号调查区域的瓦斯风险可能性等级为Ⅱ级。同理可求得其他调查区域的瓦斯风险可能性等级,见表 4。
| 表 4 隧道瓦斯风险评价结果 Table 4 Tunnel gas risk assessment results |
 |
| 点击放大 |
2.3 评价结果分析
对评价结果分析发现,1、2、3、5号调查区域的瓦斯风险可能性等级为Ⅱ级,4、6号调查区域的瓦斯风险可能性等级为Ⅰ级。评价结果与现场施工实际情况高度吻合。但是对比EW-AHP法和传统EW法的评定结果发现,有2个样本的评定结果存在差异。造成结果有差异的主要原因有2方面,一方面是在实际的数据采集过程中,往往存在一些瑕疵,并非完美的数据,这会导致在数据计算过程中差异化被放大;另一方面是EW法本身就存在一些缺陷,EW法不够智能化,首先,没有考虑到各个评价指标间的相互影响,忽略了评价指标本身的重要度,可能存在确定的评价指标权数和期望的结果有较大偏差,其次,对样本有较大的依赖性,模型样本的不断变化会导致权重发生一些波动,若指标值变化很微小或剧烈变化,用EW法赋权就存在一定的局限性。EW法遵循数学规律,具有严格的数学意义,但没有考虑决策者的主观意图,缺乏经验指导,其得出的权重可能会失真。EW-AHP法可以将主观和客观的赋权方法相结合,弥补EW法存在的部分缺陷,发挥2种方法赋权的优势,使评价结果更加合理和贴近实际的情况。所以,用EW-AHP法赋权的评价模型具有一定的准确性和可行性,可作为类似隧道项目施工中的瓦斯风险有效评价模型。
3 结论本文综合考虑了有关规范和前人研究成果,选取了数据相对易获取的9个评价指标,这些评价指标在实际情况中具有较高的适用性和可操作性。以此构建了隧道瓦斯风险评价体系,并划分了隧道瓦斯风险可能性等级。
将EW法赋权和AHP法赋权相结合,通过组合赋权确定了评价指标的综合权重,构建基于未确知测度理论的隧道瓦斯风险评价模型。此评价模型既保证了客观赋权的高可信度和精确度,也较好的弥补了无经验指导的缺陷;采用置信度识别准则代替最大隶属度准则,能有效避免传统评价模型在评判过程中损失信息造成结果偏差的问题。
利用此评价模型对隧道瓦斯风险进行评价,评价结果相对于传统方法的评价结果更贴近实际施工情况,此模型的评价结果准确性高,也可作为类似隧道施工中的瓦斯风险有效评估模型。
| [1] |
王梦恕. 中国铁路、隧道与地下空间发展概况[J].
隧道建设, 2010, 30(4): 351–364.
|
| [2] |
赵勇, 田四明, 孙毅. 中国高速铁路隧道的发展及规划[J].
隧道建设, 2017, 37(1): 11–17.
|
| [3] |
汪跃飞. 黄草隧道高瓦斯施工通风及风险防控应用研究[J].
科技与创新, 2020(23): 51–53.
|
| [4] |
陈鹏. 瓦斯隧道施工危险性评价研究[J].
黑龙江交通科技, 2020, 43(7): 165–166.
DOI: 10.3969/j.issn.1008-3383.2020.07.101.
|
| [5] |
陆瑜. 含煤公路隧道施工瓦斯突出安全风险评估[J].
路基工程, 2019(6): 218–222.
|
| [6] |
张艳涛, 朱宝合, 高强, 等. 基于AHP的公路瓦斯隧道施工风险影响因素分析[J].
采矿技术, 2020, 20(1): 115–118.
DOI: 10.3969/j.issn.1671-2900.2020.01.033.
|
| [7] |
陈飞, 郭顺, 熊如宗, 等. 基于层次分析法的地质灾害危险性评价研究[J].
有色金属科学与工程, 2018, 9(5): 54–60.
|
| [8] |
HOSCAN O, CETINYOKUS S. Determination of emergency assembly point for industrial accidents with AHP analysis[J].
Journal of Loss Prevention in the Process Industries, 2021, 69(prepublish): 104386. |
| [9] |
蒋晓槟, 李博, 薛亚东. 基于蒙德法的穿煤层隧道瓦斯风险评估[J].
地下空间与工程学报, 2012, 8(6): 1292–1295.
|
| [10] |
熊建明, 陈沅江, 刘波, 等. 瓦斯隧道施工期风险等级的FDA法评价[J].
重庆交通大学学报(自然科学版), 2017, 36(2): 17–23.
|
| [11] |
黄仁东, 张小军. 基于熵权物元可拓模型的隧道瓦斯等级评价[J].
中国安全科学学报, 2012, 22(4): 77–82.
DOI: 10.3969/j.issn.1003-3033.2012.04.014.
|
| [12] |
张贤平, 杨斌清, 向燕. 基于未确知测度模型的稀土原地浸矿地下水污染风险评价[J].
有色金属科学与工程, 2018, 9(6): 81–88.
|
| [13] |
翟强, 顾伟红. 基于EW-AHP和未确知测度理论的隧道坍塌风险评价[J].
安全与环境工程, 2020, 27(5): 92–97.
|
| [14] |
苏生瑞, 周阳, 周泽华, 等. 基于EW-AHP和未确知测度理论的崩塌危险性评价[J].
工程地质学报, 2019, 27(3): 577–584.
|
| [15] |
KAUFMANN M, EFFENBERGER I, HUBER M F. Measurement uncertainty assessment for virtual assembly[J].
Journal of Sensors and Sensor Systems, 2021, 10(1): 28–36. |
| [16] |
YANG L, ZHANG X Y, XU W H, et al. Multi-granulation Rough Sets and Uncertainty Measurement for Multi-source Fuzzy Information System[J].
International Journal of Fuzzy Systems, 2019, 21(5): 1919–1937. DOI: 10.1007/s40815-019-00667-1. |
| [17] |
王凤菲, 王恩茂, 徐同启. 基于组合赋权-未确知测度理论的地铁隧道围岩质量评价[J].
铁道标准设计, 2019, 63(6): 129–134.
|
| [18] |
朱玉娟, 王宏辉. 基于改进熵权-未确知测度理论的在役混凝土梁桥安全性评价[J].
价值工程, 2019, 38(30): 180–182.
|
| [19] |
FORDONI S, RASHID M. Multiple selections of kashmir tunnel risk by fuzzy multiple-criteria decision analysis[J].
Journal of Bioinformatics and Intelligent Control, 2015, 4(1): 2326–7496. |
| [20] |
李文龙, 李慧民, 孟海, 等. 基于熵权-未确知测度理论的装配式建筑施工安全风险评估[J].
西安建筑科技大学学报(自然科学版), 2019, 51(3): 369–374.
|
| [21] |
何美丽, 刘霁, 刘浪, 等. 隧道坍方风险评价的未确知测度模型及工程应用[J].
中南大学学报(自然科学版), 2012, 43(9): 3665–3671.
|
| [22] |
程乾生. 属性识别理论模型及其应用[J].
北京大学学报(自然科学版), 1997(1): 14–22.
|
| [23] |
肖鹏, 丁毅, 李树刚. 基于未确知测度的矿井瓦斯防治管理体系评价[J].
中国安全科学学报, 2017, 27(1): 98–103.
|
| [24] |
孙庆刚. 中国煤矿瓦斯灾害现状与防治对策研究[J].
中国煤炭, 2014, 40(3): 116–119.
|
| [25] |
文畅平. 隧道瓦斯突出危险性评价的属性识别模型与实例[J].
煤炭学报, 2011, 36(8): 1322–1328.
|
| [26] |
高杨, 杨昌宇, 郑伟. 铁路瓦斯隧道分类分级标准探讨[J].
隧道建设, 2017, 37(11): 1366–1372.
DOI: 10.3973/j.issn.2096-4498.2017.11.002.
|
 2021, Vol. 12
2021, Vol. 12


