| 不同含水率红砂岩冲击过程中的能量耗散特性 |
地下岩体工程普遍遭受地下水困扰,致使各类地下岩石工程灾害的发生,例如:地下水的渗漏可能导致岩溶塌陷[1],断层活化[2]和影响采空区稳定性[3]等。由于地下水位的升降等原因,工程岩体中的含水率具有动态变化特性。当岩体受到地震和爆破等动荷载影响时,不同含水率岩石的动态响应也将不同,这对保证地下岩石工程的稳定性提出了挑战[4-5]。为此,研究含水率对岩石动力学特性的影响具有重要的理论和工程实际意义。
王斌等对自然风干和饱水状态下的开阳磷矿砂岩进行了静态、中应变率和动态加载试验,结果表明饱水状态下的静态压缩强度比自然风干状态更低,两者在中等加载率下的抗压强度相近,而在高加载率下饱水红砂岩反而高于干燥状态[6]。Eunhye Kim和Hossein Changani对饱和干燥红砂岩和浅黄砂岩分别进行静态、中等应变率和高应变率加载,发现饱水状态下2种砂岩的静态和动态抗压强度相对干燥状态的对应强度下降大约20%;饱水状态的浅黄砂岩杨氏模量低于干燥状态,而饱水状态和干燥状态红砂岩的杨氏模量变化不明显[7]。王浩宇等研究干燥砂岩试样、自然砂岩试样、吸水砂岩试样和饱水砂岩试样的静态和动态抗压强度,并以电镜扫描技术分析了砂岩破坏的微观机制,结果表明,砂岩静态和动态抗压强度均随含水率增加而降低,并提出干燥砂岩试样破裂时矿物颗粒被剪断,而饱水砂岩的破坏主要由矿物边界破坏引起,由于矿物颗粒强度较矿物边界破裂强度更高,导致干燥砂岩试样强度高于饱水砂岩试样[8]。李天斌等对不同含水率砂岩在静态三轴加载过程中的能量演化特征进行研究,结果表明含水率的增大导致了砂岩总吸收能减少,随时间的增速减缓;弹性能积蓄加快;总耗散能减少[9]。Aihong Lu等对6组不同含水率砂岩进行冲击试验,研究发现随着含水率从0增加到2.58%,砂岩的强度、动态弹性模量和卸载模量均减小,并通过分析应力波所携带的能量发现随着含水率的增加,反射波能量增大,而透射波能量和岩石损伤耗散的总能量均减小[10]。
当前关于岩石动态响应的研究主要集中在探究水对岩石强度、变形特征以及破坏时总耗散能的影响,而研究含水率对岩石承受动载时能量演化过程的影响报道较少,这不利于分析冲击加载过程中岩石的变形损伤过程及机理。Wang Peng等通过红砂岩的应力应变曲线及弹性模量计算了单次冲击过程中,不同应变率和冻融循环次数下红砂岩的能量和损伤演化,分析不同应变率下冻融循环次数对红砂岩能量耗散特征和损伤演化的影响,并取得了较好的成果[11]。因此,本文通过对干燥状态、自然含水状态、自然饱水状态和强制饱水状态4种不同含水状态的红砂岩进行冲击试验,引进由应力应变曲线和杨氏模量计算单次冲击过程中能量演化的计算方法,计算不同含水率红砂岩的能量-时间演化曲线和能量-应变演化曲线。基于不同含水率红砂岩冲击过程中的能量-时间演化曲线特性,划分红砂岩能量演化过程的不同阶段。研究各能量演化阶段的持续时间,以及各能量演化阶段起点,包括弹性变形起点、岩石起裂点、宏观破坏发生点的起始时间与含水率的关系。基于能量-应变演化曲线,研究含水率对红砂岩达到各能量演化阶段时累积变形的影响,并通过砂岩破坏(卸载)时耗散能占总应变能的比例,探究不同含水率红砂岩累积塑性变形的能力。由能量-时间演化曲线和能量-应变演化曲线中的耗散能定义岩石冲击过程中的损伤变量,分析红砂岩的损伤-时间和损伤-应变演化关系,探索含水率对红砂岩冲击过程中损伤演化的影响。
1 试验方案和分析方法 1.1 岩石试件及含水率设计选用红砂岩制备岩石试件,试件尺寸为Ф50 mm×50 mm,试件端面不平整度<±0.02 mm。试验中对红砂岩分别设置了4种含水状态:干燥状态、自然吸水状态、自然饱水状态和强制饱水状态,并通过精确度为0.01 g的电子天平测算岩石质量的变化来计算红砂岩的含水率[12]:

|
(1) |
式(1)中:ω是红砂岩的含水率;mw是含水砂岩的质量;md是干燥状态砂岩的质量。
为了获得干燥状态的红砂岩,将打磨好的红砂岩置于温度为110 ℃的烘箱中烘干24 h,此后红砂岩质量几乎不再减小,可以认为红砂岩已经达到干燥状态[12]。将部分干燥砂岩置于底部有支架的密闭容器中,随后在容器中加水并保证试件与水没有接触,期间湿度计测得容器中湿度约为70%,每24 h取出称量质量,当试件连续3次称量质量不变时,则认为试件含水率达到了最大值,此时的含水率为自然含水状态下的含水率。
制备自然饱水状态红砂岩时,将试件置于容器中,注水浸没试件至高出试件顶端2 cm左右。与制备自然含水状态砂岩相同,每24 h取出称量质量,当试件连续3次称量质量不变时,认为红砂岩达到了自然饱水状态。而制备强制饱水状态红砂岩时,将试件置于盛水容器中并抽真空至真空负压力为0.08 MPa,放置72 h后视为达到强制饱水状态[13]。
图 1展示了制备自然含水状态、自然饱水状态和强制饱水状态下砂岩试件的示意图。吸水试验显示出,自然含水状态下砂岩试件含水率约为1.0%,自然饱水状态下砂岩试件含水率约为3.0%,而强制饱水状态下砂岩试件含水率约为3.6%。
 |
| 图 1 制备不同含水率砂岩试件的示意 Fig. 1 Schematic diagram of prepare red sandstone specimen with different water content |
1.2 试验装置
采用霍布金逊压杆(Split Hopkinson Pressure Bar, SHPB)对不同含水状态的红砂岩进行动态冲击试验,示意图如图 2所示,由入射杆、透射杆和吸收杆组成,杆件直径为50 mm,杆件系统及冲头材质均为高强度40 Cr合金钢,其密度为7 800 kg/m3,纵波波速为5 400 m/s,弹性模量为250 GPa。为减小PC振荡,冲头选用长度为265 mm的纺锤形冲头,尺寸示意图如图 3所示。
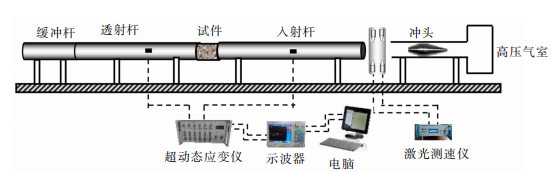 |
| 图 2 霍布金逊压杆系统 Fig. 2 Split Hopkinson pressure bar system |
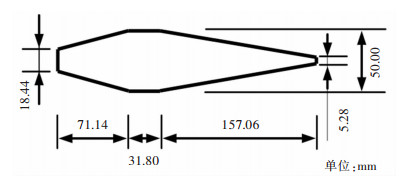 |
| 图 3 纺锤形冲头尺寸 Fig. 3 Cone-shaped striker dimensions |
1.3 试验方法
在每次冲击试验的准备阶段,固定冲头在腔膛中的初始位置,并保持高压气室中的气压为0.6 MPa。测试过程中,试件两端涂抹黄油以减少端部效应,然后将试件夹在入射杆和透射杆之间,其轴线与杆件系统尽量重合,随后打开高压气室将冲头击出,速度值约为16 m/s。为保证试验结果的可靠性,每种含水率制备3个岩样,共12个红砂岩试样进行冲击加载试验。根据贴在入射杆和透射杆上的应变片采集到的应力波信号,通过三波法可以得到红砂岩在动态加载过程中的应力应变曲线[14]。
1.4 单次冲击变形过程中能量计算方法忽略动态加载过程中红砂岩与外界的能量交换,且只考虑岩石的轴向应力和应变,在主应力空间中红砂岩单元的总输入应变能、可释放弹性应变能和耗散能可以表示为[15]:

|
(2) |
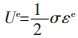
|
(3) |
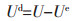
|
(4) |
式(2)、式(3)、式(4)中:U、Ue和Ud分别为红砂岩单元的总应变能、可释放弹性应变能和耗散能;σ为红砂岩的动态压缩应力;ε为红砂岩的总应变;εe为红砂岩的弹性应变。
根据三波法计算得到的应力应变曲线以及式(2)~式(4),红砂岩的能量演化曲线可以被准确地计算出来。通过应力应变曲线各点计算单位体积总应变能、可释放弹性应变能和耗散能的示意图见图 4。为了便于计算,以应力应变曲线起点与50%峰值应力点的割线斜率来近似地作为红砂岩的卸载模量[16-17],可释放弹性应变能的表达式可以改写为:

|
(5) |
 |
| 图 4 岩石单元的可释放弹性应变能和耗散能 Fig. 4 Dissipated energy and releasable elastic strain energy of a rock unit |
2 试验结果
图 5所示为不同含水率红砂岩在16 m/s冲击速度下得到的入射波、反射波和透射波。由图 5可以看出,在相同的入射波工况下,随着岩石含水率的增加,反射波幅值逐渐增加,透射波幅值逐渐减小。由一维应力波理论可知,这是由于随着含水率的递增,岩石试件的波阻抗逐渐减小导致的。
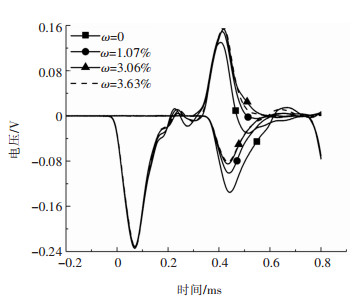 |
| 图 5 不同含水率红砂岩冲击试验得到的入射波、反射波和透射波 Fig. 5 Incident wave, reflected wave and transmitted wave obtained from impact test of red sandstone with different water content |
2.1 动态应力应变曲线
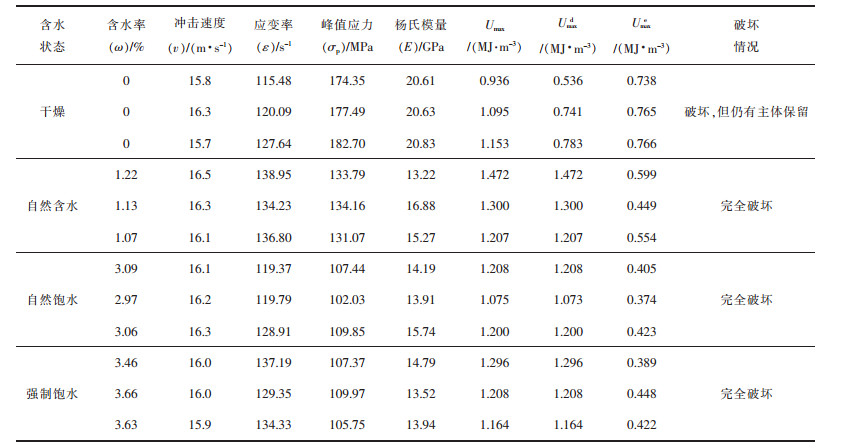
根据图 5的波形试验结果,结合SHPB的试验原理,可以得到不同含水率工况下岩石的动态应力-应变曲线,如图 6所示,红砂岩冲击试验的动态响应参数结果如表 1所列。
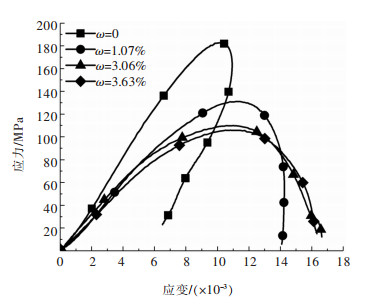 |
| 图 6 不同含水率下红砂岩的动态应力-应变曲线 Fig. 6 Dynamic stress-strain curve of red sandstone with different water content |
| 表 1 红砂岩冲击试验结果 Table 1 SHPB test results |
 |
| 点击放大 |
由图 6可以看出,在相同的冲击载荷作用下,不同含水率红砂岩的动态应力-应变曲线形状不同。随着含水率的增加,动态峰值应力逐渐减小,体现出水对岩石动态强度的弱化效应。当含水率为零时,在冲击速度为16 m/s的动载荷作用下,红砂岩的动态应力随着动态应变的增加而增加,当达到最大峰值应力后,由于岩石试件仍有具有承载能力的主体保留,应力-应变曲线存在一个卸载阶段,即积聚在岩石试件中的弹性应变能逐渐释放到外界,此时的应力-应变曲线为Ⅱ型曲线[18]。当含水率ω=1.07%、3.06%和3.63%时,在冲击速度为16 m/s的动载荷作用下,红砂岩完全破坏,不再有主体保留,应力-应变曲线不再具有卸载阶段,变成了所谓的Ⅰ型曲线,Ⅰ型和Ⅱ型应力应变曲线所对应的典型破坏情况如图 7所示。另外,随着含水率的增加,岩石的最大动态应变越来越大,体现出含水率的增加有利于岩石延性性能的提升。
 |
| 图 7 Ⅰ型和Ⅱ型应力应变曲线所对应的典型破坏情况 Fig. 7 Typical failure behavior corresponding to the classⅠand class Ⅱ stress-strain curves |
2.2 动态杨氏模量与含水率的关系
岩石的动态杨氏模量可以表征岩石在动载荷作用下抵抗变形的能力,也是利用式(3)中确定岩石可释放弹性应变能的重要参数。根据图 6所示的动态应力-应变曲线,连接其起点与50%峰值应力点,得到的割线斜率作为红砂岩的杨氏模量[19],结果如表 1所示。不同含水率工况下红砂岩动态杨氏模量如图 8所列,由图 8可以看出,随着含水率的增加,红砂岩的杨氏模量先快速减小后逐渐趋于稳定;其中自然含水状态下红砂岩杨氏模量较干燥状态下降约30.5%,而强制饱和状态下杨氏模量平均值与自然饱和状态变化不大。这表明,当含水率较低时,含水率的变化对岩石动态杨氏模量有较大的影响,而当红砂岩接近饱和状态时,含水率的变化对红砂岩动态杨氏模量的影响可以忽略不计。红砂岩动态杨氏模量与含水率之间呈现良好的指数关系,

|
(6) |
 |
| 图 8 杨氏模量与含水率的关系 Fig. 8 Relationship between the Young's modulus and water content |
分析认为,红砂岩动态杨氏模量随含水率的增加而减小,并在接近饱和时趋于稳定主要有2个原因,一是水与岩石中的钠长石等矿物发生化学反应使红砂岩发生了溶蚀[20],以及初始裂隙中的水与砂岩中的伊利石等黏土矿物混合发生了膨胀[21],导致初始裂隙的进一步发育,这些机理使红砂岩在还未进行动态加载时已经产生了初始损伤。当含水率较低时,大部分矿物已经与水完成反应。因此在高含水率下,矿物与水反应造成的初始损伤难以随含水率的增加进一步提高。二是含水率较低时,水分子与矿物颗粒表面的电荷结合形成结合水,其形成的结合水膜会导致岩石骨架凝聚力和摩擦力的减小。当砂岩试件承受动载时,裂隙更容易扩展、成核,岩石的强度和抗变形能力降低。而当含水率较高时,结合水以外的大部分水分子作为自由水在岩石中流动,由于自由水与矿物颗粒距离较远,无法形成弱化机制,对岩石骨架的影响比较微弱,因此含水率继续增加对于岩石骨架摩擦力和凝聚力的减小有限[22]。
3 冲击过程中砂岩的能量演化特性 3.1 能量随时间的演化特性结合图 6所示的动态应力-应变曲线和式(2)~式(5),计算不同含水率工况下红砂岩动态冲击过程中的单位体积总应变能、可释放弹性应变能和耗散能,图 9所示为3个能量随时间的变化关系。
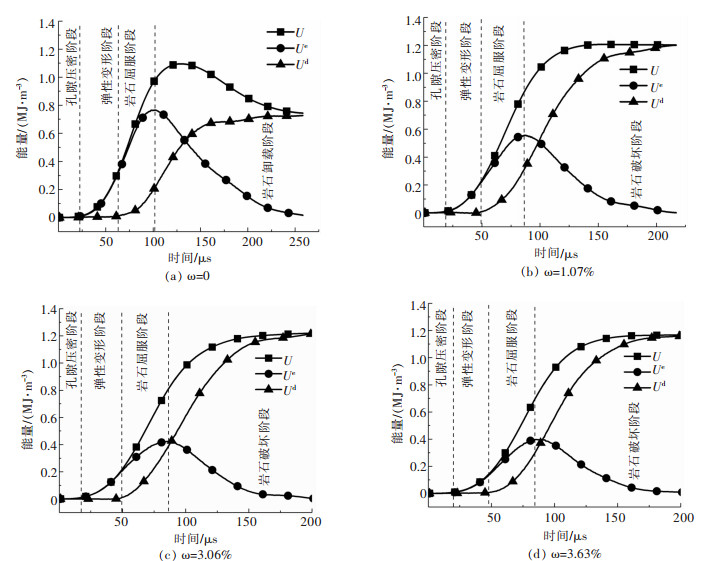 |
| 图 9 红砂岩在不同含水率下的能量-时间演化曲线 Fig. 9 Energy-time evolution curve of red sandstone with different water content |
由图 9可以看出,当红砂岩完全破坏时,其单位体积总应变能和耗散能随时间的变化趋势呈典型的“S”型,先平稳发展,然后逐渐增加,最后又趋于不变。可释放弹性应变能随时间的增加先增大后减小。红砂岩未完全破坏时,耗散能和可释放弹性应变能随时间的变化趋势与完全破坏时一致,而单位体积总应变能的变化趋势变为先平稳发展,然后逐渐增加,最后减小至与耗散能相等,这表示岩石中总应变能的一部分被释放到外界。
分析3个能量随时间演化的规律可以看出,在能量随时间演化的初期,岩石单元的总应变能、可释放弹性应变能和耗散能均增加不明显。随后,岩石单元的总应变能和可释放弹性应变能开始迅速增长,增速也逐渐变快,两者随时间的演化曲线几乎重合,但耗散能仍未发生明显增长。随着红砂岩单位体积总应变能的进一步增加,可释放弹性应变能与总应变能随时间仍然增加,但两者的演化曲线逐渐分离,耗散能开始明显增加。
可释放弹性应变能累积达到一定值后开始下降,此时总应变能和耗散能根据红砂岩是否完全破碎分为2种演化趋势:当红砂岩未完全破碎时,总应变能先增加后减小,最后趋于平缓。耗散能先增加后趋于平缓。总应变能减小后达到的最小值与耗散能的最大值相等。当红砂岩完全破碎时,总应变能和耗散能先增加然后均趋于平缓,总应变能先达到最大值,随后耗散能也达到最大值,两者所达到的最大值相等。当可释放弹性应变能下降到零时,耗散能在2种演化趋势中均达到最大值。
3.2 基于能量演化特性的裂纹起裂和破坏判定根据3种能量随时间演化的特征,红砂岩在冲击过程中的能量-时间演化可以分为4个阶段。在第1阶段,红砂岩单元的总应变能增加不明显,这是由于这一阶段红砂岩处于孔隙压密阶段,此时应变持续增加,但应力增加相对缓慢。第2阶段的红砂岩单元总应变能和可释放弹性应变能同步增加,耗散能几乎没有累积。此时红砂岩处于弹性变形阶段,几乎不产生塑性变形,总应变能全部作为弹性能储存在红砂岩中。第3阶段时红砂岩单元的耗散能开始累积,这表示红砂岩开始进入屈服阶段,初始裂纹扩展并伴随着新裂纹的形成,逐渐产生大量的塑性变形,该阶段的起点可以称为“起裂点”。
第4阶段时岩石单元中可释放弹性应变能开始降低,根据红砂岩是否完全破坏,可释放弹性应变能降低的原因不同。当红砂岩未完全破坏时,第4阶段称为卸载阶段。在这种情况下,红砂岩中的应力由于外部荷载的卸荷而下降,弹性应变能不能继续积聚,转而开始释放。由于红砂岩承受外部荷载后仍具有承载能力,释放的弹性应变能一部分转化为耗散能,另一部分转化为红砂岩变形恢复的能量传递到加载系统中。因此红砂岩单元的总应变能先增大后减小。当红砂岩完全破坏时,第4阶段称为破坏阶段。由于红砂岩产生了宏观破坏,承载能力降低。红砂岩中的应力开始下降,弹性应变能不能继续积聚,转而开始释放。释放的弹性应变能完全转化为耗散能,总应变能持续增加后趋于不变。因此,与红砂岩的变形阶段类似,能量演化曲线也可以划分为4个阶段:孔隙压密阶段、弹性变形阶段、岩石屈服阶段、岩石破坏(卸载)阶段。
为了精确划分不同能量演化阶段的起始时间,当岩石单元的总应变能、耗散能和可释放弹性应变能小于0.01 MJ/m3时视为没有明显增加。不同含水率下红砂岩各能量演化阶段起点所对应的时间见表 2。由表 2可以看出,不同含水率红砂岩弹性变形阶段的起始时间在17 μs到22 μs之间;起裂点的起始时间在47 μs到62 μs之间;破坏点的起始时间在84 μs到102 μs之间。这与高速摄像仪记录的岩石破坏过程相似,如图 10所示[23],通过高速摄像仪记录的岩石破坏过程与岩石应力应变曲线相对应,可知时间为96 μs时岩石表面萌生明显的裂纹,之后逐渐沿裂纹轴向扩展,在该过程中裂纹的扩展导致了应力的下降。另外,起裂点的起始时间约为64 μs,弹性变形阶段起始时间约为16 μs。
| 表 2 不同含水率下红砂岩各能量演化阶段起点所对应的时间 Table 2 Time corresponding to the starting point of each energy evolution stage of red sandstone with different water content |
 |
| 点击放大 |
 |
| 图 10 岩石承受冲击荷载时的应力应变曲线和高速摄影图像[23] Fig. 10 Stress-strain curves and high-speed photography images of rock under impact load[23] |
3.3 能量演化阶段的起始时间与含水率的关系
根据表 2中各能量演化阶段起点所对应的时间,可以得到红砂岩孔隙压密阶段、弹性变形阶段、屈服阶段的持续时间。红砂岩在3个能量演化阶段的持续时间随含水率的变化见图 11。由图 11可以看出,在同一含水率下,岩石屈服阶段历时最长,孔隙压密阶段历时最短。对比不同含水率下红砂岩孔隙压密阶段、弹性变形阶段、屈服阶段的历时可以看出,对于孔隙压密阶段,干燥砂岩在这一阶段历时最长。随着含水率的增加,孔隙压密阶段的历时总体呈下降趋势。这与Helong Gu等的试验结果吻合:相比于静态加载,动态加载下含水煤试件没有明显的孔隙压密阶段和排水现象[24]。这是由于水与岩石的黏结性比空气更好。在动态加载时,岩石骨架变形较快,孔隙中的水来不及被挤压排出,而空气很容易被挤压排出。水难以被压缩和排出导致岩石孔隙的实际可被压密体积减小。因此,低含水率红砂岩的孔隙压密阶段历时相对更长。
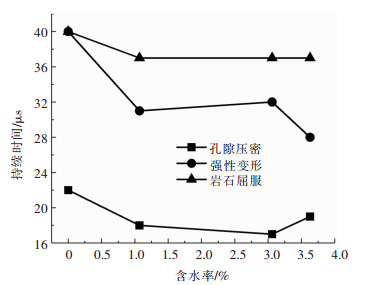 |
| 图 11 不同含水率下红砂岩各能量演化阶段的历时 Fig. 11 Duration of each energy evolution stage of red sandstone with different water content |
弹性变形阶段和岩石屈服阶段的历时也随含水率的增大而减少,这是由于随着含水率的提高,红砂岩的抗变形能力逐渐降低,更快达到屈服和破坏所需的应变。另外,3个阶段历时在较低含水率时大幅下降,而在接近饱和时下降相对更不明显,这与动态杨氏模量与含水率的变化关系类似,进一步说明了水对红砂岩的弱化效应随含水率的增加逐渐减弱。
根据表 2中红砂岩各能量演化阶段起始时间随含水率的变化,可以分析含水率对红砂岩变形历程的影响。红砂岩各能量演化阶段起始时间与含水率的关系见图 12。由图 12可以看出,红砂岩各能量演化阶段起点所对应的时间均随着含水率的增大先减小后趋于不变。结合红砂岩各能量演化阶段的历时和起始时间随含水率的变化,分析得出,当含水率较低时,随着含水率的提高,红砂岩初始裂纹闭合进入弹性阶段更早,相应的,红砂岩脱离弹性变形阶段达到起裂点也更早,达到起裂点后裂纹的扩展和萌生更快,出现宏观破坏的时间提前。然而,当红砂岩接近饱和时,含水率对红砂岩变形历程的影响可以忽略。红砂岩各能量演化阶段的起始时间随含水率的变化呈现出负指数关系,

|
(7) |
 |
| 图 12 各能量演化阶段的起始时间随含水率的变化 Fig. 12 Variation of the initial time of each energy evolution stage with water content |
式(7)中:tsi是不同含水率下某一能量演化阶段的起始时间,i可取e、y和f,分别表示弹性变形阶段、岩石屈服阶段和岩石破坏阶段;a+b是干燥砂岩在该能量演化阶段的起始时间,b是由水引起的该阶段的起始时间减少率。拟合公式中a,b的值见表 3。
| 表 3 各能量演化阶段的起始时间与含水率的拟合参数 Table 3 Parameters of fitting function of the relationship between the initial time of each energy evolution stage and water content |
 |
| 点击放大 |
3.4 能量-应变演化特性与含水率的关系
图 13展示了岩石单元的总应变能、可释放弹性应变能和耗散能随应变的变化。由图 13可以看出,红砂岩完全破坏时,其单位体积总应变能和耗散能随应变的增加而增加,并且增速先逐渐上升,然后趋于稳定。可释放弹性应变能随应变的增加先增大后减小。
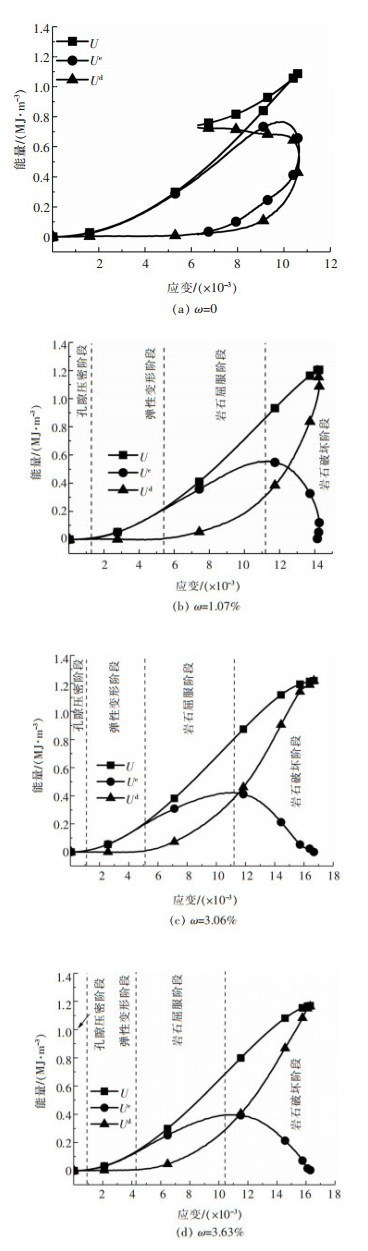 |
| 图 13 红砂岩在不同含水率下的能量-应变演化曲线 Fig. 13 Energy-strain evolution curve of red sandstone with different water content |
红砂岩未完全破坏时,在加载阶段,总应变能、可释放弹性应变能和耗散能均随应变的增加而增加。在卸载阶段,总应变能和可释放弹性应变能随应变的减小而减少,耗散能随应变的减小仍然增加。由于红砂岩未完全破坏时应变达到在卸载阶段减小,难以将各阶段在图中准确表示,图 13只将其它3种含水率的4个变形阶段表示了,但含水率为0的能量演化曲线同样可以准确地划分为4个能量演化阶段。
红砂岩各能量演化阶段起点所对应的应变与含水率的关系见图 14。
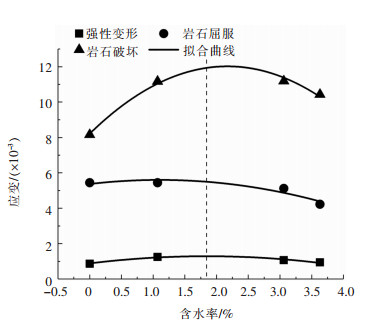 |
| 图 14 各能量演化阶段的起始应变随含水率的变化 Fig. 14 Variation of the initial strain of each energy evolution stage with water content |
由图 14可以看出,各阶段起始应变随含水率的增加均表现出先增后减的趋势,这表明红砂岩达到弹性变形阶段、岩石屈服阶段、岩石破坏(卸载)阶段时的变形随含水率的增大先增大后减小。3个阶段起点所对应的应变与含水率的关系均符合二次函数关系。
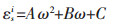
|
(8) |
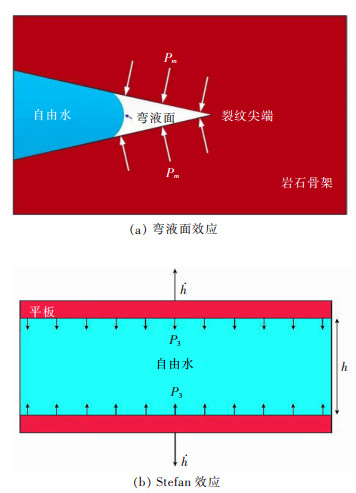
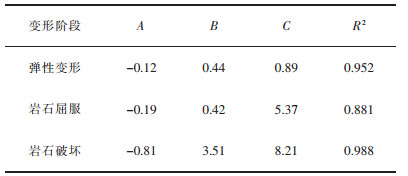
式(8)中:εsi是不同含水率下某一能量演化阶段的起始应变,i可取e、y和f,分别表示弹性变形阶段、岩石屈服阶段和岩石破坏阶段。拟合公式中的参数A、B和C见表 4。红砂岩各阶段起点应变随含水率的增加先增后减主要有2个原因,一方面水对红砂岩抗变形能力的削弱作用随含水率的增加逐渐减弱,这导致红砂岩在同一阶段内累积的变形不再随含水率的增大而增加;而另一方面,充满水的岩石孔隙会产生Stefan效应以及弯液面效应,如图 15所示[25]。动态加载过程中,由于裂纹扩展较快,水不能及时扩散到新产生的裂纹尖端,并形成弯液面产生拉力阻碍裂纹的扩展。同时,岩石裂纹面作为相距较近的2个平面,当其中填满水并有相互分开的趋势时,水会对裂纹施加一个相反的力阻碍其运动,即Stefan效应。这导致了当含水率达到一定限值时,红砂岩同一阶段内的累积变形反而随含水率的增加而减少。
| 表 4 各能量演化阶段的起始应变与含水率的拟合参数 Table 4 Parameters of fitting function of the relationship between the initial strain of each energy evolution stage and water content |
 |
| 点击放大 |
红砂岩达到破坏或卸载阶段的起点时,单位体积耗散能的占总应变能的比例可以直观地反映红砂岩在相同动荷载下累积塑性应变的能力。试件在破坏(卸载)点的单位体积能量耗散率可以表示为:
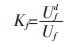
|
(9) |
式(9)中:Uf和Ufd是分别试件在破坏(卸载)点的单位体积总应变能和耗散能。破坏(卸载)点的能量耗散率随含水率的变化见图 16. 由图 16可以看出,Kf值随含水率的增加先上升后下降,这与破坏(卸载)阶段起点对应的应变随含水率的变化趋势相近,这表明红砂岩在相同动荷载下累积塑性应变的能力随含水率的增大先提高后减弱。由拟合曲线可知Kf与含水率之间也符合二次函数关系,即
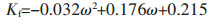
|
(10) |
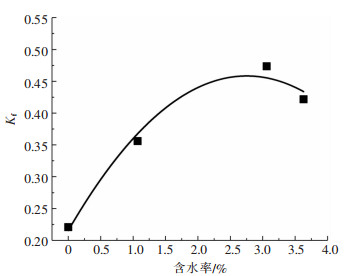 |
| 图 16 4种含水率下红砂岩在破坏(卸载)点处的能量耗散率 Fig. 16 The energy dissipation ratio of a red sandstone with four water content at the failure (unloading) point |
3.5 基于能量演化的损伤特性
岩石的变形损伤与耗散能密切相关,其损伤变量可以通过耗散能和岩石破坏时的最大耗散能的比值来定义:
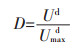
|
(11) |
式(11)中:Ud是单位体积耗散能;Umaxd是岩石破坏时的最大耗散能。由于干燥状态下红砂岩并未完全破坏,因此只研究另外3种含水率砂岩的损伤演化特性。图 17分别展示了3种含水率下红砂岩的损伤随时间、应变的演化关系。
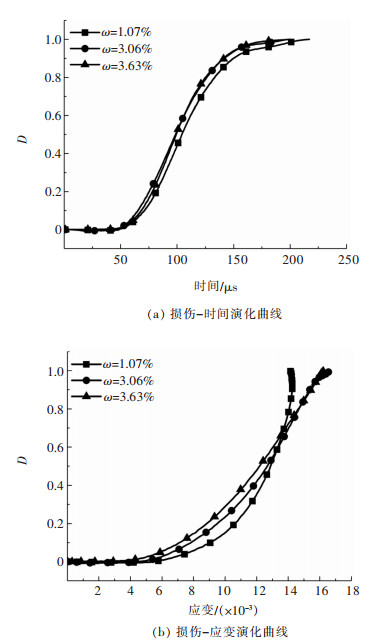 |
| 图 17 不同含水率下红砂岩的损伤-时间和损伤-应变演化曲线 Fig. 17 Damage-time and damage-strain evolution curves of red sandstone specimens with different water content |
由图 17(a)可以看出,冲击荷载下红砂岩的损伤随时间先平稳发展,然后逐渐增大,最后趋于平缓,变化趋势呈典型的的“S”型。当红砂岩处于孔隙压密阶段和弹性变形阶段时,随时间的增加,损伤几乎没有累积;到达起裂点后,红砂岩进入屈服阶段,产生塑性变形,损伤开始显著增加;在破坏阶段,损伤仍然增加但随时间的增速逐渐变缓,最后趋于不变。当含水率为3.06%和3.63%时,损伤随时间的演化趋势差别不大,而含水率为1.07%时损伤演化相对另外2种含水率更慢。
由图 17(b)可以看出,冲击荷载下红砂岩的损伤演化曲线随应变持续增大,单位应变下产生的损伤先增大而后趋于不变。当红砂岩处于孔隙压密阶段和弹性变形阶段时,随着应变的增加,损伤也几乎没有累积;达到屈服阶段后,损伤开始明显增加,单位应变下的损伤累积也增多;进入破坏阶段后,损伤依然随应变的增加而增加,但单位应变下的损伤累积几乎不变。相比于损伤随时间的演化,损伤随应变的演化趋势在不同含水率下的差别更加显著。单位应变下的损伤累积随含水率的增大而增加,虽然在应变较大时,含水率为1.07%的红砂岩单位应变下损伤累积反而超过了另外2种含水率,但这是由于含水率为1.07%的红砂岩最大动态应变相对较低导致的。
4 结论针对工程岩体处于不同水环境下的实际,对干燥状态、自然含水状态、自然饱水状态和强制饱水状态下的红砂岩开展了动态单轴压缩试验,研究含水率对红砂岩承受动载时的能量演化以及变形损伤特性的影响,主要结论如下:
1)红砂岩的动态峰值应力随含水率的增大而减小,最大动态应变随含水率的增大而增大,杨氏模量随含水率的增大先减小后趋于稳定,呈负指数关系。
2)根据能量演化规律可以看出,岩石屈服阶段和岩石破坏阶段的起点可以作为岩石的起裂点和宏观破坏发生点。随着含水率的增大,红砂岩在孔隙压密阶段的历时呈下降趋势,弹性变形阶段和岩石屈服阶段历时先缩短后趋于稳定。较低含水率下,红砂岩进入弹性阶段、裂纹开始扩展和萌生、出现宏观破坏的时间随均含水率的增大而提前,但在接近饱和时,3种行为出现的时间随含水率的提高变化不大。
3)红砂岩进入弹性阶段、裂纹开始扩展和萌生、出现宏观破坏时累积的变形随含水率先增大后减小。通过对红砂岩在破坏(卸载)点的单位体积能量耗散率的比较,红砂岩累积塑性应变的能力随含水率的增大也先增大后减小,与破坏(卸载)阶段起点对应的应变随含水率的变化趋势相近。
4)冲击荷载下红砂岩损伤随时间的演化曲线呈平稳发展—快速增加—趋于平缓的典型“S”型曲线,含水率为3.06%和3.63%时,损伤随时间的演化趋势几乎重合,而含水率为1.07%时损伤演化相对另外2种含水率更缓慢。红砂岩损伤随应变的增加持续增大并且增速先增加后趋于不变。
| [1] |
MA D, CAI X, LI Q, et al. In-Situ and Numerical investigation of groundwater inrush hazard from grouted karst collapse pillar in Longwall mining[J].
Water, 2018, 10(9): 1187–1204. DOI: 10.3390/w10091187. |
| [2] |
MA D, DUAN H Y, CAI X, et al. A global optimization-based method for the prediction of water inrush hazard from mining floor[J].
Water, 2018, 10(11): 1618–1635. DOI: 10.3390/w10111618. |
| [3] |
MA D, CAI X, ZHOU Z L, et al. Experimental investigation on hydraulic properties of granular sandstone and mudstone mixtures[J].
Geofluids, 2018. |
| [4] |
夏开文, 徐颖, 陈荣. 考虑深部赋存条件的岩石动态破坏试验研究进展[J].
隧道与地下工程灾害防治, 2019, 1(1): 58–75.
|
| [5] |
邓飞, 韩晓亮, 罗福友, 等. 不同含水状态砂岩损伤分析研究[J].
有色金属科学与工程, 2014, 5(6): 95–99.
|
| [6] |
王斌, 李夕兵, 尹土兵, 等. 饱水砂岩动态强度的SHPB试验研究[J].
岩石力学与工程学报, 2010, 29(5): 1003–1009.
|
| [7] |
KIM E, CHANGANI H. Effect of water saturation and loading rate on the mechanical properties of red and buff sandstones[J].
International Journal of Rock Mechanics and Mining Sciences, 2016, 88: 23–28. DOI: 10.1016/j.ijrmms.2016.07.005. |
| [8] |
王浩宇, 许金余, 王鹏, 等. 含水岩石动态抗压强度与微观机制[J].
空军工程大学学报(自然科学版), 2016, 17(4): 107–111.
|
| [9] |
李天斌, 陈子全, 陈国庆, 等. 不同含水率作用下砂岩的能量机制研究[J].
岩土力学, 2015, 36(增刊2): 229–236.
|
| [10] |
LU A H, HU S C, LI M, et al. Impact of moisture content on the dynamic failure energy dissipation characteristics of sandstone[J].
Shock and Vibration, 2019. |
| [11] |
WANG P, XU J Y, FANG XY, et al. Energy dissipation and damage evolution analyses for the dynamic compression failure process of red-sandstone after freeze-thaw cycles[J].
Engineering Geology, 2017, 221: 104–113. DOI: 10.1016/j.enggeo.2017.02.025. |
| [12] |
WONG LNY, MARUVANCHERY V, LIU G. Water effects on rock strength and stiffness degradation[J].
Acta Geotechnica, 2015, 11(4): 713–737. |
| [13] |
袁璞, 马瑞秋. 不同含水状态下煤矿砂岩SHPB试验与分析[J].
岩石力学与工程学报, 2015, 34(增刊1): 2888–2893.
|
| [14] |
ZHOU Y X, XIA K, LI X B, et al. Suggested methods for determining the dynamic strength parameters and mode-Ⅰ fracture toughness of rock materials[J].
International Journal of Rock Mechanics and Mining Sciences, 2012, 49: 105–112. DOI: 10.1016/j.ijrmms.2011.10.004. |
| [15] |
SOLECKI R, CONANT RJ.
Advanced mechanics of materials[M]. London: Oxford University Press, 2003.
|
| [16] |
黄达, 黄润秋, 张永兴. 粗晶大理岩单轴压缩力学特性的静态加载速率效应及能量机制试验研究[J].
岩石力学与工程学报, 2012, 31(2): 245–255.
DOI: 10.3969/j.issn.1000-6915.2012.02.003.
|
| [17] |
李天斌, 陈子全, 陈国庆, 等. 不同含水率作用下砂岩的能量机制研究[J].
岩土力学, 2015, 36(增刊2): 229–236.
|
| [18] |
WAWERSIK W R, FAIRHURST C. A study of brittle rock fracture in laboratory compression experiments[J].
International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts, 1970, 7(5): 561–575. |
| [19] |
GONG F Q, SI X F, LI X B, et al. Dynamic triaxial compression tests on sandstone at high strain rates and low confining pressures with split hopkinson pressure bar[J].
International Journal of Rock Mechanics and Mining Sciences, 2019, 113: 211–219. DOI: 10.1016/j.ijrmms.2018.12.005. |
| [20] |
郭宏云, 赵健, 柳培玉. 深部软岩与水作用后的强度软化特性及化学分析[J].
岩石力学与工程学报, 2018, 37(增刊1): 3374–3381.
|
| [21] |
贾海梁, 王婷, 项伟, 等. 含水率对泥质粉砂岩物理力学性质影响的规律与机制[J].
岩石力学与工程学报, 2018, 37(7): 1618–1628.
|
| [22] |
LAIRD D A. Influence of layer charge on swelling of smectites[J].
Applied Clay Science, 2006, 34(1): 74–87. |
| [23] |
ZHANG Q B, ZHAO J. A review of dynamic experimental techniques and mechanical behaviour of rock materials[J].
Rock Mechanics and Rock Engineering, 2013, 47(4): 1411–1478. |
| [24] |
GU H L, TAO M, LI X B, et al. Dynamic response and failure mechanism of fractured coal under different soaking times[J].
Theoretical and Applied Fracture Mechanics, 2018, 98: 112–122. |
| [25] |
ZHOU Z L, CAI X, ZHAO Y, et al. Strength characteristics of dry and saturated rock at different strain rates[J].
Transactions of Nonferrous Metals Society of China, 2016, 26(7): 1919–1925. |
 2021, Vol. 12
2021, Vol. 12