| 岩石应力波分形分析方法的研究 |
岩石(体)应力波传播衰减规律是采矿工程和地下岩体工程等领域的关键问题,通过应力波传播衰减规律可反演岩石(体)物理力学性能,例如岩体动态参数测试、岩体结构分类、岩体松动层厚度确定、围岩支撑压力及地应力测试等。对应力波传播试验结果的充分利用是应力波反演的前提,通过对应力波分析技术的研究,有助于应力波数据高效利用以反演岩石(体)特性。
关于应力波传播衰减特性的研究,大多都从理论推导和应力波传播试验着手,以不同的表征参数分析应力波在岩石(体)中的传播规律。FAN等使用应力波波速对地应力下应力波传播展开了研究,得出了当地应力足够大时波速将接近完整岩体中的波速的结论[1]。HAN等利用透反射系数研究了填充节理厚度对应力波传播的影响,发现了随着填充厚度的增加,应力波的透射系数和能量均减小[2]。LI等从应力波能量的角度分析节理的粗糙度对应力波传播的影响规律,指出了应力波能量耗散会随着节理粗糙度的增大而增大[3]。李新平等采用应力波幅值分析了应力波在完整岩体中的几何衰减,明确了随着围压的增加, 透射系数呈现出先增大后减小的变化趋势[4]。刘少虹等采用应力波能量研究了动静组合下煤岩的应力波传播规律,发现了能量耗散随着静载的增大呈现先增大后减小的趋势[5]。金解放等分析了应力波透反射系数和围压的关系,指出了在长试件下透射系数和反射系数均与围压呈二次函数关系[6]。然而,上述分析方法都只从岩石应力波波形单方面进行了研究,对包含信息更丰富的整体波形却很少探索。
岩石应力波波形则是包含了应力波传播衰减的全部信息的具体体现,借助分形理论可以为研究岩石应力波波形揭示更多信息。FENG等采用盒维数对岩爆过程中的微震能量进行分析,得出微震事件能量分形维数越大岩爆强度越大的结论[7]。钱波等运用盒维数对围岩宏观变形进行研究,发现了分形维数可以为围岩变形起到预警作用[8]。赵奎等利用分形理论对声发射波形进行研究,提出了声发射波形关联维数值可以反映岩石的破坏程度[9]。苏国韶等针对岩爆中声音波形采用盒维数分析,指出声音的分形维数特征可以作为岩爆发生的前兆[10]。李楠等应用分形理论研究了煤矿微震不同阶段的分形特征,论证了冲击破坏前微震波形分形特征量作为冲击地压微震监测预警的可能性[11]。MONDAL等运用分形维数监测矿井地层压力可以为矿井坍落提供预警[12]。因此,借助分形维数可以为研究岩石应力波波形提供新的途径。
本文基于无轴向静应力下砂岩应力波传播试验数据,对岩石应力波分形分析方法进行研究。根据应力波时间序列的特点,分别采用了盒维数和关联维数对其进行分形计算,并对分形维数在岩石应力波上的计算和意义进行研究。试验结果有利于对应力波数据的有效利用处理以及分形探讨。
1 应力波传播试验及结果 1.1 试件岩石试件采用均质性良好的赣州红砂岩,其中试件单轴抗压强度为52 MPa,试件尺寸为80 mm×80 mm×1 500 mm。应变片黏贴位置如图 1所示:5个应变片依次相隔20 cm均匀对称粘贴在试件中轴线上,以减小试件出现偏心压缩对试验数据造成干扰。根据圣维南原理,为了得到均匀应力波,第1个应变片与入射端的距离应远大于横截面尺寸,因此本文定为15 cm;为了最后一个应变片能够测得一个完整的应力波信号(即不受反射波信号的叠加),最后一个应变片与试件透射端应有足够的距离,根据试验验证可知,当应变片距离透射端55 cm能满足上述要求。
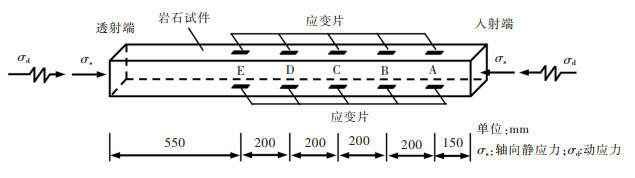 |
| 图 1 试件尺寸及应变片位置示意 Fig. 1 Schematic diagram of specimen size and strain gauge position |
为研究岩石应力波波形分形特性,宜采用无轴向静应力的工况以减少其他变量影响。因此,基于SHPB试验系统,使用图 1中的岩石长试件代替缓冲杆,进行无轴压下的应力波传播试验,试验装置详情见参考文献[13]。
1.2 试验结果通过应力波传播试验,可以得到无轴向静应力下的5组岩石应力波数据,如图 2所示。从图 2中可以看出,在不同的传播距离下,应力波的形状不发生明显变化,均为半正弦波形。而每个应力波均没有明显周期性、多层次性以及自相似特性,且不具备整体形状和局部特征形状相似的特点。
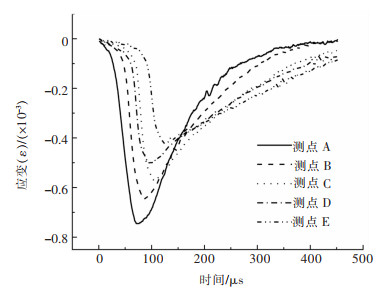 |
| 图 2 岩石应力波试验数据 Fig. 2 Experiment data of rock stress wave |
在使用分形维数分析岩石应力波分形特性时,应力波时间序列长度会对分形维数值产生影响。为减小序列长度对试验结果的影响,应力波波长做统一处理,采用应力波最小持续时间452 μs,后文有关应力波试验分析均采用等长的5组试验数据。
2 岩石应力波盒维数分形维数在刻画对象的分形特征时,常常需要根据对象结构的自相似程度以及特点选取相应的维数进行计算,其中分形盒维数定义简单,计算方便,在计算一般统计自相似对象中具有较好的优势,被广泛应用于规则分形中。而岩石应力波波形为半正弦波性,忽略波形震荡具有的对称性,符合一般统计自相似特点。因此,采用盒维数对岩石应力波波形进行分形特性研究。
2.1 岩石应力波盒维数的定义分形盒维数是应用覆盖法,以不同尺度的个体填充对象整体,从而计算对象结构精细程度随尺度变化的计算方法。设岩石应力波时间序列X是n维欧几里得空间R的任意非空有界子集,对于任意一个尺度r > 0,都可以将空间R划分成边长为r的正方形网格,若Nr表示用来表示覆盖集合X所需边长为r的n维体的最小数目,则盒维数可以定义为下式[14]。

|
(1) |
在计算过程中,需要使用不同尺度r的n维体去覆盖集合时间序列X,并计算所需要的最少数量Nr。然后在双对数坐标上,描绘出系列点{lnr, lnNr},并在线性较好的区间内,用最小二乘线性回归法求出不同尺度r下的系列点的斜率,即所求的盒维数。
考虑到实际计算中,由于数据精度和计算软件的有限性,往往不能使尺度r无限趋于零,从而得到相应的盒维数。针对这类问题,本文盒维数中采用的最小尺度r为应力波最小非零幅值差,最大尺度为试验波长进行计算。考虑到计算数据的有限性,且不同数据点拟合斜率偏差小于10%,故无标度区间采用全部尺度r。各测点下的应力波的双对数坐标均相似,这里仅给出A测点的双对数坐标,如图 3所示。
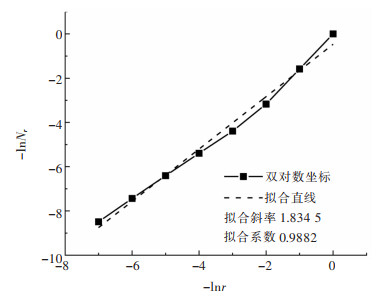 |
| 图 3 双对数坐标(A测点) Fig. 3 Logarithmic coordinates (measurement point A) |
2.2 岩石应力波盒维数的意义
按照上文应力波盒维数的定义,可以计算出不同传播距离下的应力波盒维数,如表 1所列,其中各拟合系数均大于0.97。从表 1可以看出,不同测点下的应力波均可以通过定义计算出相应的盒维数,且应力波盒维数均不同,但都集中在1.17左右。同时表 1中还给出了直线和Logistic吸引子时间序列的盒维数,可以发现,直线盒维数接近1,吸引子的盒维数为最大,应力波盒维数大于直线且小于吸引子,并且所有时间序列的盒维数均介于1和2之间。
| 表 1 不同时间序列的盒维数 Table 1 Box dimensions of different time series |
 |
| 点击放大 |
由拓扑维数的理论有:直线的拓扑维数为1,平面的拓扑维数为2,而不同密度直线组成的平面具有介于1和2之间的分数维数[15]。试验中直线计算的盒维数为1.082,误差为8%,主要原因是试验数据长度与计算软件二进制性质不匹配导致的,并且误差大小在接受的范围内。而岩石应力波作为介于一维直线和二维平面的离散数据点,不同于直线,又不属于平面,归属于不同直线的离散点组成平面点集,应具有介于1和2的分形维数,与试验结果吻合。吸引子具有明显的多层次结构以及复杂的时间序列,应具有比应力波更大的分形维数[16],与计算所得相符。
盒维数作为分形理论中刻画对象整体与局部的相似性参数,主要与应力波曲线的波动程度有关,曲线波动越大,盒维数越大[17]。由表 1可以看出,岩石应力波波形的盒维数大于直线小于吸引子,而岩石应力波波形复杂程度大于直线又小于吸引子,因此,岩石应力波盒维数可以反映出曲线的复杂程度。另外随着传播距离的增加,岩石应力波波形的盒维数也有不同,这表明岩石应力波的盒维数可以反映岩石应力波波形的差异。
3 岩石应力波关联维数关联维数作为分形理论中的重要概念,主要利用关联积分来计算变量前后的关联性,以此来描述序列的确定性规律及其程度,从而定量说明事物的复杂度和不规整度。Grassberger和Procaccia提出的G-P算法是目前定义和计算关联维数的经典方法,主要部分包括重构相空间和定义关联维数,可以分别从自相似性和标度不变性对岩石应力波波形进行分形研究。因此,分别从重构相空间和关联维数对岩石应力波分形分析方法进行研究。
3.1 重构相空间重构相空间的基本思想是,系统任一分量的演化都由其自身与其它分量作用后共同决定的,并且其演化信息隐藏在全体分量中。因此,可以通过对序列进行重构相空间,并计算相空间中点集的相关程度,从而为研究序列分形特性提供理论依据。
将岩石应力波时间序列作为随时间变化的序列X={x1,x2,x3,…,xn},采用时间差法重构相空间[18]。即从序列中的第1个量起按一定的延迟时间τ,从序列中取序列值作为矢量的分量Xi=[xi, xi+τ, xi+2τ, …, xi+(m-1)τ],以此来构造一批相空间维数为m,矢量个数为N=n-(m-1)τ的矢量X=[X1, X2, X3, …, XN]T,用作扩展到高维空间恢复系统原有的特性,如式(2)。
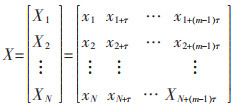
|
(2) |
考虑到不同测点下的岩石应力波波形相似,且波长一致,相空间展开形状均相似,这里仅将A测点下应力波进行重构相空间演示,并绘制不同相空间的应力波矢量分量如图 4所示。从图 4中可以看出,不同相空间维数下,应力波相空间呈现出不同的形状。当维数较小时,应力波相空间为杂乱无章且线条交错的形状;当维数等于6时,应力波相空间仍然为混乱形状,但开始呈现出收敛的趋势了;当维数等于10和12时,应力波相空间为明显地先减小后增大的形状了,并且最终均趋于一定的值。不同测点下的应力波重构相空间均相似,都是随着相空间维数的增大,均将最终趋于一定的值内。
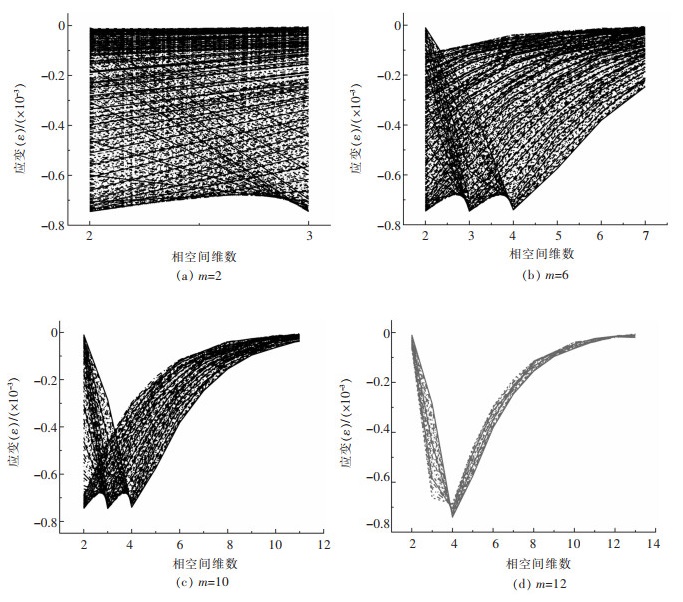 |
| 图 4 不同相空间下A测点下应力波相空间 Fig. 4 Phase space diagram of stress waves at measuring point A |
相空间代表着系统可能具有原有状态的集合,在计算关联维数时应尽可能包含多的可能性。将应力波时间序列进行重构相空间,其中的延迟采用自相关函数计算取得,由N=n-(mmax-1)τ > 0可得mmax < (n/τ)+1,可以确定相空间维数最大取值范围为2至12,后文关联维数的定义和计算均在此相空间内。
3.2 岩石应力波关联维数的定义及参数取值在m维重构相空间中随意选取一点Xi做参考点,计算剩余N-1个点集到参考点的距离。统计剩余点中距离小于小标量r的个数,可以得到相应的关联积分,即式(3),从而可以得到该尺度r下的系列点{lnCm(r), lnr}。若这些点排列为直线,则说明岩石应力波信号在给定的尺度r范围内具有分形特征。对这些点使用最小二乘法进行拟合,所得直线斜率就是岩石应力波波形的关联维数[19]。

|
(3) |
式(3)中:H为Heaviside跃迁函数;‖X(i)-X(j)‖为两相点之间的距离,本节采用一范数进行计算[20];标量r根据应力波数据实际尺度取得。
在使用G-P算法计算应力波的关联维数时,参数的选取具有较大的主观性,而不同的参数选取都将影响结果的正确性[21]。为了能够得到一个可靠的关联维数值,需要对其中的参数的选取进行确认。但由于应力波数据复杂,计算参数较多,并且相互影响,取值确认繁琐。限于篇幅,本文并未给出论证过程,仅给出参数计算时使用的方法及其取值。
研究表明序列长度对关联维数有较大的影响,主要体现在数据序列长度的取值与关联维数呈指数关系,并可以影响关联维数的精度[21]。而应力波序列长度不同,即单个应力波持续时间波会因传播距离的不同而有所变化,但由于这种波长的变化是因为传播距离产生的,属于岩石应力波波形范畴内。为避免数据长度对关联维数的影响,将采用等长的应力波时间序列进行计算分析,应力波传播试验采样时间为1 ms,序列长度取岩石应力波最小持续时间n=452 μs。
关联维数是标量r的函数,也是岩石应力波波形序列具有分形现象的尺度,一般标量的取值根据实际试验数据尺度得到。由式(3)可以看出,标量的取值包括标量的大小范围和序列关系,而后者根据情况可以分为取值序列的长度和序列间的数据关系。根据文献[22]表明,标量的上限为使关联维数的对数lnC(r)接近为0的取值,下限为使关联维数接近相空间维数时的取值,具体范围需经过多次试验取值后,迭代计算最终确定取值范围。本节计算过程中标量采用的取值范围介于e-1~e0之间,序列的长度为21,按等距离间隔0.05取值。
延迟时间和相空间维数均是重构相空间中的关键参数[23],旨在将序列中隐藏信息通过恢复到原始状态展现出来。现有理论在处理相空间重构方面有着截然不同的观点,一种是认为延迟时间和相空间维数互不相关,可以分别计算得到;另外一种认为2个参数相互依赖,可同时计算出2个的取值。本节依据重构相空间理论,分别独立计算2个参数。其中延迟时间由岩石应力波采用自相关函数法求的[24],对于应力波的自相关函数如式(4)。
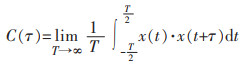
|
(4) |
式(4)中:当C(τ)的值下降到1-(1/e)所用的间隔就是延迟时间。考虑到不同测点下岩石应力波波形的差异性较大,在计算关联维数时,采用由各自计算所得的延迟时间,不做统一处理。随着传播距离的增大,各测点下应力波的延迟时间分别取39, 36, 33, 32, 34。
无标度区间取值会对关联维数产生影响[25],在计算不同测点下的关联维数时,应根据数据特点取得。本节采用饱和试算法取得,以A测点下的应力波为例说明,标量首先取值-5至0,按等距离间隔0.1取值,序列的长度为51,延迟时间取39,相空间维数取最大范围2至12,计算参数取值确定过程如图 5所示。从图 5(a)中可以看出,当相空间维数较小时,系列点{lnCm(r), lnr}在标量较小区间排列为平稳增大,在标量区间较大的区间为快速增大;当相空间维数较大时,系列点呈现为横直线,并且在标量区间e-1~e0内,系列点排列呈斜直线。故可以将标量区间重新取值,重新往复计算,直至标量区间内的系列点呈现为斜直线。
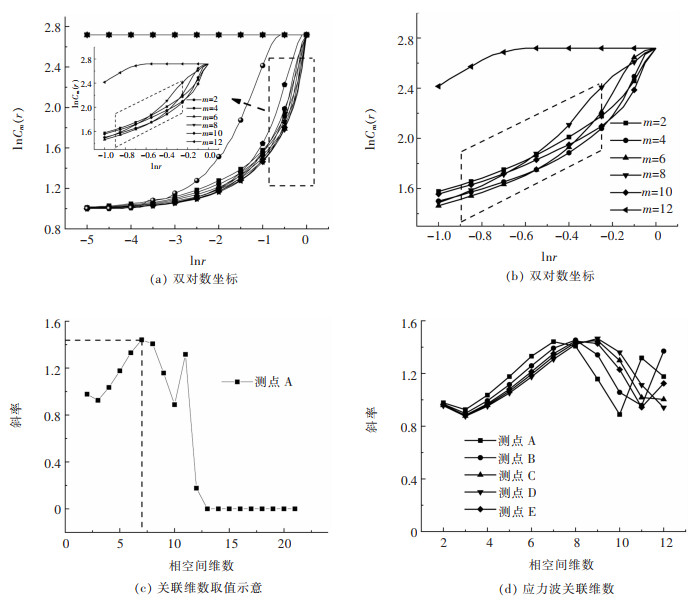 |
| 图 5 关联维数计算示意 Fig. 5 Calculation schematic diagram of correlation dimension |
当标量区间取值合适时,系列点排列呈现为斜直线,如图 5(b)所示。从图 5中可以看出,在限定的标量区间内,不同相空间维数所计算出来的系列点排列近似为斜直线,并且系列点呈现的倾斜程度与相空间维数有关。在限定的标量区间内,取系列点集中线性区间较好的部分可以求得关联维数。该线性区间就是分形无标度区间,也是序列分形存在的尺度范围,这里采用斜率偏差正负10%以内作为无标度区间。
3.3 岩石应力波关联维数的意义在系列点中选取线性程度较好的区间,采用最小二乘法求得关联维数与相空间维数的关系,如图 5(c)所示。由图 5可以看出,随着相空间的增大,系列点排列斜率先增加;当相空间维度m=7时,斜率达到最大值,而后趋于在一定范围内震荡,直至迅速下降至0。故本次研究的相空间维数取值为7,斜率最大值就是本文应求的关联维数值。按照上述计算方法以及参数设置,将应力波关联维数示意图描述如图 5(d)所示。从图 5可以看出,不同测点下的岩石应力波波形计算出来的系列点斜率与相空间具有相同的变化趋势,均是随着相空间维数的增大,出现先增大后减小的变化趋势,各曲线的峰值介于1.42和1.48之间,拐点位于7和9之间。
不同测点下的岩石应力波波形均能通过G-P算法计算出相应的关联维数,并且拟合系数均大于0.96,这表明不同测点下的应力波在相应的标量区间内具有相似的结构。考虑到计算过程中标量区间的取值为e-1~e0,上述应力波相似结构均建立在应力波最小尺度范围内,在更大的尺度内并没有体现出相似特性。因此,应力波的关联维数值不能反映岩石应力波波形上的相似性。
4 结论基于岩石应力波传播试验数据,研究了岩石应力波波形的盒维数和关联维数的计算方法和意义,可以得到以下主要结论。
1)基于分形盒维数理论,可以计算出岩石应力波的盒维数,其中不同测点下的岩石应力波的盒维数为1.14~1.18。分形盒维数能够反映波形的复杂程度,维数越大,波形复杂程度越大。
2)依据G-P算法,可以计算出岩石应力波关联维数,其中不同测点下岩石应力波波形的关联维数为1.42~1.48。应力波关联维数仅够反映应力波波形在最小尺度的相似性,不能反映出波形上的相似。关联维数计算中相空间维数为7~9;相空间维数取值范围为2至12;标量取值范围介于e-1~e0之间,序列的长度为21,按等距离间隔0.05取值;延迟时间采用自相关法求得。
3)应力波波形是初始波形与岩石作用后共同形成的,在使用应力波波形的分形维数辨析岩石破碎情况时前,需剔除前者的因素。
| [1] |
FAN L F, SUN H Y. Seismic wave propagation through an in-situ stressed rock mass[J].
Journal of Applied Geophysics, 2015, 121: 13–20. DOI: 10.1016/j.jappgeo.2015.07.002. |
| [2] |
HAN Z Y, LI D Y, TAO Z., et al. Experimental study of stress wave propagation and energy characteristics across rock specimens containing cemented mortar joint with various thicknesses[J].
International Journal of Rock Mechanics and Mining Sciences, 2020, 131: 104352. DOI: 10.1016/j.ijrmms.2020.104352. |
| [3] |
LI J C, RONG L F, LI H B, et al. An SHPB test study on stress wave energy attenuation in jointed rock masses[J].
Rock Mechanics and Rock Engineering, 2019, 52: 403–420. DOI: 10.1007/s00603-018-1586-y. |
| [4] |
李新平, 董千, 刘婷婷, 等. 地应力下柱面应力波在节理岩体中传播规律研究[J].
岩石力学与工程学报, 2018, 37(增刊1): 3121–3131.
|
| [5] |
刘少虹, 毛德兵, 齐庆新, 等. 动静加载下组合煤岩的应力波传播机制与能量耗散[J].
煤炭学报, 2014, 39(增刊1): 15–22.
|
| [6] |
金解放, 王杰, 郭钟群, 等. 围压对红砂岩应力波传播特性的影响[J].
煤炭学报, 2019, 44(2): 435–444.
|
| [7] |
FENG X T, YU Y, FENG G L., et al. Fractal behaviour of the microseismic energy associated with immediate rockbursts in deep, hard rock tunnels[J].
Tunnelling and Underground Space Technology, 2016, 51: 98–107. DOI: 10.1016/j.tust.2015.10.002. |
| [8] |
钱波, 徐奴文, 肖培伟, 等. 双江口水电站地下厂房顶拱开挖围岩损伤分析及变形预警研究[J].
岩石力学与工程学报, 2019, 38(12): 2512–2524.
|
| [9] |
赵奎, 王更峰, 王晓军, 等. 岩石声发射Kaiser点信号频带能量分布和分形特征研究[J].
岩土力学, 2008(11): 3082–3088.
DOI: 10.3969/j.issn.1000-7598.2008.11.034.
|
| [10] |
苏国韶, 石焱炯, 冯夏庭, 等. 岩爆过程的声音信号特征研究[J].
岩石力学与工程学报, 2016, 35(6): 1190–1201.
|
| [11] |
李楠, 李保林, 陈栋, 等. 冲击破坏过程微震波形多重分形及其时变响应特征[J].
中国矿业大学学报, 2017, 46(5): 1007–1013.
|
| [12] |
MONDA L D, ROY PNS, BEHERA P K. Use of correlation fractal dimension signatures for understanding the overlying strata dynamics in longwall coal mines[J].
International Journal of Rock Mechanics and Mining Sciences, 2017, 91: 210–221. DOI: 10.1016/j.ijrmms.2016.11.019. |
| [13] |
金解放, 程昀, 昌晓旭. 轴向静载对红砂岩中应力波传播特性的影响试验研究[J].
岩石力学与工程学报, 2017, 36(8): 1939–1950.
|
| [14] |
周翠英, 梁宁, 刘镇. 红层软岩压缩破坏的分形特征与级联失效过程[J].
岩土力学, 2019, 40(增刊1): 21–31.
|
| [15] |
朱华, 姬翠翠.
分形理论及其应用[M]. 北京: 科学出版社, 2011.
|
| [16] |
喻敏, 王斌, 王文波, 等. Logistic混沌系统分形特性研究[J].
数学的实践与认识, 2014, 44(23): 273–277.
|
| [17] |
龙源, 晏俊伟, 娄建武, 等. 基于分形理论的爆破地震信号盒维数研究[J].
科技导报, 2007(18): 27–31.
DOI: 10.3321/j.issn:1000-7857.2007.18.006.
|
| [18] |
吕金虎, 陆君安, 陈士华.
混沌时间序列分析及其应用[M]. 武汉: 武汉大学出版社, 2005: 60-61.
|
| [19] |
曾鹏, 纪洪广, 高宇, 等. 三轴压缩下花岗岩声发射Kaiser点信号频段及分形特征[J].
煤炭学报, 2016, 41(增刊2): 376–384.
|
| [20] |
党建武, 黄建国. 基于G.P算法的关联维计算中参数取值的研究[J].
计算机应用研究, 2004(1): 48–51.
DOI: 10.3969/j.issn.1001-3695.2004.01.014.
|
| [21] |
戴维凯, 张胜, 吴峰, 等. 嵌入空间的复杂网络关联维数研究[J].
南昌航空大学学报(自然科学版), 2020, 34(3): 25–33.
|
| [22] |
付强, 李晨溪, 张朝曦. 关于G-P算法计算混沌关联维的讨论[J].
解放军理工大学学报(自然科学版), 2014, 15(3): 275–282.
|
| [23] |
施泽进, 李忠权, 应丹琳. 序列数据关联维的计算及意义[J].
成都理工学院学报, 1996(2): 88–92.
|
| [24] |
于青. 关联维数计算的分析研究[J].
天津理工学院学报, 2004, 20(4): 60–62.
DOI: 10.3969/j.issn.1673-095X.2004.04.018.
|
| [25] |
周双. 混沌时间序列中最大Lyapunov指数与关联维数的无标度区间自动识别研究[D]. 北京: 中国科学院重庆绿色智能技术研究院, 2016.
|
 2021, Vol. 12
2021, Vol. 12


