| 非均一极距对稀土电解多相流影响的数值模拟及实验验证 |
2. 赣州嘉通新材料有限公司, 江西 赣州 341000;
3. 江西离子型稀土工程技术研究有限公司, 江西 赣州 341000
2. Ganzhou Jiatong New Materials Co., Ltd., Ganzhou 341000, Jiangxi, China;
3. Jiangxi Ionic Rare Earth Engineering Research Co., Ltd., Ganzhou 341000, Jiangxi, China
稀土电解槽内的流体运动属于电场、热场、阳极气泡等多因素作用下的多相流运动,且不同的因素之间不仅相互作用,还各自对电解槽的正常运行有着不同程度的影响。稀土电解槽内流体运动的最主要原因是电解过程中在阳极炭块上进行电化学反应逐渐消耗并持续产生阳极气泡,阳极气泡从阳极的内表面反应生成和逸出过程对阴阳两极间的电解质起到强烈的搅拌作用。同时,槽内浓度梯度和温度梯度受极距的影响,使各相流体在槽内运动的过程中会产生强烈的湍动,体现为涡运动特征,其也与电极电流密度、稀土氧化物的溶解速度等指标有关。因此,研究电解槽内电解过程中各个物理场以及电化学参数的变化显得十分重要。Solheim等通过求解连续方程模拟计算,并且探索了阳极表面气体运动过程对槽内电解质的影响情况[1],刘庆生等通过fluent模拟研究了稀土电解槽内不同时间、电流密度、极距的阳极气泡对流场的影响及气含率分布[2],Bilek等利用Fluent对电磁力和阳极气体对电解槽内流体的影响进行了相关的仿真工作[3]。
对于稀土电解槽,极距是决定稀土电解槽运行过程中槽况稳定的核心参数之一。由于电解质的电阻率很大,极间电解质会产生较大功耗,如果过分地增大或降低极距则会引起电解过程的波动,也会对电流效率产生不同幅度的影响,所以对极距的优化是研究的关键。因阳极消耗速度与电流有关,导致阳极消耗的“自平衡性”,即极间距较大一侧的阳极经过的电流较小,消耗较慢;反之极间距较大一侧具有较大的电流,消耗速度快。且随着电解进行,所有的极距的差异性会逐渐减小直到极距相同。但实际上,因换极、阳极效应等原因,导致阳极电流并不能均匀分布。姜艳丽等通过仿真模拟计算了恒压状态下电解槽内电场的分布[4],刘中兴等进行了在电极插入不同深度下对稀土电解槽电热场的影响做了相关模拟研究[5],丁培林等建立铝电解槽电解质浓度-热场瞬态模型,研究了铝电解槽下料过程对电解质温度场的影响[6]。上述研究虽然从各个因素对电解过程的影响程度做了一定的工作,但却假定电解槽极距分布是均一且对称的,而忽略了实际生产中阳极炭块在电解过程中往往不是均匀消耗,且极距分布是不均一的。到目前为止,尚未发现有学者对非均一极距下稀土电解槽内的各物理场和电化学参数等指标进行研究。
本文对3 500 A稀土电解槽进行研究,在作者提出的稀土金属液-电解质-阳极气泡模型和非均一分布模型的基础上,开展了非均一极距下的电场、温度场、阳极气泡、电解质流场和稀土金属液滴的数学建模和仿真工作,并利用等距压降法[7]测阳极电流,与Fluent计算的电流值进行对比,对模型的可靠性进行了验证。模拟的主要内容包括非均一极距下稀土电解槽内的电场、热场的分布规律以及非均一极距下的阳极气泡、电解质流场和稀土金属液滴的运动状态,分析了不同非均一性极距下槽内各物理场以及电化学参数的变化规律,对优化电解槽的整体操作,提高电解效率以及降低能耗等方面提供了一定程度的指导作用[8]。
1 数学模型 1.1 数学物理方程 1.1.1 电场控制方程对于稀土熔盐电解的过程,可以将电场的基本方程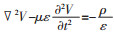
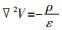
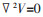
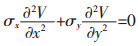
|
(1) |

|
(2) |
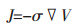
|
(3) |
式中:V为标量电位,V;ρ为自由电荷密度,c/m3;I为电流,A;R为电阻,Ω;σ为电导率,Ω-1·m-1;J为电流密度,A/m2。
1.1.2 温度场控制方程根据热传导的定律,得出电解的温度场基本方程,温度场控制方程为[12-13]:
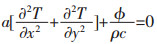
|
(4) |
式中:a为热扩散系数,m2/s;ϕ为单位时间内的生成热,W/m3;ρ为密度,kg/m3;c为比热容,J/(kg·K)。
1.1.3 流场控制方程基于欧拉—欧拉法建立的多相流非均相稳态模型,对于电解槽内的气体、电解质流体和液相稀土金属,控制方程表示如下[14]:
质量守恒方程:

|
(5) |
动量守恒方程:

|
(6) |
气泡体积浮力为:

|
(7) |
式中:ρg与ρb为气体和电解质密度,边界条件为:
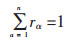
|
(8) |
这里Uα、rα与ρα为流速、体积分数和密度;μαeff为α相的有效黏度,即分子黏度μα和湍流黏度μT之和;Mα表示其它对α的作用力;SMα为α的体积力;n为流体相的数量[15-16]。
1.1.4 湍动能及耗散率方程
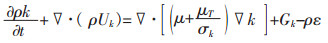
|
(9) |

|
(10) |
k与ε为动能和耗散[17],cμ=0.09,C1=1.44,C2=1.92,σk=1.0,σε=1.3。
1.2 非均一性模型新换阳极的影响,使得各阳极炭块与阴极的距离不同,这是造成极距分布非均一性的主要原因,极距的非均一性会造成4块阴阳极间的电阻的非均一性,导致阳极电流分布的非均一性,使得电解效率有所下降,因此极间间距的均匀分布很大程度上保障了槽体运行的不必要的能耗损失。依据本文所建立的二维数学模型,稀土电解槽左边的阳极一直处于消耗状态,而在模拟时槽体右边极距始终保持不变,因此建立槽体两边极距非均一性的评价指标,极距非均一性:

|
式中,r1为左方极距,r2为右方极距,r1=82.5、102.5、122.5、14.5 mm;r2=82.5 mm,则D∈[1,1.24,1.48,1.72]。
1.3 模型假设1)除槽内导电部分的电场之外,忽略其他额外设备的影响,且电场的分布不受磁场、热场、流场等物理场的影响;
2)电磁力较与气泡对电解质的驱动力可忽略不计;
3)熔体流动与析出的液态金属的流动对电场的影响,忽略不计。
2 几何模型及边界条件 2.1 几何模型本文在电场和温度场部分的计算使用ANSYS,流体计算使用FLUENT,以3 500 A上挂阴阳极式稀土电解槽的二维模型来模拟稀土电解过程。图 1所示为非均一极距下的几何模型。
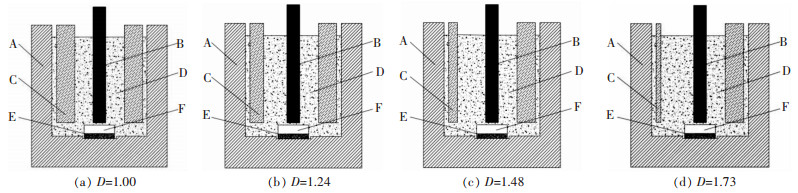 |
| 注:A: Refractory Brick; B: Cathode; C: Anode; D: Electrolytic; E: Rare Earth Metal; F: Crucible 图 1 几何模型 Fig. 1 Geometrical Model |
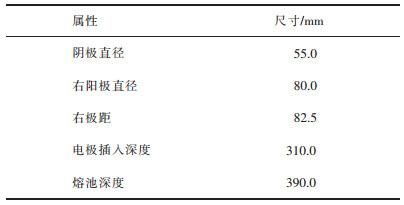
2.2 模型主要参数
电解槽模型规格的主要参数见表 1。
| 表 1 主要尺寸 Table 1 Main dimension |
 |
| 点击放大 |
2.3 边界条件
1)设阴极出口位置为零电势;
2)电极与外界环境的接触表面,设为第2类边界条件;电极与电解质的接触表面,设为第3类边界条件;
3)阳极表面定为速度入口,电解质上液面定为气体出口;
4)对于熔体而言,其他均为不可滑移壁面;其他流体边界对所有相界定为不可滑移壁面;
5)阳极表面释放的气泡主要成分为CO2和CO,假定CO2和CO的摩尔分数分别为a%和b%,气泡局部质量生成率[18-20]mloc(kgs-1m-2)可表示为:
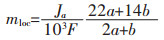
|
其中Ja为阳极电流密度(A/m2),F为法拉第常数。
3 计算结果与分析 3.1 不同非均一极距下电场分析图 2中可以看到4组不同D下的电位分布,图 2(a)中D值为1时,电位分布左右对称,阳极炭块和阴极金属棒各处电位相等,在阴极和阳极之间电位呈梯状分布;图 2(b)中随着左阳极半径的减小,左侧极间距增大使得D值增大,导致阴极左边区域电位分布梯度变小,两侧分布开始不对称;随着D值增大,图 2(c)、图 2(d)中阴极区电位向坩埚等势区左下方扩展,阴极下部区域电位变化幅度较大,容易增大电解质或金属的流动幅度,使阴极表面析出的金属液滴被冲刷回电解质中而被重新氧化,且电位向左下方偏移也会使金属滴落方向向左侧偏移,金属不能稳定落入槽底的坩埚中,使得稀土金属的收得率降低,影响实际生产作业的效率。
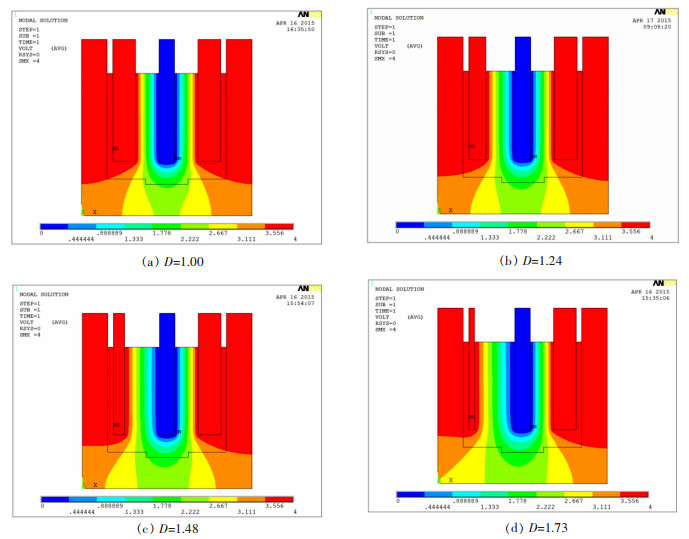 |
| 图 2 不同非均一性D下的电位分布 Fig. 2 The potential distribution of four different polar distance of D |
通过图 3的电流强度图知,在D=1时,图 3(a)中阴极两侧区域电流强度左右对称分布,且阴极区域的电流密度最大,往两侧逐渐减小,主要电流分布在双阳极间区域,在其他区域电流较小。随着左阳极厚度减小;图 3(b)中,D值增大,左侧极间距增大,右侧电流强度分布梯度较左侧更大,这与图 2(b)中D值增大,左侧电位梯度分布减小的的趋势一致;且随着D的增加,图 3(c)、图 3(d)中左侧极间电流持续减小,右侧阳极电流相应增大。使得右侧阴阳极间电解质区域的气泡含量增多,一定程度上降低了电流传输的效率。由于电解质自身的电阻率很大,在恒压的槽况中,D值增大导致了左侧极间距变大,极距部分的电阻随之变大,消耗了大量的电能,导致了一部分能耗的损失。
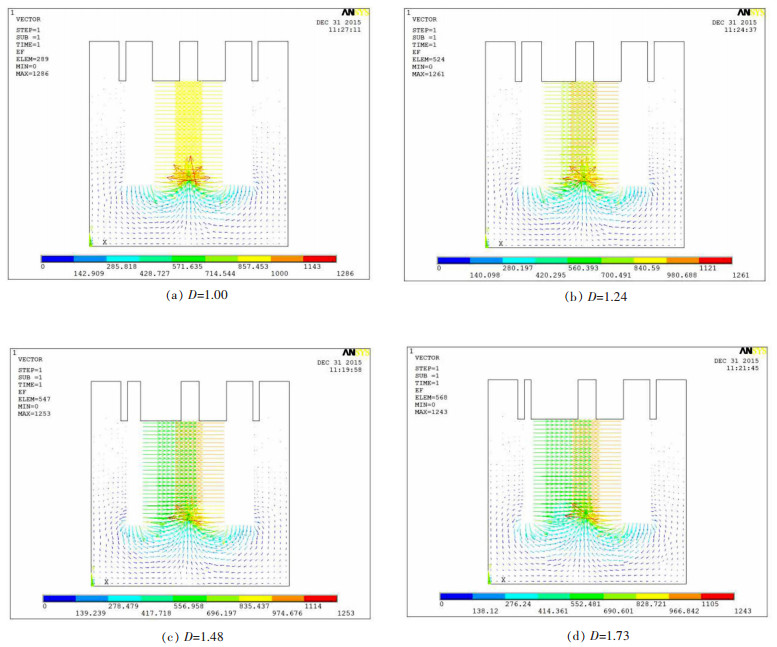 |
| 图 3 不同非均一性D下的电流强度 Fig. 3 Current intensity of four different polar distance of D |
从图 4中可以观察到由于总电压不变,在电解槽极距非均一性D逐渐变大的过程中,左右两边的阳极表面电流密度需要重新分配以达到平衡,因此阴极左侧区域的电阻值也有所增大。反之,电解槽右边的电阻减小,左方阳极电流密度逐渐降低,而右方阳极电流密度逐渐增大。且对比图 3中不同极距非均一性程度D下的不同电流强度的分布情况也不难看出,随着D的增大,左右极间的电流密度的差距也在增大,在图 4(d)中D=1.73时则达到了最大,此时对右侧阳极炭块的消耗速率也达到了最大,极大地影响了电解效率以及槽况的稳定。因此电解槽在此状况下需要停槽更换左方阳极,以稳定槽况,使电解槽继续稳定高效地电解生产。
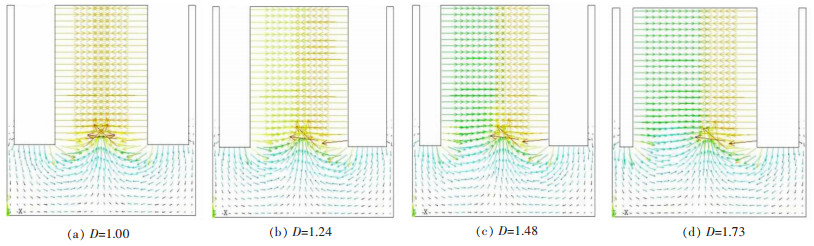 |
| 图 4 不同非均一性D下的电流密度 Fig. 4 Four different current density of D |
3.2 不同非均一极距下温度场分析
通过图 5的温度分布图可知,在D=1的模型中,高温集中在阴极附近,最高温度达到1 208 ℃,阴极阳极之间的温度呈递减趋势,由阴极向阳极区域形成均匀温度梯度,且阴极左右两边分布规律对称。随着左阳极半径减小,D值增大,阴极左边区域温度有所降低,D=1.24时最高温度降到1 120 ℃,D=1.48时最高温度为1 056 ℃,而D=1.73时最高温度仅为1 010 ℃,这与图 3中随着D值的增加,阴极左侧电流强度逐渐减小的分布规律相似。且高温区域向右方平移,且温度梯度变缓,从阴极区向坩埚区域扩散。说明D值的增大,变相增加了左侧极间的电阻率,在恒压电流的作用下,电阻率的增大,减少了温度的上升。
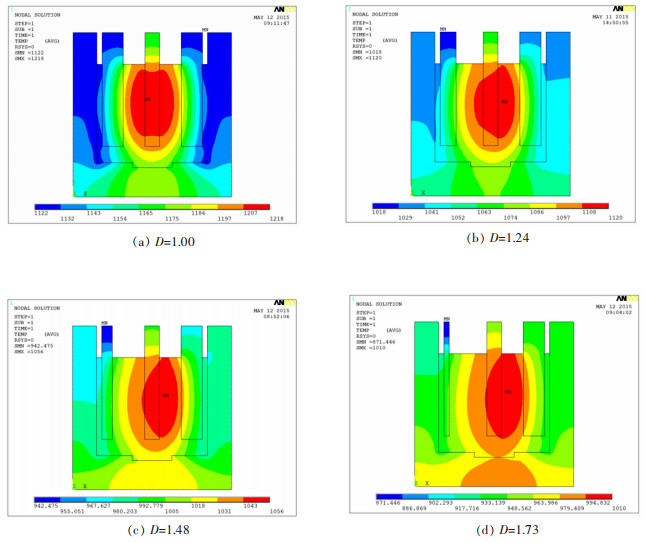 |
| 图 5 不同非均一性D下的温度分布 Fig. 5 Different temperature of four different polar distance of D |
3.3 不同非均一极距下气泡运动状态差异
从图 6不同极距非均一性D下气泡运动分布云图可以发现,随着D的增大,左边阳极表面生成的气泡量逐渐减少,而右边新阳极表面的气泡量逐渐增多,这是因为两端阳极为了平衡总电流,右侧阳极电流密度将会比D值为1时的电流密度大,导致气泡的生成量增大,因此阴极右侧极间的湍流强度变得更加剧烈,当非均一性D在1~1.48范围内增加时,右侧阳极表面的气泡尺寸逐渐增大,此状态下的气泡运动会影响阴极上析出的稀土,甚者将使阴极生成的稀土金属冲刷回电解质中再次氧化,降低收得率,如图 6(c)中D=1.48时,右侧极间电解质区域产生的大量气泡已经开始对阴极生成的金属进行扰动,将一部分金属液滴冲散,无法顺利回落入底部的坩埚中,造成一定程度的损失。但当极距非均一性D=1.73时,右边新阳极表面的气泡含量明显减少,原因是此时右边阳极表面产生的气泡积聚在阳极底部,导致阳极表面的气泡量也较少[21]。
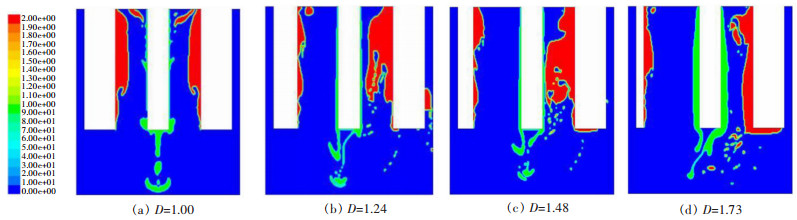 |
| 图 6 不同非均一性D下的气泡分布 Fig. 6 The distribution of bubble of four different D |
从图 7观察到当极距非均一性D在1~1.48范围内增加时,右边新阳极表面的气泡含量明显增多,当D值增大到1.73时,气泡含量有所减少,这是由于气泡生成速度过快,使得部分气泡在阴极下方开始堆积,同时增大了电解槽底部区域的湍流强度。从实际稀土电解过程中也可以发现,当两边的极距不相等时,右侧阳极与阴极间的气泡量明显大于左方阴阳极之间的气泡量,并且D值更大的阴阳两极间的气泡翻滚现象更严重,这种情况的出现不仅会影响槽内流体的流场分布,而且还会影响对生成的液相稀土金属的回收。
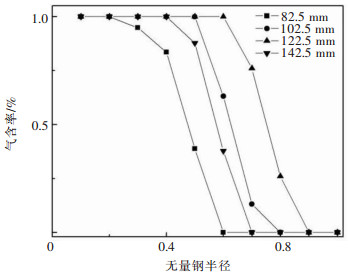 |
| 图 7 不同非均一性D下的径向极距气含率分布曲线 Fig. 7 The distribution curve of radial gas volume fraction of four different D |
3.4 不同非均一极距下流场的分布差异
从图 8不同极距下的流场分布图可以观察到,电解质的流动区域大部分处于阴阳极间以及阴极下端的区域,主要是由于气泡生成并逸出时的湍流,以及金属液滴生成后的缓慢流动,而气泡的流动速度较流动金属更大,体现为气泡的运动更为剧烈。而随着左边阴阳两极间的距离的增大,电解槽左方底部的紊流强度在极距非均一性D在1~1.48范围内增加时,是逐渐增强的,这与图 7不同非均一性D下径向极距气含率分布曲线图也是一致,即随着非均一性D的增加,新阳极表面的气泡量逐渐增多,将会促进槽内流场的流动,表现为槽内的紊流强度将会随非均一性D的增加而逐渐增强;但当极距非均一性D=1.73时,电解槽左方底部的流动强度降低,原因是此时新阳极表面电解产生的气泡部分积聚在阳极底部,导致阴阳极之间的湍流强度下降,从图 7中可以观察到当极距非均一性D=1.73时,槽内径向气含率降低到很低的值,表现为槽内流体的流动状况变得很差,这就表明当阳极反应到一定厚度时,即当非均一性D=1.73时,电流效率会迅速降低,此时不适合继续进行电解生产,需要停槽更换阳极,以稳定槽况,否则会增加电耗,降低稀土电解效率。
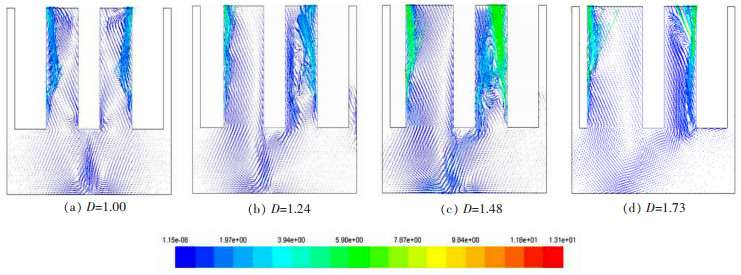 |
| 图 8 不同非均一性D下的流场分布 Fig. 8 The distribution of flow field of four different D |
图 9不同极距非均一性D下的径向湍流强度分布曲线表明,当极距非均一性D=1时电解槽内径向的湍流强度处于波动状态,因为此时电解槽内的流体大部分处于静止状态。流动状况较差,槽内各点还未稳定。当D=1.24~1.48时,槽内的径向湍流强度分布比较均匀,并且极距在此范围内时,湍流强度的值逐渐增大,这对应图 7不同非均一性D下径向极距气含率分布曲线中D在1.24~1.48下气含率在逐渐增大的现象是一致的,说明电解槽在此参数下的电解过程较稳定;但当极距非均一性D=1.73时,电解槽径向湍流强度小于极距非均一性D=1.24以下,这也与图 7不同极距下的径向气含率分布曲线图中出现气泡含量反而下降的规律一致,这说明电解槽极距非均一性D=1.73时,电流效率显著降低,使得阳极表面的电流密度降低到较低值,这表现为阳极表面的气泡量减少,导致槽内径向湍流强度降低。所以不同非均一性D下径向湍流强度的分布特征曲线图也表明当电解槽极距非均一性D=1.73时,需要立即更换阳极,避免槽况恶化。
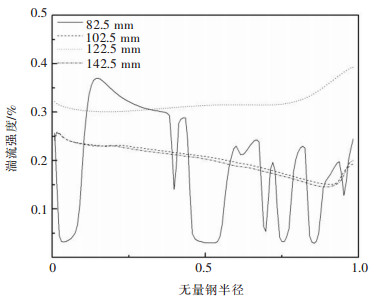 |
| 图 9 不同非均一性D下的径向湍流强度分布曲线 Fig. 9 The distribution curve of radial turbulence intensity of four different D |
3.5 不同非均一极距下金属液滴的分布差异
从图 10中可以发现当极距非均一性D在1.24~1.48范围内增加时,稀土金属相对于中心线偏移25°~30°,但对应图 6中稀土液相金属的运动轨迹来看,极距在此范围内的稀土金属还是能够顺利的滴落在坩埚里,所以在稀土电解生产过程中,当阳极消耗至此范围时,还可以继续生产;但当非均一性D=1.73时,阴阳两极间的湍流强度下降较低值,导致稀土金属黏附在阴极表面而不能快速地向电解槽底部下落,而积聚在阴极表面,所以此时的电流效率急剧下降,右方阳极的底部积聚了大量的气泡导致电解槽右方阳极底部的局部区域的流场过大,使得从阴极表面滴落的稀土金属与中心线呈43°向左方偏离,在图 6中也是表现出较大的偏角,此时电解出的稀土金属不能完全落入槽底的坩埚中,使得稀土金属的收得率降低,因此需要更换左方阳极,防止槽况的进一步恶化。
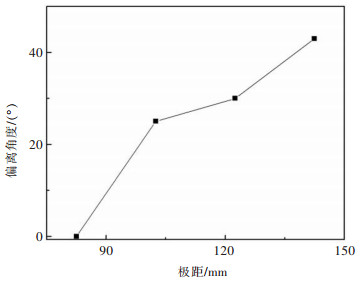 |
| 图 10 不同非均一性D下的稀土金属液偏离中心线角度分布曲线 Fig. 10 The distribution curve of the rare earth metals liquid offset from the centerline angle of four different D |
3.6 模型可靠性检验
等距压降法是电流通过阳极时,会有电压降的产生,对各阳极导杆进行固定长度区域压降的测量方法。在稀土电解槽电解过程中,各阳极导杆的横截面积是相等的,若温度条件保持不变,则可以认为阳极导杆等距压降是阳极电流的单值函数。因此阳极导杆等距电压降能反映出槽阳极的电流分布,通过对槽各阳极导杆的等距压降的测量,便可以实现对模拟的准确性进行检验。
图 11给出了稀土电解槽电解过程中4组不同D值对应的槽况下各阳极实际电流测量值与模拟电流值的对比情况,发现左阳极电流值随极距非均一性增大而减小,右阳极电流值随极距非均一性增大而增大。由于影响阳极电流大小的主要原因是新换阳极和极距,因为在新换阳极处,其阴阳极距大、电阻小,所以电流大;又因为4块阳极因消耗差异而导致更换时间不同,所以4块阳极与阴极间的极距不等,而导致阳极电流分布的不均匀。从数值上可以看出,实际电流测量值与电流模拟值的计算误差范围为2.7%~5.6%,由此证明了计算模拟的可靠性。
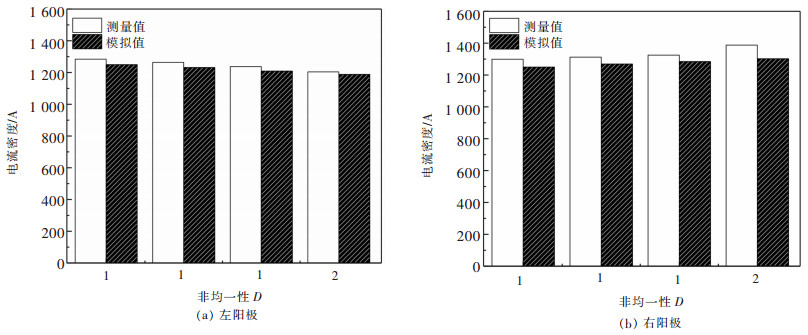 |
| 图 11 电解槽阳极电流测量值与模拟电流值 Fig. 11 The chart of current measured value and simulated value by FLUENT |
4 结论
1)与之前的模拟相比,本文模型考虑了极距非均一性对稀土电解的影响。结果表明,D值的改变对稀土电解过程中的电场、温度场、流场以及气泡的产生均有一定的影响,其中D=1.00~1.48。
2)随着D值增大,导致阴极左侧电位梯度、电流强度、电流密度下降,温度、热流密度降低,高温区向一侧偏移。研究表明,D值的增大使得电流效率下降,不利于稀土的产出。因此当D值达到一定数值需及时更换阳极,以提高电解槽的稳定性及生产效率。
3)当D=1时,电解槽径向的湍流强度处于波动状态;当D=1.24~1.48时,径向湍流强度增大;当D在1.00~1.48范围内时,阴极表面析出的稀土金属液在滴落的过程中,偏离电解槽中心线角度为0°~30°,此时可以落入槽底的坩埚内;当D=1.73,电解槽的径向气含率和径向湍流强度降低到较低的水平,并且稀土金属滴落时偏离中心线角度为43°,此时稀土金属便不能落入坩埚内。
4)利用等压极距法对稀土电解槽电流进行测试,结果表明,实际电流测量值与模拟电流值大体一致,因此通过数值模拟可以反映出极距非均一性对阳极电流分布不均的影响,为优化实际生产中的流程操作,提高电解效率,降低能耗提供保障。
| [1] |
SOLHEIM A, JOHANSEN S, THONSTAND J. Gas driven flows in Hall-Heroult cells[J].
J. Appl Electrochem, 1989, 19: 703–712. |
| [2] |
刘庆生, 汤卫东, 王建鲁, 等. 稀土电解槽内阳极气泡行为的数值模拟[J].
中国稀土学报, 2015, 33(6): 737–746.
|
| [3] |
BILEK M M, ZHANG W D, STEVENS F J.Modelling of electrolyte flow and its related transport processes in aluminium reduction cells[C]//In: Mannweiler U, eds.Light Metals, 1994.San Francisco, CA: TMS(The Minerals, Metals & Materials Society), 1994: 321-331.
|
| [4] |
姜艳丽, 郑奇, 喻亮, 等. 异型阴极结构铝电解槽热应力场仿真[J].
有色金属(冶炼部分), 2015(5): 37–42.
|
| [5] |
刘中兴, 李扬磊, 伍永福, 等. 电极插入不同深度下稀土电解槽电热场耦合模拟[J].
有色金属(冶炼部分), 2019(1): 31–36.
|
| [6] |
丁培林, 王恒, 黄俊, 等. 铝电解槽下料过程对电解质温度场的影响[J].
中国有色金属学报, 2016, 26(2): 430–438.
|
| [7] |
李贺松.
铝电解槽非稳态非均一信息模型及节能技术[M]. 北京: 冶金工业出版社, 2008.
|
| [8] |
FENG Y Q, COOKSEY M A, SCHWARZ M P. CFD modeling of alumina mixing in aluminium reduction cells[C]//HAGNIAM. Light Metals 2010. Seattle: TMS, 2010: 451-456.
|
| [9] |
伍永福, 张雪娇, 陈思琪, 等. 60 kA沉浸式稀土电解槽电场的数值模拟[J].
有色金属(冶炼部分), 2015(2): 31–33, 38.
|
| [10] |
MA H H, XUE J X, LI J G, et al. Investigating current efficiency of aluminum electrolysis in NaF-KF-AlF3 system[C]// Zhang Lifeng. Materials Processing Fundamentals. Hoboken, NJ, USA, 2013: 199-206.
|
| [11] |
逄启寿, 张雨开, 黄杰, 等. 稀土电解槽不同阴极结构的电解特性分析[J].
稀土, 2019(5): 17–23.
|
| [12] |
RAO J P, OUYANG C Y, LEI M S, et al. First principles investigation of interaction between interstitials H atom and Nb metal[J].
Acta Physica Sinca, 2012, 61(4): 1–5. |
| [13] |
董云芳, 冯猛, 刘中兴, 等. 稀土电解槽内双电层-温度场耦合数值模拟[J].
稀土, 2019(2): 88–94.
|
| [14] |
刘钊, 李宗安, 张小伟, 等. 稀土电解槽流场的数值模拟[J].
中国有色金属学报, 2015(11): 3209–3215.
|
| [15] |
GUPTA R K, NAYAN N, NAGASIREESHA G, et al. Development and characterization of Al-Li alloys[J].
Materials Science & Engineering A, 2006, 420(1/2): 228–234. |
| [16] |
刘冬福, 唐忠阳, 何利华, 等. 盐湖提锂膜堆电解槽流体水力学和数值模拟[J].
中国有色金属学报, 2019(2): 388–395.
|
| [17] |
ZHAN S Q, LI M Z, JIE M, et al. CFD simulation of effect of anode configuration on gas-liquid flow and alumina transport process in an aluminum reduction cell[J].
Journal of Central South University, 2015(7): 2482–2492. |
| [18] |
ZHAO C Y. Review on thermal transport in high porosity cellular metal foams with open cells[J].
International Journal of Heat and Mass Transfer, 2012, 55(13/14): 3618–3632. |
| [19] |
KRISTIAN E E. The Effect of detaching bubbles on aluminum-cryolite interfaces: An experimental and numerical investigation[J].
Metallurgical and Materials Transactions B, 2010, 41(3): 560–573. |
| [20] |
XU H B, HAN Q Y, THOMAS T. Effects of ultrasonic vibration on degassing of aluminum alloys[J].
Materials Science & Engineering A, 2008, 473(1/2): 96–104. |
| [21] |
SEVERO D S, GUSBERTI V, PINTO E C, et al. Modeling the bubble driven in the electrolyte as a tool for slotted anode design improvement[C]// SORLIE M. Light Metals 2007. Orlando, FL: TMS, 2007: 287-292.
|
 2020, Vol. 11
2020, Vol. 11


