| 基于LR-ANN-SVM的滑坡易发性评价 |
b. 江西理工大学,江西省矿业工程重点实验室,江西赣州 341000
b. Jiangxi Key Laboratory of Mining Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, Jiangxi, China
滑坡易发性评价是滑坡危险性评价的基础[1],所以滑坡易发性的科学划分与精度都至关重要。随着GIS与计算机算法的发展, 常见滑坡易发性评价模型为统计分析模型,其中简单的统计分析模型有信息量模型[2-4]、层次分析法[5-6]、证据权方法[7-8]等,但简单的统计分析模型在数据分析中存在着人为的主观性,并存在大量而繁重的工作,导致易发性评价精度较低。随着大数据的发展,为了解决人为的过度干预,并减轻地质灾害评价中的大量工作,大部分学者开始展开对复杂统计模型的研究。常见的复杂算法有逻辑回归模型[9-10],神经网络模型[11]与支持向量机模型[12]等。
本文以上犹县为研究区,首先根据遥感图像与实际调查获取滑坡易发性评价的影响因子,通过相关性分析,确定弱相关性的评价因子[13],并将各个评价因子进行分级,得到分级后的评价因子与上犹县历史滑坡单元建立上犹县灾害评价数据库。其次在滑坡单元数据500 m以外选取500个非滑坡单元,通过Arcgis空间连接得到上犹县滑坡单元与非滑坡单元的空间数据。考虑到存储空间与制图效果,确定栅格单元为30 m分辨率,将上犹县划分为1 717 906个栅格单元,得到每个栅格单元的空间数据,并对上述空间数据进行归一化处理[14]。最后将滑坡与非滑坡单元的空间数据随机分为80%作为训练集、20%作为测试集。上犹县栅格单元的空间数据作为预测集,输入逻辑回归模型、神经网络模型、支持向量机模型进行数据的训练、测试与预测,并利用自然断点法进行滑坡易发性等级的划分。为了提高易发性分区的安全性,将上犹县栅格单元取最大的易发性指数,即引入MAX(LSI(ANN), LSI(LG), LSI(SVM))将上述3种模型的易发性指数取最大值计算,提高高危险区与较高危险所包含的滑坡数。其具体流程如图 1所示。
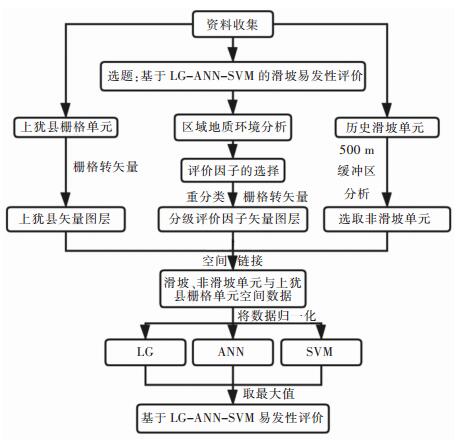 |
| 图 1 基于LG-ANN-SVM易发性评价流程 Fig. 1 Flow chart of evaluation of LG-ANN-SVM susceptibility |
1 滑坡易发性评价模型 1.1 逻辑回归模型
逻辑回归(LR)是一个二分类事件,将0设为非滑坡单元,1为滑坡单元[15]。逻辑回归(LR)揭示一个因变量与多个自变量的关系[16],能很好地解决二分类问题。并且LR模型的自变量分别为影响滑坡单元与非滑坡单元的评价因子。其公式如式(1)所示。
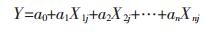
|
(1) |
式中:Y代表非滑坡与滑坡单元,取值为0或1;X1j, X2j,…,Xnj为各个评价因子的第j级别;a0, a1,…,an代表逻辑回归系数。若发生滑坡的概率用P来表示,其计算如下:
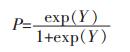
|
(2) |
在神经网络中,常见的算法有前馈神经网络[17](FNN)、反向传播算法[18](B-P)、多层感知器[19](MLP)。由于前馈神经网络是单项的多层结构,没有周期与循环,而MLP利用反向传播作为训练,又以前馈为连接,有多个隐藏层,算法复杂,对于数据的运算时间过长。所以本文选取反向传播算法(B-P)作为上犹县易发性评价的研究方法。假设各个评价因子用输入神经网络中的xi(i=1, 2, …, n)来表示,wi表示各个神经单元之间的权重,取特征函数为双向正切函数,其公式为:
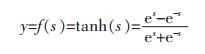
|
(3) |
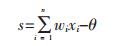
|
(4) |
式中:s代表神经元的输入总和;y代表神经元的输出;θ代表神经网络的阈值。
B-P神经网络是采用反向传播进行参数优化,调整权重。目的是使损失函数最小。假设神经网络的误差函数为Ep, 用来衡量B-P神经网络的能力。则其公式为:
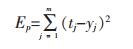
|
(5) |
SVM是将输入的数据映射在一个高维的空间,然后在此高维空间上进行线性分类,从而实现在原空间坐标系的非线性分类[20]。假设训练数据有n个,其表示为(xi,yi),其中xi表示评价因子,yi为表示是否为滑坡。只考虑一个变量,则支持向量机的超平面为:
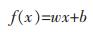
|
(6) |
式中:w为斜率:b为截距。当有n个数据输入,其超平面为:
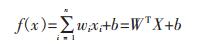
|
(7) |
式中:WT X为wixi的累加。在满足零均值与等方差的情况下,回归方程的参数用最小二乘法来确定,在保证输入变量的实际值与估测值的差值平方和达到最小的情况下,从而确定回归方程的系数,其公式如式(8)所示:
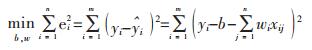
|
(8) |
式中:yi为在第i个因子观测的输出的预测值;(yi-ŷi)2(i=1, 2, …, n)是实际值与预测值相差的平方。设ε为不敏感函数,每个观测的误差函数都计入损失函数,进行叠加,当误差函数小于ε, 即误差可忽略不计[21]。本文将支持向量机的核函数选用线性核函数。
2 研究区概况上犹县位于江西省赣州市西部,坐标为东经114°~114°40′,北纬25°42′~26°01′,属于大陆性气候,平均气温18°。区内地势西高东低,常年多雨,灾害发育频繁。图 2为上犹县位置与灾害分布图。
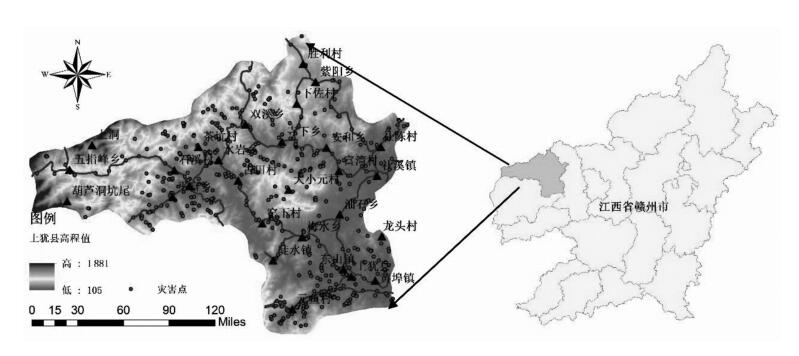 |
| 图 2 上犹县滑坡灾害分布 Fig. 2 Location of Shangyou County and distribution of landslide hazards |
通过调查在上犹县有滑坡点500个,其范围覆盖上犹县全境,最高的滑坡位于五峰山乡,其高度为200 m,为花岗岩岩性。由于大部分灾害围绕县城区域,在暴雨时期,这些滑坡可能酿成地质灾害,严重损害上犹县的经济发展。研究区内以构造侵蚀低山为主,主要有志留系、第四系、泥盆系、奥陶系、石炭系、三叠系与寒武系等地层组成,其岩性主要由粉砂岩、砾岩、细花岗岩、变辉长岩、砂岩、闪长岩、细粒辉长岩等组成。其次为构造中山,由花岗岩与组成,丘陵位于寒武系地层,由岩浆岩组成。侵蚀性岗地主要位于泥盆系,有岩浆岩等岩性组成。侵蚀性河谷主要有砂岩,有河流冲积形成。
3 指标因子的建立与分析文中滑坡易发性评价数据来源:①1:2 000上犹县地质灾害一览表;②地理数据云下载landsat5数据;③地理数据云下载的30 m分辨率得DEM数据;④上犹县1:20万地质图。
3.1 因子的选取通过对上犹县地质调查与水文分析,进行如下操作:①编写上犹县灾害调查表,从上犹县灾害调查表得:上犹县灾害点500个,通过GIS平台投影在上犹县图层。并对灾害点进行500 m的缓冲区分析,在缓冲区之外选取500个非滑坡单元作为机器学习的训练集与测试集。②基于GIS平台,分别从DEM数据获得:坡度、高程、坡向、水系、平面曲率、剖面曲率、湿度指数(TWI)、地形起伏度(SPI)、地表粗糙度(TRI)等栅格图。③将ladsat5TM数据band5与band4输入arcgis中,先对两波段栅格整型数据转化为浮点型, 然后运用arcgis的地图代数中的栅格计算器进行(band5-band4)/(band5+band4)运算,获取上犹县植被指数(NDVI)。④并将上述影响因子进行重分类,如图 3(a)~图 3(h)所示,将坡度分为0°~5°、5~9°、9°~12°、12°~16°、16°~20°、20°~25°、25°~30°、30°~37°、> 37°;坡向分为平面(-1)、北(0°~22.5°)、东北(22.5°~67.5°)、东(67.5°~112.5°)、东南(112.5°~157.5°),南(157.5°~202.5°)西南(202.5°~247.5°)、西(247.5°~292.5°)、西北(292.5°~337.5°)、北(337.5°~360°);平面曲率分为0~9、9~17、17~25、25~34、34~43、43~53、53~63、63~73、> 73;剖面曲率分为0~2、2~4、4~6、6~8、8~10、10~12、12~15、15~20、> 20;地形起伏度分为-71~-26、-26~-15、-15~-9、-9~-3、-3~1、1~6、6~13、13~22、> 22;地面粗糙度分为1~1.01、1.01~1.04、1.04~1.07、1.07~1.11、1.11~1.15、1.15~1.21、1.21~1.31、1.31~1.46、> 1.46;湿度指数分为2~6、6~9、9~21、21~35、> 35;植被指数划分为-0.34~0.17、0.17~0.40、0.40~0.53、0.53~0.62、> 0.62;⑤根据上犹县道路与水系进行欧氏距离分析,并利用重分类将道路缓冲区分为0~200 m、200~400 m、400~600 m、600~800 m、800~1 000 m、> 1 000 m; 将水系缓冲区分为0~100 m、100~200 m、200~300 m、300~400 m、400~500 m、> 500 m。⑥根据1:20万上犹县地质图,提取地层分布与断层,分别在Arcgis中做出如图 3(k)~图 3(l)所示,上犹县的地层由志留系、第四系、泥盆系、奥陶系、石炭系、三叠系与寒武系组成。对地质构造进行缓冲区分析,并进行重分类分为三类,分别为0~1 km、1~2 km、> 2 km。其最终评价因子与灾害点分布如图 3所示。
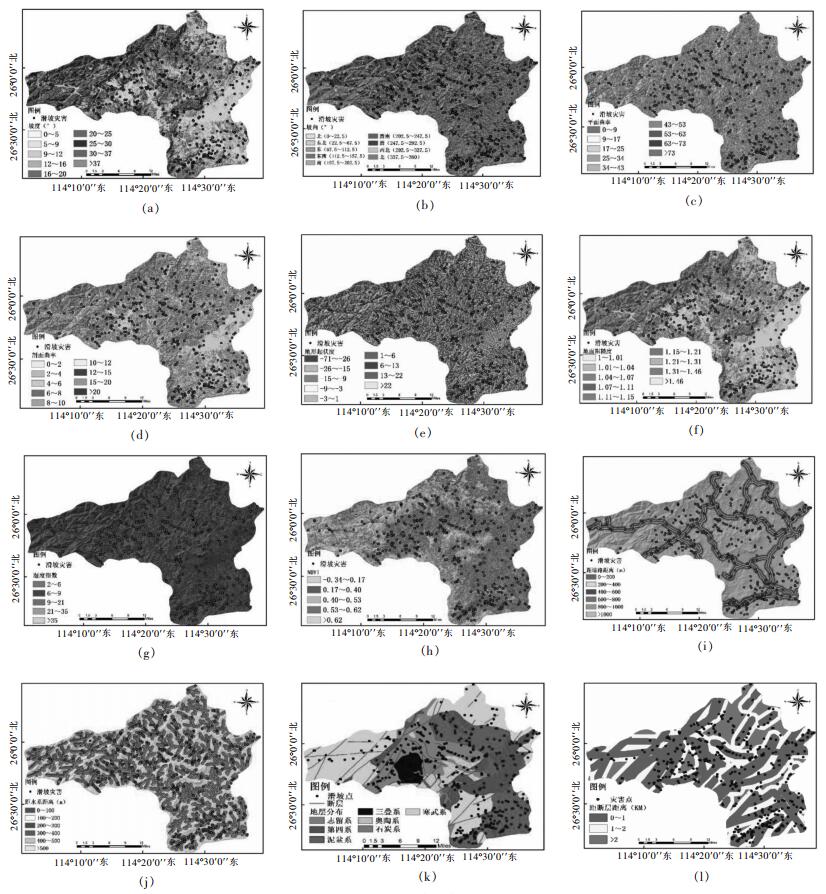 |
| 图 3 上犹县滑坡易发性评价因子 Fig. 3 Evaluation factors of landslide susceptibility in Shangyou County |
3.2 因子相关性分析
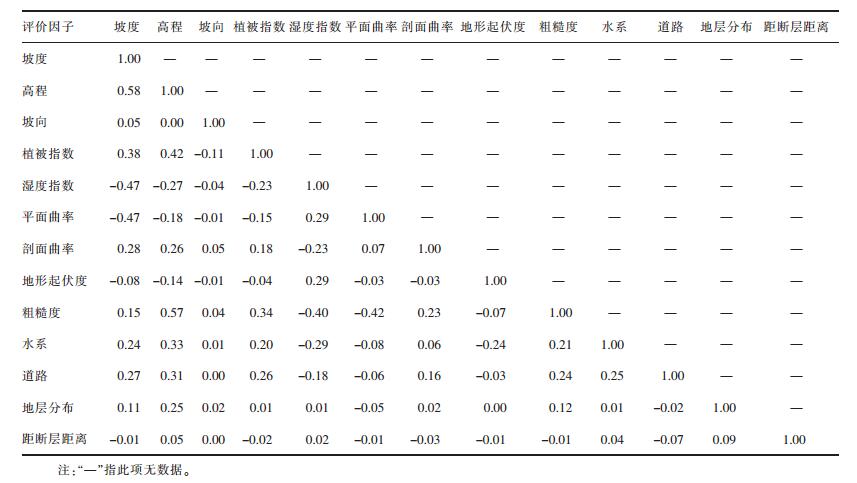
由于进行易发性评价过程中要保证数据之间不相关或弱相关,能有效地提高模型的效率。因此利用GIS的波段集统计,将上述评价因子栅格图层进行相关性分析。如表 1所列,由于高程与植被指数、水系、道路相关性大于0.3,且粗糙度与植被指数、湿度指数的相关性大于0.3,所以除去高程与粗糙度保证评价因子之间的不相关或弱相关。选取坡度、坡向、平面曲率、剖面曲率、地形起伏度、湿度指数、植被指数、距道路距离、距水系距离,地层分布与距断层距离等11个上犹县滑坡易发性评价因子。
| 表 1 波段集统计各因子相关性 Table 1 Correlation of various factors in band set statistics |
 |
| 点击放大 |
4 上犹县滑坡易发性评价 4.1 基于LR、ANN、SVM模型的易发性评价结果
对上犹县滑坡进行500 m缓冲区分析,在缓冲区以外选取500个非滑坡单元。将滑坡单元、非滑坡单元与11个评价因子图层进行空间连接,得到滑坡与非滑坡单元在上述评价因子空间数据,并将数据进行归一化。然后将滑坡单元与非滑坡单元的空间数据分为80%的训练集和20%的测试集,输入RapidMiner Studio进行逻辑回归、神经网络与支持向量机模型的训练与测试。为了保证模型的精度,采用交互验证法,挑选神经网络的训练次数120、学习率0.2、动量为0.1,支持向量机与逻辑回归模型采用默认参数。并将上犹县栅格单元所在空间归一化数据输入训练好的模型中,得出上犹县栅格单元的易发性指数,最后利用自然断点法将上犹县栅格的滑坡易发性指数进行重分类。如图 4所示,将上犹县分为高易发区、较高易发区、中易发区、较低易发区、低易发区。
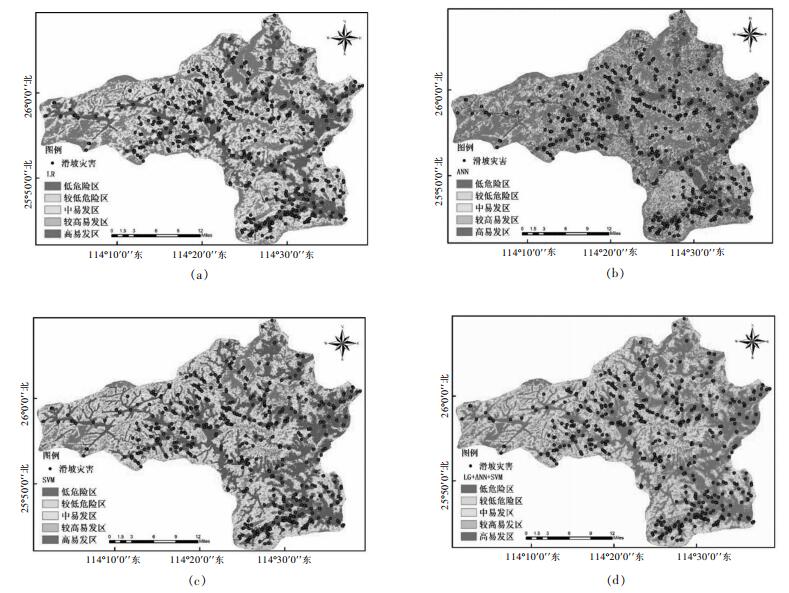 |
| 图 4 基于LR、ANN、SVM、LR-ANN-SVM的滑坡易发性分区 Fig. 4 Landslide susceptibility zones based on LR, ANN, SVM and LR-ANN-SVM |
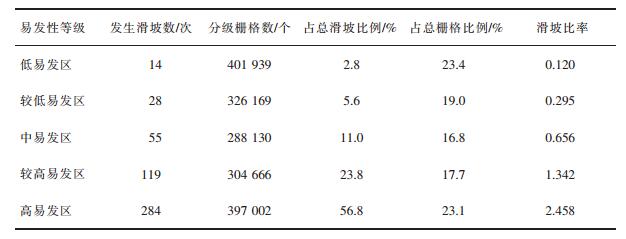
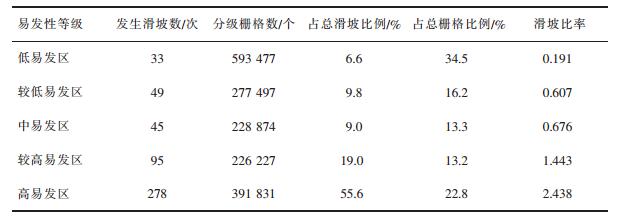
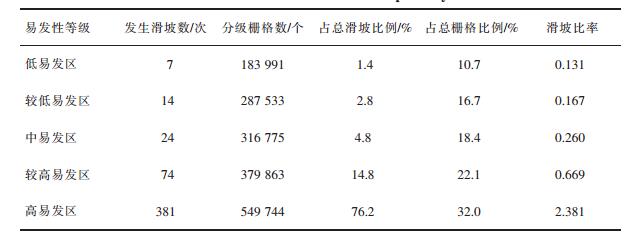
统计上述模型易发性分区的灾害数与栅格数,并计算出占总滑坡数比例、占总栅格数比例、滑坡比率,得表 2、表 3、表 4。如表 2、表 3与表 4所示:LR、ANN、SVM的易发性分区的高易发区与较高易发区所包含的滑坡单元占比分别为80.6%、74.6%、91%,SVM的高易发区所包含的灾害占比最高,针对该区域进行重点滑坡灾害治理,可以更好地控制上犹县滑坡灾害。高易发区的面积占比能很好地衡量在易发性分区的科学性,根据统计表显示:LR、ANN、SVM的高易发区占比分别为23.1%、22.8%、32.0%,都占比较小,符合上犹县的实际情况。滑坡比率是滑坡比例与易发区占比的比值,衡量分类最优化,保证高易发区与较高易发区的滑坡密度最大。由统计表显示:LR、ANN、SVM模型的高易发区的滑坡比率分别为2.458、2.438、2.381,都有较大的滑坡比率,而且随着易发性分区从高到低滑坡比率逐渐减小,符合滑坡易发性从高易发区到低易发区的分区结果。
| 表 2 逻辑回归易发性统计表 Table 2 Statistics of logistic regression susceptibility |
 |
| 点击放大 |
| 表 3 神经网络易发性统计表 Table 3 Statistics of neural network susceptibility |
 |
| 点击放大 |
| 表 4 支持向量机易发性统计表 Table 4 Statistics of SVM susceptibility |
 |
| 点击放大 |
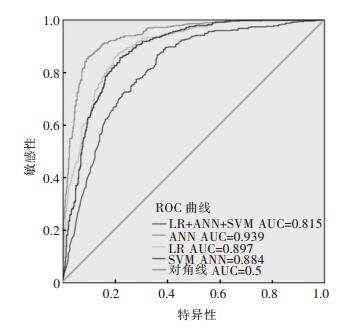
文章通过受试者工作曲线(ROC)进行模型的精度评价,ROC的评定模型精度的标准用曲线下的面积(AUC)来衡量。AUC > 0.5时,当AUC越接近1,其精度越高。AUC在0.5~0.7之间说明其精度差,AUC在0.7~0.9之间精度较好,AUC在0.9~1之间精度很好,AUC < 0.5则不符合客观事实[22]。将训练所得到的易发性指数与训练数据一起输入SPSS中,通过ROC分析得如图 5,横轴为特异性,纵轴为敏感性。如图 5所示,LR、ANN、SVM的AUC值分别为0.897、0.939、0.884,都大于0.8,证明模型有较好的评价精度。其中神经网络模型有最高的评价精度。
 |
| 图 5 上犹县滑坡易发性评价ROC曲线 Fig. 5 ROC curve of landslide susceptibility evaluation in Shangyou County |
4.2 基于LR-ANN-SVM模型的易发性评价结果
为了上犹县栅格单元的安全性,引入滑坡发生的预警值来衡量滑坡的易发性,即要在滑坡发生之前进行预警,所以选取3种模型评价上犹县栅格单元易发性的最大值来当栅格发生滑坡的可能性,其公式为:
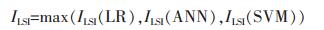
|
(9) |
式中,ILSI为易发性指数,MAX取LR、ANN、SVM易发性指数的最大值。将式(9)所得的易发性指数导入上犹县栅格,得到基于LR-ANN-SVM模型的上犹县栅格单元易发性指数。最后将上犹县栅格单元滑坡易发性指数进行重分类,得如图 4(d)所示的上犹县易发性评价分区图。
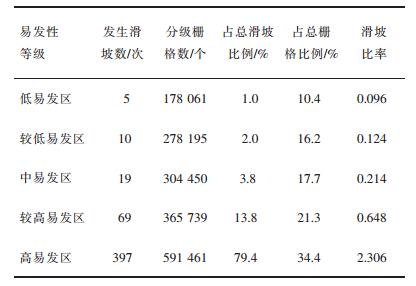
高易发区所包含的灾害比例能反映模型评价的科学性,将更多的灾害单元包含在高与较高易发区更方便政府部门的治理。根据表 2、表 3、表 4、表 5统计可知,LR、ANN、SVM、LG-ANN-SVM的高易发区与较高易发区所包含的灾害占总灾害比例分别为:80.6%、74.6%、91%、93.2%。结果显示LR-ANN-SVM易发性分区的高易发区有更高的滑坡灾害比例,低危险区灾害比例占比为1%,此分区更适用于上犹县风险性的实际应用,如图 5 ROC曲线下的面积(AUC)所示,LR-ANN-SVM的AUC值为0.815,说明LR-ANN-SVM评价模型有很好的评价精度。
| 表 5 LR-ANN-SVM易发性统计表 Table 5 Statistics of LR-ANN-SVM susceptibility |
 |
| 点击放大 |
4.3 易发性结果分析
综合上述4种模型易发性分区结果分析,其高危险区多在水系、县城附近,以及泥盆系与志留系地层上,河水的冲刷能带走压坡脚的土之外,还会增加土壤的含水率,使滑动面的摩擦力减小,导致滑坡更容易产生。县城附近是人类工程活动导致植被的破坏,植被指数较低,并且城镇附近道路较多,在修建的过程中,难免会削坡,导致坡度的增加,破坏土体的稳定性,从而产生了滑坡。最终分类结果与上犹县历史滑坡实际情况相符。
5 结论1)以上犹县为研究区,对滑坡编录数据进行分析,利用相关性分析确定评价因子。通过LR、ANN与SVM模型进行上犹县滑坡易发性评价。并利用受试者工作曲线(ROC)对上述模型进行精度评价,结果显示LR、ANN、SVM的AUC值分别为0.897、0.939、0.884,3个模型都有较好的易发性评价精度。
2)为了上犹县栅格单元的安全性,引入预警值来对上犹县滑坡易发性进行分析,将预警值取为上述3个模型得出的上犹县栅格易发性指数的最大值,结果显示LR-ANN-SVM模型易发评价的AUC值为0.815,有很好的评价精度。从高易发区与较高易发区滑坡占比来看,LR、ANN、SVM、LR-ANN-SVM高易发区与较高易发区所包含的滑坡占总滑坡比例为80.6%、74.6%、91%,93.2%,LR-ANN-SVM所包含的灾害比例最高,且低易发区灾害点占比仅含1%。通过预警能很好地进行滑坡灾害治理,减少上犹县滑坡灾害发生的概率。
3)高易发区与较高易发区位于道路与城镇附近,植被发育相对薄弱的地带,并随着水系呈带状分布。与上犹县历史滑坡的实际情况相符,可作为上犹县灾害治理的科学依据。
| [1] |
夏辉, 殷坤龙, 梁鑫, 等. 基于SVM-ANN模型的滑坡易发性评价——以三峡库区巫山县为例[J].
中国地质灾害与防治学报, 2018, 29(5): 13–19.
|
| [2] |
王佳佳, 殷坤龙, 肖莉丽. 基于GIS和信息量的滑坡灾害易发性评价——以三峡库区万州区为例[J].
岩石力学与工程学报, 2014, 33(4): 797–808.
|
| [3] |
安凯强, 牛瑞卿. 信息量支持下SVM模型滑坡灾害易发性评价[J].
长江科学院院报, 2016, 33(8): 47–51.
|
| [4] |
杨盼盼, 王念秦, 郭有金, 等.基于加权信息量模型的临潼区滑坡易发性评价[J/OL].长江科学院院报: 1-9[2020-02-10].
|
| [5] |
任敬, 范宣梅, 赵程, 等. 贵州省都匀市滑坡易发性评价研究[J].
水文地质工程地质, 2018, 45(5): 165–172.
|
| [6] |
陈飞, 郭顺, 熊如宗, 等. 基于层次分析法的地质灾害危险性评价[J].
有色金属科学与工程, 2018, 9(5): 54–60.
|
| [7] |
王珂, 郭长宝, 马施民, 等. 基于证据权模型的川西鲜水河断裂带滑坡易发性评价[J].
现代地质, 2016, 30(3): 705–715.
|
| [8] |
郭长宝, 唐杰, 吴瑞安, 等. 基于证据权模型的川藏铁路加查——朗县段滑坡易发性评价[J].
山地学报, 2019, 37(2): 240–251.
|
| [9] |
饶运章, 张学焱. 基于Logistic回归模型确定权重的模糊综合评判法在边坡稳定性分析中的应用[J].
有色金属科学与工程, 2015, 6(6): 111–115.
|
| [10] |
刘艺梁, 殷坤龙, 刘斌. 逻辑回归和人工神经网络模型在滑坡灾害空间预测中的应用[J].
水文地质工程地质, 2010, 37(5): 92–96.
|
| [11] |
AGHDAM I N, VARZANDEH M H M, PRADHAN B. Landslide susceptibility mapping using an ensemble statistical index (Wi) and adaptive neuro-fuzzy inference system(ANFIS) model at Alborz Mountains (Iran)[J].
Environmental Earth Sciences, 2016, 75(7): 553. |
| [12] |
ZHOU C, YIN K, CAO Y, et al. Application of time series analysis and PSO-SVM model in predicting the Bazimen landslide in the Three Gorges Reservoir, China[J].
Engineering Geology, 2016, 204: 108–120. |
| [13] |
HUANG F, YIN K, HUANG J, et al. Landslide susceptibility mapping based on self-organizing-map network and extreme learning machine[J].
Engineering Geology, 2017, 223: 11–22. |
| [14] |
贾丽娜.基于GIS的永靖县滑坡易发性制图[D].兰州: 兰州大学, 2019.
|
| [15] |
栗泽桐, 王涛, 周杨, 等. 基于信息量、逻辑回归及其耦合模型的滑坡易发性评估研究:以青海沙塘川流域为例[J].
现代地质, 2019, 33(1): 235–245.
|
| [16] |
ERENER A, MUTLU A, DUZGUN H S, et al. A comparative study for landslide susceptibility mapping using GIS-based multi-criteria decision analysis(MCDA), logistic regression (LR) and association rule mining(ARM)[J].
Engineering Geology, 2016, 203: 45–55. |
| [17] |
黄发明.基于3S和人工智能的滑坡位移预测与易发性评价[D].武汉: 中国地质大学, 2017.
|
| [18] |
WANG L J, GUO M, SAWADA K, et al. A comparative study of landslide susceptibility maps using logistic regression, frequency ratio, decision tree, weights of evidence and artificial neural network[J].
Geosciences Journal, 2016, 20(1): 117–136. |
| [19] |
唐晓娜.基于卷积神经网络和综合指数模型的吕梁市滑坡灾害易发性评价[D].太原: 太原理工大学, 2019.
|
| [20] |
黄发明, 殷坤龙, 蒋水华, 等. 基于聚类分析和支持向量机的滑坡易发性评价[J].
岩石力学与工程学报, 2018, 37(1): 156–167.
|
| [21] |
SU C, WANG L, WANG X, et al. Mapping of rainfall-induced landslide susceptibility in Wencheng, China, using support vector machine[J].
Natural Hazards, 2015, 76(3): 1759–1779. |
| [22] |
杜国梁, 张永双, 吕文明, 等. 基于加权信息量模型的藏东南地区滑坡易发性评价[J].
灾害学, 2016, 31(2): 226–234.
|
 2020, Vol. 11
2020, Vol. 11


