| 复配添加剂在硅酸二钙表面吸附性能的耗散粒子动力学模拟 |
碱石灰烧结法生产氧化铝是处理低品位含铝原料提取氧化铝的最有效工艺之一,其中氧化铝烧结熟料溶出过程是决定氧化铝提取效率的重要环节。在溶出过程中,熟料中硅酸二钙(β-C2S)组分可与铝酸钠溶液中NaOH、Na2CO3和NaAl(OH)4相互作用,使熟料中已经溶出的Al2O3和Na2O转化为水化石榴石和钠硅渣沉淀,造成Al2O3和Na2O损失[1-2],该过程称为二次反应。近年来研究与生产实践发现,添加高分子聚合物添加剂来抑制二次反应提高氧化铝溶出率是很好的方法[3-4]。添加剂可以通过化学键或物理作用吸附在硅酸二钙表面,在固体表面上形成一层吸附膜,减少硅酸二钙表面与溶液接触,从而抑制硅酸二钙分解、降低二次反应的发生。
近年来,聚合物添加剂抑制熟料溶出二次反应的研究很多, 其中多数是关于单一添加剂的抑制效果及机理研究[5-17]。关于多种添加剂复配使用抑制二次反应的研究不多,只有张程忠研究聚合物PAAS与PEG复配使用的抑制效果[18]。研究发现聚合物PAAS与PEG复配添加较单一添加聚合物PAAS或PEG具有更好地抑制效果和更少的添加量,其中以质量比为1:1条件下的复配效果最好。但是对于复配聚合物之间的协同作用机理缺乏研究。
耗散粒子动力学(DPD)是连接微观与宏观的一种很好的介观模拟方法,可以从介观的角度上揭示聚合物在固体表面的吸附过程。本文在前期研究工作的基础上,采用耗散粒子动力学方法研究聚合物PAA与PEG复配添加剂在硅酸二钙表面的吸附行为,从介观的角度探讨复配添加剂的协同作用效果及其机理,研究结果将为新型复配添加剂的开发提供理论依据。
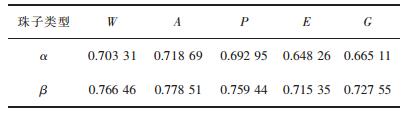
1 DPD方法及参数 1.1 粗粒化为了进行DPD模拟,首先对体系中的聚合物PAA和PEG以及水分子进行粗粒化处理。如图 1所示,聚合物PAA由珠子A构成,一个珠子A代表一个丙烯酸单体;PEG由3种珠子组成,聚合物长链的两端分别为珠子P和珠子G,链的中间为珠子E;另外将3个水设定成一个珠子。因为这些珠子都拥有近似的体积,确保了模拟计算的准确性。聚合物链长设置为50,根据聚合物的结构建立PAA(A50)和PEG(P1E48G1)长链。
 |
| 图 1 粗粒化处理示意 Fig. 1 Coarse granulation |
1.2 耗散粒子动力学
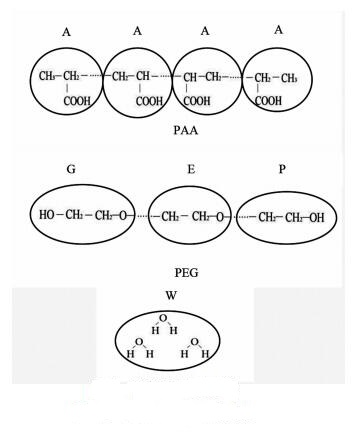
在耗散粒子动力学中,作用在每个珠子i上的总力为[19]:
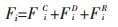
|
(1) |
式(1)中:Fic、FiD、F iR分别表示保守力、耗散力和随机力。耗散力和随机力的耦合遵循涨落耗散定理。此外, 一对珠子相互作用的Fi是遵循牛顿第三定律,因此动量守恒。这在更大的尺度上产生了正确的水动力行为。总力Fi对势能的保守贡献包括键和非键贡献。对于拉伸和角度势,采用谐波形式,不考虑扭转或面外扭转。非键的相互作用是纯排斥的、软的、短范围内的,其表达式由下面特定的公式给出:
|
(2) |
式(2)中:r是珠子i与j之间的距离;rDPD是非键相互作用阶段半径,由珠子的种类获得。DPD相互作用参数aij的量纲作为能量。对于聚合物和水,其最初的珠子数密度设置为3rDPD-3, 因此给出rDPD=0.646 nm[20]。使用的DPD时间单位表示为tDPD=rDPD(m/kT)1/2。由于惯性效应并不影响模拟结果,因此所有珠子的质量被认为是相等的,计算时可以用粗粒度实体质量的加权平均值来计算。DPD珠子相互间存在软排斥作用,为了防止聚合物珠子可能渗透到硅酸二钙底层,在DPD模拟中,硅酸二钙的密度设置为溶液密度的5倍,为15rDPD-3。
非键聚合物珠子之间的相互作用计算分为两部分:中性珠子作用aij*及成对珠子之间的相互作用(与Flory-Huggins参数xij成比例)。通过下面的式子来计算相同类型珠子之间的相互作用[21]:
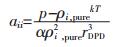
|
(3) |
式(3)中:aii是相同类型珠子之间的相互作用参数;ρi,pure是珠子i的纯液体数密度;p是设置的压强;a是方程中的状态常数,当数密度大于3时,a=0.101。不同珠子具有不同的纯液体密度,这将得到不同的aii值。
通过推导具有可变摩尔体积的珠子间热力学性质与DPD参数之间的比例关系,得到液态不同种类珠子之间的相互作用计算式子[22],如式(4)所示:
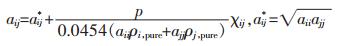
|
(4) |
对于液相珠子i与硅酸二钙固体界面的相互作用参数ais,通过匹配DPD密度剖面的表面过剩吸附量与MD密度剖面的表面过剩吸附量。表面过剩吸附量Γ是用来量化珠子在表面的吸附,表征不同珠子的相对吸附特性[23-24]。
首先,从分子动力学(MD)仿真模拟计算每个分子单体所对应珠子的表面过剩吸附量Γ值,Γ的计算关系式如下[23]:
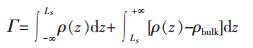
|
(5) |
式(5)中:p(z)和pbulk分别是珠子在Z轴方向上的数密度和体相密度;LS是表面的坐标,如图 2。在MD模拟中,定义为硅酸二钙中最后一个原子的中心加上van der Waals半径。考虑到不同的体相密度,文中采用更好的值Γ′=Γ/pbulk,其能够更好地描述界面层的长度和宽度。
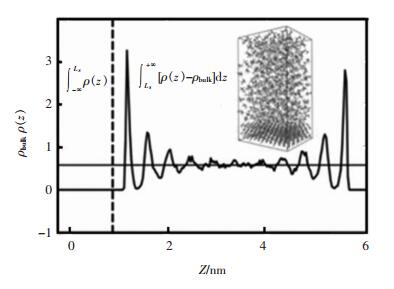 |
| 图 2 MD模拟纯液体在硅酸二钙表面的数密度分布 Fig. 2 MD simulated number density distribution of pure liquid on the surface of dicalcium silicate |
其次,对每一种珠子类型,设置不同的ais进行DPD模拟,计算其分别对应的Γ′值,做DPD模拟中的Γ′与ais的函数关系式。最后通过匹配MD和DPD模拟下得到的Γ′值获得适宜的珠子i与表面间的ais值。其中DPD中选取合适的LS的值对匹配结果影响非常大,在文中选用硅酸二钙表面在S轴方向上最后一个珠子的中心位置(i.e., 2rDPD)加上一个非键相互作用的阶段半径(i.e., 2rDPD)。
1.2.1 DPD模拟细节构建链长为50的聚合物珠子,并建立大小为(15×15×19)rDPD-3的盒子,在盒子的顶部和底部分别构建一层硅酸二钙珠子层,厚度为2rDPD,将硅酸二钙基底的笛卡尔坐标固定,只有溶液液相的珠子波动,其中液相珠子含有10 125个,压强设为p=38.7 rDPD-3kT。在模拟过程中,盒体的波动小于0.9%,对数量密度的影响可以忽略不计。时间步长设为0.005tDPD,总的模拟时间设置为(2×103)tDPD,第1个(1×103)tDPD用于体系平衡,后面的用于数据采集。
1.2.2 MD模拟细节MD模拟采用MS8.0软件,使用COMPASSⅡ力场。首先通过无机晶体结构数据库(ICSD)建立尺寸为4.669 4 nm×4.367 5 nm×1.981 5 nm的含有(110)晶面的β-C2S。每一种珠型的分子液体都是分别以完整的原子细节创建的。液体的初始结构是由Amorphous Cell模块构成的。能量优化后,选择NPT系宗,压强为1.013 25×105 Pa,温度为353 K条件下放松体系使其还原液体本来密度。将构建的含液相的不定型混合晶胞置于超晶胞(110)晶面上,构建纯液相/β-C2S体系初始模型。
选择NPT系宗,时间步长为1 fs,模拟总时间为1 ns,温度为353 K,采用Eward加和方法处理静电力和范德华力,截断半径为12.5 nm,模拟期间固定硅酸二钙的位置。
2 结果和讨论 2.1 聚合物和水与硅酸二钙的DPD相互作用参数文中计算了聚合物和水与硅酸二钙相互作用的DPD参数。如前文所述,每种类型的珠子与硅酸二钙表面相互作用的ais都有一个唯一的Γ′值与之一一对应。最后得到了每种类型珠子与硅酸二钙表面相互作用参数ais与Γ′值的关系趋势曲线,如图 3。通过幂次函数曲线拟合来描述该趋势曲线,得到的幂次函数拟合参数列入表 1中。
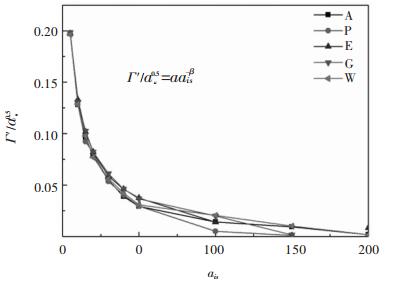 |
| 图 3 表面过剩吸附量与液固间相互作用参数ais的关系曲线 Fig. 3 Relationship curve between the excessive adsorption amount on the surface and the interaction parameter ais |
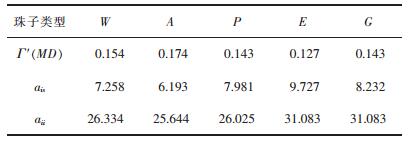
然后,通过Γ′(MD)=Γ′(DPD)来计算得到每种珠子与硅酸二钙固体界面的DPD参数ais。表 2中列入了每种类型珠子MD计算得到的表面过剩吸附量Γ′(MD),并计算出每种珠子与硅酸二钙固体界面的DPD参数ais。
| 表 2 MD模拟的表面过剩吸附量(Γ′(MD)),液相珠子与硅酸二钙表面的DPD相互作用参数(ais),相同类型珠子之间的相互作用DPD参数(aii) Table 2 MD simulation of excess surface adsorption quantity (Γ'(MD)), liquid phase on the surface of the beads and dicalcium silicate DPD interaction parameters (ais), and the interaction between the same types of beads DPD parameters (aii) |
 |
| 点击放大 |
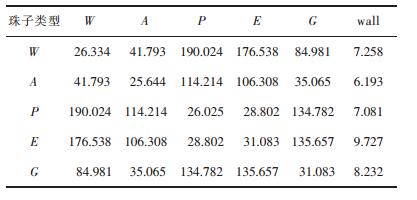
ais是液相珠子i与硅酸二钙固体表面的排斥参数,ais值越大,表明液相珠子与硅酸二钙表面的排斥力越大,越不利于吸附;相反,ais值越小,表明液相珠子与硅酸二钙表面的亲和力越强,越有利于吸附。由表 2中ais值可以看出各种液相珠子与硅酸二钙表面有较高的亲和力,其中丙烯酸(A)单体的珠子亲和力最高。丙烯酸官能团(珠子A)能与硅酸二钙表面的钙离子螯合形成离子键,羟基官能团(珠子P)能与硅酸二钙表面形成氢键,因此珠子与硅酸二钙有很高的亲和性是合理的。将文中DPD模拟中涉及的相同珠子之间斥力参数aii、不同珠子之间斥力参数aij,以及珠子与硅酸二钙壁之间的斥力参数ais列入表 3。
| 表 3 DPD中所用的斥力参数aii,aij和ais Table 3 Repulsion parameters aii, ai and ais used in DPD |
 |
| 点击放大 |
2.2 DPD模拟平衡判断
体系的平衡可以通过聚合物的扩散系数的波动来确定。一般,聚合物扩散系数的波动范围在10%以内,就可以代表体系达到了平衡[24]。以PAA为例,图 4所示为链长为50的10%浓度聚合物PAA的扩散系数波动曲线,可以看出在2 ns以后体系中聚合物的扩散系数在(0.2±0.02)×10-9 m/s范围内波动,因此可以判断体系在2 ns时达到平衡。
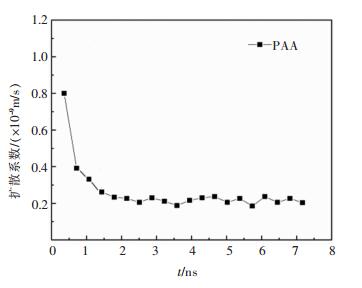 |
| 图 4 10%浓度,链长为50的聚合物PAA在体系中的扩散系数与时间的关系 Fig. 4 Relationship between diffusion coefficient and time of polymer PAA with chain length of 50 at 10% concentration |
2.3 密度分布
水溶液环境中聚合物添加剂与水分子在硅酸二钙表面存在竞争吸附,聚合物的吸附直接影响硅酸二钙表面水分子的分布。聚合物与硅酸二钙表面吸附相互作用越强,其在溶液中的密度分布越接近硅酸二钙表面,排除硅酸二钙表面水分子能力就越大,就越易在硅酸二钙表面形成吸附层,从而更好地阻碍液相与硅酸二钙表面接触,实现抑制硅酸二钙分解的目的[25]。根据文献的实验条件(张程忠的研究[13]),本文选定PAA与PEG的质量浓度配比条件分别为8:2(PAA8:PEG2)、5:5(PAA5:PEG5)以及2:8(PAA2:PEG8)进行模拟研究。
图 5和图 6所示分别是聚合物浓度为10%的条件下,吸附平衡后,聚合物在硅酸二钙表面的密度分布图以及水在硅酸二钙表面的密度分布图。
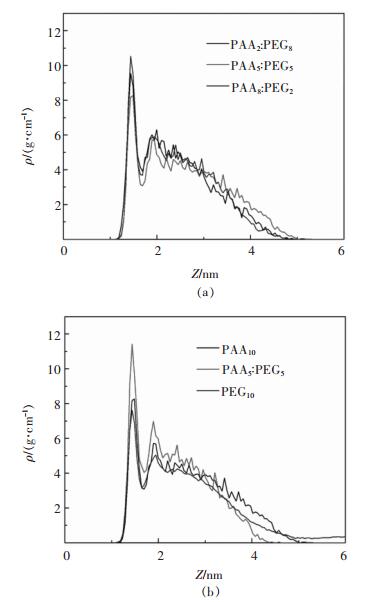 |
| 图 5 10%浓度条件下,聚合物在硅酸二钙表面的密度分布 Fig. 5 The density distribution of polymer on the surface of dicalcium silicate at 10% concentration |
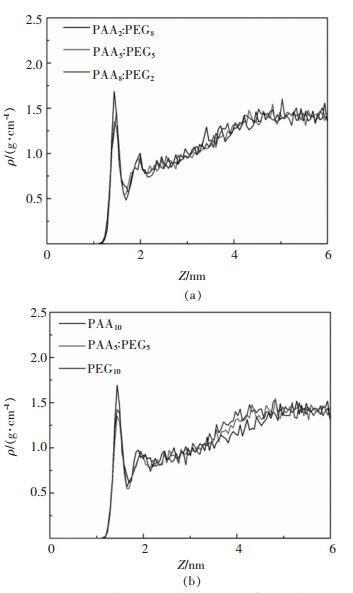 |
| 图 6 10%浓度条件下,水在硅酸二钙表面的密度分布 Fig. 6 The density distribution of water on the surface of dicalcium silicate at 10% concentration |
从图 5(a)中对比聚合物在距离硅酸二钙表面1~2 nm内的密度分布的峰值,可以看出PAA和PEG在不同的质量浓度配比条件下,聚合物峰值PAA5:PEG5>PAA8:PEG2>PAA2:PEG8,说明聚合物PAA与聚合物PEG在5:5复配条件下,复配聚合物在硅酸二钙表面吸附量最多,效果最好。同理,对比图 5(b)中聚合物在距离硅酸二钙表面1~2 nm内的密度峰值,可以看出聚合物吸附效果PAA5:PEG5>PAA10>PEG10,表明PAA5:PEG5复配添加剂在硅酸二钙表面的吸附效果比单一添加剂PAA、PEG要好。
对比图 6(a)中在距离硅酸二钙表面1~2 nm内水密度分布的峰值,可以看出PAA和PEG在不同的质量浓度配比条件下,水分子在硅酸二钙表面的峰值PAA2:PEG8>PAA8:PEG2>PAA5:PEG5,说明聚合物PAA与聚合物PEG以5:5的质量浓度比复配条件下,水分子在硅酸二钙表面的水分子最少,意味着复配聚合物PAA5:PEG5与硅酸二钙表面作用最强,驱替水分子的效果较好。同理,对比图 5(b)中距离硅酸二钙表面1~2 nm内的水密度峰值,PAA5:PEG5复配添加剂对应的水的密度峰值最低,表明PAA5:PEG5复配添加剂的吸附效果与单一添加剂的好。
综上所述,PAA5:PEG5复配添加剂在不同浓度配比的复配添加剂中吸附效果和驱替硅酸二钙表面水分子的能力较好,且效果优于单一聚合物添加剂PAA10和PEG10,与试验结果一致。
2.4 吸附稳定性吸附层的扩散系数可以表征吸附层在硅酸二钙表面的稳定性,扩散系数越大,表明吸附层分子在硅酸二钙表面运动越剧烈,越不利于阻碍铝酸钠溶液与硅酸二钙表面接触,抑制硅酸二钙分解的效果就越差。均方位移(DMSD)是一种确定分子随时间的移动方式的方法,利用均方位移可以表征分子自由扩散、运输以及束缚程度,均方位移计算式为:
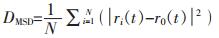
|
(6) |
式(6)中:N是分子个数;ri(t)代表t时刻分子的坐标;r0(t)代表分子初始时刻的坐标。分子的扩散系数D与均方位移的关系,可以由Einstein关系式获得[22-23],即式(2),分子的扩散系数越大表明其扩散能力越大。
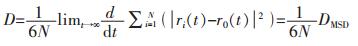
|
(7) |
文中绘制了吸附平衡后,聚合物吸附层的均方位移图并计算了其自扩散系数,如图 7及表 4所示。
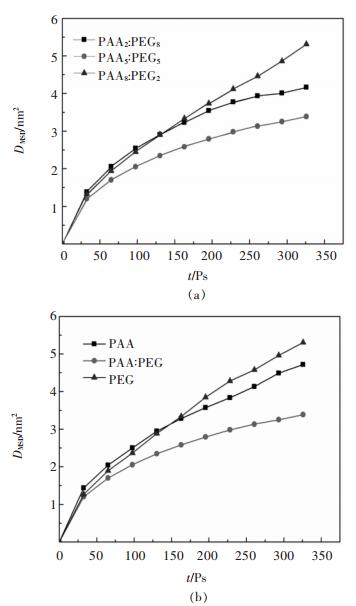 |
| 图 7 聚合物在溶液体系中的均方位移 Fig. 7 Mean azimuth shift of polymer in solution system |
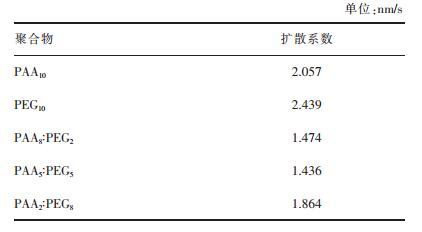
| 表 4 聚合物吸附层的扩散系数 Table 4 Diffusion coefficient of polymer adsorption layer |
 |
| 点击放大 |
对比表 4中聚合物吸附层的扩散系数,任一复配添加剂的扩散系数都小于单一添加剂的扩散系数,可以看出聚合物PAA与PEG复配能够提高聚合物在硅酸二钙表面的稳定性,其中PAA5:PEG5复配添加剂吸附层在硅酸二钙表面的扩散系数最低,说明其在硅酸二钙表面吸附稳定性最好,与试验结果一致。
2.5 吸附过程图 8所示为PAA5:PEG5复配聚合物吸附在硅酸二钙表面的过程,为了方便观察,图中隐去水珠子。图 8中上下两层为硅酸二钙,紫色代表珠子A,白色代表珠子P,蓝色代表珠子E,红色代表珠子G。如图 8所示,开始时(0 ns),聚合物PAA和聚合物PEG随机分布在水溶液中,体系处于随机分布状态;随着模拟时间的增加,在聚合物珠子之间相互作用下,溶液中的聚合物PAA和聚合物PEG相互聚集形成胶束,只有少量PAA的珠子吸附在硅酸二钙表面。随着时间的推移,珠子与硅酸二钙表面之间的相互作用开始占主导,溶液中PAA聚合物胶束先吸附在硅酸二钙表面,然后带动PEG聚合物胶束接近表面并吸附;在2 ns以后达到吸附平衡状态,两种聚合物相互交缠地紧密地吸附在表面。从整个吸附过程可以看出,聚合物PAA和聚合物PEG之间相互作用,彼此携带,具有明显的协同促进吸附的作用。
 |
| 图 8 PAA5:PEG5复配聚合物吸附快照图(隐去水珠子) Fig. 8 Adsorption snapshot diagram of PAA5:PEG5 composite polymer (water stripping beads) |
3 结论
1)本文采用多尺度联合方法,通过对比MD与DPD表面过剩吸附量确定介观模拟中聚合物、水及固相间的作用参数,实现了介观与微观尺度之间的耦合。计算的聚合物PAA和PEG在硅酸二钙表面吸附排斥参数表明聚合物珠子可以吸附在硅酸二钙表面上,这与实际中聚合物在硅酸二钙表面的吸附性能一致。
2)对比不同比例复配聚合物以及水在硅酸二钙表面的密度分布,可以看出,聚合物PAA与PEG为5:5复配表现出更强的吸附效果和驱替硅酸二钙表面水分子的能力。
3)较优复配聚合物与同等浓度的单一添加剂PAA、PEG对比,PAA5:PEG5复配添加剂吸附效果、驱替水分子的能力以及自身吸附稳定性皆强于单一添加剂PAA、PEG。结果表明,PAA5:PEG5复配聚合物之间存在协同作用,其抑制硅酸二钙分解的效果较优。
本实验可为复配添加剂在烧结法生产氧化铝工艺实践生产中的应用提供理论基础。
| [1] |
毕诗文. 氧化铝生产工艺[J].
北京:化学工业出版社, 2006.
DOI: 10.3724/SP.J.1095.2012.00057.
|
| [2] |
杨重愚. 轻金属冶金学[J].
北京:冶金工业出版社, 2014.
DOI: 10.3969/j.issn.1007-0958.2010.05.011.
|
| [3] |
王亮. 提高熟料净溶出率的措施[J].
轻金属, 2015(6): 19–22.
|
| [4] |
权昆, 武福运. 铝酸钠溶液中硅酸二钙的分解及抑制[J].
有色矿冶, 2005, 21(2): 29–34.
|
| [5] |
尤晶.添加剂抑制熟料溶出二次反应的研究[D].沈阳: 东北大学, 2005.
|
| [6] |
任根宽. 二次反应抑制剂及其添加工艺技术研究[J].
轻金属, 2008(5): 16–18.
|
| [7] |
刘欣.添加剂抑制熟料溶出二次反应的研究[D].沈阳: 东北大学, 2008.
|
| [8] |
张玉衡.新型抑制熟料溶出二次反应抑制剂的合成及其抑制机理研究[D].赣州: 江西理工大学, 2019.
|
| [9] |
康立武.烧结法熟料溶出过程中抑制二次反应的研究[D].赣州: 江西理工大学, 2010.
|
| [10] |
张程忠, 于海燕, 李光柱, 等. PEG对烧结法熟料溶出过程二次反应的影响[J].
轻金属, 2007(12): 13–15.
|
| [11] |
张程忠, 于海燕, 董宝才, 等. 聚合物AY在硅酸二钙-铝酸钠溶液体系中的吸附和分布[J].
轻金属, 2008(2): 48–52.
|
| [12] |
丁婷婷.表面活性剂在β-2CaO·SiO2界面吸附行为热力学与电化学研究[D].沈阳: 东北大学, 2011.
|
| [13] |
YU H Y, PAN X L, DiNG T T, et al. Adsorption of sodium polyacrylate at interface of dicalcium silicate-sodium aluminate solution[J].
Transactions of Nonferrous Metals Society of China, 2011, 21(10): 2323–2326. DOI: 10.1016/S1003-6326(11)61015-7. |
| [14] |
刘涵.聚合物在硅酸二钙表面吸附的分子动力学研究[D].沈阳: 东北大学, 2011.
|
| [15] |
佟志芳, 胡斌, 肖成, 等. 聚丙烯酸在硅酸二钙表面吸附的分子动力学模拟[J].
有色金属科学与工程, 2016, 7(6): 25–29.
|
| [16] |
TONG Z F, XiE Y B, ZHANG Y H. Molecular dynamics simulation on the interaction between polymer inhibitors and β-dicalcium silicate surface[J].
Journal of Molecular Liquids, 2018, 259: 65–75. DOI: 10.1016/j.molliq.2018.03.018. |
| [17] |
TONG Z F, ZHANG Y H, XiE Y B. interaction mechanism between copolymer inhibitor and β-dicalcium silicate surface based on molecular dynamics simulation[J].
Molecular Physics, 2020, 118(2): 1–11. |
| [18] |
张程忠.抑制熟料二次反应添加剂的研究[D].沈阳: 东北大学, 2008.
|
| [19] |
HOOGERBREGGE P J, KOELMAN J M V A. Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics[J].
Europhys Leet, 2007, 19(3): 155. DOI: 10.1209/0295-5075/19/3/001. |
| [20] |
KACAR G, PETER E A J F, WiTH G D. Mesoscopic simulations for the molecular and network structure of a thermoset polymer[J].
Soft Matter, 2013, 9(24): 5785. DOI: 10.1039/c3sm50304f. |
| [21] |
KACAR G, PETER E A J F, WiTH G D. A generalized method for parameterization of dissipative particle dynamics for variable bead volumes[J].
Europhys Leet, 2013, 102(4): 40009. DOI: 10.1209/0295-5075/102/40009. |
| [22] |
KACAR G, PETER E A J F, WiTH G D. Structure of a thermoset polymer near an alumina substrate as studied by dissipative particle dynamics[J].
The Journal of Physical Chemistry C, 2013, 117(40): 21028. DOI: 10.1021/jp409106m. |
| [23] |
刘亮. 2-MBI与SDBS协同缓蚀机理的实验与分子模拟研究[D].北京: 中国石油大学, 2015.
|
| [24] |
ALDER B J, GASS D M, WAiNWRiGHT T E. Studies in molecular dynamics. VIII. the transport coefficients for a hard log phere Fluid[J].
Chem Phys, 1970, 53(10): 3813–3826. |
| [25] |
CAO B Y, DONG R Y. Nonequilibrium molecular dynamics simulation of shear viscosity by a uniform momentum source-and-sink scheme[J].
Journal of Computational Physics, 2012, 231(16): 5306–5316. DOI: 10.1016/j.jcp.2012.04.017. |
 2020, Vol. 11
2020, Vol. 11