| 新一代溶液几何模型改进及应用 |
2. 省部共建高品质特殊钢冶金与制备国家重点实验室,上海200444;
3. 北京科技大学冶金与生态工程学院,北京100083;
4. 钢铁冶金新技术国家重点实验室,北京100083
2. State Key Laboratory of Advanced Special Steel, Shanghai 200444, China;
3. School of Metallurgical and Ecological Engineering, University of Science and Technology Beijing, Beijing 100083, China;
4. Skate Key Laboratory of Advanced Metallurgy, Beijing 100083, China
冶金熔体是冶金物理化学研究的对象,分为金属熔体、冶金熔盐和冶金熔渣三大类[1]。随着科学技术的发展,对冶金熔体的物理化学性质需求日益迫切。如何在已有的实验基础上,以最少的投入、最短的时间去填补这一大片的数据空白是当下急需解决的难题。目前,采用理论模型计算的方法是解决这一难题的最为行之有效的方法。
当前的理论模型可划归为物理模型[2]和唯象模型[3]两大类。前者是在物质的结构基础上提出的,根据量子力学和统计力学的原理估算出熔体的物理化学性质。这类模型虽然能够给出清晰的物理图像但其运用范围较窄,准确度也相对较差。后者则是一种半理论半经验的方法,它将理论和具体数据相结合,推导出应用范围较广的计算公式,其物理意义虽不如物理模型那样明确,但却能够给出更加合理的预测数据,在目前冶金熔体物理化学性质数据的估算过程中被广泛应用。
几何模型[4]是基于二元系数据的一种半理论半经验的模型。它作为最具代表性的唯象模型,已成为当前多元系合金物化性质估算和相图计算的主要方法。根据二元系成分点的选点方式的不同,将传统几何模型分为对称模型和非对称模型两大类[5],其中最具代表性的对称模型有Kohler(1960)[6]、Muggianu(1975)[7]以及Luck-Chou(1987)等[8]几种模型。非对称模型则包括Toop(1965)[9]、Hillert(1980)[5]等几种模型。但无论是对称模型还是非对称模型都存在较大的问题,例如对称模型的“还原问题”,以及非对称模型中“非对称组元”的选取问题等[10]。
1 改进模型的提出为了解决上述几何模型存在的问题,在第23、24届国际相图会议—CALPHAD年会上,周国治提出了新一代溶液几何模型[11],模型的推导过程见文献[12]。新一代溶液几何模型由于引入了相似系数和偏差函数的概念,解决了对称模型的还原问题,同时避免了非对称模型中所存在的人为干预的缺陷。新一代溶液几何模型打破了对称模型和非对称模型的界限,它是一个高度概括的普遍化模型,换句话说成百上千种的对称模型和非对称模型都是新一代溶液几何模型的特例。
包括新一代溶液几何模型在内的所有几何模型都有一个共同的特点——它们都建立了二元系代表点和多元系点之间的函数关系,如式(1)所示,这也就是通常所说的“选点方式”。新一代溶液几何模型的“选点方式”如图 1所示,模型种类的不同归根到底在于选点方式的不同。
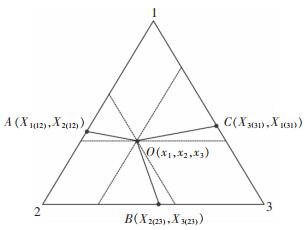 |
| 图 1 新一代溶液几何模型的“选点方式”示意 Fig. 1 The "selection method" of new general solution model |
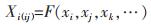
|
(1) |
在利用几何模型预测三元系性质的过程中,通常是根据3个已知的二元系代表点的性质去预测相应三元系点的性质,这一思路其实是具有局限性的。仅考虑3个二元系代表点的性质是远远不够的,应该将包括3个二元系代表点在内的邻近区间范围内所有二元系点的性质也一并考虑在内。二元系点性质对三元系点性质的“影响程度”可按照两点在成分三角形中的位置确定,即两点之间距离越小,则“影响程度”越大。而正态分布函数则是实现这一“影响程度”具体化的最佳函数,图 2所示为正态分布曲线表示“影响程度”的示意图。
 |
| 图 2 正态分布曲线表示“影响程度”的示意 Fig. 2 The normal distribution curve indicates the "degree of influence" |
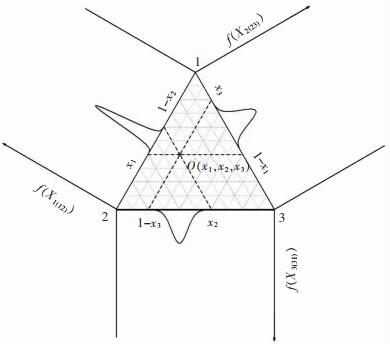
i-j二元系边界点(Xi(ij), 1-Xi(ij))的性质对任意三元系点(xi, xj, xk)的性质的“影响程度”,可表示为:
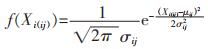
|
(2) |
式(2)中Xi(ij)为组元i在i-j二元系中的摩尔分数,对于参数σij和μij的取值可用三元系成分xi,xj,xk来确定。其中μij与三元系成分的关系可表示为:
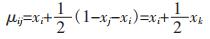
|
(3) |
表示“影响程度”的正态分布函数,其半高宽2.355σij可与三元系成分建立如下关系:
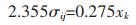
|
(4) |
明确了三元系成分与二元系成分在正态分布函数中的关系后,将函数引入到新一代溶液几何模型当中,改进后的模型如式(5)所示。
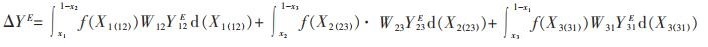
|
(5) |
式(5)中的ΔYE和YEij分别为三元系和二元系的超额物化性质,改进模型是在新一代溶液几何模型的基础上,在每一项的权重因子Wij之前乘以相应的f(Xi(ij)),再逐项积分,最终加和得到三元系的超额物化性质。图 3所示为改进模型预测三元系物化性质的计算流程图,图 3中二元系的超额物化性质YEij的函数表达式是基于实验数据得到的。
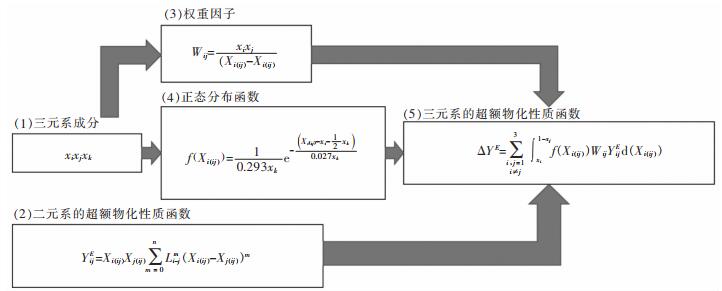 |
| 图 3 改进模型的计算方法流程 Fig. 3 Flow pattern of calculation method of modified model |
相较于原模型(未加入分布函数的新一代溶液几何模型),改进模型打破了往常仅根据几个已知的二元系代表点的性质推测多元系性质的局限性,将二元系代表点邻近区间内所有点的性质和多元系点的性质联系在了一起。从“选点方式”的角度来看,与原模型相比,改进模型更具有优势。为此,文中通过文献调研,收集了大量关于金属熔体物化性质的实验数据,选取了实验数据较为全面的In-Sn-Zn和Ag-Bi-Sn这两个体系进行计算来证明这一点。在下文中将通过原模型和改进模型分别对在不同温度、不同成分条件下两个体系的物化性质进行预测,并与实验数据进行对比,最后讨论计算结果。
2 模型应用及计算结果的讨论 2.1 In-Sn-Zn合金物化性质的预报Behera等[13]采用电动势法系统地测试了In-Sn-Zn三元合金在813 K下In:Sn为1:2、1:1和2:1三个截面处组元Zn的活度以及偏摩尔超额吉布斯自由能,并根据式(6)达肯方程[14]计算得到了In-Sn-Zn相应截面的全摩尔超额吉布斯自由能。
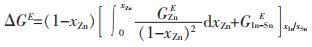
|
(6) |
Redlich-Kister(R-K)表达式[15]是二元系热力学性质常用的一种表达方法,
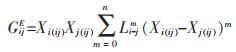
|
(7) |
式(7)中: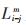
| 表 1 In-Sn-Zn三元系合金液相热力学参数 Table 1 Thermodynamic parameters for the liquid phase of In-Sn-Zn ternary alloy |
 |
| 点击放大 |
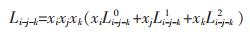
|
(8) |
基于三元系合金的液相热力学参数,运用原模型和改进模型,可获得In-Sn-Zn三元液态合金的过剩吉布斯自由能值。根据式(9)和式(10),可进一步获得组元Zn的局部热力学性质。
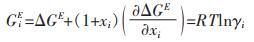
|
(9) |
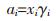
|
(10) |
式(9)中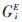
针对文献中报道的实验值进行点对点的计算,为更好地验证模型的预报效果,我们引进了对平均偏差Δ的计算,其定义为:
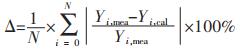
|
(11) |
式(11)中,N为总数据量,Yi,mea、Yi,cal是计算值和实验值。In-Sn-Zn三元系合金的全摩尔超额吉布斯自由能,组元Zn的偏摩尔超额吉布斯自由能以及活度的计算值与实验值的对比结果如图 4~图 6所示。
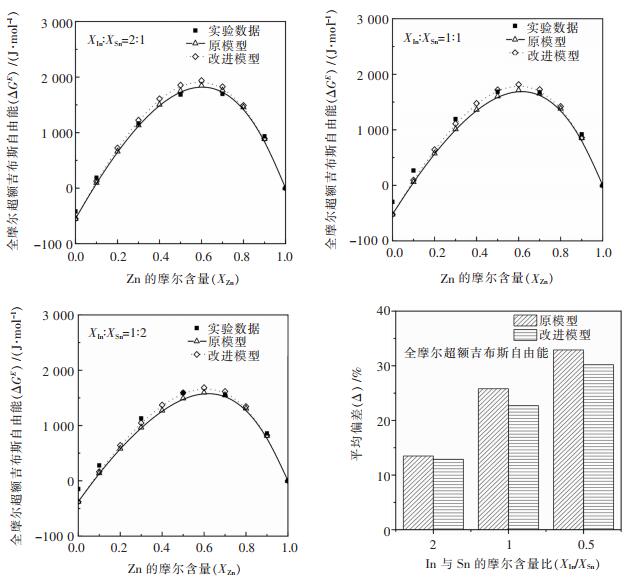 |
| 图 4 813 K下In-Sn-Zn体系全摩尔超额吉布斯自由能计算值与参考文献值的比较结果 Fig. 4 Comparison of integral molar excess Gibbs free energy between theoretical models and literature data at 813K for In-Sn-Zn alloys |
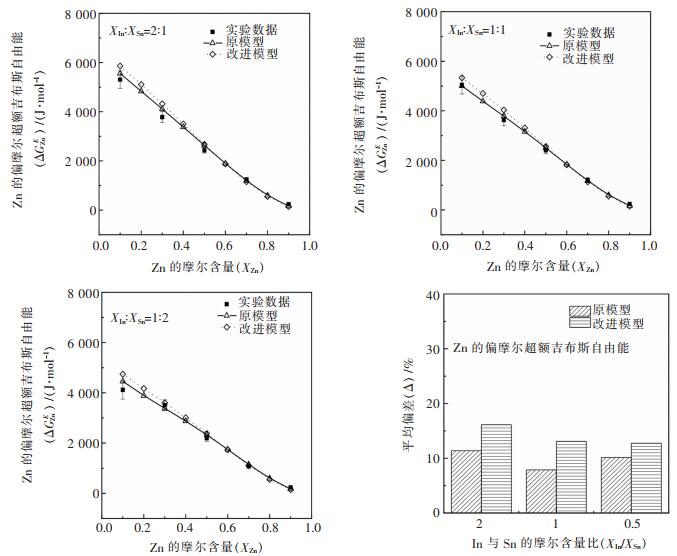 |
| 图 5 813 K下In-Sn-Zn体系中组元Zn的偏摩尔超额吉布斯自由能计算值与参考文献值的比较结果 Fig. 5 Comparison of partial molar excess Gibbs free energy of zinc between theoretical models and literature data at 813 K for In-Sn-Zn alloys |
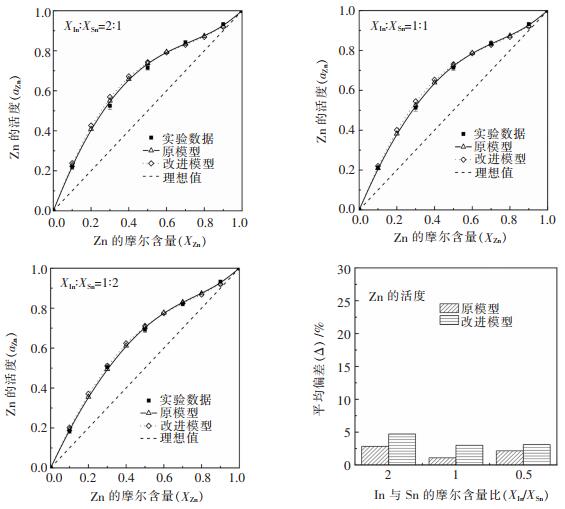 |
| 图 6 813 K下In-Sn-Zn体系中组元Zn的活度计算值与参考文献值的比较结果 Fig. 6 Comparison of activity of zinc between theoretical models and literature data at 813 K for In-Sn-Zn alloys |
通过观察图 4可以发现在所研究的温度范围下,大部分浓度范围内的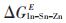
从Zn的偏摩尔超额吉布斯自由能的对比结果来看,实验值和预测曲线的变化趋势是一致的,Zn含量小于50%时,实验值和预测值存在适度偏差。针对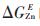
在整个浓度范围内,所研究截面处组元Zn的活度与理想值均呈正偏差。实验点与预测曲线均拟合较好,两条预测曲线在Zn浓度为0.1~0.5之间出现轻微偏差,其余部分几乎重合。针对aZn的计算,原模型的平均偏差在1%~3%,改进模型的平均偏差在3%~5%。
Pstrus[22]采用膨胀计量法系统地测试了In-Sn-Zn三元合金在523 K下In:Sn为1:3、1:1和3:1三个截面处的合金密度,并用气泡最大压力法测试了相应合金的表面张力。由于模型是利用二元系性质来预测三元性质的,因此计算的准确性和二元系数据的精度以及二元系数据分析处理的方式是密不可分的,Redlich-Kister表达式(以下简写为R-K表达式)是目前处理这类数据使用的较好的经验式。赵飞等[23]基于3个二元系KCl-CaCl2、MgCl2-CaCl2、KCl-MgCl2的密度数据,采用R-K表达式拟合得到了它们的超额密度函数;严丽君等[24]通过R-K表达式拟合得到了Ni3S2-FeS、FeS-Cu2S、Cu2S-Ni3S2三个二元系相应的超额表面张力函数。二元系In-Sn,Sn-Zn和Zn-In的密度数据和表面张力数据分别取自文献[25-27],同样采用R-K表达式拟合相应二元系的超额函数,In-Sn、Sn-Zn和Zn-In的超额表面张力函数和超额密度函数如表 2、表 3所列。图 7分别是R-K表达式对各二元系超额表面张力和超额密度的拟合结果。
| 表 2 23 K下In-Sn、Sn-Zn和Zn-In超额表面张力函数 Table 2 Excess surface tension of In-Sn, Sn-Zn and Zn-In binary alloy at 523 K |
 |
| 点击放大 |
| 表 3 523 K下In-Sn、Sn-Zn和Zn-In超额密度函数 Table 3 Excess density of In-Sn, Sn-Zn and Zn-In binary alloy at 523 K |
 |
| 点击放大 |
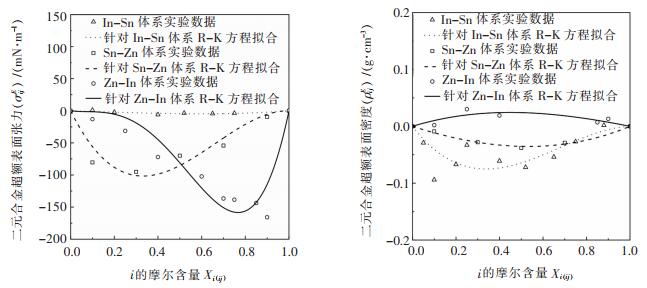 |
| 图 7 R-K方程对In-Sn-Zn合金二元系超额表面张力和密度的拟合结果 Fig. 7 Fitting results of excess surface tension and density of In-Sn-Zn alloy binary system by R-K equation |
三元系的物化性质与理想熔体的物化性质及三元系的过剩物化性质关系如下:
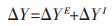
|
(12) |
式(12)中ΔYI为三元系理想熔体的物化性质,其表达式如下:
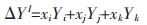
|
(13) |
In、Sn和Zn元素的相关物理化学参数如表 4所列。
| 表 4 In、Sn和Zn元素的相关物理化学参数 Table 4 Data of density and surface tension of pure metal |
 |
| 点击放大 |
根据文献所给的实验数据,分别利用原模型和改进模型对In-Sn-Zn三元系合金的表面张力,密度进行相应的计算,图 8~图 9为计算值与实验值的对比结果。
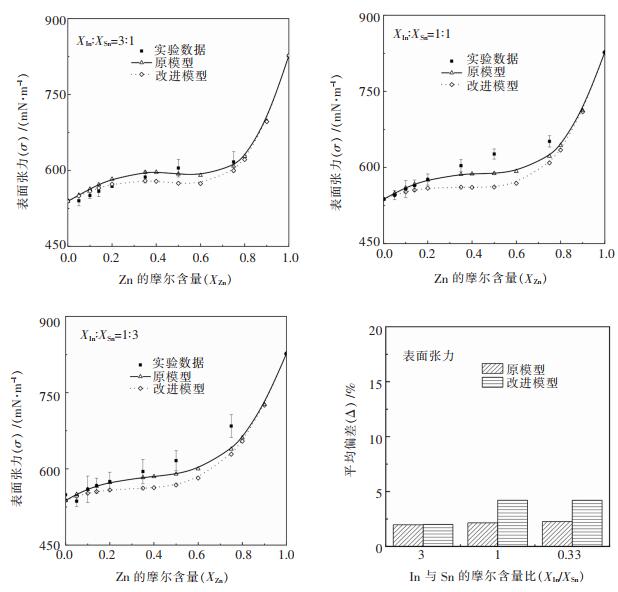 |
| 图 8 523 K下In-Sn-Zn体系表面张力计算值与参考文献值的比较结果 Fig. 8 Comparison of surface tension between theoretical models and literature data at 523 K for In-Sn-Zn alloys |
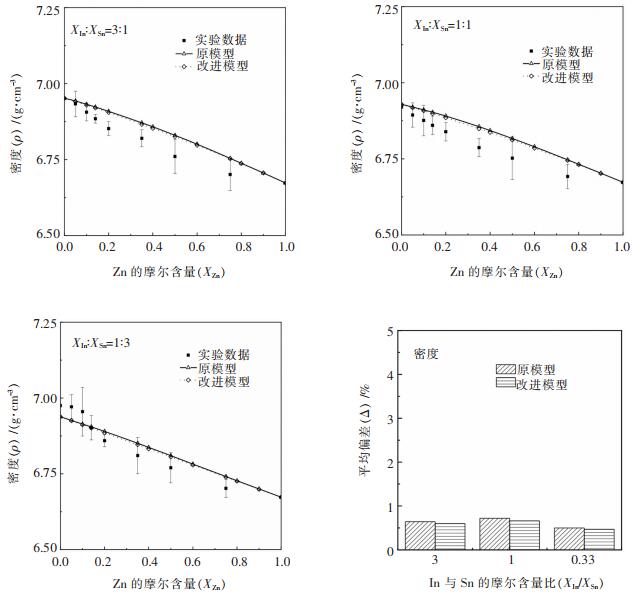 |
| 图 9 K下In-Sn-Zn体系密度计算值与参考文献值的比较结果 Fig. 9 Comparison of density between theoretical models and literature data at 523 K for In-Sn-Zn alloys |
通过观察图 8可以发现在所研究的温度范围下的截面,随着Zn含量的增加,In-Sn-Zn的表面张力也随之增加;综合来看,从富In截面到富Sn截面随着Sn含量的增加,In-Sn-Zn三元合金的表面张力也有小幅度提升,表明Sn元素在三元合金表面张力增加的过程中也起到一定的促进作用。根据对比结果来看,实验值和两预测曲线的变化趋势是一致的。随着Zn含量的增加,合金表面张力先小幅度地增大后急剧上升并无限接近纯金属Zn的表面张力值,两预测曲线的变化趋势也很好地体现出这一规律。原模型和改进模型对σIn-Sn-Zn的计算平均偏差都在2%~4%的范围内。
从In-Sn-Zn合金密度的对比结果来看,实验值和预测曲线的变化趋势是一致的,都是随着组元Zn的添加,合金密度逐渐下降,最后无限接近于纯金属Zn的密度,密度范围都在6~7 g/cm3, 原模型和改进模型对ρIn-Sn-Zn的计算平均偏差都在0.5%~0.7%的范围内。综合来看,改进前后模型的预测值相差不大,两预测曲线几乎重合。
2.2 Ag-Bi-Sn合金物化性质的预报Katayama等[28]采用电动势法系统地测试了Ag-Bi-Sn三元合金在900 K下Ag:Bi为1:3、1:1和3:1三个截面处组元Sn的活度以及偏摩尔超额吉布斯自由能,并根据式(6)达肯方程计算得到了Ag-Bi-Sn相应截面的全摩尔超额吉布斯自由能。Ag-Bi-Sn三元系合金的热力学参数如表 5所列。
| 表 5 Ag-Bi-Sn三元系合金液相热力学参数 Table 5 Thermodynamic parameters of Ag-Bi-Sn ternary alloy |
 |
| 点击放大 |
基于表 5中的热力学参数,运用原模型和改进模型,可获得Ag-Bi-Sn三元液态合金的过剩吉布斯自由能值。根据式(10)和式(11),可进一步获得组元Sn的局部热力学性质。
针对文献中报道的实验值进行点对点的计算,Ag-Bi-Sn三元系合金的全摩尔超额吉布斯自由能,组元Sn的偏摩尔超额吉布斯自由能以及活度的计算值与实验值的对比结果如图 10~图 12所示。
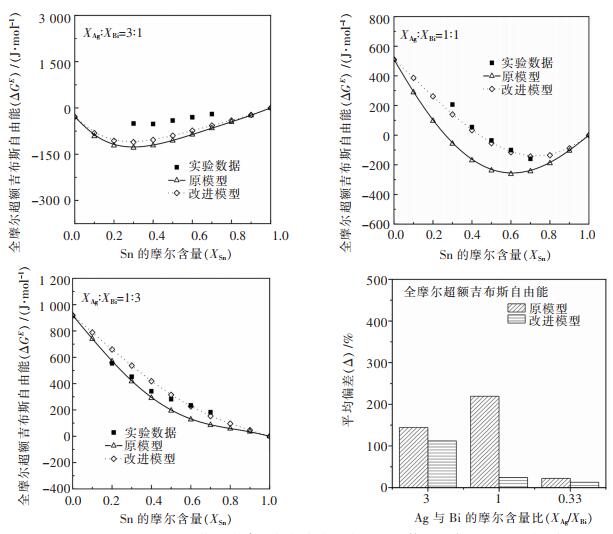 |
| 图 10 900 K下Ag-Bi-Sn体系全摩尔超额吉布斯自由能计算值与参考文献值的比较结果 Fig. 10 Comparison of integral molar excess Gibbs free energy between theoretical models and literature data at 900 K for Ag-Bi-Sn alloys |
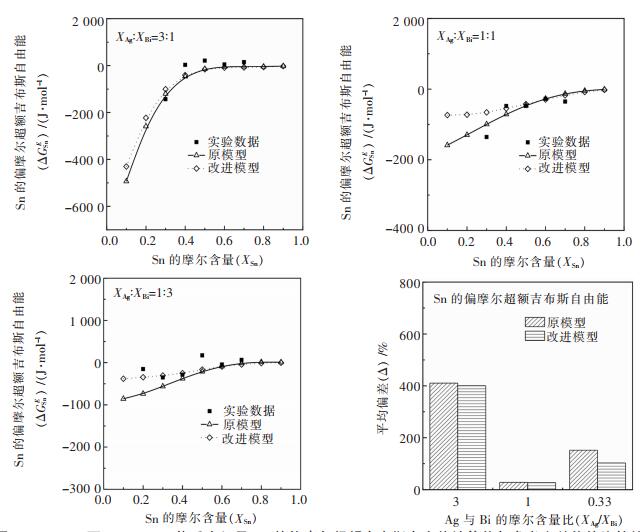 |
| 图 11 900 K下Ag-Bi-Sn体系中组元Sn的偏摩尔超额吉布斯自由能计算值与参考文献值的比较结果 Fig. 11 Comparison of partial molar excess Gibbs free energy of tin between theoretical models and literature data at 900 K for Ag-Bi-Sn alloys |
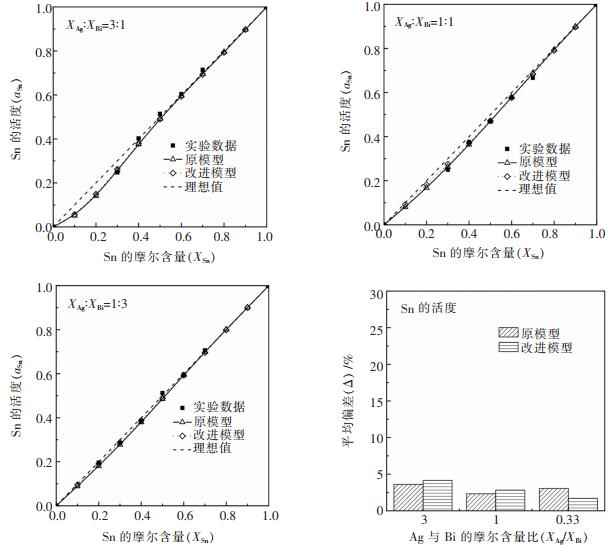 |
| 图 12 900 K下Ag-Bi-Sn体系中组元Sn的活度计算值与参考文献值的比较结果 Fig. 12 Comparison of activity of tin between theoretical models and literature data at 900 K for Ag-Bi-Sn alloys |
通过观察图 10可以发现在所研究的温度范围下,Ag:Bi为3:1时,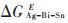
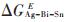
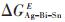
从Sn的偏摩尔超额吉布斯自由能的对比结果来看,实验值和预测曲线的变化趋势是一致的,在Ag:Bi为3:1截面处,实验点与两预测曲线拟合较好,Sn含量小于50%时,两预测曲线存在较小的偏差;在Ag:Bi为1:1和1:3截面处,Sn含量小于50%时,两预测曲线存在较明显的偏差,综合两截面处的对比结果来看,改进模型的预测曲线并没有什么问题,其问题可能是在Ag:Bi为1:1截面处Sn含量为30%所对应的实验值偏小。针对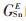
三元系合金中组元Sn的活度与浓度的关系似乎较为复杂,在Ag:Bi为3:1截面处,Sn含量较小时,aSn与理想值呈较小的负偏差,随Sn含量的增加,aSn逐渐靠近理想值;在Ag:Bi为1:1截面处,aSn与理想值均呈负偏差;在Ag:Bi为1:3截面处,aSn与理想值几乎重叠。就比较结果来看,两条预测曲线与实验点均拟合较好,且两条预测曲线几乎重合。
Hindler[32]采用座滴法系统地测定了Ag-Bi-Sn三元合金在873 K下Ag:Bi为1:2、1:1和2:1三个截面处的合金密度以及表面张力。3个二元系Ag-Bi,Bi-Sn和Sn-Ag的密度数据和表面张力数据取自文献[33-35],依旧采用R-K表达式拟合相应二元系的超额函数,Ag-Bi、Bi-Sn和Sn-Ag的超额表面张力函数和超额密度函数如表 6、表 7所列。图 13分别是R-K表达式对各二元系超额表面张力和超额密度的拟合结果。
| 表 6 873 K下Ag-Bi、Bi-Sn和Sn-Ag超额表面张力函数 Table 6 Excess surface tension of Ag-Bi, Bi-Sn and Sn-Ag binary alloy at 873 K |
 |
| 点击放大 |
| 表 7 873 K下Ag-Bi、Bi-Sn和Sn-Ag超额密度函数 Table 7 Excess density of Ag-Bi, Bi-Sn and Sn-Ag binary alloy at 873 K |
 |
| 点击放大 |
 |
| 图 13 R-K方程对Ag-Bi-Sn合金二元系超额表面张力和密度的拟合结果 Fig. 13 Fitting results of excess surface tension and density of Ag-Bi-Sn alloy binary system by R-K equation |
Ag、Bi和Sn元素的相关物理化学参数如表 8所列。
| 表 8 Ag、Bi和Sn的相关物理化学参数 Table 8 Data of density and surface tension of pure metal |
 |
| 点击放大 |
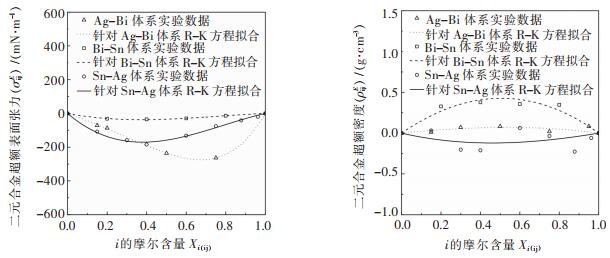
根据文献所给的实验数据,分别利用原模型和改进模型对Ag-Bi-Sn三元系合金的表面张力,密度进行相应的计算,图 14~图 15为计算值与实验值的对比结果。通过观察图 14可以发现在所研究的温度范围下的截面,随着Sn含量的增加,Ag-Bi-Sn的表面张力也随之增加;综合来看,从富Ag截面到富Bi截面随着Bi含量的增加,Ag-Bi-Sn三元合金的表面张力略有下降,而Ag元素对提高Ag-Bi-Sn三元合金的表面张力没有明显的影响。从对比结果来看,改进模型的预测曲线更靠近实验数据点,其平均偏差总体小于原模型。
 |
| 图 14 873 K下Ag-Bi-Sn体系表面张力计算值与参考文献值的比较结果 Fig. 14 Comparison of surface tension between theoretical models and literature data at 873 K for Ag-Bi-Sn alloys |
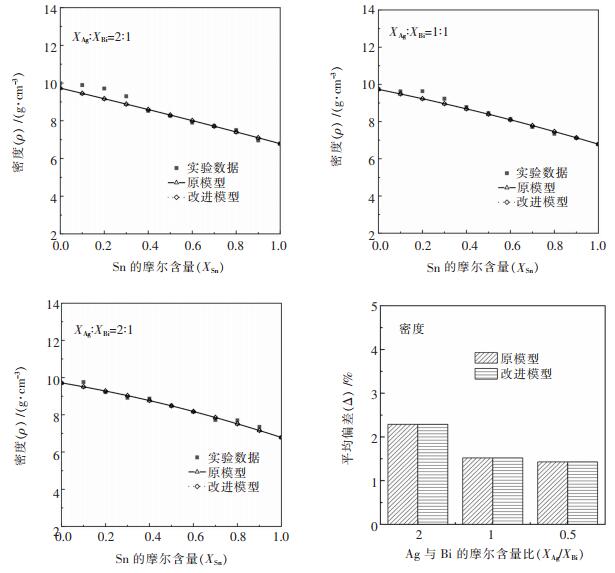 |
| 图 15 873K下Ag-Bi-Sn体系密度计算值与参考文献值的比较结果 Fig. 15 Comparison of density between theoretical models and literature data at 873K for Ag-Bi-Sn alloys |
从Ag-Bi-Sn合金密度的对比结果来看,实验值和预测曲线的变化趋势是一致的,都是随着组元Sn的添加,合金密度逐渐下降,最后无限接近于纯金属Sn的密度,密度范围都在6~10 g/cm3。改进前后模型的预测值相差不大,两预测曲线几乎重合,平均偏差均在1%~2%的范围内。
3 结论1)用正态分布函数表示二元系点性质对三元系点性质的“影响程度”,并将这一函数引入到新一代溶液几何模型当中以达到改进模型的目的。相较于原模型,改进模型打破了往常仅根据几个已知的二元系代表点的性质推测多元系性质的局限性,将二元系代表点邻近区间内所有点的性质和多元系点的性质联系在了一起。从“选点方式”的角度来看,与原模型相比,改进模型在理论上似乎更具有优势。
2)利用原模型和改进模型计算了In-Sn-Zn和Ag-Bi-Sn两个三元系的物化性质,并与实验结果进行了比较。综合来看,两个模型预报结果的平均偏差相差不大,单针对Ag-Bi-Sn体系热力学性质的预报方面,改进模型平均偏差相对较小些,这也进一步证明了考虑包括二元系代表点在内的邻近区间范围内所有二元系点性质这一改进思路的合理性。
| [1] |
董元篪, 王海川.
冶金物理化学[M]. 合肥: 合肥工业大学出版社, 2011: 31.
|
| [2] |
王常珍.
冶金物理化学研究方法[M]. 4版. 北京: 冶金工业出版社, 2013: 530.
|
| [3] |
杨振宁. 美与物理学[J].
武汉理工大学学报(信息与管理工程版), 2003, 25(1): 1–4.
DOI: 10.3963/j.issn.1007-144X.2003.01.001.
|
| [4] |
SCATCHARD G, TICKNOR L B, GOATES J R, et al. Heats of mixing in some non-electrolyte solutions[J].
Journal of the American Chemical Society, 1952, 74(15): 3721–3724. DOI: 10.1021/ja01135a002. |
| [5] |
HILLERT M. Empirical methods of predicting and representing thermodynamic properties of ternary solution phases[J].
Calphad, 1980, 4(1): 1–12. DOI: 10.1016/0364-5916(80)90016-4. |
| [6] |
KOHLER F. Estimation of the thermodynamic data for a ternary system from the corresponding binary systems[J].
Monatsh.Chem, 1960, 91(4): 738–740. DOI: 10.1007/BF00899814. |
| [7] |
MUGGIANU Y M, GAMBINO M, BROS J P. Enthalpies of formation of liquid alloys bismuth-gallium-tin at 723k-choice of an analytical representation of integral and partial thermodynamic functions of mixing for this ternary-system[J].
Journal de Chimie Physique et de Physico-Chimie Biologique, 1975, 72(1): 83–88. |
| [8] |
CHOU K C. A new solution model for predicting ternary thermodynamic properties[J].
Calphad, 1987, 11(3): 293–300. DOI: 10.1016/0364-5916(87)90048-4. |
| [9] |
TOOP G W. Predicting ternary activities using binary data[J].
Trans.TMS-AIME, 1965, 223: 850–855. |
| [10] |
周国治. 新一代的溶液几何模型及其今后的展望[J].
金属学报, 1997, 33(2): 126–132.
|
| [11] |
CHOU K C. A general solution model for predicting ternary thermodynamic properties[J].
Calphad, 1995, 19(3): 315–325. DOI: 10.1016/0364-5916(95)00029-E. |
| [12] |
CHOU K C, LI W C, LI F, et al. Formalism of new ternary model expressed in terms of binary regular-solution type parameters[J].
Calphad, 1996, 20(4): 395–406. DOI: 10.1016/S0364-5916(97)00002-3. |
| [13] |
BEHERA C K, SONAYE A. Measurement of zinc activity in the ternary In-Zn-Sn alloys by EMF method[J].
Thermochimica Acta, 2013, 568: 196–203. |
| [14] |
DARKEN L S. Application of the Gibbs-Duhem equation to ternary and multicomponent systems[J].
Journal of the American Chemical Society, 1950, 72(7): 2909–2914. DOI: 10.1021/ja01163a030. |
| [15] |
REDLICH O, KISTER A T. Algebraic representation of thermodynamic properties and the classification of solutions[J].
Industrial & Engineering Chemistry, 1948, 40(2): 345–348. |
| [16] |
李琴, 罗洋, 叶信宇, 等. 第一性原理计算在相图计算中的应用研究进展[J].
有色金属科学与工程, 2015, 6(6): 37–46.
|
| [17] |
ZIVKOVIC D, KATAYAMA I, YAMASHITA H, et al. Investigation of the thermodynamic model and ternary interaction parameter influence for Sn-Ag-Bi liquid alloys[J].
RMZ-Materials and Geoenvironment, 2006, 53(2): 155–161. |
| [18] |
LEE B J, OH C S, SHIM J H. Thermodynamic assessments of the Sn-In and Sn-Bi binary systems[J].
Journal of Electronic Materials, 1996, 25(6): 983–991. DOI: 10.1007/BF02666734. |
| [19] |
GANCARZ T, GASIOR W. EMF study of the liquid Sb-Sn-Zn Alloys[J].
Journal of Phase Equilibria and Diffusion, 2011, 32(5): 398. DOI: 10.1007/s11669-011-9916-8. |
| [20] |
LEE B J. Thermodynamic assessments of the Sn-Zn and In-Zn binary systems[J].
Calphad, 1996, 20(4): 471–480. DOI: 10.1016/S0364-5916(97)00009-6. |
| [21] |
CUI Y, LIU X J, OHNUMA I, et al. Thermodynamic calculation of the In-Sn-Zn ternary system[J].
Journal of Alloys and Compounds, 2001, 320(2): 234–241. DOI: 10.1016/S0925-8388(00)01484-5. |
| [22] |
PSTRUS J. Surface tension and density of liquid In-Sn-Zn alloys[J].
Applied Surface Science, 2013, 265: 50–59. DOI: 10.1016/j.apsusc.2012.10.098. |
| [23] |
赵飞, 陈志远, 陈洪智, 等. 1090 K下MgCl2-KCl-CaCl2三元熔盐体系的密度预测[J].
有色金属科学与工程, 2014, 5(4): 44–48.
|
| [24] |
严丽君, 王伟, 曹战民, 等. Ni3S2-FeS-Cu2S冰镍体系的表面张力[J].
稀有金属, 2000, 24(3): 161–166.
|
| [25] |
MOSER Z, GASIOR W, PSTRUS J, et al. Thermophysical properties of liquid In-Sn alloys[J].
International Journal of Thermophysics, 2009, 30(6): 1811. DOI: 10.1007/s10765-009-0663-6. |
| [26] |
PSTRUS J, MOSER Z, GASIOR W, et al. Surface tension and density measurements of liquid Sn-Zn alloys. experiment vs. SURDAT database of Pb-free solders[J].
Archives of Metallurgy and Materials, 2006, 51(3): 335–343. |
| [27] |
PSTRUS J, MOSER Z, GASIOR W. Surface properties of liquid In-Zn alloys[J].
Applied Surface Science, 2011, 257(9): 3867–3871. DOI: 10.1016/j.apsusc.2010.11.076. |
| [28] |
KATAYAMA I, TANAKA T, AKAI S, et al. Activity measurement of liquid Sn-Ag-Bi alloys by fused salt EMF method[J].
Materials Science Forum. Trans Tech Publications, 2005, 502: 129–138. DOI: 10.4028/www.scientific.net/MSF.502.129. |
| [29] |
KATTNER R U, BOETTINGER W J. On the Sn-Bi-Ag ternary phase diagram[J].
Journal of Electronic Materials, 1994, 23(7): 603–610. DOI: 10.1007/BF02653345. |
| [30] |
OHTANI H, SATOH I, MIYASHITA M, et al. Thermodynamic analysis of the Sn-Ag-Bi ternary phase diagram[J].
Materials Transactions, 2001, 42(5): 722–731. DOI: 10.2320/matertrans.42.722. |
| [31] |
ZIVKOVIC D, KATAYAMA I, MANASIJEVIC D, et al. Thermodynamics and phase diagram calculation of some sections in the Ag-Bi-Sn system[J].
Journal of the Serbian Chemical Society, 2007, 72(8/9): 901–909. |
| [32] |
HINDLER M, GUO Z, MIKULA A, et al. An investigation of the density and the surface tension in liquid Ag-Bi-Sn alloys[J].
Monatshefte für Chemie-Chemical Monthly, 2012, 143(9): 1243–1248. DOI: 10.1007/s00706-012-0773-x. |
| [33] |
GASIOR W, PSTRUS J, MOSER Z, et al. Surface tension and thermodynamic properties of liquid Ag-Bi solutions[J].
Journal of Phase Equilibria, 2003, 24(1): 40–49. DOI: 10.1007/s11669-003-0005-5. |
| [34] |
MOSER Z, GASIOR W, PSTRUS J. Surface tension measurements of the Bi-Sn and Sn-Bi-Ag liquid alloys[J].
Journal of Electronic Materials, 2001, 30(9): 1104–1111. |
| [35] |
MOSER Z, GASIOR W, PSTRUS J. Surface tension of liquid Ag-Sn alloys: experiment versus modeling[J].
Journal of Phase Equilibria, 2001, 22(3): 254. DOI: 10.1361/105497101770338734. |
 2020, Vol. 11
2020, Vol. 11


