上引连铸TU1热变形行为研究

引用本文

李鹏飞, 邓持清, 林新博, 齐亮, 姚幼甫, 徐高磊. 上引连铸TU1热变形行为研究[J]. 有色金属科学与工程, 2019, 10(3): 69-74. DOI: 10.13264/j.cnki.ysjskx.2019.03.012.

LI Pengfei, DENG Chiqing, LIN Xinbo, QI Liang, YAO Youfu, XU Gaolei. Research on the hot deformation of upward continuous casting TU1[J]. Nonferrous Metals Science and Engineering, 2019, 10(3): 69-74.DOI: 10.13264/j.cnki.ysjskx.2019.03.012.

上引连铸TU1热变形行为研究

[PDF全文]

李鹏飞¹ , 邓持清¹ , 林新博¹ , 齐亮¹ , 姚幼甫² , 徐高磊²

1. 江西理工大学材料科学与工程学院，江西赣州 341000;
2. 绍兴力博集团，浙江绍兴 312000

基金项目：江西省教育厅科技项目(GJJ180439)

通信作者：齐亮（1980-），男，博士，副教授，主要从事高性能金属材料组织性能控制与耐磨材料制备技术等方向，E-mail:ql0455@163.com

收稿日期：2018-12-25

摘要：以上引连铸TU1杆料为研究对象，在MMS-100热模拟试验机上对其进行单道次压缩试验，研究了在不同应变速率（0.01~10 s^-1）和不同变形温度（750~950 ℃）条件下的热变形行为，构建其本构模型.结果表明：在10 s^-1高应变速率条件下，TU1在750 ℃变形时峰值应力高达80 MPa，当温度升高到950 ℃时，峰值应力降至38 MPa；而在应变速率为0.01 s^-1、750 ℃变形时，峰值应力仅为30 MPa，此时TU1已经发生动态再结晶；通过本构方程计算得到TU1的热变形激活能约为253 kJ/mol.

关键词：TU1 热变形本构方程

Research on the hot deformation of upward continuous casting TU1

LI Pengfei¹ , DENG Chiqing¹ , LIN Xinbo¹ , QI Liang¹ , YAO Youfu² , XU Gaolei²

1. School of Material Science and Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China;
2. Shaoxing Libo Group, Shaoxing 312000, China

Abstract: The MMS-100 thermal simulation tester was utilized to perform a single pass compression test on the TU1 at different strain rates (0.01~10 s^-1) and different deformation temperatures (750~950 ℃). And its thermal deformation was studied to construct the constitutive equation. The experimental results show that the peak stress is 80 MPa at 750 ℃, 10 s^-1. When the deformation temperature increases to 950 ℃, the peak stress decreases to 38 MPa. But the peak stress is only 30 MPa at 750 ℃, 0.01 s^-1, and TU1 has undergone dynamic recrystallization. According to the constitutive equation, the thermal deformation activation of TU1 is about 253 kJ/mol.

Keywords: TU1 thermal deformation constitutive equation

上引连铸-CONFORM连续挤压工艺因其短流程、高效率被广泛的使用，目前在铜及铜合金接触线、优质铜扁线、异型材等产品已完成工业化生产^[1].采用连续挤压工艺对杆坯晶粒组织进行挤压处理，得到晶粒更为细小、均匀的细晶组织，实现细晶强化，从而大幅提高了材料的力学性能和使用安全性^[2].目前，王军等^[3]研究了纯铜在连续挤压过程中的组织演变及性能特征，阐明了纯铜在6个变形区的动态再结晶过程; 隋贤等^[4]对铜合金进行了深入探讨，解释了连续挤压中动态再结晶对铜合金细晶强化的过程，但针对连续挤压过程中力与微观组织演变相对不足.文中以上引TU1为研究对象，通过单道次热压缩实验，构建其本构方程，并分析了工艺参数如变形温度和应变速率分别对峰值应力和内部组织的影响规律，为连续挤压铜及铜合金的生产提供参考依据.

1 实验材料及方法

实验材料成分如表 1所列，试样为ϕ24 mm上引连铸杆经机加工制成ϕ10 mm×15 mm圆柱样.在MMS-100热模拟试验机进行单道次压缩实验，应变速率为0.01 s^-1，0.1 s^-1，1 s^-1，10 s^-1，变形温度为750 ℃，800 ℃, 850 ℃, 900 ℃，950 ℃，变形量为9 mm.一组20个试样分别在不同应变速率或不同变形温度下进行单道次压缩实验，对3组试样进行实验以保证结果的可重复性和准确性.

表 1 无氧铜TU1的化学成分/（质量分数，%） Table 1 The composition of TU1/(massfraction, %)

点击放大

2 实验结果与讨论 2.1 真应力-真应变曲线

图 1所示为TU1单道次热压缩变形的真应力应变曲线.由图 1可知，在相同应变速率下变形温度升高时，材料的峰值应力和流变应力都降低，这是由于温度的升高使原子扩散激活能增大，位错运动加剧，造成材料软化.在高应变速率1 s^-1下，由于压缩变形造成的加工硬化与动态再结晶造成的软化效果达到了动态平衡，所有变形温度对应曲线保持水平状稳定阶段；而在低应变速率0.01 s^-1，变形温度950 ℃时，对应的稳态阶段的曲线呈波浪形变化，这是由于低的应变速率下，变形缓慢，位错密度比高应变速率时增加少，造成形变储能较少与再结晶驱动力较小，动态再结晶与加工硬化的交替进行使得曲线呈波浪式^[5].

图 1 TU1不同变形温度下的真应力-真应变曲线 Fig. 1 The true stress-true strain curves of TU1 in different temperatures

图 2所示为=0.1 s^-1时拟合后的真应力-真应变曲线，图 3所示为应变硬化率-变形应力曲线，由图 2可知应变硬化率作为应变硬化模量会随着热变形过程的进行而逐渐减小，当材料开始有动态再结晶过程的发生时应变硬化率达到最小值，其在曲线上表现为的拐点即为临界应力，当θ=0时，其对应的值为峰值应力^[6].

图 2 拟合后的真应力-真应变曲线 Fig. 2 True stress-true strain curve of after fitting

图 3 应变硬化率-变形应力曲线 Fig. 3 Strain hardening rate-stress curve

图 4所示为变形温度与应变速率对峰值应力的影响.由图 4可知在应变速率一定时, TU1的峰值应力随温度升高而降低; 当变形温度一定时, 峰值应力随应变速率增大而升高.这是因为随着应变速率的增大, 变形过程中单位时间内增殖的位错密度增多, 使得位错的运动受阻.同时位错反应和攀移滑移等引起的软化现象相对较少, 材料的变形临界切应力也会增大, 导致峰值应力上升.此外由于变形时间缩短使得单位时间内动态再结晶的比例减少, 样品的软化减缓, 同样造成材料的峰值应力增大^[7].

图 4 变形温度与应变速率对流变应力峰值的影响 Fig. 4 Effects of deformation temperature and strain rate on peak stress

2.2 组织分析

为进一步研究热变形过程中力的变化原因，对变形后材料的微观组织进行分析. 图 5所示为变形温度为900 ℃，变形速率为0.01 s^-1、0.1 s^-1、1 s^-1、10 s^-1时试样的显微组织.由图 5中可知，TU1在变形温度为750 ℃，应变速率为0.01 s^-1时就已经发生了动态再结晶过程，同时随着温度升高晶粒会更加粗大，这是由于当温度高于材料的再结晶温度时，温度再升高会导致材料的过热度与晶粒长大的驱动力增大，同时较慢的变形速度使得新的晶粒有充足的时间进行长大，使得晶粒更加粗大，同时导致峰值应力下降，与前文所述结论一致^[8].

图 5 TU1在900 ℃下不同应变速率的显微组织 Fig. 5 Microstructures at 900 ℃ and different strain rates

图 6所示为应变速率为=0.01 s^-1，变形温度为750 ℃、800 ℃、850 ℃、900 ℃、950 ℃时试样的显微组织.由图 6可知，应变速率越大，晶粒表现为更加细小，这是由于变形速率增大时变形时间变短，使得晶粒没有足够的时间长大.同时，晶粒越细小材料的强度和硬度就会越大，在真应力-真应变曲线上表现为流变应力越大，符合前述结果^[9].

图 6 在

=0.01 s^-1下不同温度的显微组织 Fig. 6 Microstructures at

=0.01 s^-1 and different temperatures

2.3 构建本构方程

材料的热变形高温变形的本构关系可以通过2种典型的方程进行描述，一种是指数方程, 可以用于描述低应力水平:

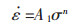
(1)

另一种适用于高应力水平:

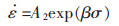
(2)

Tegart和Sellars等^[10-11]根据固体力学曾提出了一种结合变形激活能Q和变形温度的双曲正弦函数的流变应力与应变模型，其应变速率如式（3）所示:

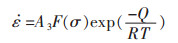
(3)

引入Zener-Hollomon公式后^[12]：

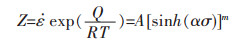
(4)

因此, 上述流变应力可以用式（5）表示为σ的函数^[13].

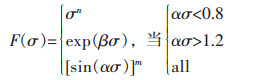
(5)

式（1）、式（2）、式（3）、式（4）、式（5）中, A₁, A₂, A₃, A, n, m均是材料的常数, Q是合金热压缩变形的激活能, R是气体常数（R=8.314）; , ασ和T分别是应变速率、流变应力和变形温度.

对式（1）和式（2）的等式进行适当的变形可得:

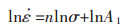
(6)

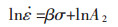
(7)

式（6）、式（7）中：n和β分别为ln-lnσ和ln-σ的斜率. 图 7所示为TU1不同温度下的流变应力峰值与应变速率的关系图.

图 7 ln

和lnσ的关系及ln

和σ的关系 Fig. 7 Relationship between ln

and lnσ, ln

and σ

由图 7可得：

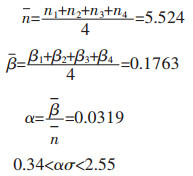
因此, 根据式（6）和式（7）可知, TU1的应变速率与流变应力大小和变形温度高低等的关系如式（8）所示：

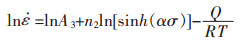
(8)

温度T一定时，对式（8）两边取偏导并整理得：

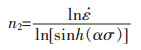
(9)

图 8所示为ln[sinh（ασ）]和的线性关系，绘制散点图并使用线性回归进行分析拟合，得到不同变形速率下n₂的值^[14].

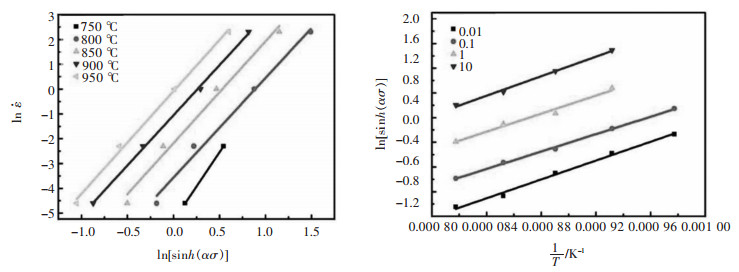图 8 ln

和ln[sinh（ασ）]的关系及ln[sinh（ασ）]和

的关系 Fig. 8 Relationship between ln

and ln[sinh(ασ)], ln[sinh(ασ)] and

由图 8可得：

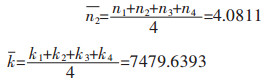
当变形速率一定时，对式（8）两边取偏导并整理得：

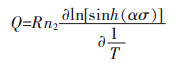
(10)

通过计算可得到再结晶激活能：

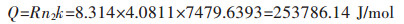
(11)

由式（1）、式（4）得：

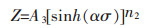
(12)

对式（8）、式（12）取对数得：

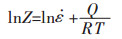
(13)

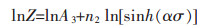
(14)

利用式（13）求出lnZ，图 9所示为lnZ与ln[sinh（ασ）]的线性关系图.由图 9可得拟合后的直线与y轴的截距即为lnA₃，且lnA₃=24.92, 则A₃=6.6672×10¹⁰；拟合的相关系数为0.992 0，拟合后直线斜率为4.088 9.

图 9 lnZ与ln[sinh（ασ）]的关系 Fig. 9 Relationship between lnZ and ln[sinh(ασ)]

综合国内外学者的研究成果^[15-19]可知，当金属材料的流变应力取决于变形温度和应变速率，同时峰值应力与稳态应力与此类似时，可以采用双曲正弦函数来描述材料的本构关系^[20]，故整理上述式子可得TU1的高温热变形单道次压缩行为的应力应变关系满足^[21]：

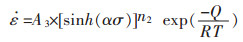
(15)

该方程可表示为:

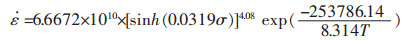
(16)

3 结论

1）在10 s^-1高应变速率条件下，TU1在750 ℃变形时峰值应力高达80 MPa，当温度升高到950 ℃时峰值应力降至38 MPa；而在应变速率为0.01 s^-1、750 ℃变形时峰值应力仅为30 MPa.

2）TU1在0.01 s^-1应变速率下，750 ℃时就已经有动态再结晶过程发生，且在相同应变速率时晶粒尺寸随着温度的升高而增大；在相同变形温度时晶粒尺寸随着应变速率的增加而减小.

3）TU1本构方程为：=6.6672×10¹⁰×，热变形激活能为253.786 kJ/mol.

参考文献

[1]	宋宝韫, 樊志新.连续挤压技术在我国的发展及应用[C]//2007全国有色金属加工装备技术创新大会论文集, 洛阳, 2007: 61-72. http://www.wanfangdata.com.cn/details/detail.do?_type=conference&id=6564259
[2]	袁远. 连续挤压对Cu-Cr-Zr合金接触线组织性能的影响[J]. 材料热处理学报, 2018, 39(2): 18–23.
[3]	王军, 运新兵, 李冰, 等. 纯铜连续挤压全过程的组织演变[J]. 有色金属(冶炼部分), 2011(5): 38–41. DOI: 10.3969/j.issn.1007-7545.2011.05.010.
[4]	隋贤, 宋宝韫, 李冰, 等. H65黄铜合金连续挤压过程中的组织和性能演变特征[J]. 中国有色金属学报, 2009, 19(6): 1049–1054. DOI: 10.3321/j.issn:1004-0609.2009.06.012.
[5]	刘庭光, 吴翔宇, 汪志刚, 等. 钇基稀土微合金化E36船板钢热模拟焊接探讨[J]. 有色金属科学与工程, 2017, 8(4): 42–46.
[6]	李银华, 刘平, 贾淑果, 等. 铜合金热变形行为研究[J]. 金属热处理, 2008, 33(8): 29–32.
[7]	程晨, 雷旻, 万明攀, 等. BT25钛合金高温变形行为[J]. 有色金属科学与工程, 2017, 8(6): 51–56.
[8]	郝齐齐, 曹延峰, 李智勇, 等. BFe10-1-1合金动态再结晶行为[J]. 塑性工程学报, 2018, 25(4): 206–211.
[9]	马吉苗, 刘峰, 刘龙明, 等. Cu-Ni-Si-P合金冷加工硬化及再结晶温度的研究[J]. 有色金属科学与工程, 2017, 8(2): 43–46.
[10]	李宁, 陈志宝, 刘建波. BFe10-1-1铜合金热力学行为[J]. 热加工工艺, 2017, 46(4): 114–116.
[11]	SELLARS C M, TEGART W J. On the mechanism of hot deformation[J]. Acta Metallurgica, 1966, 14(9): 1136–1138. DOI: 10.1016/0001-6160(66)90207-0.
[12]	ZENER C, HOLLOMON J H. Effect of strain rate upon plastic flow of steel[J]. J Appl Phys, 1944, 15(1): 22–32. DOI: 10.1063/1.1707363.
[13]	RAJAMUTHAMILSELVAN M, RAMANATHAN S. Hot deformation behaviour of 7075 alloys[J]. Journal of Alloys and Compounds, 2011, 509(3): 948–952. DOI: 10.1016/j.jallcom.2010.09.139.
[14]	刘欣, 李强锋, 汪志刚, 等. 低合金微碳钢的热变形行为及本构方程[J]. 有色金属科学与工程, 2018, 9(4): 53–59.
[15]	张晓菲, 彭成章, 肖阳, 等. 镍铝青铜高温变形的本构模型研究[J]. 热加工工艺, 2012, 41(20): 20–22.
[16]	ASHBY M F. A first report on deformation-mechanism maps[J]. Acta Metallurgica, 1972, 20(7): 887–897. DOI: 10.1016/0001-6160(72)90082-X.
[17]	应富强, 张更超, 潘孝勇. 金属塑性成形中的三维有限元模拟技术探讨[J]. 锻压技术, 2004, 29(2): 1–5. DOI: 10.3969/j.issn.1000-3940.2004.02.001.
[18]	余晖, KIM Y, 于化顺, 等. Mg-Zn-Zr-Ce合金高温变形行为与热加工性能研究[J]. 金属学报, 2012, 48(9): 1123–1131.
[19]	CHO M, KIM W B. A coupled finite element analysis of independently modeled substructures by pena penalty frame method[J]. KSME Int J, 2002, 16(10): 1201–1210. DOI: 10.1007/BF02983826.
[20]	何宇, 李学斌, 袁远. Cu-Mg合金连续挤压成形过程的数值模拟和试验对比分析[J]. 材料导报, 2017, 31(增刊1): 139–144.
[21]	孙军伟, 张荣伟, 李升燕, 等. 5182铝合金热变形行为研究[J]. 有色金属科学与工程, 2018, 9(5): 43–48.