| 基于分级分析法评价结构面对岩质高边坡稳定性的影响 |
2. 中国有色金属工业昆明勘察设计研究院有限公司,昆明 650000
2. Kunming Prospecting Design Institute of China Nonferrous Metals Industry, Kunming 650000, China
随着社会的进步与发展,出现了各种高度、形状不同的岩质边坡,加大了岩质边坡稳定性分析的难度.岩质边坡中存在各种各样的结构面,岩质边坡发生滑坡的一个重要因素就是结构面的存在.因此有必要在研究岩质边坡失稳破坏时,将结构面作为研究对象.传统方法往往是将岩质边坡内所有的结构面与整体边坡的坡面放在一起考虑,没有区分不同层次的结构面对整体边坡稳定性的影响程度,这将会使得本身规模很小的结构面,对整体边坡影响不大的结构面,误判称为主控结构面,使得分析结果和实际现场情况差距大[1-3].根据我国制定的《非煤露天矿边坡工程技术规范》(GB 51016-2014)[4]指出边坡稳定性计算方法、参数的确定,均需建立在边坡破坏模式分析的基础上,边坡的破坏模式是非常复杂的,需要综合考虑结构面、地下水、爆破等因素.传统的方法没有对结构面的规模与边坡的匹配性进行划分,因此需要研究岩体结构面规模与边坡规模层次匹配研究,这样才能准确的确定影响岩质边坡稳定性的主控结构面[5].因此,在对大型露天矿山岩质边坡稳定性评价时,应根据不同位置、不同规模结构面对矿山岩质边坡岩体稳定性的不同影响,进行矿山岩质边坡岩体工程稳定性分级分析,对边坡的稳定性问题做到整体和局部上的把握[6-10].
文中主要以大平掌铜矿东部边坡工程实例为研究对象,在综合搜集矿区勘探资料、地质剖面图、地形地质图、断裂构造图及地质报告等数据的基础上,现场进行结构面的详细调查,运用Midas-GTS建立整体三维模型进行大平掌铜矿东部边坡稳定性影响分析.
1 研究区工程概况大平掌采场东部边坡最高标高为1 380 m,最低标高为1 000 m,垂直高差达380 m.边坡上盘为破碎的英安岩,下盘为流纹岩,中间是松软的凝灰岩.断层发育较多,有2个较大的纵断层和许多小断层发育.东部岩石风化层较厚、风化程度较深,标高1 200 m以上岩石风化都比较强烈,导致岩石稳定性较差.工程区内主要分布有5条断层,分别为F1断层、F2断层、F3断层、F4断层和F5断层(见图 1).
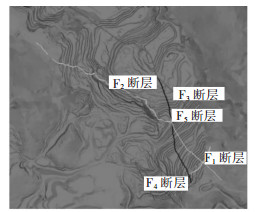 |
| 图 1 大平掌铜矿项目区地质构造 Fig. 1 Geological structure map of Dapingzhang copper mine project area |
2 研究区边坡岩体稳定性分级分析 2.1 边坡岩体结构基本特征
图 2所示为大平掌铜矿采场东部边坡全貌.总体边坡沿北东—南西方向延伸,边坡长1 150 m,边坡最高标高为1 380 m,最低标高为1 000 m,边坡高度380 m,宽度530 m,坡向326 °,坡角19 °.依据台阶边坡坡角参数的变化情况,总体边坡划分为3个组合台阶边坡,组合台阶边坡A:1 000~1 160 m台阶高度10 m,平台宽度10 m,台阶边坡坡角53°,开采帮坡角为13°;组合台阶边坡B:1 160~1 280 m台阶高度10 m,平台宽度8 m,台阶边坡坡角65°,开采帮坡角为29°;组合边坡C:1 280~1 380 m台阶高度10 m,平台宽度10 m,台阶边坡坡角57°,开采帮坡角为25°.
 |
| 图 2 东部边坡全貌 Fig. 2 Eastern slope |
边坡岩体自下往上依次出露流纹岩、凝灰岩和英安岩,其中英安岩发育新鲜未风化、微风化、中风化、强风化、全风化完整的风化剖面,边坡表层覆盖有土壤层.边坡范围发育5条断层,凝灰岩呈层状分布,构成边坡岩体软弱夹层,边坡范围内普遍发育3组节理,强风化英安岩还发育有一组风化节理,边坡岩体结构面发育特征列于表 1.(注:节理产状为统计平均值)
| 表 1 边坡岩体结构面发育特征 Table 1 Development characteristics of slope rock mass structure |
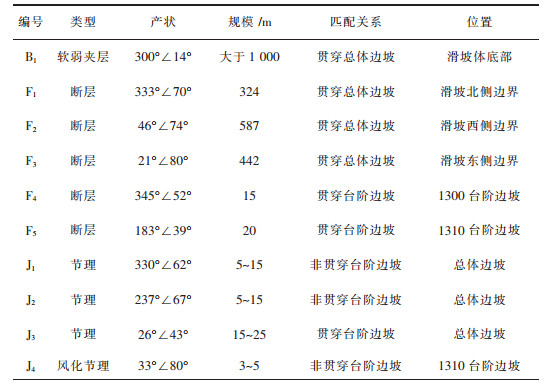 |
| 点击放大 |
图 3所示为按照传统分析方法绘制的边坡稳定性赤平投影,该方法将贯穿总体边坡的大规模断层(规模分别为324 m、587 m、442 m)、贯穿台阶边坡的小规模断层(规模分别为15 m、20 m)、节理(规模5~25 m)、风化节理(规模3~5 m)投影在同一个边坡上进行分析,忽略了结构面不同空间分布位置、不同规模对边坡整体稳定性的差异化影响,难以得到客观、全面的稳定性分析结论.因此,需要开展总体边坡整体稳定性的分级分析.
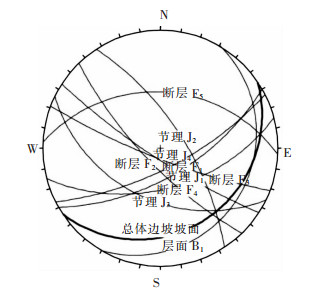 |
| 图 3 边坡岩体稳定性赤平投影分析 Fig. 3 Stereospheric projection analysis of slope rock mass stability |
2.2 总体边坡岩体稳定性分析
1)总体边坡整体稳定性分析:总体边坡发育有断层F1、断层F2、断层F3和层面B1等4条贯穿性结构面.由图 4可知,总体边坡坡向326°,坡角19°;层面B1产状300°∠14°,其倾向与边坡倾向交角为26°,倾向坡外,其倾角小于坡角;断层F1产状333°∠70°,其倾向与边坡倾向交角为7°,顺坡向,断层面倾角大于坡角.断层F1与层面B1形成的组合式潜在滑移面控制了总体边坡的整体稳定性.断层F2产状46°∠74°和断层F3产状21°∠80°,这两组基本垂直的贯穿性结构面可作为边坡潜在滑移破坏的割离边界.凝灰岩遇水物理力学性质发生劣化,可作为边坡岩体的软弱夹层,成为总体边坡发生整体破坏的主滑移面.
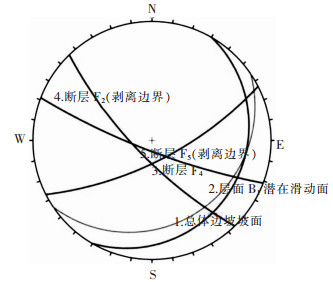 |
| 图 4 总体边坡整体稳定性赤平投影分析 Fig. 4 Stereoscopic projection analysis of overall slope stability |
2)总体边坡局部稳定性分析:节理和小规模断层,与层面、断层等贯穿性结构面共同控制总体边坡的局部稳定性.依据边坡不同部位的岩体结构面空间分布及其组合特点,按不同边坡部位分别进行总体边坡的局部稳定性分析,图 5所示为总体边坡局部稳定性的赤平投影分析结果.
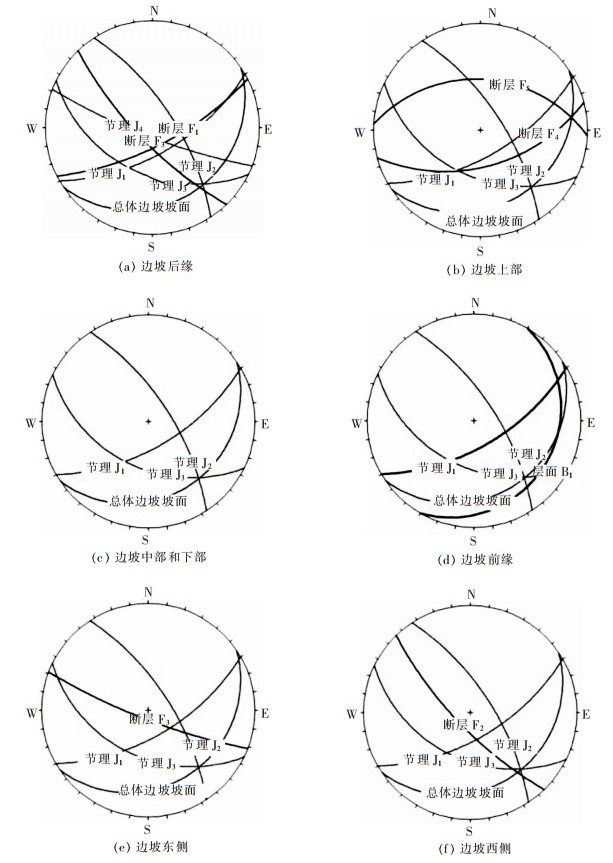 |
| 图 5 总体边坡局部稳定性赤平投影分析 Fig. 5 Analysis of the local stability of the overall slope |
结果显示边坡后缘、边坡上部、边坡中部和下部、边坡东侧及边坡西侧的局部稳定性好,总体边坡前缘的局部稳定性较差.
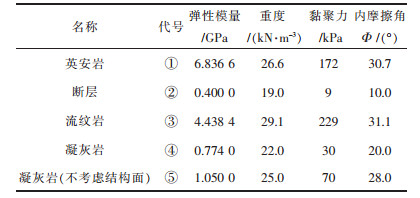
3 东部边坡三维模型建立及分析 3.1 三维有限元分析东部边坡模型的建立在通过大量的试算,确定了计算模型范围,见图 6.模型为长方体,其长、宽、高分别为407 m、254 m、330 m,体积34 114 740 m3,三维计算参数如表 2所示.
 |
| 图 6 建模范围平面 Fig. 6 Modeling range plan |
| 表 2 现状条件计算参数 Table 2 Current condition calculation parameter |
 |
| 点击放大 |
三维模型建立.根据勘察资料提供的剖面图,首先将A、B、C剖面导入到Midas-GTS中建立边坡实体模型,在通过Misdas-GTS中的地形生成器生成的地表曲面,删除地表地形上的实体,形成计算模型如图 7所示,不考虑结构面的计算模型如图 8所示.之后进行网格划分得到最终的计算模型如图 9所示.
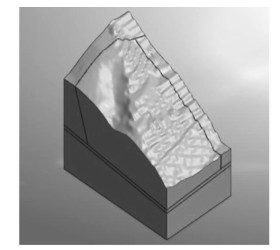 |
| 图 7 计算模型(考虑结构面) Fig. 7 Calculation model (considering structural plane) |
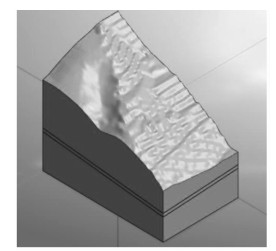 |
| 图 8 计算模型(不考虑结构面) Fig. 8 Calculation model (regardless of structural plane) |
 |
| 图 9 不同加高条件下模型网格划分 Fig. 9 Model meshing under different elevation conditions |
3.2 东部边坡稳定性分析 3.2.1 考虑结构面条件下稳定性分析
图 10所示为考虑结构面条件下位移、应力、应变图的三维数值模拟结果.
 |
| 图 10 考虑结构面条件下位移、应力、应变 Fig. 10 Consider displacement, stress and strain diagram under structural plane conditions |
3.2.2 不考虑结构面条件下稳定性分析
图 11所示为不考虑结构面条件下位移、应力、应变图的三维数值模拟结果.
 |
| 图 11 不考虑结构面条件下的位移、应力、应变 Fig. 11 Displacement, stress, strain diagram without considering structural plane conditions |
通过图 10和图 11可知,不考虑结构面对东部边坡的影响时,东部边坡的整体安全系数为1.651 6,而考虑结构面对东部边坡的影响时,东部边坡的整体安全系数为1.212 9,相比较下安全系数下降了26.5 %,并且根据规范规定,当考虑结构面的影响时,东部边坡的整体状态处于极限平衡状态,如果考虑到降雨和爆破对东部边坡的影响,东部边坡很可能发生破坏[11-13].
通过图 10(A)、图 10(B)和图 11(A)、图 11(B)可知,东部边坡的整体位移都集中在坡角处,但是当考虑结构面的影响时,总体位移集中在断层F2附近,而不考虑结构面时,总体位移符合正常的滑坡状态,主要集中在滑体上,说明结构面影响了东部边坡的整体位移趋势,从滑体中部转移到了结构面上.
通过图 10(C)~图 10(E)、图 10(c)~图 10(e)和图 11(C)~图 11(E)、图 11(c)~图 11(e)可知,在仅考虑自重的情况下,东部边坡的总体应力均是从上往下逐渐增大;考虑结构面时,从云图可知东部边坡的最大剪应变集中在断层F1、断层F2并且主要趋势基本沿着凝灰岩层;而不考虑结构面对东部边坡的影响时,最大剪应变类似于圆弧状,主要集中在坡脚台阶边坡处,说明在不考虑结构面的影响时,东部边坡最容易发生破坏的地方在坡脚台阶边坡,而当考虑了结构面对东部边坡的影响时,最容易发生破坏的地方主要集中3个结构面处:断层F1、断层F2和凝灰岩层.
3.3 降雨条件下东部边坡稳定性分析根据现场的勘察可知,东部边坡在凝灰岩层以及1 100 m处有出水,可知地下水位线在凝灰岩层上部,定义边坡前部节点水头为1 105 m,边坡后部节点水头为1 155 m.大平掌东部边坡的日最大降雨量为145.1 mm,最长连续降雨62天,因此定义降雨后的边坡前部节点水头为1 115 m,边坡后部的节点水头为1 165 m.地下水和降雨工况下三维计算参数如表 3所列.
| 表 3 降雨条件计算参数 Table 3 Rainfall condition calculation parameter |
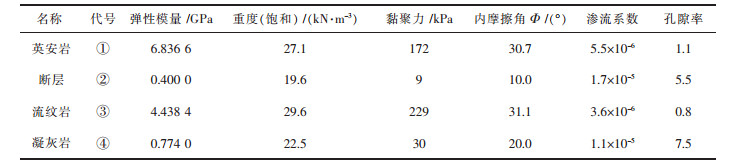 |
| 点击放大 |
3.3.1 正常水位条件下稳定性分析
图 12所示为正常水位下的孔隙水压力、位移、最大剪应变的三维数值模拟结果.
 |
| 图 12 正常水位下的孔隙水压力、位移、最大剪应变 Fig. 12 Pore water pressure, displacement and maximum shear strain at normal water level |
3.3.2 降雨条件下稳定性分析
图 13所示为降雨条件下的孔隙水压力、位移、最大剪应变的三维数值模拟结果.
 |
| 图 13 降雨条件计算参数 Fig. 13 Rainfall condition calculation parameter |
通过图 12和图 13可知,不考虑降雨对东部边坡的影响时,东部边坡的整体安全系数为1.071 7,而考虑降雨对东部边坡的影响时,东部边坡的整体安全系数为1.055 2,相对于只考虑地下水位线安全系数下降了1.53 %,并且根据规范规定,无论是否考虑降雨,东部边坡都很可能发生破坏变形.
通过图 12(A)、图 12(a)和图 13(A)、图 13(a)可知,东部边坡在考虑降雨的情况下,孔隙水压力较不考虑降雨的情况下增大,因此应该对降雨入渗所产生的不良影响给予足够重视.通过图 12(B)~图 12(C)、图 12(b)~图 12(c)和图 13(B)~图 13(C)、图 13(b)~图 13(c)可知,东部边坡的整体位移都集中在坡角处,但是考虑降雨较不考虑降雨位移增大1.5倍.通过图 12(D)、图 12(d)和图 13(D)、图 13(d)可知,当考虑降雨的影响时,最大剪应变是不考虑降雨时最大剪应变的5倍.
4 结论1)结构面对于东部边坡的Z向位移、总体方向的位移影响较大,考虑结构面相对于不考虑结构面的Z向位移增大了20 cm,总体方向位移增大了10~20 cm.说明结构面的存在使得边坡的破坏位移增大,危害性更大.
2)根据模型计算出来的安全系数来看,考虑结构面相对于不考虑结构面安全系数下降了26.5 %.根据最大剪应力图来看,考虑结构面时,东部边坡发生破坏是沿着结构面发生破坏,而不考虑结构面时,东部边坡较为稳定.说明结构面对东部边坡的安全系数以及破坏模式有很大的影响[14-19].
3)通过对比考虑降雨和不考虑降雨、地下水2种分析结果可知,安全系数下降了13 %并且接近1.0,这种情况极易发生滑坡.当考虑降雨时,最大剪应变的范围更接近断层F1和凝灰岩层,说明降雨使凝灰岩层软化,使断层F1的力学性能降低,更容易造成东部边坡沿断层F1和凝灰岩层下滑,尤其是沿凝灰岩层的下滑趋势更大,因此也说明了东部边坡的主控结构面是软弱结构面凝灰岩层.建议对东部边坡采用水平排水孔降水疏干,来防止降雨所导致的滑坡产生[20-24].
4)通过现场与实验分析对比可以知道,结构面对整体东部边坡的影响很大.从经济和效益的角度考虑,应该着重对整体东部边坡的结构面进行治理[25].
| [1] |
HE M C. Real-time remote monitoring and forecasting system for geological disasters of landslides and its engineering application[J].
Chinese Journal of Rock Mechanics and Engineering, 2009, 28(6): 1081–1090. |
| [2] |
YAN G J. Approach to the study & prevention-cure of mines geologic disasters[J].
China Mining Magazine, 2004, 13(3): 66–68. |
| [3] |
LI S L. Study on the geological hazard in metal mines and its prevention countermeasures[J].
The Chinese Journal of Geological Hazard and Control, 2002, 13(4): 44–48. |
| [4] |
GB 51016-2014, 非煤露天矿边坡工程技术规范[S].北京: 中国计划出版社, 2014.
|
| [5] |
GU F H. Failure types and damage scale analysis of bench slope based on geometrical characteristics[J].
Metal Mine, 2014, 43(7): 51–55. |
| [6] |
黄洪波.层状岩质边坡的稳定性分析[D].杭州: 浙江大学, 2003.
http://cdmd.cnki.com.cn/Article/CDMD-10335-2003041724.htm |
| [7] |
欧敏.滑坡演化过程CA预测理论研究及应用[D].重庆: 重庆大学, 2006.
http://cdmd.cnki.com.cn/Article/CDMD-10611-2006176227.htm |
| [8] |
段建.岩质边坡稳定性分析及其危险滑移路径搜索研究[D].长沙: 中南林学院, 2005.
http://cdmd.cnki.com.cn/Article/CDMD-10538-2005101226.htm |
| [9] |
江春明, 刘文连, 阿发友, 等. 大平掌露天矿岩质边坡稳定性有限元分析[J].
价值工程, 2016, 35(17): 194–197.
|
| [10] |
刘志清.基于蚁群算法的岩质边坡稳定性分析[D].北京: 中国地质大学(北京), 2008.
http://cdmd.cnki.com.cn/Article/CDMD-11415-2008068716.htm |
| [11] |
杨金林.不同形状边坡稳定性研究及其工程应用[D].长沙: 中南大学, 2011.
http://cdmd.cnki.com.cn/Article/CDMD-10533-1011181783.htm |
| [12] |
张昀青, 刘维宁, 赵逊. 岗南水库大坝安全稳定分析[J].
中国安全科学学报, 2003(4): 58–62.
|
| [13] |
张彬.岩质边坡半隧洞超前支护结构数值研究[D].西安: 西安理工大学, 2010.
http://cdmd.cnki.com.cn/Article/CDMD-10700-2010140788.htm |
| [14] |
叶季平.金湖泵站高边坡稳定性研究[D].武汉: 武汉大学, 2004.
http://cdmd.cnki.com.cn/Article/CDMD-10486-2004112670.htm |
| [15] |
任志丹.含软弱夹层边坡的稳定性分析[D].昆明: 昆明理工大学, 2015.
|
| [16] |
宫宇生. 岩质边坡稳定性影响因素分析及其加固措施研究[J].
科技与企业, 2015(14): 143–148.
DOI: 10.3969/j.issn.1004-9207.2015.14.137.
|
| [17] |
杜时贵, 程俊杰, 王思敬. 岩体的基本构成-结构面和结构体[J].
工程地质学报, 2000, 8(增刊1): 305–308.
|
| [18] |
杜时贵, 郭霄, 吕建伟. 岩体结构面抗剪强度估算方法研究进展[J].
金华职业技术学院学报, 2004(3): 1–5.
DOI: 10.3969/j.issn.1671-3699.2004.03.001.
|
| [19] |
周增意. 有关岩体结构面强度的讨论[J].
中国水运(理论版), 2007(7): 116–117.
|
| [20] |
王猛.金沙江乌东德水电站河门口坝址溢洪道边坡稳定性研究[D].成都: 成都理工大学, 2006.
http://cdmd.cnki.com.cn/Article/CDMD-10616-2006139613.htm |
| [21] |
罗强, 赵炼恒, 李亮, 等. 基于Barton-Bandis准则的锚固边坡稳定性分析[J].
岩土力学, 2013, 34(5): 1351–1359.
|
| [22] |
余明.边坡稳定性分析方法在昭永公路上的应用[D].重庆: 重庆交通大学, 2015.
http://cdmd.cnki.com.cn/Article/CDMD-10618-1016158817.htm |
| [23] |
宋享桦, 刘俊岩, 刘燕.基于临界稳定的某石灰岩质基坑软弱结构面参数反分析[A]//中国土木工程学会.中国土木工程学会2016年学术年会论文集[C].北京: 中国土木工程学会, 2016: 13.
|
| [24] |
李曙锋;贺跃光. 露天矿山边坡变形监测及工程实例[J].
有色金属科学与工程, 2002, 3(2): 1–4.
|
| [25] |
余清仔. 德兴铜矿露采矿区岩体结构特征对边坡稳定性的影响[J].
江西有色金属, 1992, 5(2): 102–106.
|
 2019, Vol. 10
2019, Vol. 10


