| 基于未确知测度模型的稀土原地浸矿地下水污染风险评价 |
b. 江西理工大学应用科学学院,江西 赣州 341000;
c. 江西理工大学外语外贸学院,江西 赣州 341000
b. College of Applied Sciences, Jiangxi University of Science and Technology, Ganzhou 341000, China;
c. Faculty of Foreign Studies, Jiangxi University of Science and Technology, Ganzhou 341000, China
离子型稀土矿开采经历了从池浸、堆浸到原地浸矿工艺的转变. 2004年之后,离子型稀土原地浸矿新工艺被推广使用,该工艺是在稀土矿体区域布置注液井网,向注液井内注入硫酸铵溶浸液,溶浸液向矿体渗透过程中与稀土离子发生交换反应形成稀土母液,通过集液沟收集母液至集液池,用草酸沉淀母液中的稀土,实现资源回收的目的.由于原地浸矿过程中不需剥离植被及表土,不开挖搬运矿体,不存在难处理的尾渣,被称为绿色高效开采工艺.但该工艺实施过程中,需要向矿体注入大量硫酸铵浸矿液,据统计,每获取1 t氧化物稀土,需要注入7~8 t硫酸铵,若浸出液一旦污染地下水,后果不堪设想[1-4].根据多年的稀土矿山生产调查,花岗岩、次花岗斑岩和凝灰岩形成的风化壳离子吸附型稀土矿床在不存在大的断裂导水带时,一般集液率在90 %以上,例如广东省大埔县五丰稀土矿集液率为92.35 %[5],广东省平远县仁居稀土矿集液率为93.92 %[6-7],但仍不可避免有部分浸矿液不能有组织地收集、渗漏或部分由土壤和植物吸收、蒸发.对底板存在大的断裂导水带的离子型稀土矿,浸出母液将会沿底板裂隙渗漏,使收液率明显降低,不仅浪费了稀土资源,更严重的是污染了水资源.目前,渗漏已成为离子型稀土原地浸矿工艺推广应用中面临的“瓶颈”问题,对离子型稀土原地浸矿地下水污染进行风险评价具有重要的意义.
为使评价结果更加符合实际情况,需要采用适当的方法处理这些未确知信息.未确知数学理论[8]是有别于灰色理论和模糊数学的一种新的不确定性方法.彭康等[9], 董陇军等[10], 栾婷婷等[11]分别将未确知测度评价模型应用于尾矿库溃坝风险、边坡地震稳定性综合评价以及排土场滑坡风险评价,取得了合理的结果.本研究将应用未确知测度的模型,通过信息熵理论确定影响因素的权重,对原地浸矿前、浸矿中、浸矿后以及私采矿区地下水污染情况进行风险评价,以寻求地下水污染评价方法的突破.
1 构建未确知测度评价模型的地下水污染风险评价指标体系 1.1 未确知测度模型的基本原理设某评价对象R有n个,那么评价对象空间为R={R1,R2,…,Rn},而每个评价对象Ri(i=1,2,…,n)又都有m个评价因素,那么它的评价空间为X={X1,X2,…,Xm},则Ri可表示成m维向量Ri={xi1,xi2,…,xim},这里面xij所表示的就是研究对象Ri关于评价指标Xj的测量值.对每个子项xij(i=1,2,…,n;j=1,2,…,m),设有P个评价等级(C1,C2,…,Cp),评价空间记为U,U={C1,C2,…,Cp}.设C1 < C2 < C3 < … < Cp或C1 > C2 > C3 > … > Cp,我们就称{C1,C2,…,Cp}是评价空间U的一个有序分割类[10].由于每一个指标的分类标准都是知道的,所以可以将分类标准矩阵写为:

|
(1) |
式(1)中,aijk表示评价指标Xj的等级为Cp的评价标准值,满足aij1 < aij2 < … < aijp.
1)构造单指标未确知测度aij1 < aij2 < … < aijp.若μijk=μ(xij∈Ck)表示的是测量值xij属于第K个评价等级Ck的程度,μ则要符合以下条件:
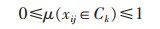
|
(2) |
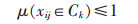
|
(3) |
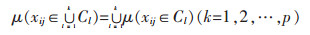
|
(4) |
满足式(2)~式(4)的μ被称为未确知测度,简便称作测度,式(2)被称作测度的非负有界性,式(3)称为μ对评价空间U满足“归一性”,式(4)称作μ对评价空间U的“可加性”,若μ满足不了归一性与可加性,就可以判断μ的值理论上便是不可信的.在测度μ前加上“未确知”的理由是决策者通常是在信息不完全的情况下构造的测度函数,所以除了必须的先验知识,还含有决策者个人的主观因素,包括偏好、需求等.
从给出的未确知测度定义出发,构造单指标测度函数:
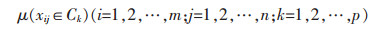
|
(5) |
式(5)有助于计算出评价因素的各个指标测度值μijk,则称矩阵(μijk)m×p为单指标测度评价矩阵.
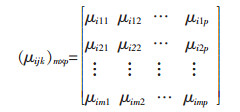
|
(6) |
设aij1 < aij2 < … < aijp,有
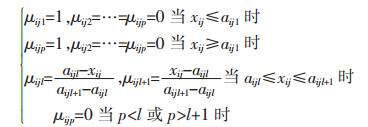
|
(7) |
2)确定各指标权重.令wj为Xj的权重,wj表示为测量指标xij与其他指标相比较之后所具有的相对重要程度,0≤wj≤1,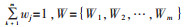
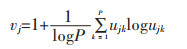
|
(8) |
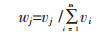
|
(9) |
其中,ujk表示单指标测度评价矩阵,为已知数,所以可以依据式(8)和式(9)计算得到各指标的权重wj.
3)计算多指标综合未确知测度.若μik=μ(R∈Ck),评价样本Ri归属于第K个评价类Ck等级的程度,则有
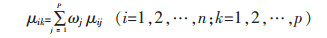
|
(10) |
显然有0≤μik≤1以及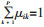
4)样本判定.如果C1 < C2 < C3 < … < Cp或者C1 > C2 > C3 > … > Cp,那么称{C1 > C2 > C3 > … > Cp}为评价空间U的一个有序分割类.可引入“置信度”评价准则如下:设λ为置信度(1≥λ > 0.5),通常取λ=0.6或0.7,且令
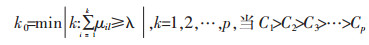
|
(11) |
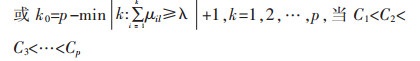
|
(12) |
则认为评价样本Ri归属于第k0个评价等级Ck0.该准则是从“强”的角度出发的,也就是认为越“强”就越好,并且“强”的类应该占据相当大的比例.
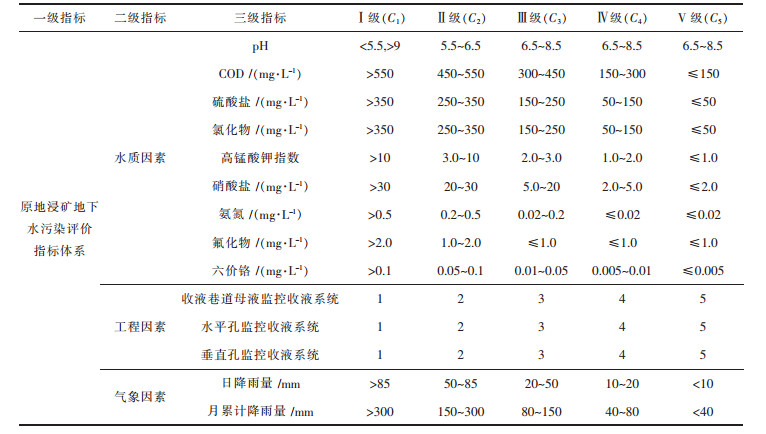
1.2 地下水污染风险评价指标体系的建立影响离子型稀土矿地下水污染的因素很多,本研究选择典型稀土矿山为样本,在借鉴相关文献研究成果[12-16]的基础上,建立原地浸矿地下水三级评价指标体系,如表 1所列.该评价指标体系包含水质因素、工程措施因素、气象因素这3个二级指标,以及水质监测指标pH值I1、溶解性固体(COD)I2、硫酸盐I3、氯化物I4、高锰酸钾指数I5、硝酸盐I6、氨氮I7、氟化物I8、六价铬I9、收液巷道母液监控收液系统I10、水平孔监控收液系统I11、垂直孔监控收液系统I12、气象系统日降雨量I13和月累计雨量I14共14个三级指标.每个三级指标分为5个评价等级,Ⅰ级、Ⅱ级、Ⅲ级、Ⅳ级和Ⅴ级分别对应于{C1 > C2 > C3 > C4 > C5},表示发生水质污染的危险性极高、危险性较高、危险性一般、危险性较低和无污染.对于3个定性指标,先根据指标的分级标准,进行定性到定量的转化,见表 1和表 2所列.
| 表 1 原地浸矿地下水污染评价指标体系及对应的评价等级 Table 1 Index system of groundwater pollution in situ leaching and corresponding classification criterion |
 |
| 点击放大 |
| 表 2 原地浸矿地下水污染评价定性指标 Table 2 Classification criterion of qualitative indexes in the evaluation of groundwater pollution in situ leaching |
 |
| 点击放大 |
每级都有一个规定的数值区间,根据前面单指标测度函数的定义和表 1中各评价指标的赋值标准,构建稀土矿原地浸矿地下水污染风险评价指标体系的各指标测度函数,选择直线型测度函数,如式(13)所示.
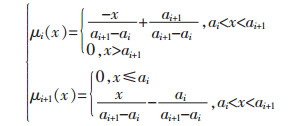
|
(13) |
其中,ai是对象属性观测值分布区间上的点,假设在点ai的左侧的属性值处于状态,当属性值从ai增加到ai+1的过程中,属性i的状态的程度逐渐减弱,至ai+1时,i状态的程度减为0,与此同时,当观测值ai从增加到ai+1时,属性观测值的i+1状态程度由0增加到1,则11个定量评价指标的单指标测度函数依次如图 1~图 11所示.
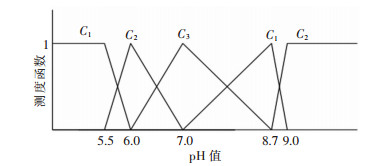 |
| 图 1 pH的单指标测度函数 Fig. 1 Uncertainly measurement function of pH |
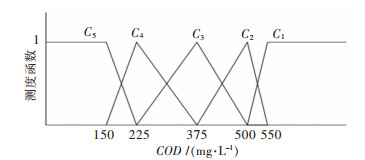 |
| 图 2 COD的单指标测度函数 Fig. 2 Uncertainly measurement function of COD |
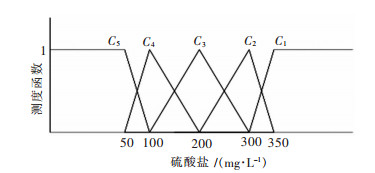 |
| 图 3 硫酸盐的单指标测度函数 Fig. 3 Uncertainly measurement function of sulfate |
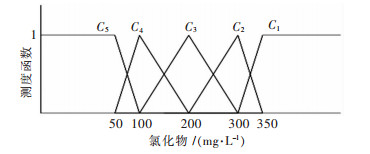 |
| 图 4 氯化物的单指标测度函数 Fig. 4 Uncertainly measurement function of chloride |
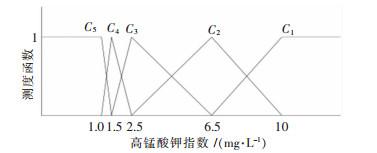 |
| 图 5 高锰酸钾指数的单指标测度函数 Fig. 5 Uncertainly measurement function of Potassium permanganate index |
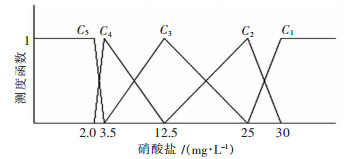 |
| 图 6 硝酸盐的单指标测度函数 Fig. 6 Uncertainly measurement function of nitrate |
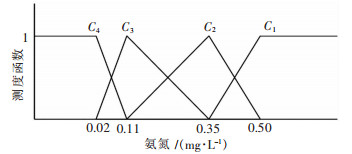 |
| 图 7 氨氮的单指标测度函数 Fig. 7 Uncertainly measurement function of ammonia nitrogen |
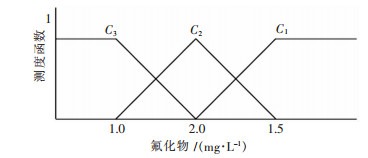 |
| 图 8 氟化物的单指标测度函数 Fig. 8 Uncertainly measurement function of fluoride |
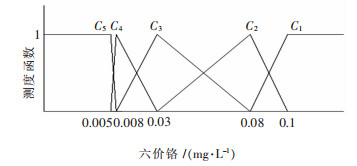 |
| 图 9 六价铬的单指标测度函数 Fig. 9 Uncertainly measurement function of hexavalent chromium |
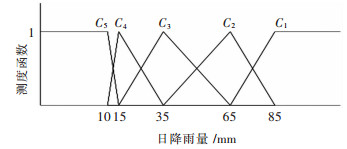 |
| 图 10 日降雨量的单指标测度函数 Fig. 10 Uncertainly measurement function of daily rainfall |
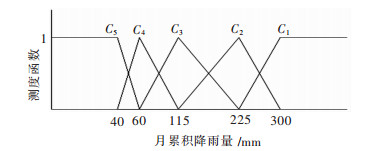 |
| 图 11 月累计降雨量的单指标测度函数 Fig. 11 Uncertainly measurement function of Monthly cumulative rainfall |
2 模型运用
某稀土矿位于我国南部,矿区东西长6.5 km,南北宽4.5 km,呈“Ⅴ”字型.矿区范围面积为10.09 km2.溪流总体上自西向东从矿区西端流至中部的河流,转为往东南流,之后流出矿区.由于在每个矿段实际开采时分片区与矿块进行开采,在开采矿块内通过注液孔将浸矿液注入该矿块所属的某个地下水单元内,这些浸矿液成为开采矿块范围的地下水补给源,同时单元内的地下水从分水岭或高位区径流进入该矿块也形成了补给源[7].开采矿块内的地下水获得了2个方面的补给,并向低水位区径流,除了流向排泄边界也可能流向统一地下水单元内其他矿块.在排泄区以下降泉或泄露成泉的形式排泄,或者进入相连矿块,在覆盖层中以蒸发或散流的形式渗出地表,尤其是浸矿液从注液孔注入时,在较大的水力梯度作用下,除了下渗还在注液孔之间可能发生快速地渗漏,并在坡脚残坡积层或全风化层中较集中地渗漏出来.
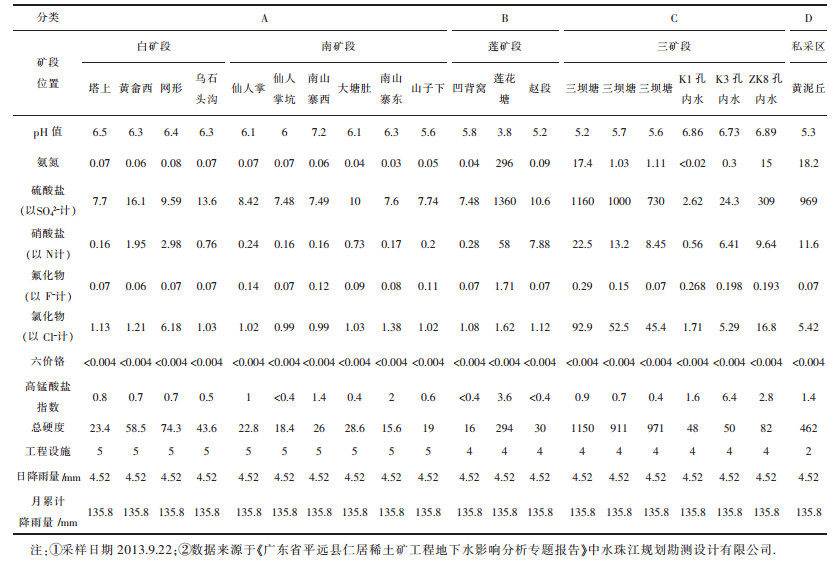
根据前面所建立的未确知测度理论模型,对这一时间段内原地浸矿地下水污染危险性进行评价.开采矿区浸矿前(A矿段)选择了10个观测点,监测11个定量指标,2009年以前开采的老矿区(B矿段)选择了3个观测点,监测11个定量指标,选取2013年9月下旬正在开采矿段(C矿段)6个观测点,监测11个定量指标,对2009之前的私采矿段(D矿段)选择了1个观测点监测11个定量指标,所有监测点的定量数据详见表 3,工程设施属于定性指标,这3个定性指标的赋值依据表 2分别对A、B、C、D 4个矿段进行赋值.将A、B、C、D 4个矿段不同监测点监测的数据采用平均值进行数据处理,经过处理后的数据见表 4.
| 表 3 某稀土矿地下水水质现状监测数据汇总表(pH为无量纲) Table 3 A rare earth mine groundwater quality monitoring data summary table /(mg·L-1) |
 |
| 点击放大 |
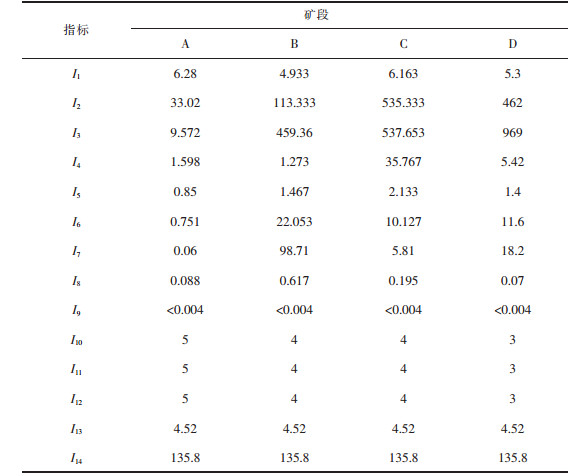
| 表 4 某矿区4个矿段稀土原地浸矿地下水污染评价指标平均处理后的数值 Table 4 Index value of groundwater pollution in situ leaching evaluation at three ore sections in a mining area |
 |
| 点击放大 |
将表 4中矿区4个矿段的各个指标值带入图 1~图 11相应的单指标未确知测度函数中,应用式(10)计算求得4个矿段的单指标评价矩阵:
A、B矿段的单指标评价矩阵分别为:

|

|
C、D矿段的单指标评价矩阵分别为:

|

|
应用信息熵法计算各个指标的权重,由式(8)和式(9)运算求得各指标权重,具体如下:
A矿段指标权重为:
W1=V1/V=0.632/12.905=0.051
W2=W3=…=W6=W8=W9…=W13=1/12.905=0.077
W7=V7/V=0.574/12.905=0.046
W14=V14/V=0.699/12.905=0.056
B矿段指标权重为:
W1=W2=W3=W4=W7=W8=W9…=W12=W13=V1/V=1/13.206=0.076
(W5=V5/V=0.849/13.206=0.063
W6=V6/V=0.658/13.206=0.049
W14=V14/V=0.699/13.206=0.052
C矿段指标权重为:
W1=V1/V=0.724/12.285=0.059
W2=V2/V=0.626/12.285=0.052
W3=W4=W7=W8=W9=…=W12=W13=V3/V= 1/12.285=0.081
W5=V5/V=0.592/12.285=0.049
W6=V6/V=0.644/12.285=0.053
W14=V14/V=0.699/12.285=0.058
D矿段指标权重为:
W1=W3=W4=W6=W7=W8=…=W12=W13=1/13.115=0.076
W2=V2/V=0.618/13.115=0.048
W5=V5/V=0.794/13.115=0.062
W14=V14/V=0.699/13.115=0.054
由求得的指标权重向量、式(10)及上面求得的单指标评价矩阵,可求得某矿区各个矿段的多指标综合测度评价向量:
A矿段多指标综合测度评价向量μ5={0,0.014,0.15,0.066,0.77}
B矿段多指标综合测度评价向量μ5={0.228,0.012,0.123,0.274,0.363}
C矿段多指标综合测度评价向量μ5={0.162,0.078,0.188,0.329,0.243}
D矿段多指标综合测度评价向量μ5={0.304,0.249,0.175,0.044,0.228}
取置信度λ=0.5,在水污染评价中,评价等级越高,发生水污染的风险就越小.根据多指标综合测度评价向量的式(10)以及置信度评价准则的式(11),可知,A矿段k0=0+0.014+0.15+0.066+0.77=1 > λ,即评价对象A矿段的水污染评级等级为Ⅴ级,表明该矿段水质无污染;B矿段k0=0.228+0.012+0.123+0.274=0.637 > λ.即评价对象B矿段的水污染评级等级为Ⅳ级,表明该矿段水质污染的危险性较低,C矿段k0=0.162+0.078+0.188+0.329=0.757 > λ.即评价对象C矿段的水污染评级等级为Ⅳ级,表明该矿段水质污染的危险性较低;D矿段k0=0.304+0.249=0.553 > λ,即评价对象D矿段的水污染评级等级为Ⅱ级,表明该矿段水质污染的危险性较高.
通过以上的计算表明,A矿段位于矿区上游,没有污染. B矿段和C矿段水污染评级等级为Ⅳ级,存在轻微污染,D矿段水质污染的危险性较高,该结果与矿区实际情况较吻合.原地浸矿地下水污染主要来源是由于浸矿过程中使用大量硫酸铵浸矿液,如果矿区存在裂隙或收液系统不完备,都可能导致地下水污染.由于该矿区自2009年被国有上市公司整合后,对原地浸矿开采工艺以及布矿巷道实施企业标准化操作,原地浸矿开采对地下水的影响范围主要集中在开采区的水文地质单元内及其下游一定范围内,对下游大面积范围及其他水文地质单元的地下水影响较小;由表 3实际监测数据可知,正开采矿区地下水氨氮浓度超标,说明原地浸矿开采浸矿液下渗含水层以后,明显提高了开采区水文地质单元内地下水的氨氮浓度,存在轻微污染.开采结束后,随着时间的推移,污染范围逐渐后退,污染逐步消减.然而,私采矿段没有严格执行原地浸矿标准化操作,收液系统简陋,使地下水存在一定污染,污染范围逐渐后退的持续时间长,污染消减较慢.
3 结论1)运用该模型对国内某稀土原地浸矿前、浸矿中、浸矿后以及私采矿区分别进行了地下水污染风险定量评价,评价结果与该矿山的实际情况较吻合.可为矿山企业的环境安全生产提供指导,对地下水污染防治提供了一种新思路.
2)从评价中可以看出,尽管私采矿区的开采工艺采用了原地浸矿技术,但由于原地浸矿防渗工程不够健全,存在地下水污染的风险,且风险级别较高.因此,在原地浸矿开采前应做好矿区构造普查工作,探明稀土矿体底板裂隙,做好矿井巷道布置和防渗工程,尽快推出《离子型稀土原地浸矿开采技术规范》行业标准,并责令稀土开采企业严格按照开采技术规范执行.
3)为更好地验证模型的正确性和普适性,还需对更多的稀土开采企业进行原地浸矿地下水污染风险性调研,进一步完善地下水污染评价指标体系,以进一步验证该模型的普适性和可靠性.
| [1] |
马国霞, 王晓君, 於方, 等. 我国稀土资源开发利用的环境成本及空间差异特征[J].
环境科学研究, 2017, 30(6): 817–824.
|
| [2] |
秦东, 计策. 六汤稀土矿开采过程中存在的问题及应对措施[J].
大众科技, 2011, 140(4): 120–122.
DOI: 10.3969/j.issn.1008-1151.2011.04.055.
|
| [3] |
肖智政, 汤洵忠, 王新民, 等. 底板深潜式离子型稀土矿原地浸析采矿实验研究[J].
化工矿物与加工, 2003, 32(11): 9–11.
DOI: 10.3969/j.issn.1008-7524.2003.11.004.
|
| [4] |
游宏亮. 对离子型稀土保护性开发的建议[J].
问题与建议, 2009, 309(11): 40–42.
|
| [5] |
郑伟强.广东省平远县仁居稀土矿年产1000吨混合稀土(氧化物)项目可行性研究报告[R].广州: 广东省冶金建筑设计研究院, 2012.
|
| [6] |
郑伟强.广东省大埔县五丰矿及扩大区稀土矿年产500吨混合稀土(氧化物)可行性研究报告[R].广州: 广东省冶金建筑设计研究院, 2012.
|
| [7] |
李振嵩, 丁秀平.广东省平远县仁居稀土矿工程地下水影响分析专题报告[R].中水珠江规划勘测设计有限公司, 2013: 66.
|
| [8] |
王光远. 论不确定性结构力学的发展[J].
力学进展, 2002, 32(2): 205–211.
DOI: 10.3321/j.issn:1000-0992.2002.02.005.
|
| [9] |
彭康, 李夕兵, 王世鸣, 等. 基于未确知测度模型的尾矿库溃坝风险评价[J].
中南大学学报(自然科学版), 2012, 43(4): 1447–1452.
|
| [10] |
董陇军, 王飞跃. 基于未确知测度的边坡地震稳定性综合评价[J].
中国地质灾害与防治学报, 2007, 18(4): 74–78.
DOI: 10.3969/j.issn.1003-8035.2007.04.016.
|
| [11] |
栾婷婷, 谢振华, 吴宗之, 等. 基于未确知测度理论的排土场滑坡风险评价模型[J].
中南大学学报(自然科学版), 2014, 145(5): 1612–1617.
|
| [12] |
杜文. 离子型稀土原地浸矿工艺对环境影响的研究[J].
江西有色金属, 2001, 15(1): 41–44.
DOI: 10.3969/j.issn.1674-9669.2001.01.013.
|
| [13] |
祝怡斌, 周连碧, 李青. 离子型稀土原地浸矿水污染控制措施[J].
有色金属(选矿部分), 2011(6): 46–49.
DOI: 10.3969/j.issn.1671-9492.2011.06.012.
|
| [14] |
郑伟强. 原地浸矿采矿法氨氮对环境影响及控制措施[J].
现代矿业, 2015, 556(8): 161–164.
DOI: 10.3969/j.issn.1674-6082.2015.08.053.
|
| [15] |
阳富强, 吴超. 基于未确知测度理论的硫化矿石爆堆自燃危险性评价[J].
中南大学学报(自然科学版), 2010, 41(6): 2373–2380.
|
| [16] |
位振亚, 罗仙平, 梁健, 等. 地下水污染检测技术研究进展[J].
有色金属科学与工程, 2018, 9(2): 103–108.
|
 2018, Vol. 9
2018, Vol. 9


