| 基于测量机器人的露天矿边坡变形在线分析与预测 |
2. 广东省有色地质测绘院,广州 510080
2. Guangdong Nonferrous Metals Surveying and Mapping Institute, Guangzhou 510080, China
滑坡地质灾害一直是矿山开采作业的最大威胁,其频繁的发生对作业人员的生命和财产造成严重影响.尽管近年来在矿山边坡(下文简称边坡)变形监测技术上已经取得了长足的进步,但是仍有一些问题没有彻底解决.其主要包括:①受地形条件的限制,监测技术应用难度较大,成本较高[1]. ②自动化程度低.在监测任务量大的情况下,耗时周期长、数据精度低,无法实现实时测量与监测成果同步化[2].③形变分析理论研究不够深入.因此,为了适应现代边坡工程的监测要求,边坡变形监测技术的发展方向应逐渐体现自动化、远程监测、无线传感、分布式、高精度等[3]特点,从而实现边坡形变监测在时间上的连续观测、空间上的无缝覆盖以及结果的高精度[4].
目前,对矿山进行在线监测的方式有很多,主要包括测量机器人、GPS和微波雷达等[5].例如,徕卡公司的APSWIN自动极坐标系统[6];孙华芬[7]建立的尖山磷矿自动监测系统;任月龙等[4]将GPS、测量机器人、微波雷达有机结合,形成的多传感器监测网;吴站广等[8]基于物联网三层架构与测量机器人技术构建的地下工程测量机器人远程变形监测系统.文中以TM30为基础,引入一种实时、高效的边坡自动变形监测分析与预测技术应用于在矿区边坡变形中,从时间和空间上分析与挖掘边坡变形规律,及时预警预测边坡变形趋势,为矿山开采作业提供了有力保障.
1 研究方法变形区的稳定性分析与实时预测是该技术的核心组成部分,通过对监测点进行形变分析,可以实时、动态掌握边坡的变化规律与动态特征,其分析结果直接影响到形变稳定性判断[9].在获取到差分改正后的监测点坐标信息后,对水平方向和垂直方向上的监测点实现表面位移分析以及形变速率分析,同步生成滑坡观测点位移与沉降综合曲线图等反映变形过程的图表,在变形量异常或者达到预警值情况下,及时将预警信息通过邮件发送给测量人员,并根据变形情况,实时调控监测频率以及监测精度(测回数).如果监测点观测数据缺失,系统将自动对缺失数据采用插值方法进行拟合补全.完成对变形区的形变分析后,运用统计模型对边坡监测数据进行合理的预报,准确、有效的预测边坡的发展趋势.文中根据变形区实际情况,采用经典的GM(1, 1)[10]静态周期模型模拟、预测边坡的失稳状况,并根据模型参数,决定模型预测周期的长短,确定滑坡可能发生的时间节点,为工程施工提供科学的决策依据,避免安全事故的发生,减少经济损失.
1.1 矿山边坡形变分析原理若测站点O的坐标为(X0、Y0、Z0),经过对监测点P进行距离差分改正、斜距化平距和高差、方位角差分改正后,按极坐标测量法公式求出P点的三维坐标值为:
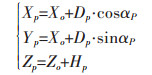
|
Dp为斜距化平距后的水平距离(mm),αP为改正后的方位角(°),HP为经过球气差改正后的三角高差(mm).将第1周期经过差分改正后的P点三维坐标(XP1、YP1、ZP1)设为原始值,则第t周期P点在水平和垂直方向上的累积位移变化量可表示为:
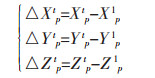
|
其中,△XPt、△YPt为监测点P在第t周期水平方向上的累积位移变化量(m),△ZPt为P点在第t周期垂直方向上的累积沉降变化量(m),XPt、YPt为P点在第t周期的水平坐标值(m),ZPt为P点在第t周期的高程值(m).
设P点在第t-1周期的三维坐标为(XPt-1、YPt-1、ZPt-1),那么P点在第t周期的速率变化量为:
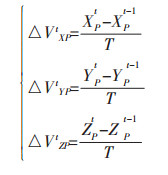
|
其中,T表示2个测量周期的间隔时间(day),△VXPt、△VYPt为P点在第t周期水平方向上的速率变化量(m/d),△VZPt为P点在第t周期垂直方向上的速率变化量(m/d).
1.2 矿山边坡形变分析过程优化自动化监测过程中,由于受到外界和自身因素的干扰,可能会发生棱镜被遮挡、网络信号不稳定等情况,从而导致观测数据无法获取或传输中断.如果TM30对目标点测量8次还是没有返回观测数据,将判定该点在当前周期的监测数据丢失,转而对下一个目标点进行监测.因此,在监测点数据不完整的情况下,为了能真实反映监测点的变形情况,对计算累积位移变化量、速率变化量的算法进行了优化处理是必要的.计算监测点P第t周期累积位移变化量时,以升序方式循环遍历1~(t-1)周期的监测数据,若迭代到第n(1≤n≤t-1)周期,P点数据存在,将判定以第n周期的P点三维坐标值作为初始值,累积位移变化量Sp=S-Sn,将第t周期的Sp与累积位移变化量预警值相比较,若超限,则发出邮件预警并记录报表.在以上条件成立的情况下,若n~(t-1)周期内有P点的三维坐标值缺失,产生非连续性时间监测数据集,将自动采用临近点线性插值[4]方法对缺失的监测数据进行补全,为预测模型提供完整的原始监测数据序列,至此,循环结束.如果遍历到t-1周期都不存在P点,则将第t周期的P点视为初始值,累积位移变化量为0.计算第t周期速率变化量时,以降序方式循环遍历(t-1)~1周期的P点,若迭代到第t-1-n(0≤n < t-1)周期,P点存在,那么速率变化量△VP=(S-St-1-n)/(n+1),循环结束.如果遍历到第1周期还未搜索到监测点P,循环自动结束,第t周期的P点将视为初始点,速率变化量为0.
1.3 基于GM(1, 1)的矿山边坡预测模型建立灰色模型是一种用于分析信息不确定性和不完全性系统的数学方法,它把一切随机过程看作是一定范围内变化的、与时间有关的灰色过程[11].采用GM(1, 1)这种数列模型作为边坡变形监测的预测模型,对原始数据进行累加或者累减处理,寻找系统变动的规律,生成较强规律性的数据序列,然后建立相应的微分方程模型,从而预测未来某一时刻的特征量,进而掌握监测区域变化趋势[12].
1.3.1 GM(1, 1)系统建模选取监测点P的n(n>4)个监测周期的累积位移变化量作为原始序列,n为序列的长度,设观测数据序列x(0)为:
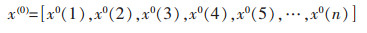
|
对x(0)通过一次累加生成新序列x(1):
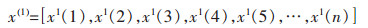
|
根据x(1)可以得到GM(1, 1)模型对应的微分方程为:
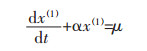
|
(1) |
式(1)中,α为发展灰数,根据α的值来考虑GM(1, 1)模型的适用性[13].其适用范围如表 1所列.
| 表 1 GM(1, 1)的模型适用性 Table 1 Model Applicability of GM(1, 1) |
 |
| 点击放大 |
μ为内生控制灰数.设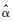
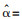
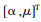
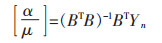
|
(2) |
其中,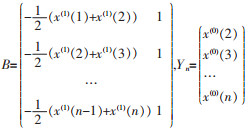
将式(2)中解得的参数α、μ代入到式(1)中求解微分方程,得到x(1)的时间响应函数为:
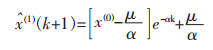
|
之后对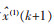
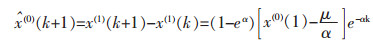
|
(3) |
若k∈(0,n),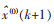
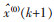
为了提高GM(1, 1)的模型的预测效果,需要对模型的精度进行检验,以评价预测模型的优劣性[15].灰色模型的精度通常使用后验差方法进行检验,即对残差分布的统计特征进行检验,它由相对误差(Δ)、后验差比值C、小误差概率p 3个指标共同评定[11].
1)相对误差[16](Δ)是原始监测数据序列x(0)与预测数据序列
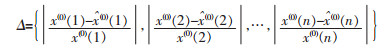
|
2)后验差比值C为预测残差方差S22与原始监测数据方差S12的比值:

|
(4) |
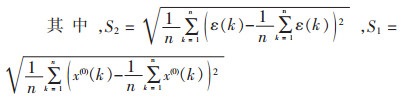
|
(5) |
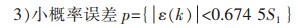
|
(6) |
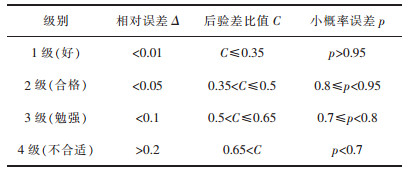
GM(1, 1)模型精度等级分为4级,各等级指标标准如表 2所列.
| 表 2 GM(1, 1)模型精度标准表 Table 2 GM(1, 1) model accuracy standard table |
 |
| 点击放大 |
2 研究区域概况
广州市某石灰石矿山占地面积133.3 hm2(2 000亩),矿区地貌形态属低山丘陵地带,由东面的飞鼠岩(149.9 m)、门口岭、罗山岭(139.8 m)、南面的中洞岭(155.2 m)与西面的大虎坑岭(204.2 m)等低山环绕,地势较高,中部为山间凹地,呈狭长条带状.矿区总体地势南高北低,地形呈开口状“U”字型由南向北展布,东北面有巴江河穿过,汇入珠江,形成山前洪冲积带,平坦开阔,地势较低.
矿山经过近20年来的露天开采,目前采空区形成深凹陷的椭圆形深坑,南北长约750 m,东西长约450 m,最低处高程达-36 m;周边高边坡,边坡与开采区高差均在100 m以上,西边(大虎坑岭)达200 m以上.采空区北边的入口比邻多个大面积的水坑或水塘.随着开采的不断深入,周边边坡高差逐渐加大,若遇雨季,积水坑水也会向采空区渗透,这些不利因素,越来越成为影响开采区稳定的潜在威胁,根据矿区开采计划,将会在矿区中段开采区继续向下挖20 m,但中段的边坡可能会因为开采作业而发生崩塌的危险,因此开展矿区及边坡安全监测工作意义重大,通过对矿区开采区周边边坡进行长期变形监测,获取各坡面的基础数据,分析与预测边坡的稳定性状况,为矿山综合开发及治理等各项决策提供科学依据. 图 1所示为矿区工程地形图.
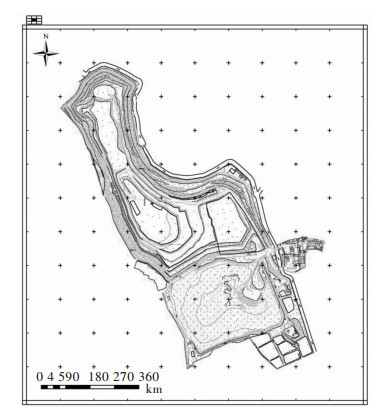 |
| 图 1 矿区地形剖面 Fig. 1 Mine terrain map |
3 矿区边坡时空形变分析 3.1 监测点位布设
为了验证系统的可靠性,将对研究区边坡展开自动监测试验.在监测试验开始前,需布设矿山监测网,监测网的布设秉承有效监测范围广、投入成本低、监测精度高为设计原则[17].通过对石灰矿滑坡地段进行实地考察后,在主要的监测地段-矿区中部相对高程为45 m、65 m、85 m的分层平台上设置3条测线,并在变形体的关键部位,沿着测线两侧5 m范围内地质、地貌特征点位置设立共35个监测点,每个平台至少有1个监测点靠近边坡顶,1个靠边坡脚,监测点之间的间距在30 m以内.在每条测线两端向外延伸100 m的变形区外围稳定区域安置具有强制对中观测墩的基准点,对中误差不超过±0.1 mm,便于TM30搜索、照准目标,为监测点提供高精度的监测数据以及为差分改正起算参考点,每条测线左右两端各1个基准点,共安置6个基准点.测站点的选取上,选择具有良好的通视性和稳定性的区域用水泥浇筑成观测墩固定TM30[18],作为极坐标系统的原点,在对矿区地形进行分析后,决定选择在滑坡对面西南方向250 m山腰视野开阔处安放测量机器人.
3.2 数据的来源与处理为快速、精准的获取边坡监测数据,文中以SQL Server 2008为数据库、Visual Studio 2012为编译平台,在徕卡TM30的基础上,将极坐标测量法与计算机工程有机结合研发与设计了矿山边坡在线监测与分析系统(下文简称系统),自动对矿区进行全天候不间断的无人监测,由TM30对观测的水平角、垂直角、斜距等数据为主要数据来源,此外,由于测量机器人观测范围受地形因素影响较大,因此存在一些观测死角,采用高精度位移传感器[19]配合DTU[20]无线通讯模块采集观测死角目标点的变形数据作为次要数据来源.
合理的数据处理方式是获取高精度监测数据的关键.通过极坐标表达式对目标点的方位角、垂直角以及斜距值进行解算,得出目标点三维坐标值用以分析与预测边坡稳定性.但在实际测量过程中,研究区范围内的温度、大气折光、气压、空气扰动等环境因素会对基准点、监测点以及测站造成微动变化[21],从而造成测量误差.因此,在计算目标点坐标时,必须考虑到气象因素对观测精度的影响[22].利用实时差分改正技术,在不测定矿区气象环境的条件下,以矿山基准网为基础,改正目标点的距离、高差和方位角.把小范围内基准点与监测点的气象条件看作是相同的,计算每个测量周期观测的测站点到基准点的测量值与初始值的差值,该差值就被认为是环境因素所造成的误差,将此差异加到监测点的观测值上进行差分处理,可将监测精度提高到亚毫米级[23].
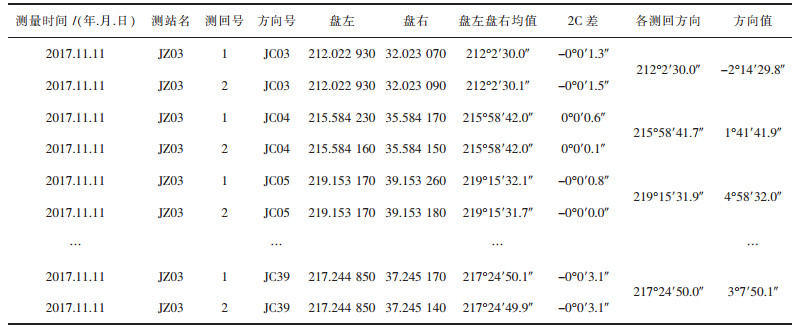
3.3 监测成果分析与评价此次监测试验从2017.10.30日起至2017.11.21结束,设定监测周期间隔时间为1天,每天的监测时间为8:00至14:00,测回数为2,单个监测周期约为20~30 min,X、Y、Z方向累积位移预警值为30 mm,变形速率预警值为3 mm/d.预测功能在监测周期达6个以上开启,并将预测等级分为安全、警告、危险3个级别,对于变形监测过程中超限的数据以及达到警告和危险级的预测信息,系统将自动发出邮件预警,部分原始监测数据如表 3所列.
| 表 3 部分原始监测数据表 Table 3 Partial raw measurement data table |
 |
| 点击放大 |
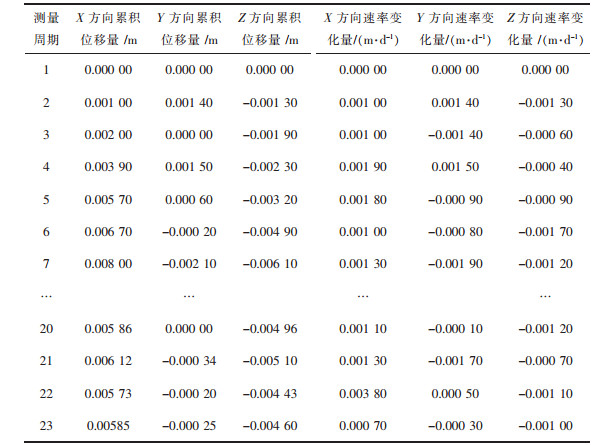
选取矿区西段65 m高程的监测点JC03的23期观测数据为例对矿区边坡形变进行分析,其监测成果如表 4及图 2(a)~图 2(b)所示.
| 表 4 JC03点监测成果表 Table 4 JC03 point monitoring results table |
 |
| 点击放大 |
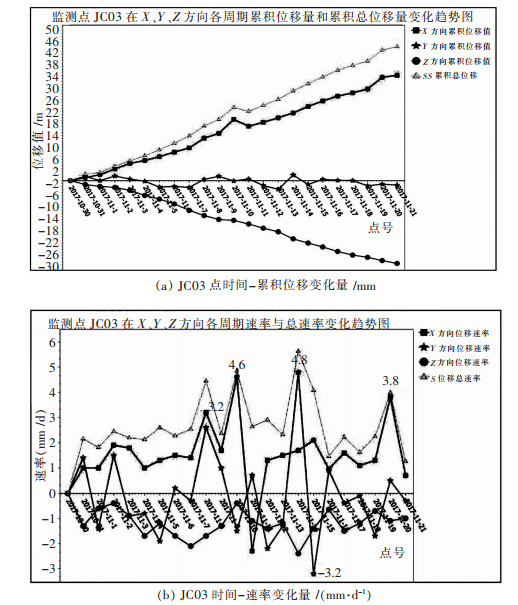 |
| 图 2 监测点JC03在X、Y、Z方向累积位移与速率变化趋势 Fig. 2 Trend of cumulative displacement and velocity change of monitoring point JC03 in X、Y and Z directions |
图 2通过对监测时间进行插值,实现在时间序列上的连续性,直观反映出JC03的累积位移变化量与速率随着时间变化的趋势.试验结果表明,JC03点在X方向和Z方向的累积位移变化量表现出有规律的变化,Y方向上则在上下来回波动,无明显规律. JC03点在X方向上的速率变化基本大于0,说明X方向的累积位移变化量在往正方向增大,Z方向上的速率变化为负,表示位移增量在负增长,Y方向则无明显规律.总体来说,监测点JC03在水平方向上往正东偏移,在19日达到了预警值,而且偏移趋势正在变大,系统发出警报,在垂直方向上,监测点在往负方向偏移,表明整个监测区地基正在下沉,在21日达到了27.6 mm,并有继续扩大偏移的趋势,未来几天将达到预警值.
通过对观测区内所有监测点在任意监测周期对其位移变化量进行空间插值处理,可随时动态掌握任意时刻整个变形区连续空间分布的监测结果,反映矿山开采作业对矿区边坡变形的影响,实现边坡监测的空间无缝性.在对第23周期所有监测点的位移累积量做空间插值后可以直观的显示出变形的分级效果,如图 3(a)~图 3(b)所示,第23周期TM30观测的37个监测点的相对坐标,监测点的坐标是通过在矿山周围稳定区域建立独立基准网,由TM30周期性的自动观测监测获取.从图 3中可以看出,不管是从水平方向还是垂直方向上,变形的部位集中在变形区的西部以及中部的散点区,越靠近开采区底部的边坡区域,变形量是大于远离开采区的边坡变形量,说明矿山开采对边坡变形的影响很大.
 |
| 图 3 基于空间插值的矿区形变结果 Fig. 3 Deformation result of mining area based on spatial interpolation |
4 边坡变形实时预测
文中以监测点JC03为例,以垂直方向上的6个观测周期(2017-11-16至2017-11-21)累积位移量作为原始观测序列来建立GM(1, 1)模型.设置30 mm累积位移变化量为警告预警线,35 mm为危险预警线,其原始序列x(0)为:
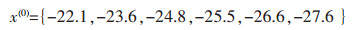
|
通过一次累加后生成新序列x(1):
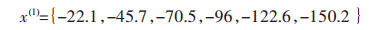
|
利用最小二乘法求得待定系数:
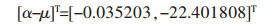
|
根据表 1可知,0.3<α=0.035 203<0.5,所以该模型可以对边坡进行短期预测.将α、μ代入微分方程中求得时间函数表达式,并将α、μ代入到式(3)作累减计算得到监测点JC03的预测模型为:
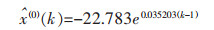
|
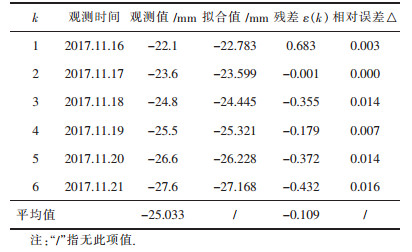
当观测周期k≤6时,监测点JC03在Z方向累积位移观测值与拟合值如表 5所列.
| 表 5 监测点JC03在Z方向累积位移观测值与拟合值 Table 5 Cumulative displacement observations and predicted values of monitoring point JC03 in the Z direction |
 |
| 点击放大 |
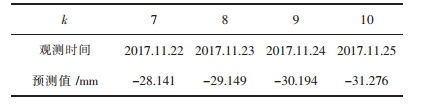
当观测周期k > 6(即第7至第10周期)时,使用前6个周期的观测值来预测监测点JC03后4个周期累积位移变化,其预测值如表 6所列.
| 表 6 监测点JC03在Z方向累积位移预测值 Table 6 Cumulative displacement predicted value of monitoring point JC03 in Z direction |
 |
| 点击放大 |
根据表 6中的预测值可知,如果不采取有效的预防措施而选择继续开采作业,那么预计在2017.11.24,沉降累积变形量将超过30 mm警告线并继续增大,很快就会达到35 mm的危险线,边坡具有塌方的危险,应提前做好预防工作.为了提高模型预测的精确性,还需由相对误差△、后验差比值C、小误差概率p来对GM(1, 1)模型进行精度检验.
由表 5可以得出观测值中值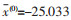
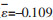
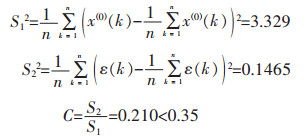
|
小误差概率p由式(6)可计算得到:
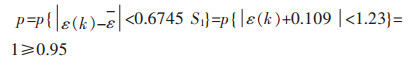
|
查看表 2的模型精度等级可知,模型等级为一级,预测效果良好. 图 4(a)~图 4(c)为监测点JC03~JC05在Z方向上累积位移观测值与预测值的变化趋势.
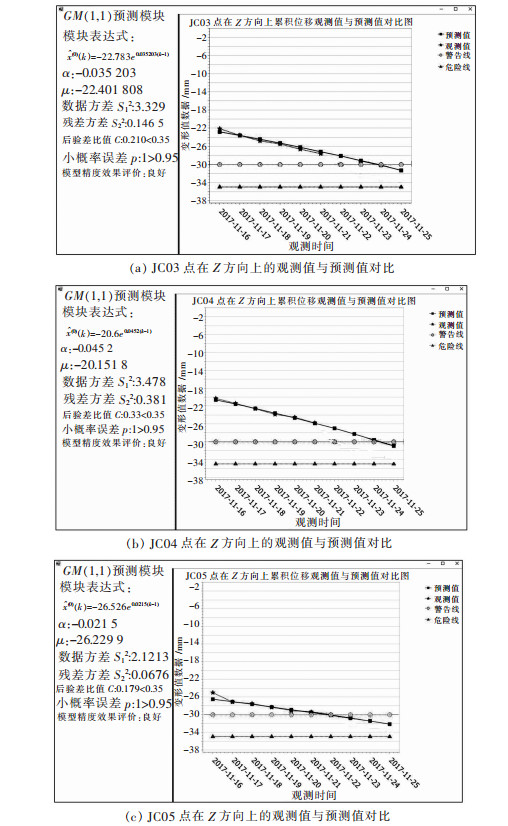 |
| 图 4 监测点JC03~JC05在Z方向累积位移观测值与预测值变化趋势 Fig. 4 Point JC03~JC05 cumulative displacement observation value and predicted value change trend diagram in Z direction |
5 结论
事实证明,将露天矿边坡变形在线分析与预测技术应用于矿区边坡变形监测中是可行的,由计算机控制测量机器人对矿区进行全天候、长航时、高精度的自动化测量,实现了在无人环境下独立完成观测、入库、计算、分析与预警预测等工作,具有自动化、智能化、超远程、低成本、操作简单、通用性强等特点,满足了现代变形监测技术所需的远程无人的自动化测量、科学稳定的数据管理、精确高效的数据处理、实时合理的预测预报要求.该技术不仅适用于矿山边坡的监测工作,对于大坝、深基坑、桥梁、隧道等变形也同样适用.今后拟在现阶段完成工作的基础上,对该技术做进一步完善;①考虑采用测量机器人与多传感器(例如位移传感器、沉降传感器、GPS等)相结合的模式,信息互补与数据相互印证,进一步提高监测精度;②采用多种预测模型对边坡进行预测,避免单一模型预测所带来的适用性问题,导致预测效果差,通过加入影响边坡变形的气象因子、地质因子等参数,使得模型预测更加精准.
| [1] |
董文文, 朱鸿鹄, 孙义杰, 等. 边坡变形监测技术现状及新进展[J].
工程地质学报, 2016, 24(6): 1088–1095.
|
| [2] |
马大喜, 肖海平. 矿山变形监测数据管理系统的开发[J].
江西有色金属, 2006(4): 35–37.
DOI: 10.3969/j.issn.1674-9669.2006.04.011.
|
| [3] |
李爱国, 岳中琦, 谭国焕, 等. 香港某边坡综合自动监测系统的设计和安装[J].
岩石力学与工程学报, 2003(5): 790–796.
DOI: 10.3321/j.issn:1000-6915.2003.05.019.
|
| [4] |
任月龙, 李如仁, 张信. 基于多传感器网的露天矿边坡形变监测[J].
煤炭学报, 2014, 39(5): 868–873.
|
| [5] |
陈丽.面向大型结构的调频连续波雷达位移测量系统VCO及回波的影响研究[D].重庆: 重庆大学, 2015.
http://cdmd.cnki.com.cn/Article/CDMD-10611-1015967567.htm |
| [6] |
赵先奎. 特种钢结构建筑测量—自动极坐标测量系统在钢结构安装测量中的运用[J].
建筑施工, 2005(10): 23–25.
DOI: 10.3969/j.issn.1004-1001.2005.10.008.
|
| [7] |
孙华芬.尖山磷矿边坡监测及预测预报研究[D].昆明: 昆明理工大学, 2014.
http://cdmd.cnki.com.cn/Article/CDMD-10674-1014349085.htm |
| [8] |
吴战广, 张献州, 张瑞, 等. 基于物联网三层架构的地下工程测量机器人远程变形监测系统[J].
测绘工程, 2017, 26(2): 42–47.
|
| [9] |
周才文.基于地面三维激光扫描的露天矿山边坡变形监测研究[D].赣州: 江西理工大学, 2018.
http://cdmd.cnki.com.cn/Article/CDMD-10407-1018215946.htm |
| [10] |
李梦婉, 沙秀艳. 基于GM(1, 1)灰色预测模型的改进与应用[J].
计算机工程与应用, 2016, 52(4): 24–30.
DOI: 10.3778/j.issn.1002-8331.1506-0257.
|
| [11] |
肖海平, 陈兰兰. 灰色理论模型在矿山变形监测中的应用[J].
金属矿山, 2009(1): 154–155.
DOI: 10.3321/j.issn:1001-1250.2009.01.043.
|
| [12] |
李小燕.灰色神经网络预测模型的优化研究[D].武汉: 武汉理工大学, 2009.
http://cdmd.cnki.com.cn/Article/CDMD-10497-2009102750.htm |
| [13] |
马萍.灰色系统GM(1, 1)模型的改进及灰色统计模型研究[D].长春: 吉林大学, 2007.
http://cdmd.cnki.com.cn/Article/CDMD-10183-2007093681.htm |
| [14] |
唐校, 谢光奇, 谢宁鲁, 等. 基于最小二乘法的灰色模型参数估计[J].
湘南学院学报, 2010, 31(5): 62–64.
DOI: 10.3969/j.issn.1672-8173.2010.05.014.
|
| [15] |
赵一晗, 赵立华. 灰色模型在某水闸变形监测数据处理中的应用[J].
江苏水利, 2010(6): 24–26.
DOI: 10.3969/j.issn.1007-7839.2010.06.011.
|
| [16] |
秦真珍.露天矿边坡变形灰色系统预报模型研究[D].阜新: 辽宁工程技术大学, 2009.
http://cdmd.cnki.com.cn/Article/CDMD-10147-1011024606.htm |
| [17] |
储征伟, 钟金宁, 段伟, 等. 自动化三维高精度智能监测系统在地铁变形监测中的应用[J].
东南大学学报(自然科学版), 2013, 43(S2): 225–229.
|
| [18] |
梅文胜, 张正禄, 黄全义. 测量机器人在变形监测中的应用研究[J].
大坝与安全, 2002(5): 33–35.
DOI: 10.3969/j.issn.1671-1092.2002.05.010.
|
| [19] |
詹建徽, 张代远. 传感器应用、挑战与发展[J].
计算机技术与发展, 2013, 23(8): 118–121.
|
| [20] |
张文, 黄声享, 李洋洋. 基于测量机器人的自动化变形监测系统设计与实现[J].
测绘工程, 2018, 27(2): 37–41.
|
| [21] |
卫建东. 基于测量机器人的自动变形监测系统[J].
测绘通报, 2006(12): 41–44.
DOI: 10.3969/j.issn.0494-0911.2006.12.012.
|
| [22] |
曾勇.基于TS30测量机器人地壳形变自动数据采集系统的研究与应用[D].西安: 西安科技大学, 2014.
http://cdmd.cnki.com.cn/Article/CDMD-10704-1014072729.htm |
| [23] |
蔡乾广.多测站自动变形监测系统研发[D].青岛: 山东科技大学, 2007.
http://cdmd.cnki.com.cn/Article/CDMD-10424-2008013888.htm |
 2018, Vol. 9
2018, Vol. 9


