| 围压对红砂岩应力波频谱和频带能量特性的影响 |
b. 江西理工大学, 资源与环境工程学院, 江西 赣州 341000;
c. 江西理工大学, 江西省环境岩土与工程灾害控制重点实验室, 江西 赣州 341000
b. School of Resources and Environmental Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China;
c. Jiangxi Provincial Key Laboratory of Environmental Geotechnology and Engineering Disaster Control, Jiangxi University of Science and Technology, Ganzhou 341000, China
针对地震频发、工程钻爆开挖以及采矿诱发矿震等自然和人类活动,岩石(体)应力波传播特性及机理是众多学者研究的热点问题,也是研究工程岩体稳定性关键科学问题之一。随着资源开采等人类活动的深度越来越大,围岩体承受的地应力也逐渐增加,岩石物理力学性质发生较大改变,高地应力成为深部工程岩体的本真属性,是工程岩体众多力学特性的决定性因素[1]。故在研究岩(石)体应力波传播特性时,应考虑初始地应力对岩石应力波传播衰减的影响.
大量研究结果表明,静应力对岩石动态强度[2-4]、变形特性、能量耗散[5]、抵抗疲劳冲击性能、破坏类型及机理等都有较大的影响[6-10],适当大小的静应力有助于提高岩石的抗冲击性能[11-13],但以上都属于对力学响应特性的研究,目前有关受载岩石(体)的应力波传播特性的研究相对较少。金解放等[14]利用改进的霍布金逊压杆实验系统,对具有不同轴向静应力的红砂岩长试件进行应力波传播实验,分别研究了轴向静应力对岩石纵波波速、幅值时空衰减系数的影响。刘少虹等[15]进行了室内煤岩组合体应力波传播实验,通过应力波波形、透射系数、反射系数和能量耗散等参数,研究了应力波幅值和静载对煤岩组合体中应力波传播特性的影响。针对地应力节理岩体的应力波传播特性,李新平等[16-17]通过模型实验手段研究深部高应力对工程岩体中应力波传播衰减的影响特性,并通过理论和实验相结合的手段,研究了柱面应力波在受载节理岩体中的传播衰减特性。结果表明,地应力大小对节理岩体应力波传播衰减有较大的影响。范立峰等[18]假设节理岩体变形适应非线性Bandis-Barton(B-B)模型,利用位移不连续方法建立了具有地应力节理岩体的应力波传播模型,分析了受载节理岩体应力波传播的幅值和频率相关性,并重点探索了原岩应力对应力波透射系数、能量传递和有效波速的影响。结果表明,随着原岩应力的增加,应力波透射系数、能量透射系数和有效波速原来越大。上述研究对深部高应力下工程岩体安全高效爆破开挖具有重要的理论和实际意义。然而,目前对围压影响岩石应力波传播衰减特性方面的研究未见报道.
研究岩石(体)中波的传播特性可以通过幅值衰减[15, 19]、透反射系数[16-19]、有效波速[15, 19]、波形分形[20]和频谱分布特征[21-22]等角度表征,前4种表征方法多是岩石(体)弹性波传播衰减的外在现象,频谱和频带能量分布则相对侧重弹性波在岩石(体)中衰减的机理。目前对岩石应力波传播衰减规律研究多从幅值衰减、透反射系数和有效波速进行研究,而对岩石应力波的频谱和频带能量研究较少.
基于动静组合加载试验装置,对具有不同围压的红砂岩试件进行应力波传播试验,试验过程中,轴向静应力为零,围压从零逐渐增大,所有围压工况下的入射波相同,通过分析反射波和透射波的频谱和频带能量的变化,表征围压对岩石应力波传播衰减的影响。通过快速傅立叶变换将反射波和透射波时域信号变换得到应力波频域数据,分析研究围压对岩石反射波和透射波频谱图和主频的影响规律。利用Matlab小波包分析模块进行编程,对反射波和透射波信号进行频带能量分析。研究结果有利于探索静应力下岩石应力波传播衰减规律,并为工程岩体安全,高效爆破、开挖等提供理论参考.
1 试件、试验装置及方法 1.1 试件试件采用完整性和均质性较好的红砂岩。其长度为100 mm,直径为φ50 mm,纵波波速为2390 m/s,单轴抗压强度为52 MPa,为保证岩石试件受力均匀,试件两横截面平整度误差±0.02mm,严格满足岩石力学试验标准。试验使用的应变片尺寸为2 mm×1 mm,其电阻为120Ω±0.1Ω,在入射杆及透射杆上下表面对称黏贴应变片,最大限度消除试件偏心压缩对应力波的影响。为避免采集到的波形相互干扰,如图 1所示,测点1距入射端900 mm,测点2距透射端600 mm.
1.2 试验装置试验装置采用动静组合加载实验系统,其围压系统和冲击系统的动力源相对独立,可以在应力波传播试验前对岩石试件施加不同大小的围压。将岩石试件水平放置在入射杆与透射杆之间,如图 1所示,尽量保证入射杆、试件和透射杆轴线重合。为消除PC振荡,实现半正弦波加载,采用纺锤形异型冲头。由于围压装置真实施加围压段只有100mm,试件必须准确放置围压装置中间,否则会出现漏油现象而导致围压施加失败。为确保弹性杆和试件之间接触良好,并能很好地减小界面摩擦力,试件两端均匀涂抹黄油。放置好试件后,分别将弹性杆上2个测点处的应变片连接到超动态应变仪上.
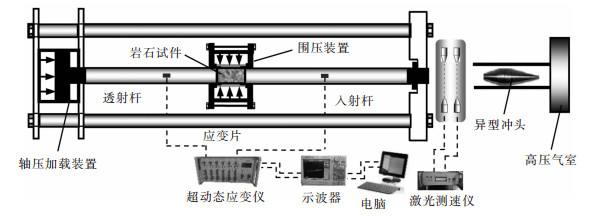 |
| 图 1 具有围压作用的岩石应力波传播试验示意图 Fig. 1 Schematic of stress wave propagation experiment along rock specimen under confining pressure |
1.3 静应力大小和入射波大小
试验过程采用手动油压泵进行围压加载,其压力表最小刻度为2 MPa,便于精确读取围压值,围压大小间隔为4 MPa,其大小分别为0、4、8、…、40 MPa,试验过程保证轴向静载为0 MPa.
为了使不同围压工况下岩石试件的应力波传播特性有可比性,所有应力波传播实验都保证入射波幅值大小相同。实现方法是固定高压气室内的气压、冲头在枪膛内的位置以及开启阀门的速度,冲头的撞击速度大约为4.3 m/s.
2 试验结果分析 2.1 应力波波形通过试验测得试件在不同围压情况下的应力波数据,图 2给出四种围压下的应力波时程曲线。由图 2可以看出,随围压的增加,应力波形状基本一致。为了探究围压对应力波传播的影响,文中将通过反射波和透射波频谱和频带能量来表征应力波传播衰减规律.
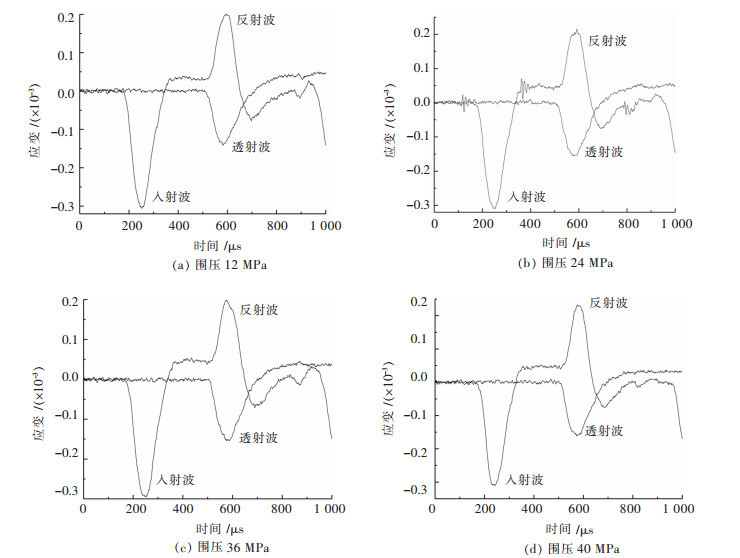 |
| 图 2 不同围压下原始波形图 Fig. 2 Stress wave of specimen under different confining pressure |
2.2 应力波的频谱形状
由图 2可以看出,试验采样时间为1 ms,共采集1000个数据点,因此其采样频率为1 MHz。根据图 2所示的入射波、反射波和透射波的起点和终点时间,确定其各自的应力波时域数据。在Matlab软件中编写快速傅里叶变换程序,分别得到不同围压情况下所有应力波的频谱数据。图 3所示为围压20 MPa时,岩石试件的入射波、反射波和透射波的频谱全图.
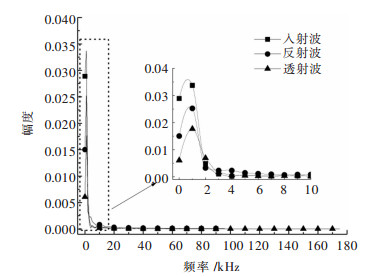 |
| 图 3 围压20 MPa应力波频谱图 Fig. 3 Spectrum of stress wave under 20 MPa confining pressure |
由图 3可以看出,入射波、反射波和透射波的幅度能量主要分布在0~3 kHz之间,为了更好地研究和表征岩石应力波主频和主要频带能量的变化规律,后文将主要分析0~3 kHz之间的频谱数据。图 4所示为不同围压工况下岩石试件的入射波、反射波和透射波在0~3 kHz间的频谱图.
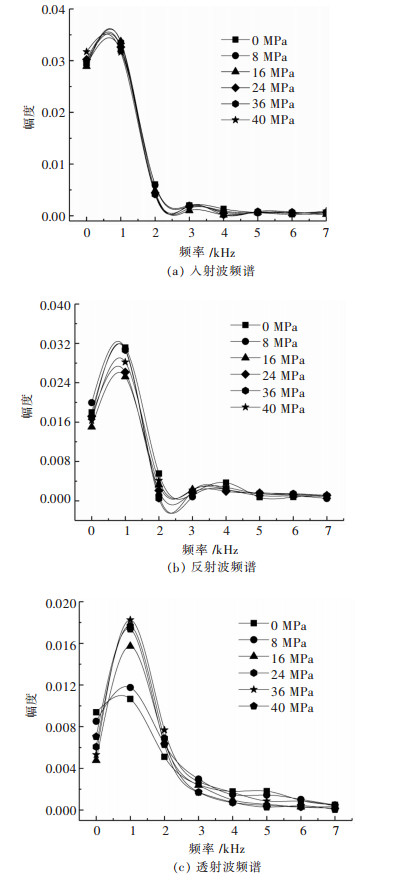 |
| 图 4 不同围压下应力波频谱图 Fig. 4 Spectrums of stress wave under different confining pressure |
由图 4(a)可以看出,不同围压工况下,入射波频谱图形状和大小基本相同。这主要是因为在所有围压工况下,冲头为同一异型冲头,冲头的撞击入射杆的速度相同,且入射杆都无轴向静应力,根据一维应力波理论可知,所有围压工况下的入射波时域数据相同,进而其频域数据也应相同。由于不同围压情况下入射波的频谱相同,可以通过反射波和透射波频谱的变化表征围压对岩石应力波的影响.
由图 4(b)可以看出,所有围压情况下反射波的频谱形状近视相同。随着围压值的增加,反射波频谱图的幅值呈“减小-缓慢发展-增加”的趋势。频谱图幅值对的频率值即认为是应力波的主频值,随着围压的增加,反射波的主频值也在发生改变。由图 4(c)可以看出,随着围压值的增大,透射波的频谱幅值逐渐增大后有略微减小,且宽度也越来越窄.
分析认为,造成反射波和透射波频谱幅值改变的原因在于围压对岩石试件波阻抗的影响。随着围压的增加,先是有助于岩石试件初始孔隙的压密,使试件进入弹性阶段。在这个过程中,岩石试件的密度和纵波波速值逐渐提高,导致其波阻抗值逐渐增大,由于试验过程中没有轴向静应力的约束,当围压增加到一定值时,岩石试件又开始出现损伤现象,导致其波阻抗值下降。围压从零逐渐增加的过程中,岩石试件波阻抗先增加后减小,在相同的入射波情况下,反射波包含的频带能量比值先减小后增加,透射波包含的比值先增加后减小。随着围压的增加,透射波频谱的宽度越来越窄的原因在于高频段的应力波更易衰减造成的.
2.3 应力波的主频根据频谱图中幅值对应的频率值,可以得到岩石反射波和透射波在不同围压情况下的主频值,所有围压工况下反射波和透射波的主频值如图 5所示.
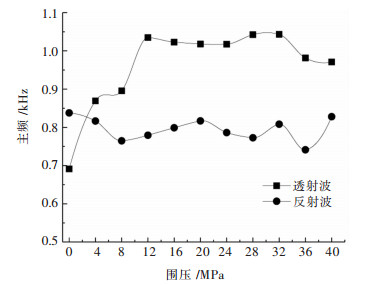 |
| 图 5 应力波主频随围压的变化 Fig. 5 Main frequencies of stress wave under different confining pressure |
由图 5可以看出,围压大小影响反射波和透射波的主频值。在围压从零增加到40 MPa的过程中,透射波主频值呈“快速增加-缓慢变化-下降”的趋势,12 MPa和32 MPa是其两个围压分界值,与单轴抗压强度的比值分别为25%和70%。从快速增加段的斜率可以看出,透射波主频对围压压密岩石初始孔隙过程较敏感.
与透射波的主频值变化相比,反射波主频值呈“减小-缓慢发展”的趋势,与透射波主频值的变化相比,反射波主频值的变化相对较小,即反射波主频对围压的反应不太灵敏.
2.4 应力波频带能量特征在相同的入射波情况下,不同围压时岩石将产生不同的反射波和透射波,研究得到不同围压工况下反射波和透射波中频带能量的变化规律,有助于表征围压对应力波传播特性的影响。利用Matlab中小波包模块,分析反射波与透射波信号的频带能量分布特征,反射波和透射波信号S(t)的表达式为:
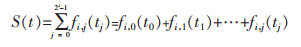
|
(1) |
式(1)中,fi, j(ti)为应力波信号小波包分解到节点(i, j)上的重构信号,j=0, 1, 2, …, 2i-1, (i=1, 2, …, 11).
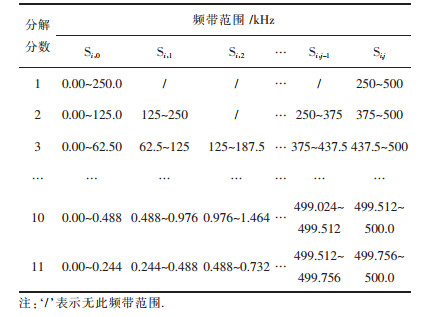
试验过程中示波器采样频率设置为1 MHz,由采样定理知其奈奎斯特采样频率即为500 kHz。对反射波与透射波信号进行11层小波包频带分解,第i 层可以得到2i 个子频带,故应力波信号经过11层小波包频带分解后可以得2048个子频带,相应的最低频带为0.000~244.14 Hz。各层重构信号的频带范围如表 1所示(其中,Si, j表示第i层的第j 个小波包分解系数重构信号).
| 表 1 应力波分解重构系数及各层频带范围 Table 1 Stress Wave Decomposition Reconstructing Coefficients and Bands of Each Layer |
 |
| 点击放大 |
应力波信号经过小波包分解后,提取出不同频带范围内的信号,就能够对不同频带的应力波信号能量的大小及分布情况进行研究。在实际应用中,经常用信号幅值的平方、持续时间的长短或者事件的包络面积等参数来表征。文中使用应力波幅值的平方表征其能量,第i层应力波分量的能量表达式为:
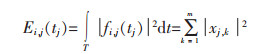
|
(2) |
式(2)中,i为小波包分解的层数,m为离散采样点数,Ei, j(ti)表示信号分解到第j个节点处的小波包频带能量,xj, k(j=0, 1, 2, …, 2i-1, (i=1, 2, …, 11), k=1, 2,…,m)为应力波信号重构信号fi, j(ti)离散采样点的幅值.
应力波信号S(t)为第i层所有节点上重构信号之和,其总能量等于第i层各节点信号分量的能量之和。由式(2)可求得应力波信号S(t)的总能量为:
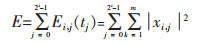
|
(3) |
故原始信号各频带内的能量占信号总能量的百分比Pi, j可表示为:
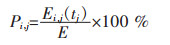
|
(4) |
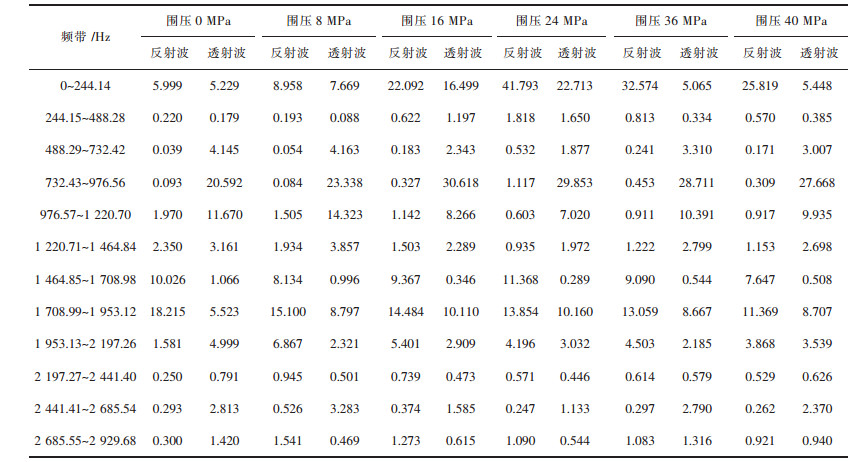
通过式(4)可以求解出应力波信号经分解后各频带能量占总能量百分比情况,由于篇幅有限,表 2仅列出围压为0, 8, 16, 24, 36, 40 MPa六个围压工况下反射波和透射波不同频带的能量百分比.
| 表 2 不同围压工况下反射波和透射波频带能量百分比 Table 2 Frequency band energy percentage of reflected and transmitted waves under different confining pressure |
 |
| 点击放大 |
由表 2可以看出,所有围压工况下,反射波的能量主要分布在0~244.14 Hz和1464.84~2197.26 Hz频带之间,约占其总频带能量的45%以上。透射波的能量主要分布在0~244.14 Hz、488.29~ 1464.84 Hz和1708.99~2197.26 Hz频带之间,约占其总频带能量的60%以上.
为了直观显示0~2929.68 Hz区段内反射波和透射波频带能量的变化规律,列出试验所得部分围压工况下反射波和透射波频带能量百分比分布情况,图 6表示出了反射波和透射波频带能量百分与频带关系.
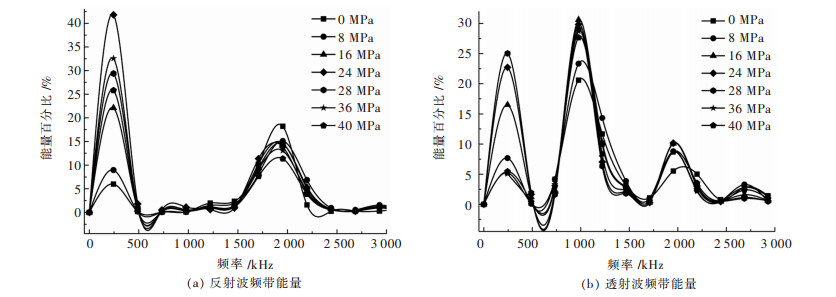 |
| 图 6 不同围压工况下反射波和透射波的频带能量图 Fig. 6 Frequency band energy distribution under different confining pressure |
由图 6(a)可以看出,在0~2929.68 Hz之间,反射波频带能量分布图有两个极值点,分别在244.14 Hz和1953.12 Hz。在第一极值点(244.14 Hz)能量百分比最大,属于主频带。随着围压的增加,主频带能量百分比整体呈先增大后减小的趋势。在第二极值点(1953.12 Hz),能量百分比整体呈先减小后增大的趋势,频带能量百分比变化趋势与第一峰值点相反,且对围压的敏感度降低.
由图 6(b)可以看出,透射波频带能量在在0~2929.68 Hz之间的分布图有4个极值点,依次位于频率为244.14 Hz、976.56 Hz、1953.12 Hz和2685.54 Hz处。从图 6(b)可以看出,前两个极值点(244.14 Hz和976.56 Hz)频带能量百分比较大,属于优势频带区域。在极值点244.14 Hz处,随着围压变化,频带能量百分比也呈先增加后减小的趋势,对应的围压转折点较极值点244.14 Hz时的围压值小。围压对高频带(1953.12 Hz和2685.54 Hz)能量百分比的影响明显低于对低频带(244.14 Hz和976.56 Hz)能量百分比的影响.
对比图 6(a)和(b)可以看出,低围压时频带能量百分比变化幅度较高围压时大,高频处此现象更加明显。分析认为,由于围压对岩石试件影响大致分“压密-弹性-破坏”三个阶段。施加围压初始阶段,岩石试件中初始孔隙对围压较敏感,使得低围压时频带能量百分比变化幅度较大;随着围压继续增大,试件进入弹性阶段。在这个过程中,岩石试件的波阻抗值增大速率较压密阶段变缓,导致频带能量百分比变化幅度减慢。当围压增加到一定值时,岩石试件又开始出现损伤现象,导致其波阻抗值下降,使得该阶段频带能量百分比开始减小。应力波传播时总是高频段波衰减大于低频段波衰减,因此导致出现围压对低频带能量百分比的影响灵敏性较对高频带的影响灵敏性更大这一试验现象.
3 结论基于动静组合加载试验装置,对红砂岩试件进行具有不同围压的应力波传播试验,分析反射波和透射波的频谱和频带能量演化特性,得到如下结论:
(1)当轴向静载荷为零,随着围压值由零增大到40 MPa过程中,岩石反射波频谱图的幅值呈“减小-缓慢发展-增加”的趋势,透射波频谱图的幅值逐渐增大后有略微减小。反射波和透射波频谱图峰值区域比入射波峰值区域的宽度更窄.
(2)随着围压的增加,透射波主频值的变化大致分为三个阶段:增大-稳定不变-减小,围压与单轴抗压强度之比为25%和70%是其两个围压值转折点。反射波主频的变化趋势与透射波主频的变化趋势相反.
(3)入射波频带能量分布图(0~3 kHz)有两个极值点,随着围压的增加,主频带所占总能量百分比先增加后减小。透射波频带能量分布图(0~3 kHz)有四个极值点,随围压的增加,两个优势频带处的能量百分比先增加后减小。无论对反射波还是透射波,围压对低频带能量百分比的影响灵敏性较对高频带的影响灵敏性更大.
| [1] |
谢和平, 高峰, 鞠杨. 深部岩体力学研究与探索[J].
岩石力学与工程学报, 2015, 34(11): 2161–2178.
|
| [2] |
何聪, 金解放, 周学进, 等. 静载荷与循环冲击组合作用下岩石损伤本构模型研究[J].
有色金属科学与工程, 2016, 7(4): 114–120.
|
| [3] |
金解放, 钟海兵, 吴越, 等. 静载荷与循环冲击作用下岩石损伤变量定义方法的选择[J].
有色金属科学与工程, 2013, 4(4): 85–90.
|
| [4] |
黄志辉, 卢春燕, 沈国华, 等. 单轴加载条件下砂岩声发射特性分析[J].
有色金属科学与工程, 2014, 5(1): 91–94.
|
| [5] |
袁伟, 金解放, 梁晨, 等. 围压下混凝土动态损伤与能量耗散特征数值分析[J].
有色金属科学与工程, 2017, 8(4): 98–104.
|
| [6] |
金解放, 李夕兵, 钟海兵, 等. 三维静载与循环冲击组合作用下砂岩动态力学特性研究[J].
岩石力学与工程学报, 2013, 32(7): 1358–1372.
DOI: 10.3969/j.issn.1000-6915.2013.07.010.
|
| [7] |
吕晓聪, 许金余, 葛洪海, 等. 围压对砂岩动态冲击力学性能的影响[J].
岩石力学与工程学报, 2010, 29(1): 193–201.
|
| [8] |
LI XB, TAO M, WU CQ, et al. Spalling strength of rock under different static pre-confining pressures[J].
International Journal of Impact Engineering, 2017, 99: 69–74. DOI: 10.1016/j.ijimpeng.2016.10.001. |
| [9] |
李夕兵, 宫凤强, ZHAO J, 等. 一维动静组合加载下岩石冲击破坏试验研究[J].
岩石力学与工程学报, 2010, 29(2): 251–260.
|
| [10] |
尤业超, 李二兵, 谭跃虎, 等. 基于能量耗散原理的盐岩动力特性及破坏特征分析[J].
岩石力学与工程学报, 2017, 36(4): 843–851.
|
| [11] |
宫凤强, 罗勇, 司雪峰, 等. 深部圆形隧洞板裂屈曲岩爆的模拟试验研究[J].
岩石力学与工程学报, 2017, 36(7): 1634–1648.
|
| [12] |
唐礼忠, 程露萍, 王春, 等. 高静载条件下受频繁动力扰动时蛇纹岩动力学特性研究[J].
岩土力学, 2016, 37(10): 2737–2745.
|
| [13] |
金解放, 李夕兵, 王观石, 等. 循环冲击载荷作用下砂岩破坏模式及其机理[J].
中南大学学报(自然科学版), 2012, 43(4): 1453–1461.
|
| [14] |
金解放, 程昀, 昌晓旭, 等. 轴向静载对红砂岩中应力波传播特性的影响试验研究[J].
岩石力学与工程学报, 2017, 36(8): 1939–1950.
|
| [15] |
刘少虹, 毛德兵, 齐庆新, 等. 动静加载下组合煤岩的应力波传播机制与能量耗散[J].
煤炭学报, 2014, 39(增刊1): 15–22.
|
| [16] |
李新平, 赵航, 罗忆, 等. 深部裂隙岩体中弹性波传播与衰减规律试验研究[J].
岩石力学与工程学报, 2015, 34(11): 2319–2326.
|
| [17] |
李新平, 董千, 刘婷婷, 等. 地应力下柱面应力波在节理岩体中传播规律研究[J].
岩石力学与工程学报, 2018, 37(增刊1): 3121–3131.
|
| [18] |
FAN LF, SUN HY. Seismic wave propagation through an in-situ stressed rock mass[J].
J Appl Geophys, 2015, 121: 13–20. DOI: 10.1016/j.jappgeo.2015.07.002. |
| [19] |
王观石, 李长洪, 胡世丽, 等. 岩体中应力波幅值随时空衰减的关系[J].
岩土力学, 2010, 31(11): 3487–3492.
DOI: 10.3969/j.issn.1000-7598.2010.11.022.
|
| [20] |
赵奎, 王更峰, 王晓军, 等. 岩石声发射Kaiser点信号频带能量分布和分形特征研究[J].
岩土力学, 2008, 29(11): 3082–3088.
DOI: 10.3969/j.issn.1000-7598.2008.11.034.
|
| [21] |
何满潮, 赵菲, 张昱, 等. 瞬时应变型岩爆模拟试验中花岗岩主频特征演化规律分析[J].
岩土力学, 2015, 36(1): 1–8.
|
| [22] |
朱权洁, 姜福兴, 于正兴, 等. 爆破震动与岩石破裂微震信号能量分布特征研究[J].
岩石力学与工程学报, 2012, 31(4): 723–730.
DOI: 10.3969/j.issn.1000-6915.2012.04.011.
|
 2018, Vol. 9
2018, Vol. 9


